Finance
Vol.3 No.2(2013), Article ID:9751,4 pages DOI:10.12677/FIN.2013.32002
Study of Liquidity Risk under HJM Framework
Department of Mathematics, Tongji University, Shanghai
Email: lixueshu@tongji.edu.cn, hendryforever@163.com
Received: Feb. 17th, 2013; revised: Mar. 8th, 2013; accepted: Mar. 27th, 2013
Copyright © 2013 Shaohua Li, Yun Tang. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT:
This paper studies the liquidity risk under the HJM framework. Through the introduction of the HJM model, we consider liquidity as a term structure and give the liquidity spread dynamic equation directly. Finally, we obtain the dynamic equation of the price of the liquidity-risk bond. Moreover, we estimate and fit the model parameters, liquidity spread and forward rate curve by the market data.
Keywords: HJM Framework; Liquidity Risk; Liquidity Spread; Statistical Fitting
HJM框架下流动性风险的研究
李少华,唐 耘
同济大学数学系,上海
Email: lixueshu@tongji.edu.cn, hendryforever@163.com
摘 要:
本文主要研究了在HJM模型框架下对流动性风险的刻画。通过对HJM模型的介绍,把流动性利差作为期限结构直接进行建模,给出流动性利差所满足的动态方程,以此推导出带有流动性风险的债券的价格。同时还通过市场数据,对模型参数、流动性利差和远期利率曲线进行了估计和拟合。
收稿日期:2013年2月17日;修回日期:2013年3月8日;录用日期:2013年3月27日
关键词:HJM框架;流动性风险;流动性利差;统计拟合
1. 引言
对于利率期限结构的研究,Health、Jarrow和Morton[1]提出了一种新的方法对固定收益证券及其衍生品进行定价,这是定价理论的一个突破。他们选择瞬时远期利率作为模拟的基本变量,用当前的收益曲线作为输入的初始条件,用瞬时远期利率满足的动态模型导出整个收益率曲线将来的随机演化过程。同时,HJM模型还一个无套利分析框架,远期利率动态过程完全由远期利率的瞬时波动率决定,因此通过对远期利率波动率期限结构的设置便可以得到不同的利率模型。HJM框架的研究具有很强的理论价值,国外对HJM模型的研究较为成熟,Cedreece Tamagushiku[2]在HJM框架下使用主成分分析对利率建模,他用了三种模型调查了悉尼期货交易所的看涨期权,三种模型都是基于HJM的框架,这三种模型分别是单因子模型,双因子模型和三因子模型,使用主成分分析的原因是为了能够提供远期利率波动函数。Chiarella和Kwon[3]系统研究了HJM模型框架下远期利率波动率的结构的一般化函数的构建,并通过对函数的设置将常见的均衡型模型纳入HJM框架下。同时HJM模型在信用风险中也有广泛的应用,Philipp J. Schonbucher[4],他使用了一种新的建模手段,假设可违约零息票债券的价格是由HJM模型驱动,从而对可违约零息票债券的定价问题进行了细致的讨论。Bielecki和Rutkowski[5],他们两个讲信用评级考虑进可违约债券的定价问题中,在HJM框架下,通过使用条件马尔科夫过程的构造来对信用级别的变动进行建模。Senay Agca[6]则侧重在HJM框架下进行风险的度量,包括传统的风险度量、通过特定的期限结构模型进行度量以及利率风险度量的实证分析。
HJM模型的框架是一般化的,不仅仅是一个利率模型,更是金融领域对期限结构建模的统一框架,在许多其他方向,如通胀率建模,信用利差建模等,都有HJM模型的身影。流动性风险亦可以用HJM框架进行建模。自从2007年金融危机以来,流动性已经成为人们越来越关注的问题,对于流动性风险的管理与控制也日趋成熟。对于流动性的定义,在一般意义上,它指的是“资金的可获得性”,即金融资产迅速变现而免遭面值损失的能力。根据国际清算银行近期一项大规模的国际比较研究,“市场流动性”指的是“市场的参与者能够迅速进行大量金融交易,并且不会导致资产价格发生显著波动”。因此,保持流动性成为金融体系健全运行的基本原则之一。目前在对流动性风险的研究中,Jarrow、Turnbull[7]和Janosi、Jarrow、Yildirim[8]提出用流动性利差来刻画流动性风险,考虑流动性风险的债券价格等于流动性贴现因子,乘以相同条件下没有流动性风险的债券价格。流动性利差指两个除了流动性不一样其余均相同的资产,其对应的收益率之差便为流动性利差。因此,流动性利差同样是一个期限结构。因此本文研究流动性风险的方法便是直接对流动性利差建模,从而完成HJM框架下流动性风险的模型建立。
2. HJM模型简介[1]
Health、Jarrow和Merton从初始市场收益率曲线出发,使用的是远期利率这一指标,得到一个完整的远期收益率曲线,建立了整个远期利率曲线动态特性的利率衍生品定价框架。
首先,固定一个时间节点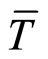 (假设为50年),对于
(假设为50年),对于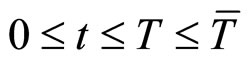 ,
,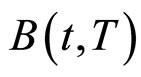 表示一个期限为
表示一个期限为![]() ,面值为1元的无风险零息票债券在
,面值为1元的无风险零息票债券在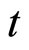 时刻的价格。那么定义在时刻
时刻的价格。那么定义在时刻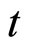 时刻适用于时刻
时刻适用于时刻![]() 投资的远期利率为:
投资的远期利率为:
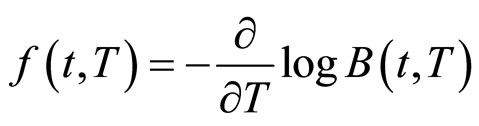 (1)
(1)
对(1)式两边积分,便可得到无风险零息票债券的价格公示:
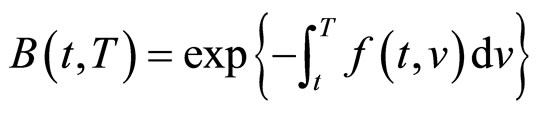 (2)
(2)
其次,假设我们已知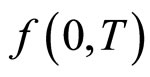 ,称为初始远期利率曲线。在HJM模型中,远期利率
,称为初始远期利率曲线。在HJM模型中,远期利率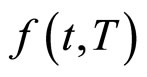 满足:
满足:
 (3)
(3)
将(3)式改写为微分的形式,即:
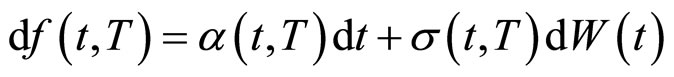 (4)
(4)
其中,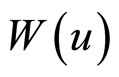 是实际概率测度
是实际概率测度![]() 下的布朗运动。
下的布朗运动。 是
是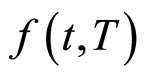 在实际概率测度下的漂移项,
在实际概率测度下的漂移项,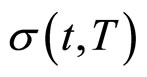 是
是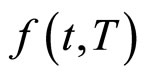 在实际概率测度下的波动项。
在实际概率测度下的波动项。
再次,进行测度转换并得到HJM模型无套利条件:即若存在随机过程 使得下式成立:
使得下式成立:
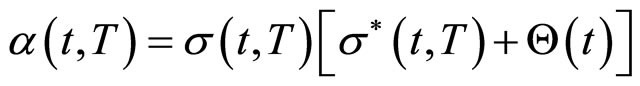 (5)
(5)
那么由单个布朗运动所驱动的关于所有到期日 的无风险零息票债券价格的期限结构模型不存在套利。其中
的无风险零息票债券价格的期限结构模型不存在套利。其中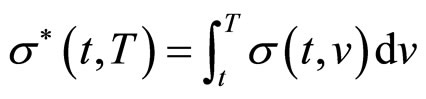 ,
, 是风险的市场价格。那么风险中性测度
是风险的市场价格。那么风险中性测度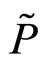 下的布朗运动满足:
下的布朗运动满足:
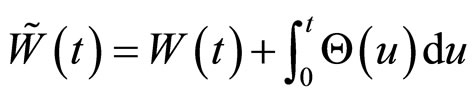 (6)
(6)
最后,得到了HJM漂移项的限制条件:
 (7)
(7)
风险中性测度下远期利率 满足的随机微分方程:
满足的随机微分方程:
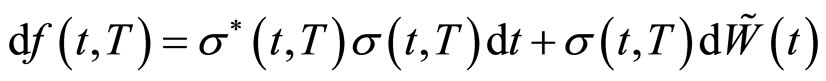 (8)
(8)
以及风险中性测度下无风险零息票债券价格 满足的随机微分方程:
满足的随机微分方程:
 (9)
(9)
由此,我们便对HJM模型简单的进行了介绍。得到了HJM漂移项限制条件、远期利率和无风险零息票债券价格满足的随机微分方程。
3. 考虑流动性风险的债券定价
我们使用流动性利差来刻画流动性风险,流动性利差便指仅流动性有差异的两个资产的收益率之差。流动性利差作为一个期限结构,我们对流动性利差直接进行建模。
首先,对于一张无风险零息票债券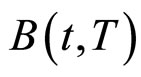 及其对应的远期利率
及其对应的远期利率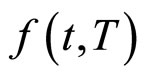 ,我们已经知道其在HJM框架下的如下的公式:
,我们已经知道其在HJM框架下的如下的公式:
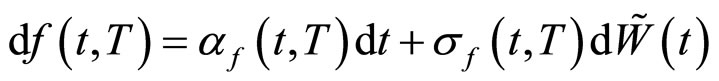 (10)
(10)
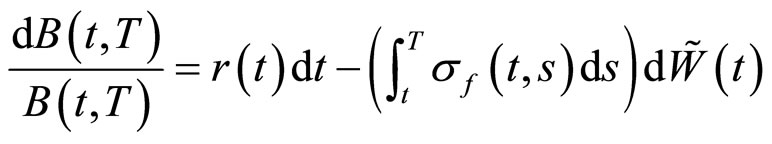 (11)
(11)
 (12)
(12)
现在考虑远期流动性利差,记为 ,假设其满足如下随机微分方程:
,假设其满足如下随机微分方程:
 (13)
(13)
对一张具有流动性风险的零息票债券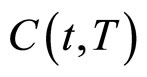 定价。因为债券具有流动性的风险,因此其价格应该等于流动性贴现因子,乘以相同条件下没有流动性风险的债券价格,即:
定价。因为债券具有流动性的风险,因此其价格应该等于流动性贴现因子,乘以相同条件下没有流动性风险的债券价格,即:
 (14)
(14)
将式(2)代入式(14):
 (15)
(15)
随后由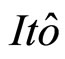 引理和式(10)、(12)可以推出
引理和式(10)、(12)可以推出
 (16)
(16)
为了研究式(16)所表示方程背后的金融含义,我们对债券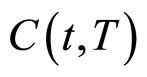 的收益率进行分析:
的收益率进行分析:
 (17)
(17)
其中 表示
表示 的收益率。同时式(16)两边也取期望,可得:
的收益率。同时式(16)两边也取期望,可得:
 (18)
(18)
式(17)与式(18)为同一个测度下同一个债券的收益率,因此两式应该相等,即:
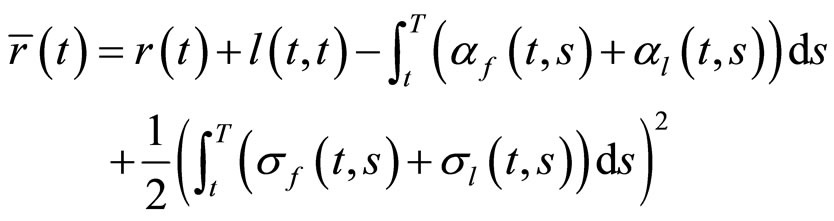 (19)
(19)
观察式(19),由流动性利差的定义,便可得:
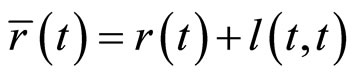 (20)
(20)
即:有流动性风险的零息票债券 的即期收益率=短期无风险利率+短期流动性利差。
的即期收益率=短期无风险利率+短期流动性利差。
再将式(20)代入式(19)中,有:
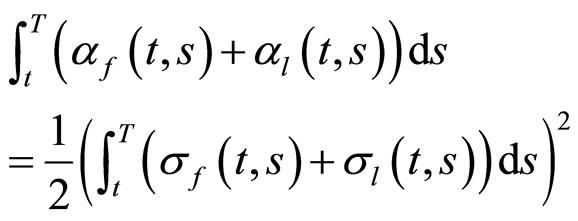 (21)
(21)
等式两边同时对![]() 求偏导,并结合式(12),可得
求偏导,并结合式(12),可得
 (22)
(22)
该式表示流动性利差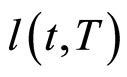 所服从的随机微分方程的漂移项限制条件。
所服从的随机微分方程的漂移项限制条件。
同时将式(21)代入(16),可得:
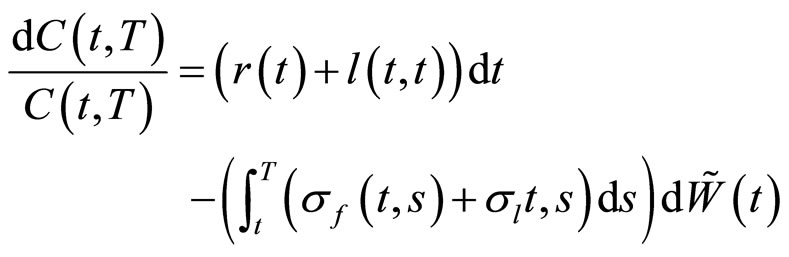 (23)
(23)
该式表示带有流动性风险的零息票债券价格所满足的随机微分方程。
至此,我们通过对远期流动性利差 直接建模,得到了HJM框架下带有流动性风险的债券价格满足的随机微分方程和远期流动性利差的随机微分方程的漂移项限制条件。
直接建模,得到了HJM框架下带有流动性风险的债券价格满足的随机微分方程和远期流动性利差的随机微分方程的漂移项限制条件。
4. 实证分析
我们用市场上的国债交易数据,对远期利率曲线、短期流动性利差、无风险零息票债券定价模型和流动性风险债券定价模型中的参数进行估计和拟合。这些参数和图像的获得,使我们对远期利率这一无法直接从市场上观测到的变量、HJM模型及其分析框架有了更直观的认识。数据源为正在交易的国债数据,时间节点为2012年10月9日,当天共计有139只国债在交易。
4.1. 零息票债权价格方程的拟合
我们已经知道HJM框架下无风险零息票债券的价格方程为(11),为了能够进行拟合,需要给予两个假设。一是,假定瞬时短期利率与时间 无关为常数,记为
无关为常数,记为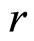 ;二是模型的波动项
;二是模型的波动项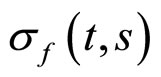 也为常数,记为
也为常数,记为 。因此,对方程(11)进行离散,得到:
。因此,对方程(11)进行离散,得到:
 (24)
(24)
其中 只是记号,表示服从标准正态分布的随机数,时间间隔为7天。
只是记号,表示服从标准正态分布的随机数,时间间隔为7天。
为了减小上述假定所造成的对参数的误差,我们对无风险零息票债券价格方程的拟合只采用一年内就将到期且在到期前不在付息的债券。
通过公式 将市场上观测到的交易价格转换为零息票价格,再根据零息票债券的特性
将市场上观测到的交易价格转换为零息票价格,再根据零息票债券的特性 得到了可以用于统计拟合输入的数据
得到了可以用于统计拟合输入的数据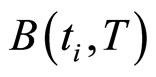 。
。
通过对随机数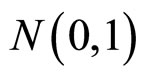 的生成,用线性回归的方法便可以拟合出
的生成,用线性回归的方法便可以拟合出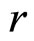 与
与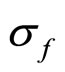 的大小。因为随机数的存在,一组数据无法真实反应待回归的参数
的大小。因为随机数的存在,一组数据无法真实反应待回归的参数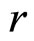 与
与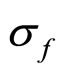 的大小,因此我们对随机数多次重复生成,每一组随机数得到一组
的大小,因此我们对随机数多次重复生成,每一组随机数得到一组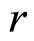 与
与 ,通过求平均数的方法来最终确定
,通过求平均数的方法来最终确定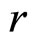 与
与 。
。
我们总共模拟了100组随机数,且每组的回归得到的模型统计量 均高于0.6,每组回归系数的
均高于0.6,每组回归系数的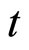 检验的显著性小于0.05,最终得到:
检验的显著性小于0.05,最终得到:
 (25)
(25)
从金融意义上来说,通过一系列零息票债券对HJM模型方程进行回归拟合,得到的短期无风险收益率为3.27%,与目前一年期存款利率3.00%相当接近;至此,我们得到了无风险零息票债券方程的参数拟合值。
4.2. 远期利率的拟合及其图像
我们已经知道HJM模型下远期利率可以用式(1)来表示,为了获得远期利率的数值,我们需要知道债券价格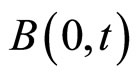 的值。根据上一节由市场数据得到的一年期
的值。根据上一节由市场数据得到的一年期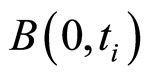 的值,我们使用多项式插值的方法来获取整个一年以内所有的
的值,我们使用多项式插值的方法来获取整个一年以内所有的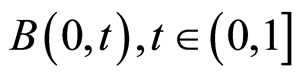 的值。
的值。
通过计算,我们最终选取三次多项式插值和二次多项式插值相结合的方法,多项式方程如下:
二次多项式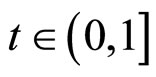 :
:
 (26)
(26)
三次多项式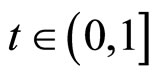 :
:
 (27)
(27)
现在对(1)式进行离散:
 (28)
(28)
利用式(26)和(27)计算每隔7天的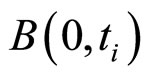 并求平均、随后用式(28)便可计算相应的
并求平均、随后用式(28)便可计算相应的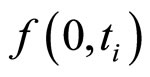 ,其像如图1:远期利率的图像符合金融上的认知,同时其值的大小也符合金融的理论。至此,我们得到了远期利率的拟合及图像s。
,其像如图1:远期利率的图像符合金融上的认知,同时其值的大小也符合金融的理论。至此,我们得到了远期利率的拟合及图像s。
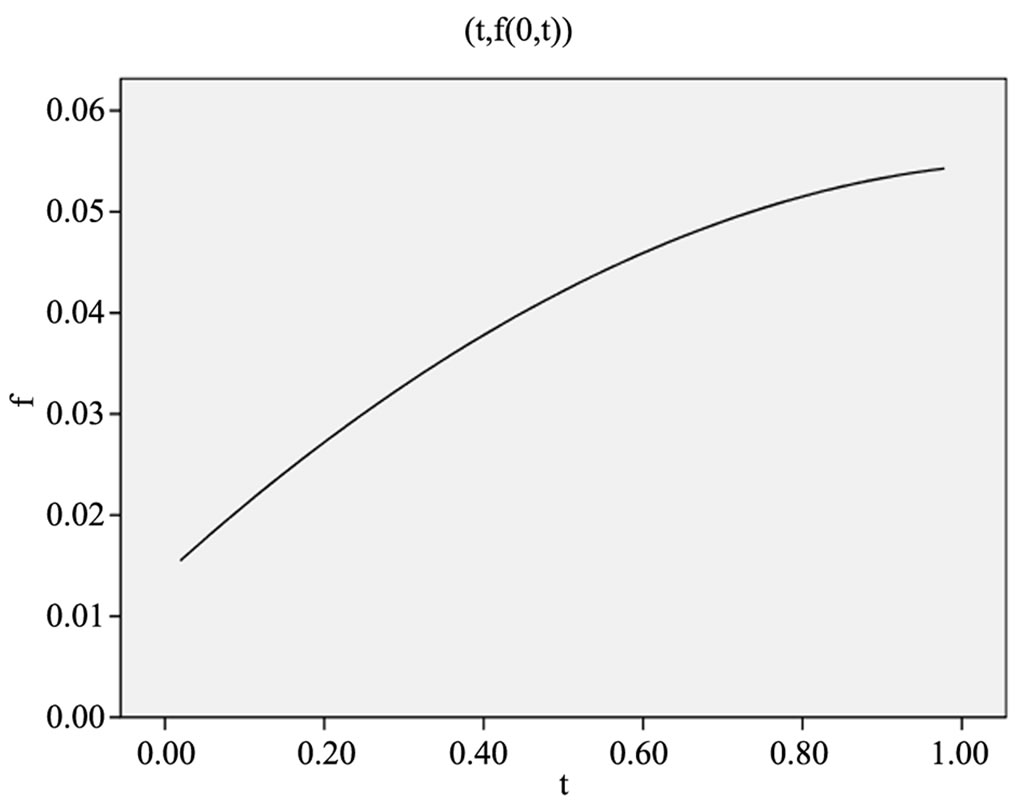
Figure 1. Curve: forward rate
图1. 远期利率曲线
4.3. 流动性风险债权价格方程的拟合与流动性利差的计算
我们已经知道流动性风险债券的价格方程为(23),与第一节拟合无风险债券的价格方程相似,为了进行拟合给出假设条件:令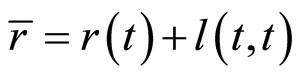 ,假设
,假设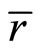 为常数,再令
为常数,再令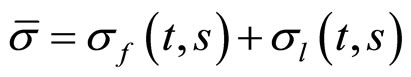 ,假设
,假设 均为常数。由此,式(23)离散为:
均为常数。由此,式(23)离散为:
 (29)
(29)
同样为了减小假定带来的误差,此处拟合只采用到期时间距时间节点1~2年的债券。
与第一节相似,通过零息票债券价格的三次与二次多项式插值方程以及付息债券的价格公式,可以得到用于统计拟合输入的数据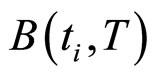 。我们也模拟了100组随机数,统计检验指标也同第一节,最终得到:
。我们也模拟了100组随机数,统计检验指标也同第一节,最终得到:
 (30)
(30)
从金融意义上来说,通过对HJM框架下带有流动性风险的债券的定价方程的拟合,得到了有流动性风险的债券的即期收益率,为5.48%。那么根据流动性利差的定义,我们便可以得到短期流动性利差的值为:
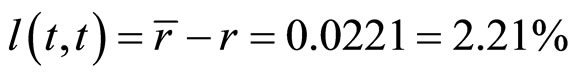 (31)
(31)
至此,我们得到了流动性风险的债券方程的参数拟合值与短期流动性利差。
5. 结论
作为期限结构建模的统一框架,HJM框架的应用越来越广。本文通过HJM框架,对流动性利差进行建模,得到了带有流动性风险的债券的定价公式以及流动性利差所满足的随机微分方程的漂移项限制条件。同时,利用市场数据对模型参数、流动性利差和远期利率曲线进行了估计和拟合,这些参数和图像的拟合,使我们对HJM框架和流动性风险有了更直观的认识。
参考文献 (References)
[1] D. Heath, R. Jarrow and A. Morton. Bond pricing and the term structure of interest rates: A new methodology for contingent claims valuation. Econometrica, 1992, 60(1): 77-105.
[2] T. Nesemann. Positive nonlinear difference equations: Some results and applications. Nonlinear Anal, 2001, 47(7): 4707-4717.
[3] C. Chiarella, O. K. Kwon. Formulation of popular interest rate models under the HJM framework. Working Paper, School of Finance and Economics, 1999: 1-20.
[4] P. J. Schonbucher. The term structure of defaultable bond prices. University of Bonn, Discussion Paper Serie B, 1996, No. 384.
[5] T. R. Bielecki, M. Rutkowski. Modelling of the defaultable term structure: Conditionally Markov approach. IEEE Transactions on Automatic Control, 2004, 49(3): 361-373.
[6] S. Agca. The performance of alternative interest rate risk measures and immunization strategies under a Heath-Jarrow-Morton framework. Virginia Polytechnic Institute and State University, 2002.
[7] R. A. Jarrow, S. M. Turnbull. The intersection of market and credit risk. Journal of Banking and Finance, 2000, 24(1-2): 271- 299.
[8] T. Janosi, R. Jarrow and Y. Yildirim. Estimating expected losses and liquidity discounts implicit debt prices. Journal of Risk, 2002, 5(1): 1-38.