Operations Research and Fuzziology
Vol.4 No.04(2014), Article ID:14180,4 pages
DOI:10.12677/ORF.2014.44007
The Relation of Two Kinds of Pointed Pseudo-Metrics on Fuzzy Lattice
1Mathematics and Statistics Institute, Henan University of Science and Technology, Luoyang
2College of Applied Science, Beijing University of Technology, Beijing
Email: chenpengbeijing@sina.com
Copyright © 2014 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received: Mar. 15th, 2014; revised: Aug. 26th, 2014; accepted Sep. 25th, 2014
Abstract
In this paper, we negative the main result that an Erceg pseudo-metric is a pointwise pseudo-metric in [1] , point out the wrong reasons in the process of its proof, and further put forward the new conclusion that a pointwise pseudo-metric is an Erceg pseudo-metric, but the converse is not true.
Keywords:Erceg Pseudo-Metric, A Pointwise Pseudo-Metric, Fuzzy Lattice

Fuzzy格上两种点式伪度量之间的关系
陈 鹏1,2
1河南科技大学,数学与统计学院,洛阳
2北京工业大学,应用数理学院,北京
Email: chenpengbeijing@sina.com
收稿日期:2014年3月15日;修回日期:2014年8月26日;录用日期:2014年9月25日

摘 要
本文否定了文[1] 的主要结果:一个点式Erceg伪度量是一个点式伪度量,并进一步给出相反的新的结论:一个点式伪度量是一个点式Erceg伪度量但反之不成立。
关键词
Erceg伪度量,点式伪度量,Fuzzy格

1. 引言
格上度量是格上拓扑学中最核心的问题,虽然迄今国内外已给出了几种较为重要的格上度量,并已取得了不少创造性工作[1] -[5] [6] ,但对它研究还远没有结束.点式度量是由史福贵教授在1996年对文[6]
中度量给出的比较合理协调的等价形式;Erceg度量是基于集合间的Hausdorff距离而被Erceg M.A.所引入[2] ,是无点化Fuzzy度量理论的优秀成果。在文[1]
中,梁基华教授给出了两者之间的一个主要结果,即该文定理1:设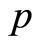 是
是 上的定式Erceg伪度量,则
上的定式Erceg伪度量,则 是一个点式伪度量。本文否决了该文的这一主要结果,指出该文错误的证明原由,并给出新的结论。
是一个点式伪度量。本文否决了该文的这一主要结果,指出该文错误的证明原由,并给出新的结论。
由于Erceg度量的定义[2] 较为复杂且直观意义不明显。鉴于此,1992年,彭育威最先给出了Erceg伪度量的点式意义的简化形式定义如下:
定义1.1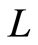 上的一个Erceg伪度量就是满足下列条件的映射
上的一个Erceg伪度量就是满足下列条件的映射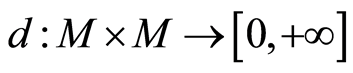 映射[3] :
映射[3] :
(B1)
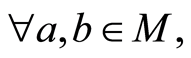 如果
如果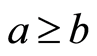 ,那么
,那么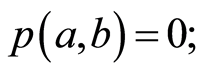
(B2)
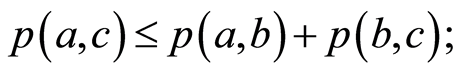
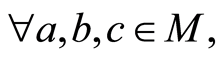
(B3)
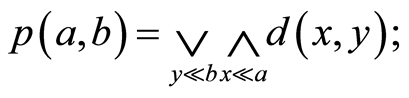
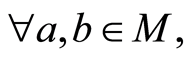
(B4)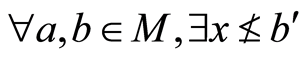 使得
使得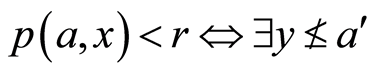 使得
使得
定义1.2 上的一个点式伪度量是一个满足下列条件的
上的一个点式伪度量是一个满足下列条件的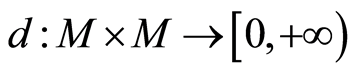 的映射[4] -[5] :
的映射[4] -[5] :
(N1)*
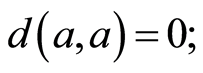
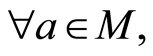
(N2)
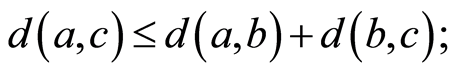
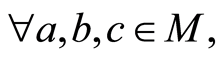
(N3)
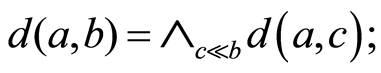
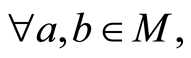
(N4)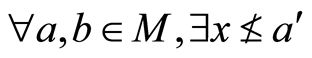 使得
使得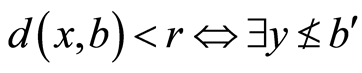 使得
使得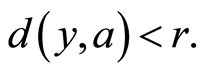
注首先(N1)*可以由下列条件
(N1)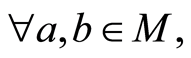 如果
如果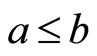 ,那么
,那么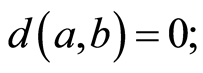
其次在史福贵定义的点式伪度量的原始定义中,还有下列条件:
(N5)*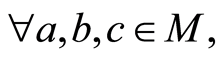 若
若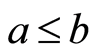 ,则
,则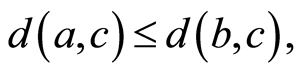
但这是多余的。事实上,当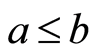 时,知
时,知 另外,(N4)能够被下面(N4)*取代,
另外,(N4)能够被下面(N4)*取代,
(N4)*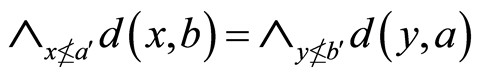
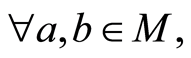 .
.
本文中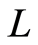 表示一个具有逆序对合对应“
表示一个具有逆序对合对应“![]() ”的完全分配格。
”的完全分配格。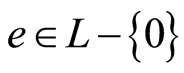 被叫一个分子,当且仅当对
被叫一个分子,当且仅当对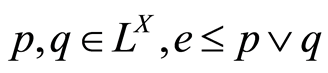 蕴含
蕴含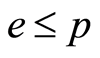 或
或 ,
,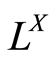 的全部分子集记为
的全部分子集记为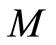 。
。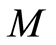 是一个连续偏序集,即
是一个连续偏序集,即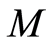 中每个元可表示
中每个元可表示 中way-below(
中way-below( )关于它的元的定向上确界[7]
。其它未声明概念与符号请参考文[8] 。
)关于它的元的定向上确界[7]
。其它未声明概念与符号请参考文[8] 。
2. 反例
文[1] 中,梁基华教授证明了:如果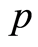 是点式Erceg伪度量,
是点式Erceg伪度量, 令
令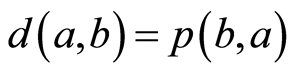 ,那么
,那么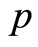 是点式伪度量,但这个结果是错误的。
是点式伪度量,但这个结果是错误的。
我们给出下面反例,它是一个点式Erceg伪度量,但不是一个点式伪度量,表明梁的这个结果是不正确。
例子2.1 设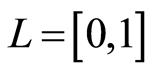 ,则,定义函数
,则,定义函数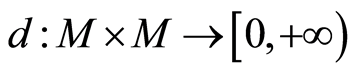 如下:
如下:
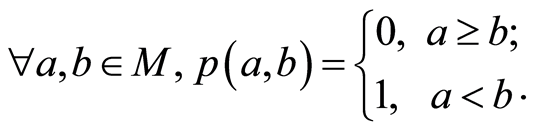
那么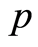 是
是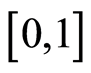 上点式Erceg伪度量。事实上,不难验证
上点式Erceg伪度量。事实上,不难验证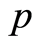 满足(B1)和(B2)。下证(B3)和(B4)。
满足(B1)和(B2)。下证(B3)和(B4)。
(B3) 如果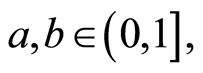 且
且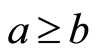 ,那么
,那么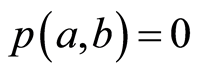 。1) 当
。1) 当 时,对每个
时,对每个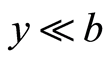 ,,即
,,即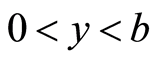 ,存在
,存在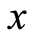 满足
满足 即
即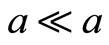 ,
,
有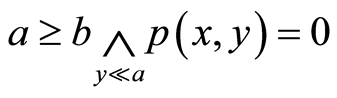 ,从而
,从而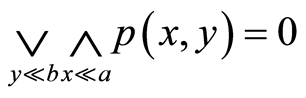 ;即有
;即有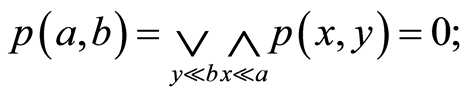 1) 当
1) 当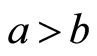 时,对每个
时,对每个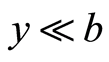 ,即
,即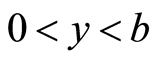 ,存在
,存在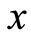 满足
满足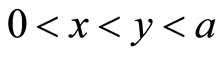 即
即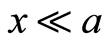 得
得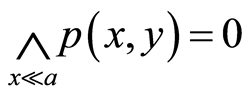 ,从而
,从而 ,即有
,即有 ;2)
当
;2)
当 时,当
时,当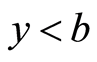 ,有分两种情况:
,有分两种情况: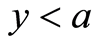 与
与 。当
。当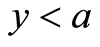 时,存在
时,存在 满足
满足 ,得
,得 ,当
,当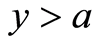 时,此时
时,此时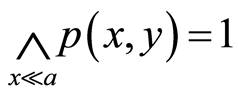 ,从而
,从而 ,即
,即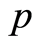 满足(B3)。
满足(B3)。
(B4) 蕴含
蕴含
蕴含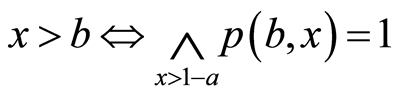 能够获得
能够获得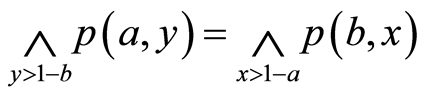 ,根据(N4)*知(B4)成立。
,根据(N4)*知(B4)成立。
但是,让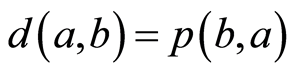 ,那么
,那么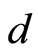 不是点式伪度量。事实上,
不是点式伪度量。事实上,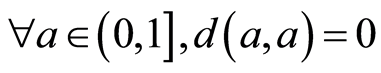 ,然而
,然而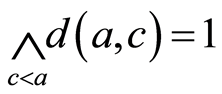 。因此
。因此 。
。
例子2.1表明,从一个彭育威意义下的点式Erceg伪度量出发,按照在文[1] 中作为定理1给出的结论是不能得到一个史福贵意义下的点式伪度量函数。
3. 本文的主要结果
定理3.1 一个映射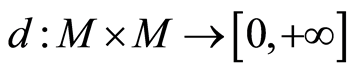 是
是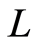 上的点式Erceg伪度量当且仅当
上的点式Erceg伪度量当且仅当 满足条件(B1),(B2),(B4)和下面(B3)*。
满足条件(B1),(B2),(B4)和下面(B3)*。
(B3)*.

证明 设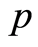 是点式Erceg伪度量,则
是点式Erceg伪度量,则 满足(B1),(B2)和(B4)。下证
满足(B1),(B2)和(B4)。下证 满足(B3)*。由于
满足(B3)*。由于
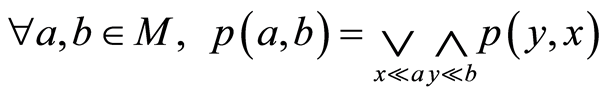 .
.
因此 ,有
,有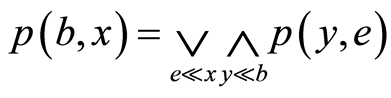 由此得
由此得
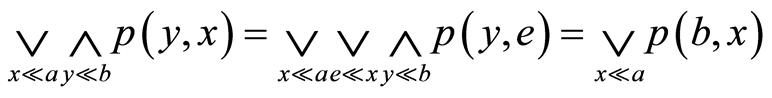 从而
从而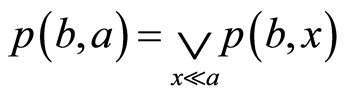 。因此
。因此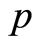 满足(B3)*。
满足(B3)*。
反之,设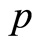 满足(B1),(B2),(B3)*和(B4)。下证
满足(B1),(B2),(B3)*和(B4)。下证 满足(B3)。
满足(B3)。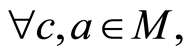 如果
如果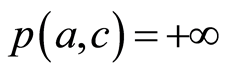 ,那么根据(B3)*,有
,那么根据(B3)*,有 。由(B1)和(B2),如果
。由(B1)和(B2),如果 ,那么我们有
,那么我们有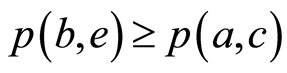 ,得
,得
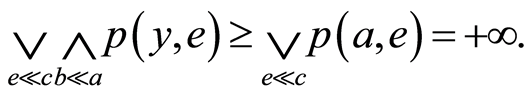
因此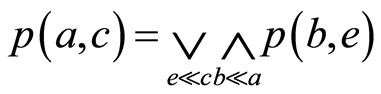 。如果
。如果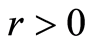 且
且 。则有
。则有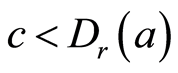 。其中定义
。其中定义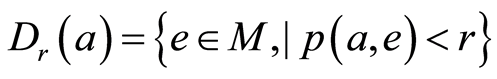 。(B4)等价于:
。(B4)等价于: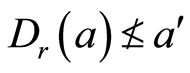
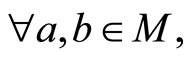 ,这是因为
,这是因为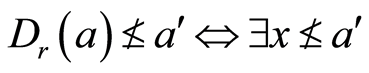 使得
使得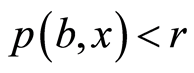 ,所以有
,所以有
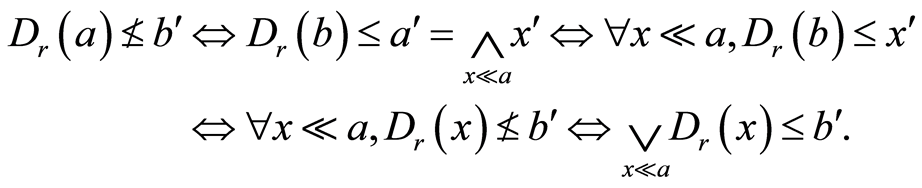
因此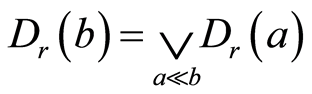 ,由此
,由此 ,存在
,存在 使得
使得 。于是
。于是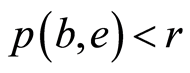 。从而有
。从而有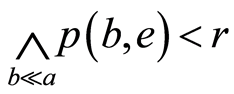 。由
。由 的任意性有
的任意性有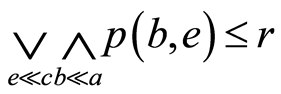 。也就是如果
。也就是如果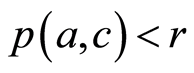 就有
就有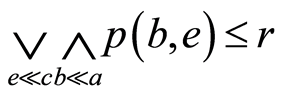 ,因此
,因此
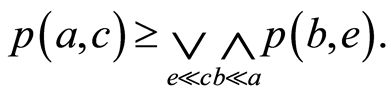
其次, ,由(B1)和(B2)得
,由(B1)和(B2)得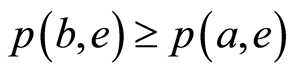 。于是
。于是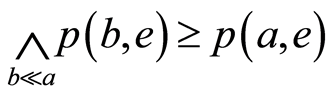 ,因
,因 满足(B3),所以
满足(B3),所以

因此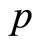 是点式Erceg伪度量。证毕。
是点式Erceg伪度量。证毕。
定理3.2 如果映射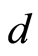 是
是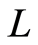 上的点式伪度量,则
上的点式伪度量,则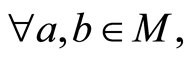 有
有
证明 满足(N1)和(N2),
满足(N1)和(N2),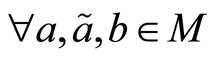 ,如果
,如果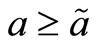 ,那么
,那么 。因为
。因为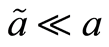 蕴含
蕴含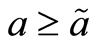 ,所以
,所以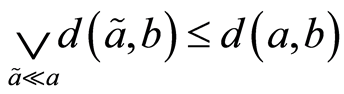 。假设
。假设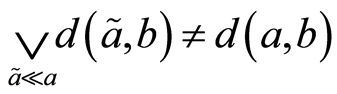 ,那么
,那么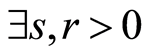 使得
使得
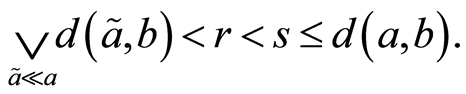
根据(N2)有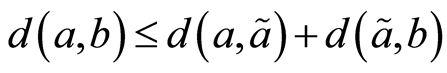 且
且 。从而
。从而
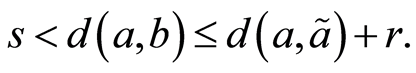
所以有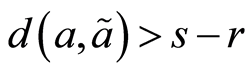 由
由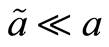 且
且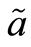 的任意性,得
的任意性,得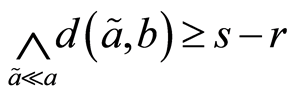 这和
这和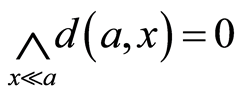 矛盾。所以
矛盾。所以
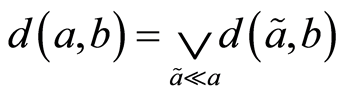 。定理被证。
。定理被证。
但从定理3.2可知,从一个点式伪度量出发,却可以容易地得到一个点式Erceg伪度量。从而,文[1] 中作为定理2的结论显然。
Erceg度量与Shi度量由于不同的连续性公理(B3)与(N3)是导致两种度量局部性质呈现出本质的差异,由于不同的连续性公理是导致Erceg度量所诱导的拓扑只能用邻域刻画,但后者的诱导拓扑用远域和邻域都能刻画。
下面例子表明Erceg伪度量诱导的拓扑一般不是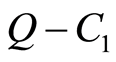 的。
的。
例3.3 设 表示第一个不可数序数,
表示第一个不可数序数,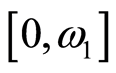 表示从0到
表示从0到 的所有序数之集。令
的所有序数之集。令
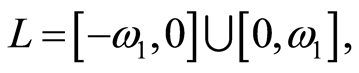
那么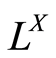 是一个具有逆序对合对应的完全分配格。再令
是一个具有逆序对合对应的完全分配格。再令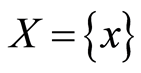 是一个单点集合。
是一个单点集合。
对每个实数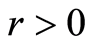 和
和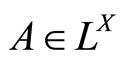 (
( 与
与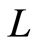 同构),规定
同构),规定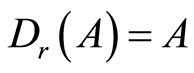 ,即
,即 是一个恒同映射,那么
是一个恒同映射,那么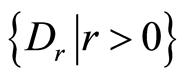 是一个Erceg伪度量的相关邻域映射族且此Erceg伪度量的拓扑是
是一个Erceg伪度量的相关邻域映射族且此Erceg伪度量的拓扑是 。取
。取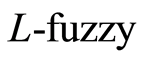 点
点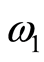 ,
,
那么 是
是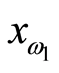 的远域族,这里
的远域族,这里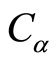 表示取值
表示取值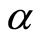 的常值
的常值 集。显然
集。显然 没有可数子集构成
没有可数子集构成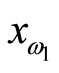 的闭远域基。因此Erceg伪度量诱导的拓扑不是
的闭远域基。因此Erceg伪度量诱导的拓扑不是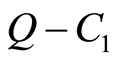 的。
的。
Erceg度量里不能直接反映格上“点式拓扑的特点”,即不能直接反映点和它的重域关系,但Shi度量却可以。
基金项目
河南科技大学博士启动项目(09001613)河南科技大学科研创新能力培育基金项目(13000810)。
参考文献 (References)
- [1] 梁基华 (2001) 关于Fuzzy格上点式伪度量的一个注记. 四川大学学报, 38, 455-498.
- [2] Erceg, M.A. (1979) Metric spaces in fuzzy set theory. Journal of Mathematical Analysis and Applications, 69, 205- 230.
- [3] Peng, Y.W. (1993) Simplification of Erceg’s fuzzy metric function and its application. Fuzzy Sets and Systems, 54, 181-189.
- [4] Shi, F.G. (1996) Pointwise quasi-uniformities and p.q. metrics on completely distributive lattices. Acta Mathematics Sinica, 5, 701-706.
- [5] Shi, F.G. (2001) Pointwise pseudo-metrics in $L$-fuzzy set theory. Fuzzy Sets and Systems, 121, 200-216.
- [6] 杨乐成 (1988) 完全分配格上的p.q.度量理论. 科学通报, 4, 247-250.
- [7] Gierz, G., et al. (1980) A compendium of continuous lattices. Springer-Verlag, New York.
- [8] Wang, G.J. (1988) Theory of $L$-fuzzy Topological Space. Shanxi Normal University Publishers, Xian.