Statistical and Application
Vol.03 No.02(2014), Article ID:13654,6
pages
10.12677/SA.2014.32006
Noncrossing Quantile Regression Modelling for Regional Education Development Data in China
Yaqi Yang, Maozai Tian*
Center for Applied Statistics, Renmin University of China, Beijing
Email: *mztian@ruc.edu.cn
Received: Mar. 5th, 2014; revised: Apr. 8th, 2014; accepted: May 19th, 2014
Copyright © 2014 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we study regional education development in China based on noncrossing quantile regression and focus on the relationship between average years of education and average GDP, education budget and teacher resources. On account of the imbalance in regional education development, quantile regression offers a complete picture of data; on the other hand, noncrossing quantile regression makes the estimators more reasonable. The results prove that economic condition hinders the development of education in low level region, while in middle level region teacher resources play a more important role, and the effects of education fund on different regions are more complex.
Keywords:Noncrossing Quantile Regression, Education Development, Quatile Differentiation

我国各地区教育发展水平的 无交叉分位回归模型
杨亚琦,田茂再*
中国人民大学应用统计科学研究中心,北京
Email: *mztian@ruc.edu.cn
收稿日期:2014年3月5日;修回日期:2014年4月8日;录用日期:2014年5月19日

摘 要
本文基于无交叉分位回归方法对我国各地区教育水平发展现状进行分析,研究了不同地区人口的平均受教育年限与人均GDP、教育经费和教师资源之间的关系。由于我国各地区教育水平发展不均衡,分位回归方法能够反映出数据的全貌,而无交叉分位回归能够使参数估计更加合理。研究结果表明,在教育水平较低的地区,教育发展受到经济条件的制约,在教育水平居中的地区,教育发展更多地受到教师资源的制约,而教育经费对不同地区的影响较为复杂。
关键词 :无交叉分位回归,教育发展水平,分位差异

1. 背景
改革开放以来,随着经济的快速发展,我国的教育水平也取得了长足的进步。但由于我国各地区经济发展极为不均衡,这也会使所谓“上层建筑”的发展水平呈现出更大差异,其中就包括教育发展水平的地区差异。教育是关系到国家长期发展的重大问题,我国也确定了教育优先发展的战略地位,因此如何提高教育发展水平,促进教育公平是值得迫切关注的问题,对于社会安定,使不同地区的人民共享发展成果具有重大意义。
近年来,很多学者对教育发展水平的区域化差异进行了系统性的研究,主要针对不同地区教育水平的评价指标、影响教育发展的因素等等。黄家泉等(2002) [1] 重点分析了区域经济差异对我国教育水平区域化差异的影响,并讨论了教育公平机制的建立。刘见芳等(2004) [2] 使用相关分析得出经济发展不平衡是我国高等教育地区差异的主要原因,地区经济和高等教育水平之间相互依存的结论。汪明(2005) [3] 介绍了义务教育均衡发展的若干保障机制,包括经费保障机制、资源共享机制、师资交流机制、生源调配机制、扶贫济弱机制和监督评价机制。刘红梅等(2013) [4] 使用了聚类分析和回归分析,从时间和空间两个角度研究了我国各地区教育发展水平的差异状况和产生原因,结果表明相对地区差异有所扩大,并发现平均受教育水平与生均预算内教育经费并不是简单的正相关关系。张海英等(2013) [5] 应用因子分析法和DEA法,从高等教育实力和效率两个方面构建综合评价矩阵,研究结果表明我国区域高等教育实力分布不均衡且效率水平总体偏低。
综合以上研究,可以看到使用的方法大多为聚类分析、因子分析和回归分析等多元统计方法,其中回归分析都基于均值回归模型,然而均值回归模型仅能反映出响应变量均值受协变量的影响,会遗漏大量信息,无法对数据进行较为全面的分析预测。分位回归可以弥补这一缺陷,针对响应变量的不同条件分位函数进行统计推断,给出数据不同层次间存在的重要信息,更全面地呈现出数据间的关系。同时,当数据中有离群点、高杠杆点存在时,分位回归比最小二乘估计更稳健,估计结果也更有效。
常规的分位回归方法常常出现不同分位回归曲线交叉的情形,也就是低分位点的估计值反而比高分位点大,这在现实中是不可能出现的。这个问题很常见,也有不少相关的研究。Koenker (1984) [6] 提出了平行分位平面的方法来避免交叉的问题,但分位平面均平行的假设显然过于严格,不符合实际情况。He (1997) [7] 假设模型为异方差回归模型,从而协变量能够通过改变分布的位置和刻度影响响应变量的分布,这在很多情况下也是不成立的。Wu & Liu (2009) [8] 提出循序地估计每个分位回归曲线,保证待估的曲线与之前的曲线不相交,这个算法的一个缺点是估计结果受估计顺序的影响。Hall et al. (1999) [9] 和Dette & Volgushev (2008) [10] 通过估计条件分布函数,再求解各分位点的方法实现了无交叉,但是这类方法只能用来估计条件分位点,但是当我们需要将协变量对响应变量的影响明确表示出来,如模型为参数模型时,就无法使用此类方法。Bondell et al. (2010) [11] 提出了同时估计不同分位函数的方法,能够估计任何样本的无交叉分位函数,并将这种方法推广到了非参数分位曲线估计。
本文结合Bondell et al. (2010) [11] 提出的方法,来分析我国教育水平的不同分位点受到人均GDP、平均每个学生享有的教育经费和学生与教师数量比值的影响,数据来自中国统计年鉴。
2. 模型及方法
假设有样本容量为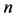 的总体分布未知的样本
的总体分布未知的样本 ,
,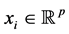 ,取协变量为
,取协变量为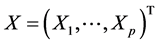 ,响应变量为
,响应变量为 ,令
,令 。我们考虑线性分位模型,即假设
。我们考虑线性分位模型,即假设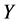 的
的 阶条件分位数为
阶条件分位数为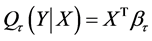 。根据Koenker & Hallock (2001) [12] ,通常我们通过下式估计
。根据Koenker & Hallock (2001) [12] ,通常我们通过下式估计 :
:
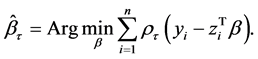 (2.1)
(2.1)
其中,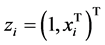 ,
,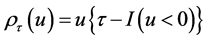 称为检验函数。式(2.1)给出的估计就是经典的分位回归估计,但无法保证分位回归曲线之间不相交。Bondell et al. (2010) [11] 提出的无交叉分位回归估计,考虑在一定限制条件下同时估计
称为检验函数。式(2.1)给出的估计就是经典的分位回归估计,但无法保证分位回归曲线之间不相交。Bondell et al. (2010) [11] 提出的无交叉分位回归估计,考虑在一定限制条件下同时估计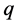 个分位点
个分位点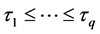 的回归曲线。协变量
的回归曲线。协变量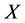 的取值范围用
的取值范围用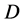 表示,假设
表示,假设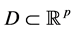 是一个凸多面体且为闭集,此时最优化问题变为
是一个凸多面体且为闭集,此时最优化问题变为
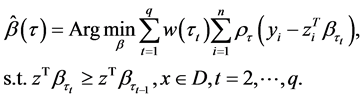 (2.2)
(2.2)
其中,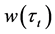 是权重函数,满足
是权重函数,满足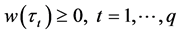 。根据Bondell et al. (2010) [11] 的定理1,在某些常规条件下,当样本量趋于无穷时,无交叉分位回归的估计结果与经典分位回归是等价的,且不受权重函数的选择的影响,也就是说权重函数的选择不影响估计结果的极限性质。因此,为简单起见,Bondell et al. (2010) [11] 选用的权重函数为
。根据Bondell et al. (2010) [11] 的定理1,在某些常规条件下,当样本量趋于无穷时,无交叉分位回归的估计结果与经典分位回归是等价的,且不受权重函数的选择的影响,也就是说权重函数的选择不影响估计结果的极限性质。因此,为简单起见,Bondell et al. (2010) [11] 选用的权重函数为 ,本文中同样使用此权重。
,本文中同样使用此权重。
当经典分位回归所得的分位曲线本来就没有交叉时,最优化问题(2.2)得出的结果与之相同。另外,假设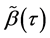 与
与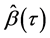 分别为无交叉的分位回归估计和经典的分位回归估计,那么如果分位点
分别为无交叉的分位回归估计和经典的分位回归估计,那么如果分位点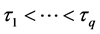 ,使得
,使得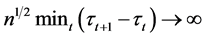 ,则
,则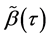 与
与 有相同的极限分布。
有相同的极限分布。
由于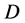 为一个凸多面体,最优化问题(2.2)的限制条件只需在
为一个凸多面体,最优化问题(2.2)的限制条件只需在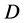 的顶点上满足即可。
的顶点上满足即可。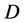 的选择可以有多种方法,比如根据经验选取或者每个解释变量的取值范围设定为样本的最大值及最小值之间等等,本文中选择
的选择可以有多种方法,比如根据经验选取或者每个解释变量的取值范围设定为样本的最大值及最小值之间等等,本文中选择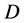 为样本所构成的凸包,在这种设定下,凸包的顶点必为样本集中的某些点,因此限制条件只需在样本集中满足即可,避免了原文中将
为样本所构成的凸包,在这种设定下,凸包的顶点必为样本集中的某些点,因此限制条件只需在样本集中满足即可,避免了原文中将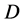 映射到
映射到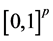 上和参数变换求解的繁复过程。这样最优化问题就变成了:
上和参数变换求解的繁复过程。这样最优化问题就变成了:
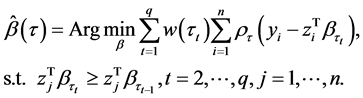 (2.3)
(2.3)
这个线性规划问题可以通过R软件包Rglpk求解。
3. 实证研究
本节中,我们使用了2004年至2011年共8年的数据来分析我国不同分位的教育水平受到协变量的
影响,选用了我国31个省份、直辖市及自治区的相关数据。响应变量和协变量的选取与调整参考刘红梅(2013),响应变量选为各地区平均受教育年限(YE),代表各地区教育水平,协变量选为生均预算内教育经费(Efund),人均GDP (AGDP),平均生师比(STR)。中国人口受教育程度分为不识字或识字很少、小学、初中、高中和大学专科及以上五个水平,对应的受教育年限分别为1、6、9、12、16年,可根据每个受教育程度人口的比例来计算平均受教育年限。计算各协变量所需的原始变量为地区预算内教育经费,地区GDP总值,地区每十万人口各级学校平均在校生数,地区每十万人口总专任教师数和地区总人口,计算方法可参考刘红梅(2013) [4] ,此处不再赘述。原始数据均来自中国统计年鉴。
下面我们展示了2004年至2011年各地区平均受教育年限的核密度函数估计,为了便于观察,2004年至2007年及2008年至2011年的密度图分别画在了图1,图2中。在2004至2007年中,核密度函数比较集中,变化并不大,都呈现出较长的左尾。在2008年至2011年中,显而易见,密度曲线有整体向右平移的趋势,说明各地区教育水平整体提高,但也可以看到受教育年限的分布仍然是不对称,每年的
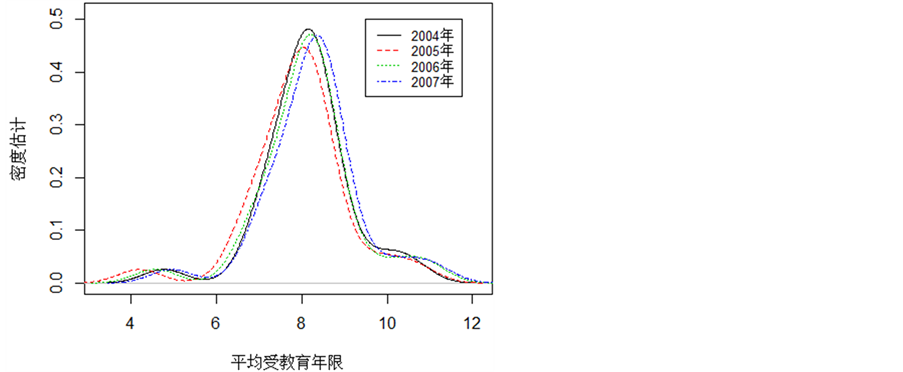
Figure 1. Density of average schooling years for different regions from 2004 to 2007
图1. 2004年至2007年各地区平均受教育年限密度图
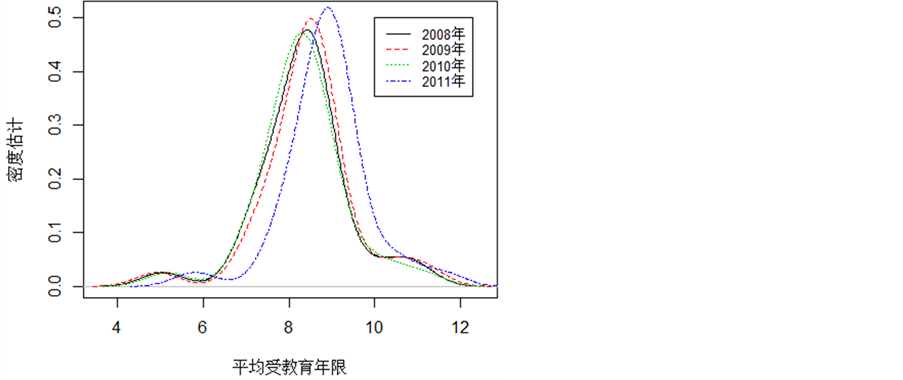
Figure 2. Density of average schooling years for different regions from 2008 to 2011
图2. 2008年至2011年各地区平均受教育年限密度图
数据都展现出左偏的特征,具有较长的左尾,说明有少数地区的教育水平很低,与平均水平差距较大。因此,为反映数据的全貌,分位回归比均值回归更有利。
分位回归分析
我们设分位回归模型为
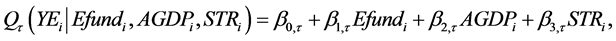
其中,分位数我们选取为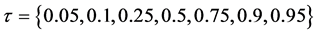 ,在经典的分位回归中,不同分位点的系数根据式(2.1)分别估计,而本文采用无交叉分位回归,根据式(2.3)同时估计,同时也使用最小二乘回归进行估计。
,在经典的分位回归中,不同分位点的系数根据式(2.1)分别估计,而本文采用无交叉分位回归,根据式(2.3)同时估计,同时也使用最小二乘回归进行估计。
在表1中,我们展示了所估的参数值。首先分析最小二乘估计的结果,可以看到人均GDP与平均教育年限是正相关的,而平均生师比和生均教育内经费与平均教育年限是负相关的。人均GDP可以影响地区的教育投入及家庭的教育投入,从而促进教育的发展,而平均生师比则反映出教育的人力投入,较低的平均生师比说明教师资源越多,故而平均生师比与平均受教育年限是负相关的。但是教育经费与平均受教育年限之间的负相关关系与我们通常的认识相左,为何会产生这个现象还需进一步分析。
我们可以利用分位回归的结果对各变量的影响做出更全面的分析,以探寻最小二乘回归无法揭示的问题。为了使结果更直观,图3中展示了各分位点参数的变化情况。首先,可以看到经典分位回归估计与无交叉分位回归估计虽然大体趋势相同,但估计值仍有一定差距,这说明使用经典分位回归已然导致了曲线的交叉,参数估计不够准确。
进一步分析各参数随分位点的变化趋势。人均GDP对于教育水平的影响是恒为正的,但是随着分位点的升高,其影响越来越小。在实际中,教育水平较高的地区往往经济水平也较高,此时,社会及家庭的教育投入已经比较高,无法获得较高的边际收益,而对于教育水平低的地区,经济水平若有提高,教育水平也能获得较多的提升。这说明在教育水平较低的地区,经济是制约其发展的一个重要因素,故促进地区经济发展,提高人民平均收入对教育有重要意义。
再观察平均生师比的系数的变化,可以发现该协变量对平均教育年限的影响恒为负,但对于极低分
Table 1. Parameter estimations under three methods
表1. 三种方法的参数估计结果
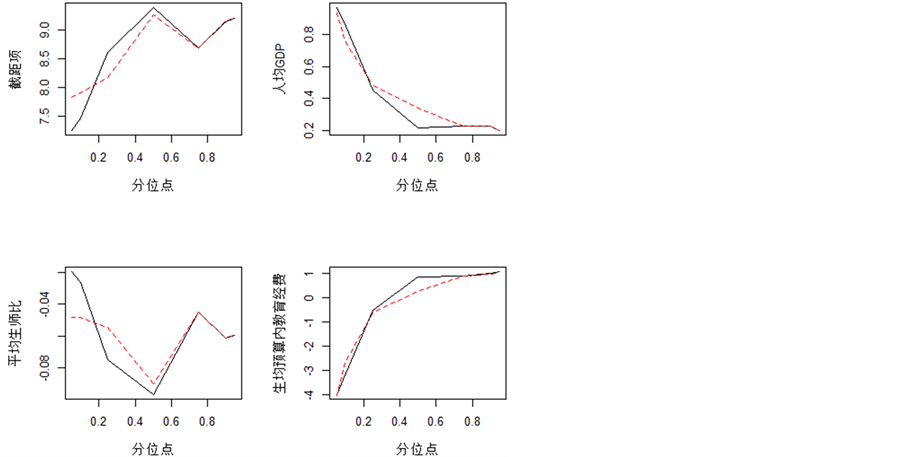 (分位回归以实线表示,无交叉分位回归以虚线表示)
(分位回归以实线表示,无交叉分位回归以虚线表示)
Figure 3. Parameter estimations under quantile regression and noncrossing quantile regression (Solid lines result from quantile regression and dashed lines result from noncrossing quantile regression)
图3. 分位回归及无交叉分位回归参数估计结果(分位回归以实线表示,无交叉分位回归以虚线表示)
位点和较高分位点其影响较小,而对0.25分位点和0.5分位点其影响较大。说明在教育水平处于较低或中间水平的地区,教育水平受平均生师比的影响较大,教育水平的进一步提升很可能受到了教师资源短缺的制约。因此,提高人力投入,对教育水平较低或处于中间位置的地区尤其重要。
最后,生均预算内教育经费的系数随分位数的变化也体现出明显的趋势,当分位点提高时,其系数也随之提高,在0.5分位点处由负值变为正值,0.95分位点的系数与0.05分位点系数的差达到1.078 ‒ (‒4.026) = 5.104了。这个现象的产生大概来自两方面的原因:一方面,国家为扶持教育落后地区教育水平的发展,会增加其教育投入,因此这个系数在一定程度上包含着一个反方向的因果关系;另一方面,教育经费如果未能得到有效合理利用,那么增加教育经费投入也不能真正提高教育水平。
4. 结论与建议
近年来,我国教育水平从整体上来说已获得了很大的提高,但教育发展不平衡的现象却一直存在。在教育水平落后地区及教育发达地区,教育发展受各方面因素的影响也是不同的。为了找到经济水平、教师资源和经费投入对不同层次教育水平发展的影响,我们采用了无交叉分位回归的方法。
我们得到的主要结论有:第一,经济水平的提高对不同地区的教育水平提高均有正面的影响,但教育越落后的地区,经济水平的影响越明显;第二,教师资源对教育水平处于中等的地区影响最大;第三,生均预算内教育经费对教育水平较高的地区有正面的影响,但对教育落后的地区却有负面的影响。
针对以上得到的结论及文中对原因的分析,我们提出以下几点建议:
第一,促进教育落后地区的经济发展,提高当地居民的收入,使人民有余力资金用在孩子的教育上,另一方面可以对贫困地区学生提供补助,以此避免一些学生因经济条件不足而无法继续学业;
第二,对教育水平处于中等的地区,要加大教师资源的投入,号召更多的优秀教师到教师资源短缺的地区就职,并提高相应待遇和优惠条件以吸引人才;
第三,在教育水平落后的地区,教育经费的使用应该更科学地安排。对于教育落后的地区,国家应该加强对其教育经费使用情况的监督,并促使其向教育水平高的地区学习发展教育的经验。如果一味地加大教育投入,而无法科学地使用,就不能得到应有的教育产出,只会造成浪费,充分合理地利用教育经费才具有更深远的意义。
综上所述,我国教育水平的提高需要因地制宜,对于不同教育发展水平的地区采取不同的措施,以促进教育水平的全面发展,缩小地区间的教育水平差异。在教育相对落后的地区,应从多方面入手弥补差距,尤其要解决教育发展中的“短板问题”,使人力、物力的投入能够更大效率地发挥协同作用。
致谢
本文获得下面基金部分资助:国家自然科学基金(No. 11271368),北京市哲学社会科学规划项目(No. 12JGB051),教育部高等学校博士学科点专项科研基金(No. 20130004110007),国家社会科学基金重点项目(No. 13AZD064),全国统计科研计划项目(No. 2011LZ031)以及兰州商学院“飞天学者特聘计划”。
文章引用
杨亚琦,田茂再, (2014) 我国各地区教育发展水平的无交叉分位回归模型
Noncrossing Quantile Regression Modelling for Regional Education Development Data in China. 统计学与应用,02,37-43. doi: 10.12677/SA.2014.32006
参考文献 (References)
- 1. 黄家泉 (2002) 教育区域化发展研究:地区经济发展不平衡对教育的影响. 山西人民出版社, 太原.
- 2. 刘见芳 (2004) 我国高等教育发展水平地区差异研究. 硕士论文, 清华大学, 北京.
- 3. 汪明 (2005) 义务教育均衡发展与若干保障机制——部分地区的政策及实践分析. 教育发展研究, 10, 40-44.
- 4. 刘红梅 (2013) 中国各地区教育发展水平差异的实证研究. 数理统计与管理, 4, 586-594.
- 5. 张海英 (2013) 我国区域高等教育水平的综合评价. 统计与决策, 1, 66-67.
- 6. Koenker, R. (1984) A note on L-estimators for linear models. Statistics and Probability Letters, 2, 323-325.
- 7. He, X. (1997) Quantile curves without crossing. The American Statistician, 51, 186-192.
- 8. Wu, Y. and Liu, Y. (2009) Stepwise multiple quantile regression estimation using non-crossing con-straints. Statistics and Its Interface, 2, 299-310.
- 9. Hall, P., Wolff, R.C.L. and Yao, Q. (1999) Methods for estimating a conditional distribution function. Journal of the American Statistical Association, 94, 154-163.
- 10. Dette, H. and Volgushev, S. (2008) Non-crossing non-parametric estimates of quantile curves. Journal of the Royal Statistical Society, 70, 609-627.
- 11. Bondell, H.D., Reich, B.J. and Wang, H. (2010) Non-crossing quantile regression curve estimation. Biometrika, 97, 825-838.
- 12. Koenker, R. and Hallock, K. (2001) Quantile regression. Journal of Economic Perspective, 15, 143-156.
