Advances in Applied Mathematics
Vol.05 No.01(2016), Article ID:16493,7
pages
10.12677/AAM.2016.51001
Linear Complementarity Problems under a Random Symmetric Uncertainty
Dan Wu1, Jiye Han2
1School of Mathematics and Statistics, Henan University of Science and Technology, Luoyang Henan
2Institute of Applied Mathematics, Chinese Academy of Sciences, Beijing

Received: Nov. 16th, 2015; accepted: Dec. 6th, 2015; published: Dec. 9th, 2015
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we introduce the notion of robust solution of uncertain linear complementarity problems. We prove that, if robust counterpart to uncertain quadratic programming—a robust optimization problem, has a optimal solution , and the optimum value equals to zero, then
, and the optimum value equals to zero, then 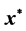 is the robust solution of the uncertain linear complementarity problem. By probability theory, we discuss linear complementarity problems under a random symmetric uncertainty, and obtain sufficient and necessary conditions of almost reliable robust solution.
is the robust solution of the uncertain linear complementarity problem. By probability theory, we discuss linear complementarity problems under a random symmetric uncertainty, and obtain sufficient and necessary conditions of almost reliable robust solution.
Keywords:Uncertain Linear Complementarity Problems, Robust Solution, A Random Symmetric Uncertainty

随机对称不确定集下的线性互补问题
吴 丹1,韩继业2
1河南科技大学,数学与统计学院,河南 洛阳
2中国科学院应用数学研究所,北京

收稿日期:2015年11月16日;录用日期:2015年12月6日;发布日期:2015年12月9日

摘 要
本文引入不确定线性互补问题鲁棒解的概念。而且,我们证明:如果不确定二次规划问题的robust Counterpart,这一鲁棒优化问题的存在最优解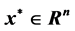 ,并且最优值为0,那么
,并且最优值为0,那么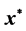 就是不确定线性互补问题的鲁棒解。我们讨论当不确定集为随机对称分布时,线性互补问题的求解。借助于概率论知识,给出
就是不确定线性互补问题的鲁棒解。我们讨论当不确定集为随机对称分布时,线性互补问题的求解。借助于概率论知识,给出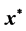 为almost reliable鲁棒解的充要条件。
为almost reliable鲁棒解的充要条件。
关键词 :不确定线性互补问题,鲁棒解,随机对称不确定集

1. 引言
20世纪下半页以来,优化技术在自然科学、工程技术、经济管理、交通规划、网络设计等各个领域得到了广泛的应用。数学规划的经典范例是在输入数据准确知道并且等于某些额定值的假设条件下建立模型,并利用已有的数学规划方法求解模型得出最优解。然而,这种方法并没有考虑数据不确定性对模型的质量和可行性的影响[1] -[3] 。事实上,数据的不确定性是无处不在的。数据的不确定性会对优化问题的最优解和最优值造成一定的影响,那么这种影响是否会导致传统模型的解失去意义呢?Ben-Tal等人在中给了一个生产药品的线性优化问题实例,在该实例中,2%的数据扰动会使得最优值下降超过10%,这也说明在固定参数值后得到的最优解在这数据扰动下远远脱离可行性。类似地,Ben-Tal和Nemirovski曾对NETLIB线性规划问题库中的90个问题进行了数值实验,结果表明,0.01%数据扰动会使这90个问题当中的13个问题的最优解可行性遭到严重的破坏: 经过0.01%的数据变动后,最初的最优解不能满足某些约束,并且会超出这些约束的边界值50%甚至更多。这些实例说明,有些时候即使很小的数据扰动也会对优化问题带来较大的影响[4] -[7] 。本文以不确定线性互补问题为研究对象,借助于概率论知识,给出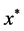 为almost reliable鲁棒解的充要条件。
为almost reliable鲁棒解的充要条件。
2. 不确定线性互补问题
本文采用鲁棒优化技术研究不确定线性互补问题。首先,对于不确定线性互补问题:
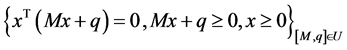 (1)
(1)
给出鲁棒解的定义。
定义2.1令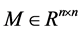 是一个
是一个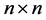 实矩阵,
实矩阵, 是一个
是一个 维向量,
维向量,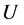 是一个不确定集,寻求
是一个不确定集,寻求 ,满足:
,满足:
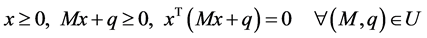 (2)
(2)
称上述问题的解为不确定线性互补问题的解。即若问题(2)的解存在,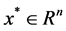 ,则对任一
,则对任一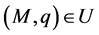 ,式子
,式子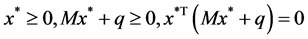 均成立。
均成立。
显然,不确定线性互补问题已转化为对一系列,无数个线性互补问题的求解。对于这样的模型,像投影法、内点法、非光滑牛顿法以及光滑牛顿法等,这些常用的方法将不再适用。因此,我们的首要任务就是将这样一种未知的带有不确定集的线性互补问题转化为已知的拥有高效处理技术的最优化问题,甚至是互补问题来求解。
我们知道,对于线性互补问题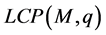 的求解可以借助于二次规划问题:
的求解可以借助于二次规划问题:
(QP): 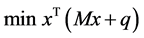
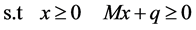 (3)
(3)
其中 。
。
如果二次规划问题有解 ,并且最优值为0,即
,并且最优值为0,即 ,那么最优解
,那么最优解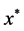 就是线性互补问题
就是线性互补问题 的解。
的解。
当 为不确定输入数据元素,只知道它们属于某一不确定集合
为不确定输入数据元素,只知道它们属于某一不确定集合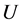 时,我们可得不确定二次规划问题:
时,我们可得不确定二次规划问题:
 (4)
(4)
根据鲁棒优化理论,定义问题(2)的robust counterpart (RC)。
定义2.2 确定一个不确定元素集合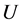 ,我们称问题:
,我们称问题:
(RC) 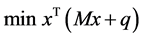
 (5)
(5)
其中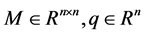 为不确定二次规划问题的robust counterpart.称该问题的最优解
为不确定二次规划问题的robust counterpart.称该问题的最优解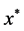 为不确定二次规划问题的鲁棒最优解。
为不确定二次规划问题的鲁棒最优解。
定理2.1 如果上述鲁棒优化问题(RC)的最优解存在 并且最优值为0,则
并且最优值为0,则 是不确定线性互补问题的鲁棒解。
是不确定线性互补问题的鲁棒解。
3. 随机对称不确定集下的线性互补问题
定义3.1 不确定集 的随机对称是指:不确定元素的真实值
的随机对称是指:不确定元素的真实值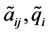 是由其额定值
是由其额定值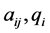 的随机对称扰动而获得的。
的随机对称扰动而获得的。
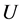 可以表示成:
可以表示成:
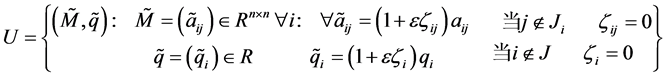 .
.
其中,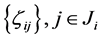 是
是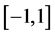 上对称分布的相互独立的随机变量。
上对称分布的相互独立的随机变量。
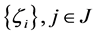 是
是 上对称分布的相互独立的随机变量,
上对称分布的相互独立的随机变量, 为不确定水平。
为不确定水平。
如果问题含有随机变量,对于不确定线性互补问题解的理解,从以往对不等式确定性的满足转变为概率意义下的满足是十分必要的。特别是条件:
对于任一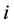 事件
事件
 和
和
 即
即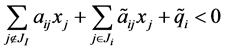 (6)
(6)
的概率至多是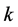 ,
,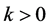 为给定的可靠水平。
为给定的可靠水平。
定义 3.2:我们称满足条件(3)的解为不确定线性互补问题的almost reliable解。
令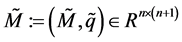 ,
, (7)
(7)
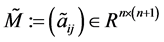 ,
,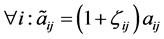 当
当 时,
时, 。
。
其中,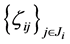 是
是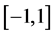 上的相互独立的对称分布的随机变量。其中,
上的相互独立的对称分布的随机变量。其中,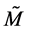 的第
的第 列就是向量
列就是向量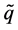 ,
, ,
,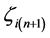 就是由
就是由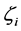 转化而来。
转化而来。
那么,对于随机对称分布不确定集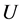 ,问题(RC)就转化为:
,问题(RC)就转化为:
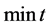
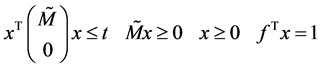 (8)
(8)
其中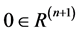 ,
, 。
。
下面,我们将以问题(8)为模型,研究带有随机对称不确定集的线性互补问题。首先,给出如下著名结论。
引理3.1:设 为给定的实数,
为给定的实数, 为
为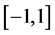 上对称分布的独立的随机变量。那么对于任意
上对称分布的独立的随机变量。那么对于任意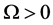 ,有
,有
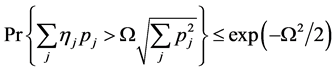 (9)
(9)
利用上述引理,我们可得,当不确定集为随机对称分布时,线性互补问题的almost reliable鲁棒解的充要条件。
定理3.1:如果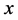 可以扩展为以下不等式组的解
可以扩展为以下不等式组的解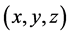 ,
,
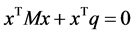

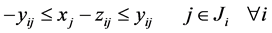 (10)
(10)
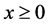
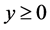
其中 为一正系数。
为一正系数。
那么,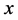 是不确定线性互补问题的almost reliable解,可靠水平
是不确定线性互补问题的almost reliable解,可靠水平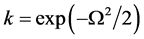 。
。
证明 首先证明:如果 可以扩展为以下优化问题的可行解
可以扩展为以下优化问题的可行解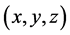 ,
,
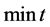

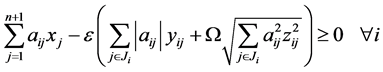 (11)
(11)
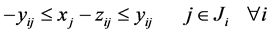


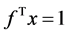
其中 为一正系数。
为一正系数。
那么对于问题(8),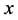 违反约束条件的概率至多为
违反约束条件的概率至多为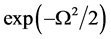 。
。
设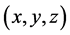 为(2.29)的可行解,首先考虑
为(2.29)的可行解,首先考虑 违反约束条件
违反约束条件 的概率:
的概率:

有引理3.1可知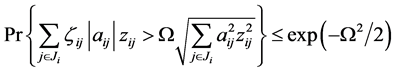
同理,可得约束条件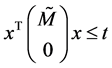 的违反概率。
的违反概率。
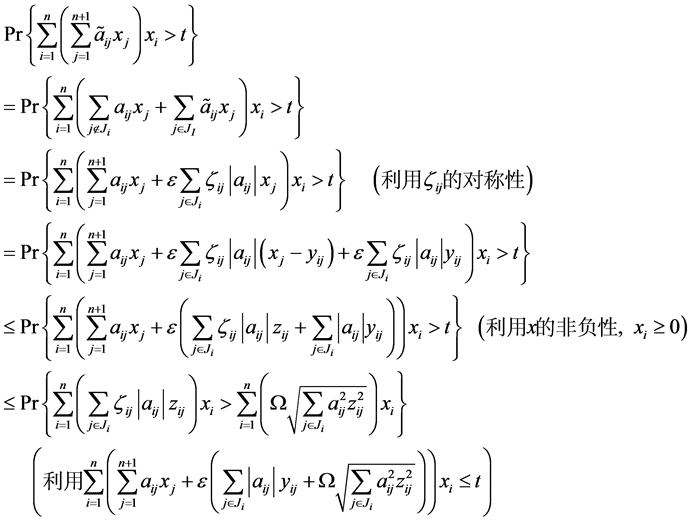
由于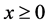 ,不妨设事件A:
,不妨设事件A:
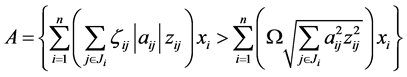
事件B: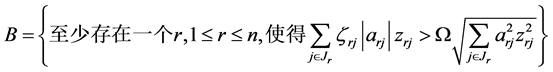
由
所以,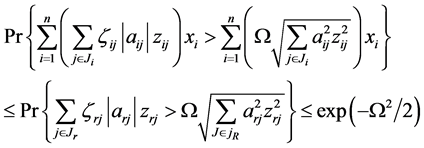
综上所述,对于问题(8),由(10)得到的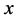 ,违反约束条件的概率至多为
,违反约束条件的概率至多为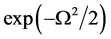 。
。
由定理2.1和定义3.2可推得,如果存在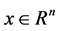 可以扩展为下述不等式组的解
可以扩展为下述不等式组的解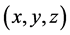 ,
,

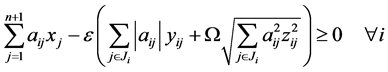 (12)
(12)
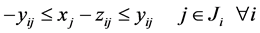
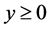
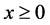
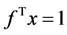
则 是不确定线性互补问题的almost reliable解,可靠水平为
是不确定线性互补问题的almost reliable解,可靠水平为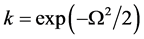 。
。
假设 满足(12)条件②~⑥,则可推得
满足(12)条件②~⑥,则可推得

从而条件①为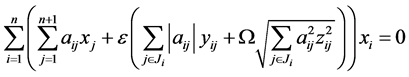 ,也就是
,也就是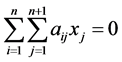 ,并且
,并且 。
。
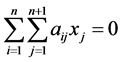 ,由
,由 ,以及
,以及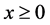 ,
,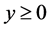 ,可得
,可得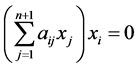
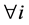 。
。
若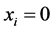 ,当然有
,当然有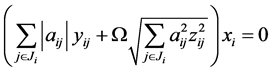 。
。
若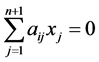 ,由
,由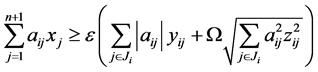 可得
可得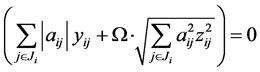 ,即
,即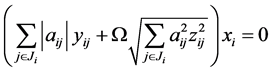 。
。
所以,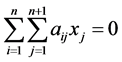 可推得
可推得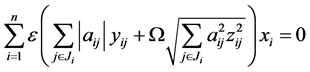 。再由(12),就等价于
。再由(12),就等价于
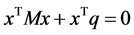
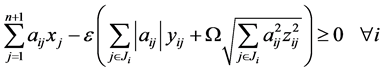
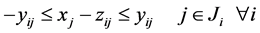

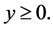
特别是,当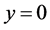 ,(10)就转化为
,(10)就转化为
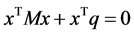
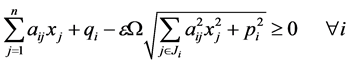 (13)
(13)

基金项目
国家自然科学基金资助项目(11426091, 11471102)。
文章引用
吴丹,韩继业. 随机对称不确定集下的线性互补问题
Linear Complementarity Problems under a Random Symmetric Uncertainty[J]. 应用数学进展, 2016, 05(01): 1-7. http://dx.doi.org/10.12677/AAM.2016.51001
参考文献 (References)
- 1. Ben-Tal. A. and Nemirovski. A. (1997) Stable Truss Topology Design via Semidefinite Programming. SIAM Journal on Optimization, 7, 991-1016. http://dx.doi.org/10.1137/S1052623495291951
- 2. Ben-Tal, A. and Nemirovski, A. (1998) Robust Convex Optimization. Mathematics of Operations Research, 23, 769- 805. http://dx.doi.org/10.1287/moor.23.4.769
- 3. Ben-Tal, A. and Nemirovski, A. (2000) Robust Solutions of Linear Programming Problems Contaminated with Uncertain Data. Mathematical Programming, 88, 411-424. http://dx.doi.org/10.1007/PL00011380
- 4. Ben-Tal, A., El-Ghaoui, L. and Nemirovski, A. (2000) Robust Semi-definite Programming. Kluwer Dordrecht.
- 5. Fang, H., Chen, X. and Fukushima, M. (2007) Stochastic Matrix Linear Complementarity Problems. SIAM Journal on Optimization, 18, 482-506. http://dx.doi.org/10.1137/050630805
- 6. Ferris, M.C. and Pang, J.S. (2010) Engineering and Economic Appli-cations of Complementarity Problems. SIAM Review, 39-69.
- 7. Goldfarb, D. and Iyengar, G. (2010) Robust Portfolio Selection Problems. Mathematics of Operations Research, 28, 1-37. http://dx.doi.org/10.1287/moor.28.1.1.14260