ABSTRACT

In this paper, the asymptotic behavior of the initial value problem for the singularly perturbed first order nonlinear differential equation with a degenerate equation having roots of multiplicity two is studied. With the purpose of obtaining a more precise description of the boundary layer, the modified method of boundary layer function is applied to construct the boundary layer function possessing the behavior of exponential decay characteristic and then the asymptotic solution is constructed and used to prove that the formal asymptotic solution is uniformly valid.

Keywords:Singularly Perturbed Initial Value Problem, Multiple Root, Exponentially Decaying Boundary Layer, Asymptotic Expansion, Uniformly Valid

退化方程具有重根的奇摄动初值问题解的渐近分析

张蕊蕊，陈松林^*，马文冉

安徽工业大学数理科学与工程学院，安徽 马鞍山

收稿日期：2016年12月19日；录用日期：2017年1月9日；发布日期：2017年1月16日

摘 要

本文研究退化方程具有重根的奇摄动一阶非线性微分方程初值问题的渐近解的构造。为了获得更为精细的边界层刻画，本文采用修正的边界层函数法，得到具有指数衰减渐近特性的边界层函数。利用所获得的形式渐近解去构造上下解，证得该形式渐近解的一致有效性。

关键词 :奇异摄动初值问题，重根，指数衰减边界层，渐近展开，一致有效性

1. 引言

对于初值问题

(1)

(2)

其中是正的小参数，与是连续可微函数。

由文献 [1] 可知，若初值问题(1)，(2)的退化方程

有单根，且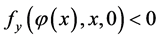, 那么问题(1)，(2)存在唯一解，且有一致有效的渐近展开式

其中是由初值问题

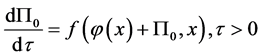
所定义的边界层函数，且知估计

(，是与无关的正数)

进一步，若函数充分光滑，那么，对于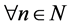，都可获得解带有估计的一致有效渐近展开表示式。

对于退化方程具有多个单根时的奇异摄动初值问题，已有较为深入的讨论 [2] [3] 。但对退化方程具有重根时的奇异摄动问题，由于保证渐近解的渐近稳定性条件一般并不满足，相关研究较少。KW Chang, FA Howes就此情形进行了讨论，在吉洪诺夫稳定性条件下得到了一致有效的边界层型解，文献 [4] [5] [6] 中

已经讨论了，其退化方程有二重根的情况，但所得到的边界层函数是按幂律衰减的，渐

近误差估计的阶较低。

本文将研究初值问题(1)，(2)在是退化方程的重根时解的渐近分析，且将获得具有指数衰减渐近特性的边界层函数，改进了已有的结果 [7] 。

以下就二重根的情形进行讨论。为了后面的讨论，作以下假设

A1：函数具有形式

(3)

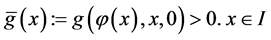
其中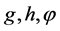，是充分光滑的函数。

2. 问题渐近解的构造

假设A1成立，我们采用经典的合成法求问题(1)，(2)形如

(2.1)

的形式渐近解，其中，是正则项，是边界层项，为伸长变量。

把(2.1)代入(1)，再利用表达式

假设

(2.2)

(2.3)

把正则项按级数展开

(2.4)

把(2.4)和(3)代入(2.2)得

(2.5)

比较同次幂系数，得

(2.6)

(2.7)

其中

假设A2：设在上，方程(2.7)有两个实根，且。

由韦达定理可知，所以可得出。

进一步，我们还可以推出以下关系式

(2.8)

考虑，可得方程

(2.9)

类似地，我们还可以求出

再设边界层项具有按的形式级数展开

(2.10)

把(2.10)，(2.4)，(3)代入(2.3)，得

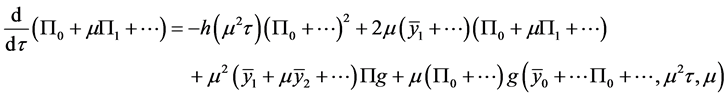(2.11)

由(2)，(2.1)，(2.4)，(2.10)可知

(2.12)

比较的同次幂系数，得

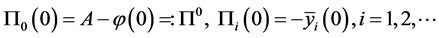(2.13)

按照改进的边界层函数构造法, 由(2.11)和(2.13)可得函数满足下述初值问题

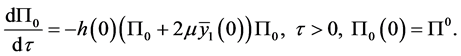(2.14)

得

(2.15)

假设A3：。

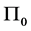再由A2易知，且对于任意的，当时，满足：

。即具有指数衰减特性。

继续使用上述方法，由(2.11)，(2.13)我们构造关于的初值问题

(2.16)

其中, 且有估计

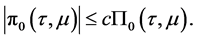
解得

(2.17)

假若我们将表示成

。 (2.18)

则可以得出估计

(2.19)

由此可以看出估计增加了项。然而，其将不利于后面上、下解的构造，因此我们将对方法再次改进，并尝试在构造时增加项，此时新获得的关于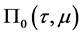的初值问题为

(2.20)

考虑到关系式：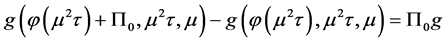

所以问题(2.20)可以写成如下形式

(2.21)

其中

记(2.21)的解为

(2.22)

并可得出估计

对关于边界层函数的奇摄动初值问题

(2.23)

。

其中

解得

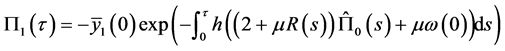(2.24)

比较(2.22)和(2.24)，得

类似地，关于边界层函数的奇摄动初值问题

(2.25)

其中

解得

(2.26)

易得估计

类似地，我们还可以求出

并证得其满足的估计

3. 证明渐近解的有效性

定义初值问题(1)，(2)的形式渐近解为

(3.1)

利用此函数构造初值问题(1)，(2)的上、下解，继而得出其一致有效性。

引理：假设在上，存在函数，如果函数在区域D：

上连续，且当时，满足不等式

则对任意满足的常数A，初值问题

在区间上总有一个解，并成立不等式

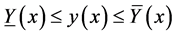
此时称， 为初值问题的下、上解。

定理：假设A1-A3成立，那么对于充分小的，初值问题(1)，(2)存在解，且有一致有效的渐近估计：

其中

证明：构造

(3.2)

其中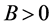，后面确定。

再由(2)得：

另有

将关于和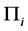的方程代入上述表达式，经计算得

(3.3)

由已知条件A1，A2可知，，且，故适当选取B可得不等

式

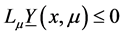(3.4)

即为初值问题(1)，(2)的下解。

类似地，可以证明函数

(3.5)

在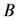充分大时，是初值问题(1)，(2)的上解。

至此由引理我们便得出，初值问题(1)，(2)必存在解满足：

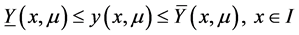
再由(3.2)，(3.5)可得出

。

类似地，对更大的自然数k，我们可获得更高阶在上一致有效的渐近表示式。

例：考虑奇摄动初值问题

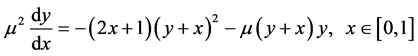
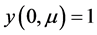
其中

，，，

。

解得正则部分

。

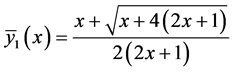边界层部分：

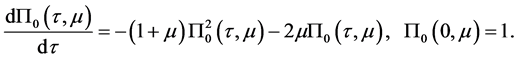
解得

。

。

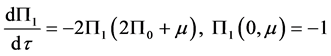解得

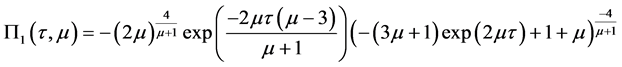
因此，问题的解可以表示成

致谢

感谢导师、审稿老师以及编辑老师的指导和提出的宝贵意见。

基金项目

研究生创新研究基金(20141031)；安徽省高校自然科学研究重点项目(KJ2016A084)。

文章引用

张蕊蕊,陈松林,马文冉. 退化方程具有重根的奇摄动初值问题解的渐近分析
Asymptotic Analysis for the Singularly Perturbed Initial Value Problem with Degenerate Equation Having Multiple Root[J]. 应用数学进展, 2017, 06(01): 1-9. http://dx.doi.org/10.12677/AAM.2017.61001

参考文献 (References)