Advances in Applied Mathematics
Vol.06 No.02(2017), Article ID:19923,9
pages
10.12677/AAM.2017.62012
Stability and Bifurcation of Mechanical System with Parameters in Damping Optimization Problem
Ruijie Jin
School of Mathematics, Lanzhou Jiaotong University, Lanzhou Gansu

Received: Feb. 27th, 2017; accepted: Mar. 18th, 2017; published: Mar. 21st, 2017

ABSTRACT
The paper discusses the dynamical behavior of mechanical system containing parameter with damping optimization, and studies the stability and Hopf bifurcation of the system by using quasi- nonintegrable Hamilton system theory. Then, the conditions of local and global stability of system obtain the largest Lyapunov exponent boundary and category. Next, we solve stationary probability density function and jointly stationary probability density function by using FPK equation. Finally, we illustrate the result of bifurcation by parametric variation.
Keywords:Random Parameters, Random Excitation, Stochastic Stability, Hopf Bifurcation
含参数的机械系统在阻尼优化问题中的稳定性与分岔分析
金瑞婕
兰州交通大学数理学院,甘肃 兰州
收稿日期:2017年2月27日;录用日期:2017年3月18日;发布日期:2017年3月21日

摘 要
本文讨论了含参数的机械系统在阻尼优化问题中的动力学行为。通过拟不可积的哈密顿理论来研究它的稳定性及Hopf分岔问题,再通过最大Lyapunov指数理论和边界种类来分析它的局部稳定性和全局稳定性。根据解决得到的FPK方程得到平稳概率密度函数和联合概率密度函数,进行数值模拟,最后说明参数变化对分岔的影响。
关键词 :随机参数,随机激励,随机稳定性,Hopf分岔

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
从十九世纪末起,人们开始对非线性动力学问题多研究,由于像杜芬这样伟大的物理学家和力学家通过对一些相关实验的研究成果,于是促进了分岔、混沌理论体系及非线性科学的形成和发展 [1] 。近年来,很多学者运用非线性的思维来解决一些问题。王洪礼通过对硅藻和甲藻的研究,建立相关的非线性动力学模型,然后运用拟不可积的Hamilton相关理论和乘积遍历法,求得最大Lapunov指数,得到稳定性的条件并且讨论系统进行分岔时的条件 [2] 。
在机械系统的阻尼优化问题中,它的动力学行为受到的外激励中有很多种因素,因此根据随机非线性动力学理论来研究含有参数的机械系统的阻尼优化问题中的动力学特性是非常有必要的。
近些年来,已经将非线性随机动力学与控制的研究转向Hamilton体系 [3] 。文章提供了一种研究Hamilton系统的hopf分岔的方法,分析了在随机参数激励下系统的随机局部稳定性和随机全局稳定性,利用随机平均法得出一维扩散过程的边界和联合概率密度及平稳概率密度的图像的特点,得出hopf分岔的条件,进行数值仿真,探讨了参数变化时对系统Hopf分岔的影响 [4] 。
2. 系统模型
在外加激励,阻尼很小的情况下,系统会出现分岔、混沌等复杂的动力学现象。在含参数的机械系统的阻尼优化问题中 [5] ,这个系统可以用常微分方程表示如下:
 (1)
(1)
 是质量,
是质量, 是刚度矩阵,阻尼矩阵
是刚度矩阵,阻尼矩阵 是取决于阻尼位置的半正定矩阵,参数
是取决于阻尼位置的半正定矩阵,参数 被称为粘度,
被称为粘度,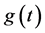 是所受的外力。
是所受的外力。
确定性系统是在理想状态下的,但实际上我们无法忽略随机因素给研究动力学行为带来的影响。由于外激励和内部随机振荡的原因, 是均值为零的高斯白噪声。
是均值为零的高斯白噪声。
 (2)
(2)
令
 (3)
(3)
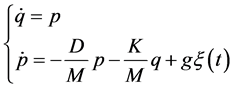 (4)
(4)
根据方程(2)可以写成相应的无阻尼自治系统:
 (5)
(5)
忽略高阶小量对能量的影响,可求得Hamilton函数
 (6)
(6)
根据拟不可积的Hamilton系统理论,这个拟不可积的Hamilton方程弱依概率弱收敛于一维ITO扩散过程,关于Hamilton方程的平均ITO方程可以写成:
 (7)
(7)
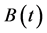 是标准维纳过程,
是标准维纳过程, 和
和 是分别是伊藤随机过程的漂移和扩散系数,
是分别是伊藤随机过程的漂移和扩散系数, 是积分区域,由拟不可积的Hamilton系统的随机平均法可求得
是积分区域,由拟不可积的Hamilton系统的随机平均法可求得 和
和 :
:
由
 (8)
(8)
解得

由
 (9)
(9)
解得
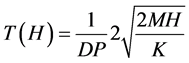
由
 (10)
(10)
解得

由
 (11)
(11)
解得

3. 随机稳定性
3.1. 局部稳定性
一般通过系统的最大李雅普诺夫指数来研究系统的稳定性,由Oseledec乘积遍历性定理可判定局部稳定性。
ITO随机微分方程的最大李雅普诺夫指数为:(7)式的平凡解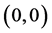 是唯一的,在
是唯一的,在 处将其线性化,得到伊藤微分方程为:
处将其线性化,得到伊藤微分方程为:
 (12)
(12)
则
 (13)
(13)
由线性化系统的最大Lyaponov指数定义 [6] 得
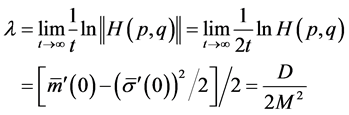 (14)
(14)
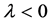 ,即
,即 ,伊藤方程的平凡解以概率1渐进稳定,能量稳定在一个固定值。
,伊藤方程的平凡解以概率1渐进稳定,能量稳定在一个固定值。
 ,即
,即 在随机激励下发生失稳现象。
在随机激励下发生失稳现象。
 ,即
,即 发生分岔。
发生分岔。
3.2. 全局稳定性
运用Lyapuonv指数来判断稳定性具有一定的局限性。常用奇异边界理论来分析系统的全局稳定性。ITO方程的边界类别由当 时的左边界和
时的左边界和 时的右边界是奇异边界主要的两个性态。
时的右边界是奇异边界主要的两个性态。
当 时,使得
时,使得 ,即属于第一边界分类。漂移扩散系数分别收敛到(15)和(16)式
,即属于第一边界分类。漂移扩散系数分别收敛到(15)和(16)式
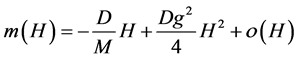 (15)
(15)
 (16)
(16)
 为左漂移指数和左扩散指数及特征标值,可得
为左漂移指数和左扩散指数及特征标值,可得
 (17)
(17)
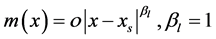 (18)
(18)
 (19)
(19)
所以边界是属于排斥自然的。
当 时,
时, ,即属于第二边界分类。
,即属于第二边界分类。
可知

漂移扩散指数及特征标值为:

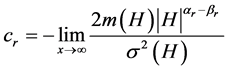 (20)
(20)
其中, 为右漂移指数和右扩散指数及特征标值。
为右漂移指数和右扩散指数及特征标值。
可知 ,
,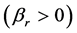 ,
, ,
,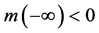 或
或 ,所以属于越出边界。
,所以属于越出边界。
4. 随机分岔
随机分岔理论是指随着参数的改变使得动力系统的定性性态也发生变化(即改变系统的拓扑结构)的研究,一般可分为D分岔和P分岔。D分岔点用Lyapunov指数的正负来判定。P分岔根据随机动力系统的平稳概率密度函数图像随参数的改变发生变化的研究 [7] 。
当特征标值 时,系统在某个能量值处能出现最大概率密度,也就是该系统在受到随机参数激励的时候可能出现的能量大小,当参数发生变化时,系统可能会发生Hopf分岔,产生极限环,震荡变剧烈,最终或许导致破坏,通过求解FPK方程来确定该模型产生Hopf分岔的条件。
时,系统在某个能量值处能出现最大概率密度,也就是该系统在受到随机参数激励的时候可能出现的能量大小,当参数发生变化时,系统可能会发生Hopf分岔,产生极限环,震荡变剧烈,最终或许导致破坏,通过求解FPK方程来确定该模型产生Hopf分岔的条件。
对应的FPK方程
 (21)
(21)
 (22)
(22)
这里, 是平稳概率密度函数。
是平稳概率密度函数。
将 带入
带入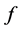 得到:
得到:
 (23)
(23)
这里,A是归一化常数。
可以得出
 (24)
(24)
最终可以得到联合概率密度函数
 (25)
(25)
当 ,
, 是一个
是一个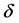 函数;当
函数;当 时,
时, 是一个减函数,并且在原点处取得最大值,此时出现第一次分岔;当
是一个减函数,并且在原点处取得最大值,此时出现第一次分岔;当 时,
时, 依然取得最大值,但是最大值位置远离原点,并且发生第二次分岔。
依然取得最大值,但是最大值位置远离原点,并且发生第二次分岔。 ,发生动态分岔;
,发生动态分岔;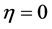 ,发生唯像分岔。这两次分岔构成了随机Hopf分岔。
,发生唯像分岔。这两次分岔构成了随机Hopf分岔。
5. 数值仿真
由于参数众多,本文选取对控制系统全局稳定性有主要意义的A为分岔控制参数。
设其他参数为 。
。
我们主要讨论系统在 处的Hopf分岔,可以得到当参数取A是的平稳概率密度和联合概率密度。图1~6是参数取不同变化值时的平稳概率密度和联合概率密度图像,平稳概率密度图像中,随着参数的变化,图像由单调函数,逐渐变为单峰图像,对应的联合概率密度图像逐渐出现火山口,可判断在发生分岔的条件。随着参数的变化,最大值远离远点,说明分岔点向右移动,平稳概率密度的最大值减小,也说明了发生分岔的概率减小。
处的Hopf分岔,可以得到当参数取A是的平稳概率密度和联合概率密度。图1~6是参数取不同变化值时的平稳概率密度和联合概率密度图像,平稳概率密度图像中,随着参数的变化,图像由单调函数,逐渐变为单峰图像,对应的联合概率密度图像逐渐出现火山口,可判断在发生分岔的条件。随着参数的变化,最大值远离远点,说明分岔点向右移动,平稳概率密度的最大值减小,也说明了发生分岔的概率减小。

Figure 1. The phase diagram of stationary probability density and bi- furcation position when 
图1. 当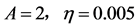 时平稳概率密度f的相图和分岔位置
时平稳概率密度f的相图和分岔位置

Figure 2. The phase diagram of stationary probability density and bi- furcation position when 
图2. 当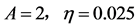 时平稳概率密度f的相图和分岔位置
时平稳概率密度f的相图和分岔位置

Figure 3. The phase diagram of stationary probability density and bifurcation position when 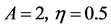
图3. 当 时平稳概率密度f的相图和分岔位置
时平稳概率密度f的相图和分岔位置

Figure 4. Jointly stationary probability density when A = 2, η = 0.05
图4. 选取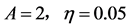 时联合概率密度图
时联合概率密度图
从图1到图3的数值模拟可知,当参数增大时,系统的平稳概率密度图形也发生变化。随着参数的变化,图像由单调函数,逐渐变为单峰图像。
从图4到图6能够得出随着参数的变小,它的联合概率密度图像也发生了一些变化,由单峰变成火山口,取值越小,火山口的形状也越明显。

Figure 5. Jointly stationary probability density when A = 2, η = 0
图5. 选取 时联合概率密度图
时联合概率密度图

Figure 6. Jointly stationary probability density when A = 2, η = 0.5
图6. 选取 时联合概率密度图
时联合概率密度图
6. 结论
本文考虑了随机激励对系统的影响,根据非线性动力学理论,将其转化为高斯白噪声。根据拟不可积的哈密顿理论和Oseledec乘积遍历法的相关知识,为研究含有随机激励系统的稳定性和分岔特性提供了一种分析方法。了解到最大李雅普诺夫指数来判定稳定性的局限性,用一维扩散过程的边界分类理论来分析全局稳定性,得到发生分岔的条件。最后,通过运用matlab和maple来进行数值模拟。本文提供的方法其现实意义在于,当系统稳定性条件被破坏之后,为建立可靠函数和首次穿越的问题提供了可靠的理论根据。
我们在实际问题的研究中,要合理的控制参数,避免出现随机分岔,不要对我们的正常工作和生活带来不好的影响,这才是我们做的真正有意义的事。
文章引用
金瑞婕. 含参数的机械系统在阻尼优化问题中的稳定性与分岔分析
Stability and Bifurcation of Mechanical System with Parameters in Damping Optimization Problem[J]. 应用数学进展, 2017, 06(02): 105-113. http://dx.doi.org/10.12677/AAM.2017.62012
参考文献 (References)
- 1. 徐伟. 非线性随机动力学的若干数值方法及研究[M]. 北京: 科学出版社, 2013: 1-60.
- 2. 王洪礼, 许佳, 葛根. 赤潮藻类非线性动力学模型的随机分岔[J]. 海洋通报, 2008, 27(2): 37-42.
- 3. 朱位秋. 非线性随机动力学与控制[M]. 北京: 科学出版社, 2003: 1-341.
- 4. 葛根, 王洪礼, 许佳. 矩形薄板在面内随机参数激励下的随机分岔研究[J]. 振动与冲击, 2011, 30(9): 253-258.
- 5. Kuzmanović, I., Tomljanović, Z. and Truhar, N. (2016) Damping Optimization over the Arbitrary Time of the Excited Mechanical System. Journal of Computational and Applied Mathematics, 304, 120-129. https://doi.org/10.1016/j.cam.2016.03.005
- 6. 王洪礼, 许佳, 葛根. 机翼震颤的随机Hopf分岔研究[J]. 机械强度, 2008, 30(3): 368-370.
- 7. 魏星. 载流矩形薄板在磁场中的随机分岔[D]: [硕士学位论文]. 秦皇岛: 燕山大学, 2016.