Biophysics
Vol.2 No.1(2014), Article ID:13734,12 pages
DOI:10.12677/BIPHY.2014.21001
Cellular Automata Modeling of HIV-Immune System
Department of Physics, School of Physics and Mechanical & Electrical Engineering, Xiamen University, Xiamen
Email: *jianweishuai@xmu.edu.cn
Copyright © 2014 Youbin Mo et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for Hans and the owner of the intellectual property Youbin Mo et al. All Copyright © 2014 are guarded by law and by Hans as a guardian.



Received: Jan. 12th, 2014; revised: Jan. 27th, 2014; accepted: Feb. 2nd, 2014
ABSTRACT
It is more than 30 years since the first case of Acquired Immune Deficiency Syndrome (AIDS) has been reported. However, we still cannot find the effective treatment though this terrible sickness kills approximately two million patients per year. Using mathematical model for approaching the dynamics of human immunodeficiency virus (HIV) infection was and still is one of most important methods among the numerous studies of the treatments of AIDS. Constructing a correct mathematical model of HIV infection will help us to investigate the interaction between HIV and immune and shed light on AIDS treatment. In this article, we review the recent development of cellular automata model to discuss the interaction mechanism between HIV and immune cells, and the drug treatment.
Keywords: HIV; AIDS; Cellular Automata

HIV感染–免疫动力学的元胞自动机模拟研究
莫有斌,林 海,帅建伟*
厦门大学物理与机电工程学院物理系,厦门
Email: *jianweishuai@xmu.edu.cn
收稿日期:2014年1月12日;修回日期:2014年1月27日;录用日期:2014年2月2日

摘 要
自1981年发现首例人类获得性免疫缺失综合症(艾滋病,AIDS)至今已有30多年,然而人们至今未能找到治疗这种危及人类生命健康的可怕疾病的方法。建立正确的艾滋病病毒HIV与免疫系统相互作用数学模型,有助于发现HIV的感染机理,帮助我们找到治疗AIDS的方法。在这篇报告中,我们综述了利用元胞自动机模型来揭示HIV与免疫系统相互作用的研究,包括模拟HIV感染后病人出现三个典型的特征期(急性期、潜伏期和AIDS发病期)的动力学过程,以及对应的药物治疗理论研究。
关键词
HIV;AIDS;元胞自动机

1. 前言
1981年6月5日,美国疾病控制与预防中心通报了首例获得性免疫缺陷综合征(Acquired Immunodeficiency Syndrome)(AIDS)病例,揭开了人类与艾滋病的抗争历史[1]。人类免疫缺陷病毒(Human Immunodeficiency Virus, HIV)于1983年被发现[2],1984年研究证实HIV是引起AIDS的病原体[3,4]。三十年来,艾滋病在全球范围内以惊人的速度传播,成了现代历史上最严重的瘟疫,迄今为止,已有三千万人死于艾滋病及其并发症[5]。单在2005年,全世界范围内就有大约3800万人受到HIV的感染,其中大约410万人是新增病例,280万人死于艾滋病[6,7]。而在中国,每年新增病例大约5万人,因艾滋病死亡约2万人[8]。
自从AIDS出现以来,人们就致力于研究其发病机理和治疗方案[9,10]。其中何大一博士在1995年提出的高效抗逆转录病毒治疗(Higgly Active Anti-Retroviral Therapy, HAART)方案,获得了很大的成功。但该疗法仍未能完全清除HIV携带者体内的病毒[11-13]。近年来有不少艾滋病治疗方法提出,包括药物治疗法、免疫治疗法、基因治疗法等[14-18],但至今未有任何一种疗法能够彻底治愈艾滋病。与此同时,对HIV感染动力学的理论研究也日渐取得进展。但人类现有的认识不足以找到彻底消灭AIDS疾病的方法。人们仍然在对抗艾滋病这条道路上不断努力。对AIDS的最终攻克,一方面依赖于实验技术的改进和医学科技的发展;另一方面也依赖于在更加全面深刻地认识AIDS的发病机理的基础上,建立合理的理论模型进行计算和模拟,进而寻找有效的治疗药物、设计有效的治疗手段。
病人在被HIV感染后,会出现三个典型的特征期:急性期、潜伏期和AIDS发病期[19](图1)。被HIV感染后的1~8周内,病人体内的CD4+T细胞数量急剧减少,随后回升,HIV浓度急剧上升后回落到非常低的水平,这个时期称为急性期,也叫做初次感染期。随后的2~10年里,病人体内的HIV浓度会稳定在非常低浓度的水平,这个时期称为潜伏期。处于潜伏期的病人从外表上看跟正常人没有任何区别,因此该时期也叫无症状期。根据临床数据,在没有进行治疗的情况下,潜伏期会持续2~8年。在潜伏期结束的时候,病人体内病毒数会在某个时刻迅速增长,并且CD4+T细胞数量下降到正常水平的30%以下,这时候病人进入了AIDS发病期。在AIDS发病的时候,病人会因为免疫系统受破坏、变异的癌细胞无法及时清除以及其他抗原入侵而死亡。
至今为止,人们对HIV感染并致发病的动力学原理已进行了大量的研究。HIV病毒是一种逆转录RNA病毒。它由两条RNA链、RNA逆转录酶以及包裹它的类脂结构包膜组成。包膜上嵌入的gp120糖蛋白与CD4+T细胞有很高的亲和力,因此,HIV病毒的主要攻击对象是免疫系统中的CD4+T细胞。HIV病毒与CD4+T细胞结合后,会把核内的RNA、逆转录酶等释放到宿主细胞中。逆转录酶会利用宿主细胞中的原

Figure 1. The clinic data of time evolution of CD4-T cells and HIV for HIV infected patients
图1. HIV感染后病人体内细胞/HIV病毒的数量随时间变化的临床测量数据
料使RNA反转录成cDNA。cDNA在宿主细胞合成蛋白时,转录出自己的mRNA并翻译成病毒蛋白。这些病毒蛋白与病毒RNA一起组装成新的HIV病毒。当宿主细胞内的HIV病毒数超过一定阈值时,这些新病毒就会破坏宿主细胞的细胞膜,以出芽的形式离开宿主细胞。宿主细胞因为细胞膜受到破坏,膜通透性提高而裂解死亡。被HIV病毒感染的CD4+T细胞还有另一种死亡方式,也即是被CD8+T细胞识别并激活了它的凋亡程序。无论是哪一种原因,处于被感染末期的CD4+T细胞都会很快死亡。
健康人的免疫系统会以一定的速率补充和更新死亡的CD4+T细胞,以维持免疫系统的活性。如果免疫系统的CD4+T细胞数量能够维持在正常的水平,那么HIV携带者会保持在潜伏期,而不会进入AIDS发病期。HIV携带者之所以会从潜伏期发展到AIDS发病期,现在学界普遍的认识是:HIV病毒的高突变率导致免疫系统识别新病毒能力跟不上新病毒的变异速率,因此导致免疫系统瘫痪,引起了AIDS发作。
HIV病毒的遗传物质是RNA,由于缺少DNA双链的校正机制,因此它在复制的时候有很高的几率发生突变。同时,因为免疫细胞CD4+T细胞和B细胞具有抗原特异性,所以在新的HIV病毒种株产生的时候,免疫系统需要重新识别新HIV病毒的蛋白特性,以产生新的免疫球蛋白。在免疫系统识别新HIV病毒的时候,寄生在宿主细胞中的HIV病毒可能已经变异出了若干代新HIV病毒种株。于是乎免疫系统又需要重新识别抗原特性。在上述的过程中,免疫系统识别HIV病毒的步伐永远落后于HIV病毒变异速率。这个抗衡的最终的结果就是HIV病毒变异出大量免疫系统无法识别的HIV病毒种株,使得人体特异性免疫系统被彻底破坏。
建立艾滋病的数学模型,给研究人员提供一种可靠的模拟方法来定量研究艾滋病机理和治疗等[20-26]。针对HIV病人出现的三个典型特征期,HIV感染的三阶段动力学模型大致分为如下几种类型:一种是最通常的微分方程模型[27-33];也有提出在离散空间的蒙特卡罗随机模型[34,35];另一种是元胞自动机(Cellular Automata)模型[36-40]。
本文主要针对元胞自动机模型进行综述。Weisbuch和Atlan与1988年首先提出用元胞自动机研究病毒-免疫系统的研究[36],随后Dayan和Pandey等对该模型进行了研究[37-39]。Dos Santos和Coutinho在2001年提出了一个HIV元胞自动机模型(HIV-元胞自动机模型)[40],他们在该模型中建立了一个二维的矩形网格阵列,并假设每一个网格有4种可能的状态(健康态、感染-A态、感染-B态、死亡态)。通过给定这4种状态之间的4条演变规则、参数取值和初始条件,该模型能够模拟出HIV感染之后的出现的三种状态-急性期、潜伏期和发病期。由于该模型能很好的模拟HIV的一些基本特征,该模型的提出极大地刺激了HIV元胞自动机的研究。本文第二章为元胞自动机模型概述及原理介绍,第三章综述元胞自动机模拟HIV-免疫系统相互作用动力学过程,第四章综述元胞自动机模拟药物治疗在HIV-免疫系统中的作用,第五章讲述HIV元胞自动机的数学方程描述,最后为总结和展望。
2. 元胞自动机
2.1. 元胞自动机概述
元胞自动机(Cellular Automata,简写为元胞机),也叫细胞自动机、格状自动机(早期文献也用tessellation automata,homogeneous structures,cellular structures,tessellation structures,iterative arrays等名称),是一种时间和空间变量都取离散值的动力系统理想化模型[41-44]。由于它的时间空间变量是离散值,物理参量只取有限值,所以在计算机技术飞速发展的二十世纪九十年代受到各领域研究仿真模拟的研究人员追捧[45,46]。
作为建造仿真模拟动力学过程模型的基础,元胞自动机具有以下几大优点:1) 元胞自动机模拟的对象是一些独立的、边界特征明显、空间分布上具有一定规律的个体,如晶格、组织中的细胞、生物个体等。元胞自动机的时空离散性特征使得它在处理离散对象时,转化规则简单明了。同时,还可以对元胞自动机进行一系列数学分析和求解。2) 由于元胞自动机是从具有时间离散性的自动机在空间上进行分割而演变过来的,故它十分便于使用计算机语言对其编程模拟。特别是对于方形结构的元胞自动机模型。3) 元胞自动机模型在建模时,只需要规定每个格点的演变规则和相邻几个细胞之间的作用方式,就可以让计算机算出结果。相比于其他模型,元胞自动机描述个体间的作用更直观、更具有针对性,而不需要考虑和简化各个反应元在整体中相遇和作用的概率。
基于以上优点,元胞自动机成为目前研究最多、应用最广的一种离散模型。元胞自动机的严格定义如下[47]:1) 周期性排列的元胞所组成的n维网络或其一部分;2)
网络中的每一个网格r在t = 0,1,2,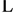 的状态都由如下一组布尔变量给定:
的状态都由如下一组布尔变量给定:
 ;
;
3) 每个网格r下一时刻的状态由演化规则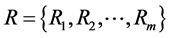 决定,表示为:
决定,表示为:
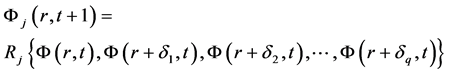
其中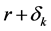 表示网格r的邻居。按照元胞自动机的数学定义,不难发现元胞自动机模型具有时空离散性。
表示网格r的邻居。按照元胞自动机的数学定义,不难发现元胞自动机模型具有时空离散性。
从网格维度来说,元胞自动机模型分为一维、二维、三维和高维元胞自动机。其中,最常见的是二维模型。对于二维元胞自动机来说,按照元胞的形状又可细分为三角、四方和六边形三种网络排列(图2)。
根据元胞自动机的定义,元胞自动机模型中的每一个格点随时间的变化情况,都是受其邻近的格点状态影响的(这些邻近的元胞我们称之为邻居)。邻居的选择很大程度上影响模型计算的速度和结果[48]。所以,如何选择邻居的分布范围,也是建立元胞自动机模型所要考虑的重要条件之一。原则上,邻居选择的范围和方式并没有具体的限制。但实际上,由于选择邻居范围扩大会导致演化规则复杂性增加,复杂性通常随近邻格点数增加,以指数形式增长,所以通常选择邻居的范围为与中心格点相接触的几个。最常见的邻居形状有两种:一种是Von Neumann邻居,它是由和中
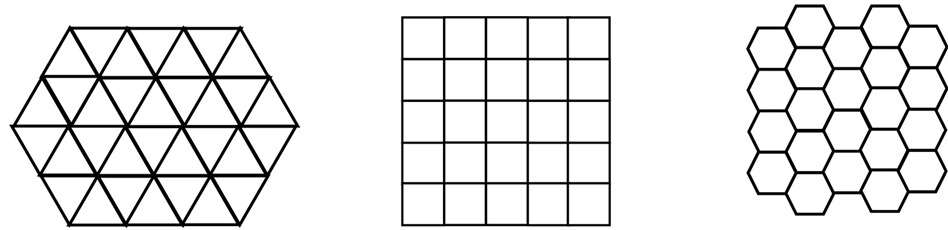
(a) 三角网络 (b) 四方网络 (c) 六边形网络
Figure 2. Three typical grid arrangements for 2D cellular automata model
图2. 常见二维元胞自动机划分方式
心元胞有边接触的4个元胞组成;另一种是Moore邻居,它在Von Neumann邻居的基础上,加上与中心元胞有点接触的一共8个元胞组成。图3展示了这两种邻居的分布情况。此外,还有钻石型和Margolus型邻居。
2.2. 元胞自动机在生物系统模拟中的特点
元胞自动机模型是基于计算机模拟的一种模型,相比于进行实体生物实验,计算机模拟实验具有以下3点优势[49]:1) 对于研究病理或者测试药物疗效的实验来说,尤其是人类疾病的实验,研究人员进行计算机模拟实验时并不需要从研究对象身上采样,也不需要在实体身上做实际操作。这样的模拟实验让理论研究者可以自由发挥其想象力和创造力,去设计各种各样的药物和治疗方法,而不需要担心错误的设想会加重病人病情甚至导致其死亡。2) 计算机模拟实验所花费的时间极短,进行一次实验的成本非常低。众所周知,进行生物体内或体外实验,是很复杂的一个过程。在试验过程中,实验员需要向样品添加许多昂贵的试剂,以及精心控制实验环境条件,如温度、ph值等。然而,模拟实验的对象是计算机,这在根本上决定了这项试验所需成本和时间几乎可忽略。3) 模拟实验的计算机程序编写完成后,只需要让计算机自动运行,就可以一次性进行成千上万组生物模拟实验,并对记录在存储介质中的实验结果进行统计分析。同时,这些实验的参数常量均保持不变。这样的设定使得理论生物学家只需要考虑变量的差异对结果造成的影响,而不需要对其他无关参量进行统计分析,研究的效率将大幅提升。
以上三点仅仅是计算生物学的计算模拟实验对
比实体生物实验的好处。而用元胞自动机设计的模型,不仅具有以上优点,还有更进一步的实际应用意义[50,51]。
a) 元胞自动机是一个微缩的复杂系统。单是一个只有两种状态和100个格点的元胞自动机模型就已经有2100(约1.27 × 1030)种可能状态。若是继续增加状态数和格点数,那么可能的状态会以指数形式增长。从统计物理学的角度来看,一个元胞自动机就是一个在有限时间内不可完全预测的复杂系统。这样的系统在模拟大量研究对象(如生物体内细胞)的时候,仿真度更高,模拟结果更加多样化,更具有现实意义。
b) 元胞自动机模型中状态之间的转换关系设计简单易懂。只需要画出马尔科夫链,所有人都能明白各个状态之间的转换关系。因此研究学者可以很轻松地设计生物模拟程序,也可以很方便地向其他从事非本方向的人说明自己所做的工作。
c) 只要计算机模拟程序正确,元胞自动机模型不会出现特殊的奇点。相比之下,微分模型和差分模型非常有可能因为噪声的扰动而导致模型出现发散或者超出理论极限值的情况。出现模拟数据异常的时候,使用微分方程模型的人,常常需要从模型设计和模拟程序设计这两方面找出出错原因。这对所有从事艾滋病发病理论模型研究的人来说都是想极力避免的事。
d) 元胞自动机模型中包含了时间和空间两方面的因素。与常微分模型相比,它具有空间尺度上的优势;与偏微分模型相比,元胞自动机得出最终结果的计算步骤少,方法简单;与网络模型相比,它又有展示各格点随时间变化的动态过程这优势。
然而,元胞自动机模型还是有一些不足之处。a) 系统的环境只能由邻近的格点和规则给定,不能够人为控制环境因素;b) 计算量(复杂度)随格点数增加而

Figure 3. Two neighborship definitions: (a) Von Neumann neighborhood, and (b) Moore neighborhood. The black grid is the central cell and the gray grids are the nighbor cells
图3. 两种邻居关系:(a) Von Neumann邻居;(b) Moore邻居。黑色格为中心元胞,灰色格为邻居元胞
增加, [47];c) 一个元胞与离它较远的元胞发生作用,要经过一段较长的传递时间,降低了系统的反应速率。
[47];c) 一个元胞与离它较远的元胞发生作用,要经过一段较长的传递时间,降低了系统的反应速率。
3. HIV免疫系统的元胞自动机模型
3.1. Santos元胞自动机HIV模型
2001年Zorzenon dos Santos发表了他们利用元胞自动机模型模拟出了T细胞和HIV在淋巴结中相互抗衡的情况[40]。作者在该模型中建立了一个 的二维的矩形网格阵列。每一个网格有4种可能的状态。这4种状态之间共有4条演变规则。设定特定的参数和初始条件,该模型能够模拟出HIV感染之后的三个特殊时期。HIV-元胞自动机模型是一个由
的二维的矩形网格阵列。每一个网格有4种可能的状态。这4种状态之间共有4条演变规则。设定特定的参数和初始条件,该模型能够模拟出HIV感染之后的三个特殊时期。HIV-元胞自动机模型是一个由 个等价格点组成的二维矩形网格阵列。每一个网格有4种可能的状态:健康,感染-A,感染-B和死亡。其中,健康细胞(H)代表免疫系统中未被感染的CD4+T细胞。感染-A、感染-B代表被HIV病毒感染后,带有HIV病毒RNA的CD4+T细胞,感染-A、感染-B具有产生和传播新的HIV病毒的能力。但是感染-A代表最近新感染的CD4+T细胞,感染-B代表将要死亡的受感染的CD4+T细胞,因此感染-A的感染能力比感染-B强。死亡细胞(D)代表被HIV感染后死亡的CD4+T细胞,它们能够被新产生的CD4+T细胞取代。
个等价格点组成的二维矩形网格阵列。每一个网格有4种可能的状态:健康,感染-A,感染-B和死亡。其中,健康细胞(H)代表免疫系统中未被感染的CD4+T细胞。感染-A、感染-B代表被HIV病毒感染后,带有HIV病毒RNA的CD4+T细胞,感染-A、感染-B具有产生和传播新的HIV病毒的能力。但是感染-A代表最近新感染的CD4+T细胞,感染-B代表将要死亡的受感染的CD4+T细胞,因此感染-A的感染能力比感染-B强。死亡细胞(D)代表被HIV感染后死亡的CD4+T细胞,它们能够被新产生的CD4+T细胞取代。
4种细胞之间的演变规则如下:
对于一个没有被感染的健康个体,所有的网格都处于健康状态,这个个体将一直保持健康状态。但是,如果他的免疫系统受到HIV的攻击,将有比例为PHIV的T细胞被感染成感染-A细胞(dos Santos等所设定的最初感染浓度PHIV = 0.05)。这些感染细胞会进一步感染系统中的健康细胞,进而使病人出现急性败血症。随后,由于模型边界条件的阻挡,感染-A细胞的数量将大幅减少,但系统中还残留有少量的感染-A细胞。此时病人进入了潜伏期。根据临床数据,在没有进行治疗的情况下,潜伏期可以维持2~8年。在这个时期里,HIV病毒携带者与正常人没有表面上的区别,因此这个时期也称为无症状期。随着时间推移,HIV携带者体内的感染-A细胞和感染-B细胞会感染健康T细胞,使得T细胞的数量逐渐减少,病毒数量逐渐增加。当健康T细胞数量少于正常浓度的20%时,这个病人被判定为艾滋病发病(图4)。这时候免疫系统无法正常识别入侵的抗原,这时候艾滋病病人会因免疫系统无法发挥正常作用而死亡。
然而,Matthew C. Strain 和 Herbert Levine 发现Santos的HIV-元胞自动机模型临床数据不符,该模型有两个重要的缺点[52]。首先在他们的模型中,用来表示病人最初被感染的细胞浓度PHIV大小为0.05,而临床测量得到的初始感染浓度的数量级为10−10。如果使用较小的PHIV,模型并不会出现三个典型的HIV感染过程。其次,临床观察数据显示,病人体内的病毒数在潜伏期的增长速度很慢,而到了AIDS发病时则突然暴增。这也与元胞自动机模型得到的HIV携带者体内病毒数逐渐增大到稳定值的结果不符。
3.2. 改进型Santos模型
尽管Santos的模型使用的参数与临床观测数据还
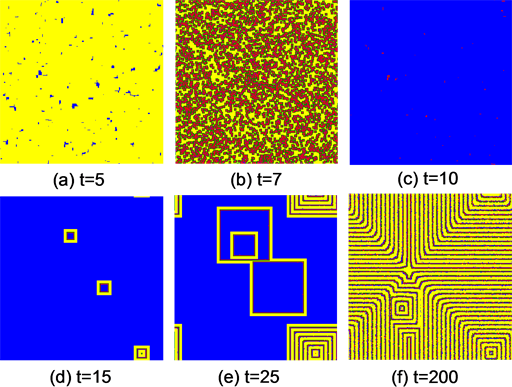
Figure 4. Snapshots of HIV infecting procedure of 2D CA model. Blue, yellow, green and red grids correspond to health, infected-A, infected-B, and dead cells, respectively
图4. HIV元胞自动机模型的感染动力学演化图。蓝色格点表示处于健康细胞,黄色格点表示感染A细胞,绿色格点表示感染B细胞,红色格点则是死亡细胞
(a)-(b) 表示病人处于急性期,体内大部分CD4+T细胞被HIV病毒感染;(c) 表示病人免疫系统压制病毒,但仍有少数病毒残留在体内;(d)-(e) 表示残留体内的HIV病毒破坏免疫系统,健康细胞数逐渐减少;(f) 表示免疫系统已被完全破坏,病人进入AIDS发病期
不能很好吻合,但这个模型还是得到了大家的认可。他们成功之处在于:使用一套简单的演化规则,通过系统演变得到了具有两种时间尺度和三种状态的结果。这个模型的模拟结果接近HIV的临床数据,揭示了模型中某些假设与真实的HIV感染机理是相吻合的。在后续几年时间里,不断有研究人员对基本的HIV-元胞自动机模型的鲁棒性和应用进行研究[53-60]。
Solovey等在[53]中测试了HIV-元胞自动机模型的几项重要参数。他们通过改变感染一个健康细胞所需要的近邻感染-A、感染-B型细胞数(RA, RB)来对应健康细胞抵抗力的变化,测试细胞抵抗能力对潜伏期的影响。结果表明,RB从1增加到9(RB = 9对应感染-B细胞没有感染能力,因为一个健康细胞最多有8个Moore邻居),模型仍然能够得到两种时间尺度上的变化过程。但是增加RB的值,会使得潜伏期变长。因此,增加健康细胞对感染-B的抵抗能力能够减少达成感染条件的概率,从而使潜伏期延长。
对于影响感染过程更大的一个参数RA来说,增大RA的值与增大RB的值得到的结果完全相反。通常来说,增大RA的值,意味着健康细胞对感染-A的抵抗力增强,将会使得潜伏期增大。然而,与上述猜想相反,RA从1增加到2的时候,潜伏期变得非常短。他们对此提出了一个解释:RA = 1时,每一个感染细胞都能形成一个传播波。这个波的波阵面在初始感染
阶段能够同时产生,并且同时消失。当RB = 2时,只有形成周围有两个感染-A细胞这种结构的时候,感染传播波才能产生。这就使得初始感染阶段的传播波不同步,进而使得两种时间尺度的效果消失。他们也尝试增加一个新参数的方法来控制感染健康细胞需要的感染-A细胞数。但结果表明,只有在RA = 1的时候,潜伏期的长度才达到最长。
接着,他们保持其他参数不变,从1到6改变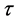 的值,来研究免疫系统对病毒的反应时间对发病过程的影响。模拟结果显示,发病过程与
的值,来研究免疫系统对病毒的反应时间对发病过程的影响。模拟结果显示,发病过程与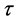 =4的时候相似。但在初始感染阶段,增加
=4的时候相似。但在初始感染阶段,增加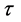 的值会使得感染-A细胞浓度峰值提高,并且初始感染时期的持续时间变长。
的值会使得感染-A细胞浓度峰值提高,并且初始感染时期的持续时间变长。
该研究表明,初始感染阶段感染细胞浓度达到峰值的平均时间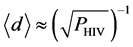 ,健康细胞和死细胞浓度最终的稳定点大约在
,健康细胞和死细胞浓度最终的稳定点大约在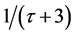 ,感染细胞浓度的稳定点在
,感染细胞浓度的稳定点在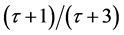 。
。
dos Santos的研究组随后进一步测试了元胞自动机基本模型的鲁棒性。在该研究中,他们使用了二维三角形网络格点和三维方形网络格点来模拟HIV的感染过程[54]。模拟结果表明,如果使用三角形网络格点,并且取RB = 3,得到的平均值与原HIV-元胞自动机模型的平均值相差不大。但如果选用三维网络格点,并令RB = 13,那么得到的平均结果与原模型相差甚远:
急性发病期会提前一个星期,潜伏期也显著缩短。这是因为相比于二维网络,三维网络中每一个细胞的邻居从8个增加到26个,这就使得HIV的传播速度和繁殖速度增快,进而使得潜伏期缩短。所以,如果认为淋巴结是一个分形结构,从模拟结果上看,它的维度更接近二维,而不是三维。
同时,他们的研究中也给出了一些函数关系。初始感染时期最大感染细胞浓度和与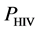 之间关系为:
之间关系为: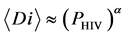 ,
,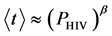 。对于二维网格,
。对于二维网格,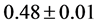
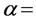 ,
,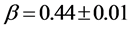 ;对于三维网格,
;对于三维网格,
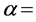 ,
,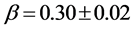 。而潜伏期长度与
。而潜伏期长度与 的关系则是
的关系则是 ,于二维网格,
,于二维网格,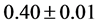
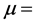 ;对于三维网格,
;对于三维网格,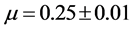 。如果RB的值从9增加到18,那么潜伏期的长度会从87周增加到120周。改变
。如果RB的值从9增加到18,那么潜伏期的长度会从87周增加到120周。改变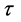 的值则对潜伏期长度无影响。
的值则对潜伏期长度无影响。
González等在原模型的基础上,增加了一种潜伏细胞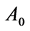 ,避免了
,避免了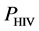 在取较小时初始感染期消失的问题[55]。新增的
在取较小时初始感染期消失的问题[55]。新增的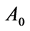 演化规则如下:
演化规则如下:
规则1: 细胞有
细胞有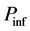 的概率被感染成
的概率被感染成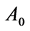 和
和 的概率被感染成
的概率被感染成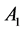 ;
;
规则4: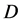 细胞有
细胞有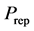 的概率被
的概率被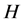 细胞取代,否则保持死亡状态;
细胞取代,否则保持死亡状态;
规则5: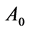 细胞保持
细胞保持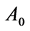 状态
状态 步,之后有
步,之后有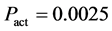 的概率被激活成
的概率被激活成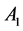 。
。
其他规则不变。
根据上述规则,他们得到了在低感染浓度时的HIV感染过程。然而,他们的模型仍有不足的地方:1) 初始感染浓度仍然偏大, 实测浓度
实测浓度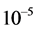 [38]。2) 潜伏细胞
[38]。2) 潜伏细胞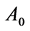 的设置过于牵强。平均来说,每一个
的设置过于牵强。平均来说,每一个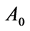 在
在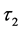 步之后向系统中增加
步之后向系统中增加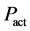 个
个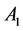 ,相当于在
,相当于在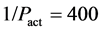 步后增加一个
步后增加一个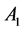 细胞。这样的规则实际上是人为地让系统在400周
≈ 8年后发病。
细胞。这样的规则实际上是人为地让系统在400周
≈ 8年后发病。
Strain等应用元胞自动机模型讨论了HIV病毒随机扩散对免疫动力学行为的影响[56],Meilke和Pandey提出了模糊相互作用的元胞自动机模型[57],Corne和Frisco在元胞自动机模型基础上提出了conformon-P模型,该模型对模型参数和初始浓度具有更好的鲁棒性[58]。Precharattana等考虑了更多状态的免疫细胞的元胞自动机模型[59],和更多种类免疫细胞的元胞自动机模型,包括CD4+T细胞,CD8+T细胞,树突细胞,并讨论了各种不同免疫细胞在HIV免疫中的作用[60]。
3.3. 三维HIV元胞自动机模型
通常元胞自动机模型都在二维网格上讨论,人们也研究了三维网格元胞自动机模型的性质[54,61,62]。在此,我们提出一个由一个L × L × L的立方体网格阵列组成的三维元胞自动机模型,其中每个格点及其邻居如图5所示,每个格点有26个邻居[62]。红色表示关注的格点(中心细胞)。黄色格点为第一类邻居,它们是最靠近红色格点的细胞,对中心细胞的影响效果最大。绿色格点为第二类邻居,它们到红色格点的距离比第一类邻居远,因此它们对中心细胞的影响效果比第一类邻居弱。蓝色格点为第三类邻居,它们到红色格点的距离最远,因此它们的作用效果最弱。
在3D元胞自动机模型中,共有4种细胞:H,感染-A,感染-B,和死亡细胞D,这4种细胞之间的作用关系服从如下规则:
模拟实验选用N = 100 × 100 × 100固定边界的网格, 模拟过程中每一步代表现实世界的一周,因此细胞状态更新频率为一周。在最开始,随机地向充满H细胞的网格中放入HIV,大约有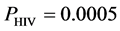 的H细胞被感染成感染-A细胞。随后,那些被感染成感染-A细胞的格点向外传播病毒,使更多H细胞受感染。新产生的感染细胞存活τ
+ 1步后变成死细胞。图6给出了一个二维截面上细胞的演化图。
的H细胞被感染成感染-A细胞。随后,那些被感染成感染-A细胞的格点向外传播病毒,使更多H细胞受感染。新产生的感染细胞存活τ
+ 1步后变成死细胞。图6给出了一个二维截面上细胞的演化图。
3D HIV-元胞自动机模型得到了典型的HIV感染的三个时期:急性发病期,潜伏期和AIDS发病期。由于不同个体间存在体质差异,得到的AIDS发病的区间介于2~20年。图7(a)~(c)展示了在4,9,16年发病的HIV携带者体内细胞浓度变化情况。第一个时期,

Figure 5. Neighborhood definition in 3D HIV model[62]. Red cube is the central cell, yellow cubes are the nearest neighbors, green cubes are the second nearest neighbors, and blue cubes are the third nearest neighbors of the center cube
图5. 3D HIV-元胞自动机模型邻居定义[62];红色表示中心细胞,黄色格点为第一类邻居,绿色格点为第二类邻居,蓝色格点为第三类邻居
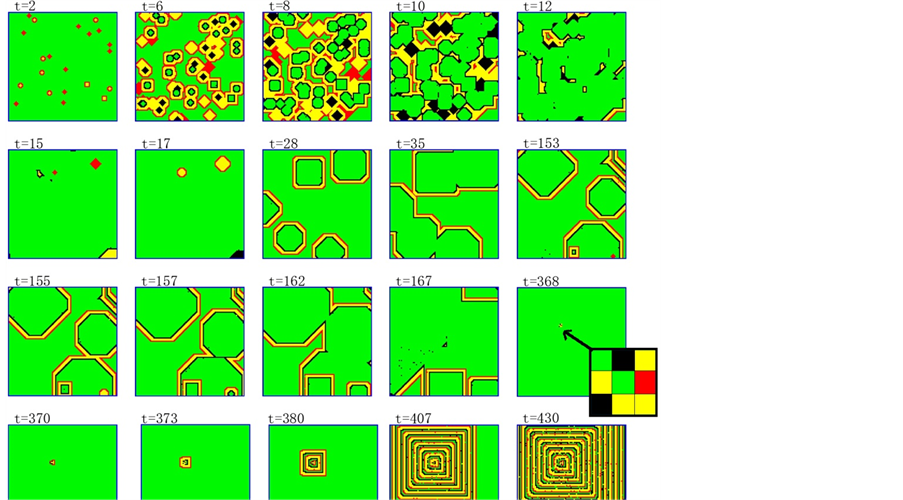
Figure 6. The 2D snapshots of HIV infecting evolution of 3D CA model[62]. Green, red, yellow and black grids correspond to health, infected-A, infected-B, and dead cells, respectively
图6. 二维截面上细胞的演化图[62]:其中绿色、红色、黄色和黑色分别表示健康、感染A、感染B和死亡细胞。其中在t = 368时的小图是产生了一个永久感染源,导致进入AIDS发病期

Figure 7. (a)-(c) Time evolution of healthy cells, infected cells and dead cells in three different individuals [62]; (d) The statistical result of HIV infection averaged over 2000 individuals. The error bars are for standard deviations
图7. (a)-(c) 不同个体在HIV感染后的健康细胞、感染细胞、死细胞随时间变化情况[62];(d) 2000个HIV携带者统计结果的平均值,误差棒为一倍标准差
也称为急性期,出现在HIV感染后的前几周。在这个时期里,H细胞数量急剧减少,然后又回升到正常水平。之后病人进入潜伏期(无症状期)。病人体内的H细胞和感染细胞会在这个时期相互对抗。免疫系统不能杀死所有的感染细胞,感染细胞也无法彻底破坏免疫系统。然而,当感染细胞在某个区域出现了一些特殊的细胞组合时,这些细胞组合非但不能被免疫系统杀死,反而能源源不断地产生大量感染细胞。我们称该细胞组合为永久感染源(图8),该永久感染源产生大量感染细胞并使其感染浓度大于阈值时,病人的免疫系统不能再抵挡HIV的进攻。在我们的模型中表现为感染细胞浓度大于某个值时,H细胞会急剧减少到正常水平的20%。这时候系统进入了AIDS发病期。
图7(d)是2000个模拟实验的统计结果。每个点代表健康细胞、感染细胞、死细胞浓度的平均值。在整体层面上看,健康细胞的浓度逐渐减少,感染细胞的浓度逐渐增大。在个体层面上看,健康细胞、感染细胞浓度在潜伏期会保持在一个相对稳定的值,到了AIDS期才会剧烈变化。图7(d)误差棒表示一倍标准差,在感染的前3年里,误差棒较小,这表示所有病人在前3年里的情况大致相同。在4~15年的区间里,误差棒较大。这表明不同病人的体质差异和HIV感染的随机性,导致了不同个体之间的发病情况有较大差异。相比于原HIV-元胞自动机模型,3D HIV-元胞自动机模型所使用的初始感染浓度PHIV达到10−4的水平,这是二维元胞自动机模型不能达到的低值。另外,在AIDS发病阶段,3D HIV-元胞自动机模型表现出的从潜伏期过渡到AIDS发病期的时间更短,更符合临床观察结果。
3.4. 淋巴结和血液中HIV元胞自动机模型
以上讨论的元胞自动机模型,模拟的主要是淋巴结中的HIV感染的动态过程。而实际上,AIDS感染的临床数据大多数是来自于血液数据。因此,Sompop Moonchai在原有的元胞自动机模型上,使用了两组平行的元胞自动机模型和一组关于病毒数量变化的关系式,来模拟淋巴结和外周血物质交换的过程[63]。他们增加的与淋巴结元胞自动机模型同时演化的外周血元胞自动机模型,较好地反映了外周血中病毒数的变化情况,使得模拟结果更接近临床测量值。
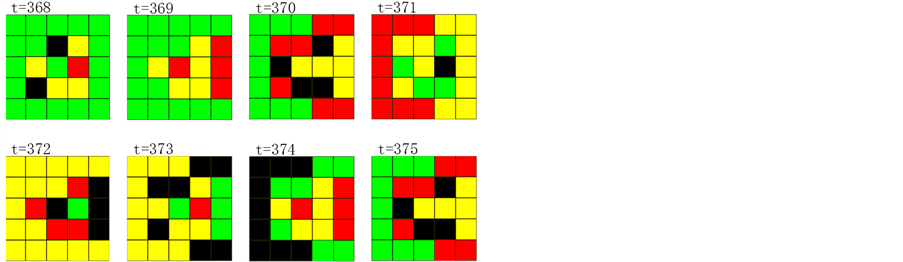
Figure 8. A perpetually infectious source can continuously produces infected cells, resulting in the AIDS onset[62]
图8. 永久感染源能持续不断地产生大量感染细胞,导致系统进入AIDS发病期[62]
双元胞自动机模型模拟外周血病毒数的建立过程与最初的元胞自动机模型类似,但有部分改动。模型初始化规则如下:系统最初处于健康状态,整个网络有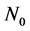 个格点,其中有
个格点,其中有 (
(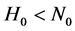 )个网格为健康细胞,其余为非激活状态。在受到HIV感染的时候,有
)个网格为健康细胞,其余为非激活状态。在受到HIV感染的时候,有 个格点被感染成
个格点被感染成 。而细胞的演变规则如下:
。而细胞的演变规则如下:
1) 非激活细胞演变规则:一个非激活的细胞有处于非激活状态的邻居,有 的概率被激活成
的概率被激活成 细胞,否则保持原状态。
细胞,否则保持原状态。
2) 健康细胞演变规则:a) 一个健康细胞被一个病毒感染的概率为: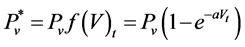 ,其中
,其中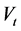 为t时刻系统内的病毒数;b)如果健康细胞有一个感染-A邻居,它被感染成感染-A的概率为
为t时刻系统内的病毒数;b)如果健康细胞有一个感染-A邻居,它被感染成感染-A的概率为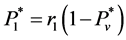 ;c) 如果健康细胞没有感染-A邻居,但它有R个感染-B邻居(2 <
R < 8),那它被感染成感染-A的概率为
;c) 如果健康细胞没有感染-A邻居,但它有R个感染-B邻居(2 <
R < 8),那它被感染成感染-A的概率为 ;d) 否则,它将保持原状态。
;d) 否则,它将保持原状态。
3) 感染-A,感染-B细胞演变规则与原模型相同。
4) 死亡细胞:a) 死亡细胞在下一步有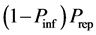 的概率变成健康细胞,有
的概率变成健康细胞,有 ,有
,有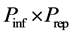 的概率保持死亡状态;b)
在经过a)步后,死亡细胞有
的概率保持死亡状态;b)
在经过a)步后,死亡细胞有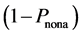 的概率被非激活细胞取代。
的概率被非激活细胞取代。
在淋巴结中病毒数变化方程如下:
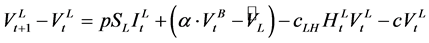

其中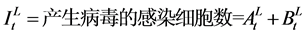 。在血液中病毒数变化方程如下:
。在血液中病毒数变化方程如下:
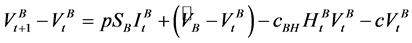

 .
.
在上述表达式中,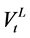 表示t时刻淋巴结中病毒数,
表示t时刻淋巴结中病毒数, 表示表示t时刻血液中病毒数,
表示表示t时刻血液中病毒数,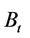
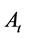 分别为感染-A,感染-B细胞数,
分别为感染-A,感染-B细胞数, 为健康细胞数,p为每个感染细胞平均产生病毒数,e表示病毒在淋巴结和血液系统中的循环,c是自由病毒死亡速率。迭代时间步长表示一周。利用上述规则,他们得到了健康细胞数随时间递减的模拟结果。
为健康细胞数,p为每个感染细胞平均产生病毒数,e表示病毒在淋巴结和血液系统中的循环,c是自由病毒死亡速率。迭代时间步长表示一周。利用上述规则,他们得到了健康细胞数随时间递减的模拟结果。
4. AIDS药物治疗的HIV元胞自动机模型
HIV的元胞自动机模型提出后,陆续有研究者使用元胞自动机模型来研究AIDS的治疗方法[55,64-67]。Sloot等在元胞自动机模型的基础上,增加了代表药物治疗的规则,使得元胞自动机模型能够模拟使用药物治疗病人体内的CD4+T细胞浓度变化情况[64]。在他们的模型中,他们通过改变规则1、3的方法,让元胞自动机模型具有模拟使用药物对HIV病毒逆转录和HIV蛋白合成的抑制的效果。新模拟规则如下:
规则1:在使用药物治疗期间,如果有一个感染-A近邻细胞,那它周围的N个健康细胞(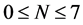 )将有
)将有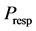 的概率在下一步变成感染-A。否则,8个近邻都变成感染-A。N的取值跟药物治疗效果有关。
的概率在下一步变成感染-A。否则,8个近邻都变成感染-A。N的取值跟药物治疗效果有关。
规则3:感染-B细胞的感染能力相比于感染-A较弱。
其他规则不变。
根据上述说明,作者在第300步对患者使用药物治疗(在第300步使用新规则)。模拟结果显示,在初始感染期后,健康细胞浓度缓慢减小,感染细胞浓度和死亡细胞浓度逐渐增大。在使用药物治疗后,CD4+T细胞数量有小幅回升,但持续治疗后,由于抗药性提高,治疗效果衰退,病人最终进入AIDS发病期。这样的结果与临床实验数据非常吻合。最后他们认为,相比于ODE/PDE模型,他们的模型能够通过修改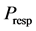 的值来更接近不同药物治疗方法的结果。
的值来更接近不同药物治疗方法的结果。
Precharattana利用元胞自动机模型讨论了Leukapheresis在艾滋病中的治疗作用,他们认为治疗效果对于药物的使用时间和频率具有很强的依赖关系[67]。
5. HIV元胞自动机的数学描述和软件编程
最近,Burkhead等人用图论的方法,给出元胞自动机模型数学语言上的演变规则,和稳定点向量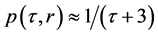 的公式[68]。元胞自动机模型的符号表示法如下:对于元胞自动机模型,
的公式[68]。元胞自动机模型的符号表示法如下:对于元胞自动机模型,
 。考虑到感染-A细胞要经过
。考虑到感染-A细胞要经过 步才变成感染-B细胞,所以输入带上每个格点的可能状态共有
步才变成感染-B细胞,所以输入带上每个格点的可能状态共有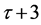 种,表示为
种,表示为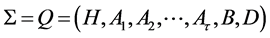 。在感染病毒后,系统有
。在感染病毒后,系统有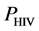 的格点处于
的格点处于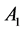 态,有
态,有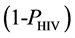 的格点处于
的格点处于 态。终止集合
态。终止集合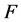 为空集,表示自动机不会再某个状态终止。每个格点和它的邻居可以用一个矩阵表示:
为空集,表示自动机不会再某个状态终止。每个格点和它的邻居可以用一个矩阵表示:
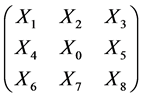
状态移动函数(演变规则)为:
1) 当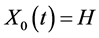 ,
,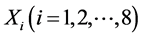 中若有一个
中若有一个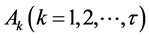 ,或者
,或者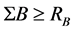 ,则有
,则有 ,否则
,否则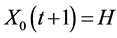 ;
;
2) 当 ,
,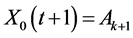 ;
;
3) 当 ,
,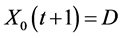 ;
;
4) 当 ,
,
由于系统的每个格点可以取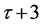 种状态,而每个格点(除了少数处于
种状态,而每个格点(除了少数处于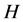 和
和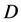 状态的点)在下一步都会变化成另一种状态。所以每个格点处于
状态的点)在下一步都会变化成另一种状态。所以每个格点处于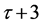 种状态是等概率的,处于每种状态的概率为
种状态是等概率的,处于每种状态的概率为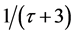 。因此系统处于最终稳定的状态时,四种状态数H,感染-A,感染-B,D占总网格数的比例为
。因此系统处于最终稳定的状态时,四种状态数H,感染-A,感染-B,D占总网格数的比例为
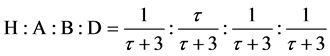
若将每一个元胞定义为空间中的一个空间微元,每一步定义为:时间上的一个时间微元,那么,我们可以把元胞自动机当成一个准连续的系统——它在时间和空间上都具有连续性。这也就是元胞自动机解偏微分方程的原理。Flora S. Bacelar等提出了一组带有时延项的微分方程来模拟HIV感染过程[69]。这个微分模型通过把元胞自动机模型中的演化规则转变为各细胞相互作用的概率,得到各细胞浓度变化速率。
这组含有9个参数和一个时延项的微分方程组如下:
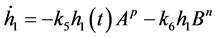
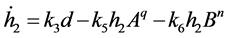
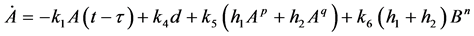
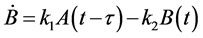
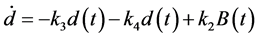
其中,ki、p、q为给定的参数,n为HIV-元胞自动机模型中感染H所需要的感染-B细胞数。
模型的结果结合Santos的HIV-元胞自动机模型的初始条件,通过计算机模拟实验,他们得到了健康细胞和感染细胞浓度随时间推移出现的三个特殊时期。结果显示,在感染的0~30周内,病人体内CD4+T细胞数量急剧减少然后又恢复到正常水平。在感染后的1~3年内,病人体内病毒数保持在较低浓度水平上。在感染后3~6年,病人体内病毒数增加,大部分病人出现AIDS发病症状。尽管他们能够模拟出HIV感染后的三个特殊时期,但该模型仍有两个不尽如人意的地方:1) 模型中使用的参数过多;2) 在AIDS发病后,CD4+T细胞浓度震荡时间过长,这都使得的这模型未能完整反映HIV感染的真正动力学原理。
关于HIV的元胞自动机模拟,由于计算速度和内存的限制,典型的元胞数目一般是几万到几百万。Hecquet等讨论了如何在更大的元胞网络上进行优化和并行编程模拟[70]。Baldazzi等开发了一个关于HIV元胞自动机的软件平台(C-ImmSim),该软件不仅能用于HIV的动力学讨论,也能讨论药物治疗HIV (HAART)的动力学过程[71]。
6. 总结和展望
本文对HIV元胞自动机模型进行了综述,讨论了如何利用元胞自动机模型研究HIV–免疫系统的动力学行为,特别是三阶段发展过程,也讨论了使用元胞自动机模型来研究AIDS的治疗方法。这些研究从理论上加深我们对HIV病毒与免疫系统复杂动力学的了解,并为临床医学各种可能的治疗方案提供了理论基础和参考。
这些模型虽然已经考虑了与HIV感染相关的基本重要因素,但相对于实际复杂的HIV和免疫系统之间的相互作用而言,仍然做了很大的简化。而这些简化必然忽略了HIV–免疫系统的很多复杂和重要的动力学行为,如何发展更符合生物实际的HIV元胞自动机模型,从而更有效讨论可能的AIDS的治疗方法,显然是HIV元胞自动机未来研究的一个很重要的发展方向。
HIV具有两个重要的特征使得其感染进程不同于普通的病毒。首先,HIV的一个致命特征就是它所感染和杀伤的首要目标正好是免疫系统中最重要成分之一,CD4+T细胞。其次,由于HIV的逆转录酶缺乏校正机制,因此病毒RNA在逆转录过程中具有极高的突变率。 突变有可能造成病毒多肽的改变,使得记忆性的抗体和杀伤性T细胞无法识别。于是,免疫系统针对未变异前的HIV所激活的特异性B细胞和杀伤T细胞就变得毫无用处,而必须活化能识别变异病毒多肽的新的免疫细胞。然而,由于获得性免疫的有效激活需要一到两个星期的时间,在这期间突变病毒可能已经感染了大量的目标细胞,并早已经大量复制了。而在HIV每次复制时还可能发生新的突变,这就可能使得病毒的演化总能领先于抗击它的免疫细胞一步。在现有的HIV元胞自动机模型基础上,进一步考虑病毒的变异特性,将揭示更多的HIV动力学性质。
我们的研究表明[62],当HIV感染病人进入潜伏期后,如果感染细胞在某个区域出现了一些特殊组合的细胞团,形成永久感染源后,感染细胞不能被免疫系统有效杀死,反而能源源不断地产生大量感染细胞,导致病人的免疫系统不能再抵挡HIV的进攻,但感染细胞浓度大于某个值时,H细胞会急剧减少到正常水平的20%,这时候系统进入了AIDS发病期。所以,HIV元胞自动机模型表明,永久感染源的形成是导致病人从潜伏期进入AIDS发病期的决定因素。而在真实病人系统里,AIDS发病过程中是否存在这样一种永久感染源,则直接关系到HIV元胞自动机模型研究的合理性,也为HIV研究提出了一个有趣的实验问题。
近年来,也有不少研究人员使用元胞自动机模型来研究其他病毒的发病和传播等过程[72-75]。Beauchemin等提出将元胞自动机用于流感病毒的研究中[72],Santos等利用三层元胞自动机研究了登革热流行病毒的感染传播行为[73],Xiao和Gharib-Zahedi等使用元胞自动机模型模拟B型肝炎病毒在人体的感染过程[73,74]。这些研究表明,元胞自动机模型能够很好地模拟一些病毒的重要特征。因此,元胞自动机模型是一种非常好的生物模拟模型,如何能够推广用于其他病毒的动力学模拟,也将是元胞自动机在病毒研究领域中,未来发展的一个重点方向。
致谢
本课题获得如下基金项目支持:国家杰出青年科学基金(11125419),国家自然科学基金面上项目(31370830),和福建省高校领军人才资助计划。
参考文献 (References)
- [1] Becker, M.H. and Joseph, J.G. (1988) AIDS and behavioral change to reduce risk: A review. American Journal of Public Health, 78, 394-410.
- [2] Barre-Sinoussi, F., Chermann, J.C., Rey, F., et al. (1983) Isolation of a T-lymphotropic retrovirus from a patient at risk for acquired immune deficiency syndrome (AIDS). Science, 220, 868- 871.
- [3] Gallo, R.C., Salahuddin, S.Z., Popovic, M., et al. (1984) Frequent detection and isolation of cytopathic retroviruses (HTLVIII) from patients with AIDS and at risk for AIDS. Science, 224, 500-503.
- [4] Levy, J.A., Hoffman, A.D., Kramer, S.M., et al. (1984) Isolation of lymphocytopathic retroviruses from San Francisco patients with AIDS. Science, 225, 840-842.
- [5] Chun, T.W., Engel, D., Mizell, S.B., et al. (1999) Effect of interleukin-2 on the pool of latently infected, resting CD4+T cells in HIV-1-infected patients receiving highly active anti-retroviral therapy. Nature Medicine, 5, 651-655.
- [6] Uenishi, R., Hase, S., Keng, T.K., et al. (2007) HIV/AIDS in Asia: The shape of epidemics and their molecular epidemiology. Virologica Sinica, 6, 004.
- [7] Mayer, K.H. and Beyrer, C. (2007) HIV epidemiology update and transmission factors: Risks and risk contexts—16th International AIDS Conference epidemiology plenary. Clinical Infectious Diseases, 44, 981-987.
- [8] 钟进彦, 张栗, 柳建发 (2010) 艾滋病的流行研究进展. 地方病通报, 6, 72-74.
- [9] Wei, X., Ghosh, S.X., Taylor, M.E., et al. (1995) Viral dynamics in human immunodeficiency virus type 1 infection. Nature, 373, 117-122.
- [10] Finzi, D., Hermankova, M., Pierson, T., et al. (1997) Identification of a reservoir for HIV-1 in patients on highly active antiretroviral therapy. Science, 278, 1295-1300.
- [11] Bassetti, S., Battegay, M., Furrer, H., et al. (1999) Why is highly active anti-retroviral therapy (HAART) not prescribed or discontinued. JAIDS Journal of Acquired Immune Deficiency Syndromes, 21, 114-119.
- [12] Sharkey, M.E., Teo, I., Greenough, T., et al. (2000) Persistence of episomal HIV-1 infection intermediates in patients on highly active anti-retroviral therapy. Nature Medicine, 6, 76-81.
- [13] Bassetti, S., Battegay, M., Furrer, H., et al. (1999) Why is highly active anti-retroviral therapy (HAART) not prescribed or discontinued? Journal of Acquired Immune Deficiency Syndromes, 21, 114-119.
- [14] Dinoso, J.B., Kim, S.Y., Wiegand, A.M., et al. (2009) Treatment intensification does not reduce residual HIV-1 viremia in patients on highly active antiretroviral therapy. PNAS, 106, 9403- 9408.
- [15] Sharkey, M.E., Teo, I., Greenough, T., et al. (2000) Persistence of episomal HIV-1 infection intermediates in patients on highly active anti-retroviral therapy. Nature Medicine, 6, 76-81.
- [16] Dean, M., Carrington, M., Winkler, C., Huttley, G.A., Smith, M.W., Allikmets, R., et al. (1996) Genetic restriction of HIV-1 infection and progression to AIDS by a deletion allele of the CKR5 structural gene. Science, 273, 1856-1862.
- [17] Rosenberg, E.S., Altfeld, M., Poon, S.H., Phillips, M.N., Wilkes, B.M., Eldridge, R.L., Robbins, G.K., D’Aquila, R.T., Goulder, P.J. and Walker, B.D. (2000) Immune control of HIV-1 after early treatment of acute infection. Nature, 407, 523-526.
- [18] Novina, C.D., Murray, M.F., Dykxhoorn, D.M., Beresford, P.J., Riess, J., Lee, S.K., Collman, R.G., Lieberman, J., Shankar, P. and Sharp, P.A. (2002) siRNA-directed inhibition of HIV-1 infection. Nature Medicine, 8, 681-686.
- [19] Pantaleo, G., Graziosi, C. and Fauci, A.S. (1993) The immunopathogenesis of human immunodeficiency virus infection. New England Journal of Medicine, 328, 327-335.
- [20] Kaplan, E.H. (1990) An overview of AIDS modeling. New Directions for Program Evaluation, 46, 23-36.
- [21] Phillips, A.N. (1996) Reduction of HIV concentration during acute infection: Independence from a specific immune response. Science, 271, 497-499.
- [22] Perelson, A.S. and Weisbuch, G. (1997) Immunology for physicists. Reviews of Modern Physics, 69, 1219.
- [23] Perelson, A.S. and Nelson, P.W. (1999) Mathematical analysis of HIV-1 dynamics. SIAM Review, 41, 3-44.
- [24] Cohn, M. and Mata, J. (2007) Quantitative modeling of immune responses. Immunological Reviews, 216, 5-8.
- [25] Chavali, A.K., Gianchandani, E.P., Tung, K.S., Lawrence, M.B., Peirce, S.M. and Papin, J.A. (2008) Characterizing emergent properties of immunological systems with multi-cellular rulebased computational modeling. Trends in Immunology, 29, 589- 599.
- [26] Li, X.H., Wang, Z.X., Lu, T.Y. and Che, X.J. (2009) Modelling immune system: Principles, models, analysis and perspectives. Journal of Bionic Engineering, 6, 77-85.
- [27] Nowak, M.A., May, R.M. and Anderson, R.M. (1990) The evolutionary dynamics of HIV-1 quasispecies and the development of immunodeficiency disease. AIDS, 4, 1095-1103.
- [28] Coffin, J.M. (1995) HIV population dynamics in vivo: Implications for genetic variation, pathogenesis, and therapy. Science, 267, 483-489.
- [29] Nowak, M. and May, R.M. (2000) Virus dynamics: Mathematical principles of immunology and virology. Oxford University Press, Oxford.
- [30] Perelson, A.S. (2002) Modelling viral and immune system dynamics. Nature Reviews Immunology, 2, 28-36.
- [31] Wang, G. and Deem, M.W. (2006) Physical theory of the competition that allows HIV to escape from the immune system. Physical Review Letters, 97, Article ID: 188106.
- [32] Wodarz, D. (2007) Kill cell dynamics: Mathematical and computational approaches to immunology. Springer, Berlin.
- [33] Hernandez-Vargas, E.A. and Middleton, R.H. (2013) Modeling the three stages in HIV infection. Journal of Theoretical Biology, 320, 33-40.
- [34] Hershberg, U., Louzoun, Y., Atlan, H. and Solomon, S. (2001) HIV time hierarchy: Winning the war while, loosing all the battles. Physica A, 289, 178-190.
- [35] Lin, H. and Shuai, J.W. (2010) A stochastic spatial model of HIV dynamics with an asymmetric battle between the virus and the immune system. New Journal of Physics, 12, 043051.
- [36] Weisbuch, G. and Atlan, H. (1988) Control of the immune response. Journal of Physics A: Mathematical and General, 21, L189-L192.
- [37] Dayan, I., Stauffer, D. and Havlin, S. (1988) Cellular automata generalization of the Weisbuch-Atlan model for immune response. Journal of Physics A: Mathematical and General, 21, 2473-2476.
- [38] Pandey, R.B. and Stauffer, D. (1990) Metastability with probabilistic cellular automata in an HIV infection. Journal of Statistical Physics, 61, 235-240.
- [39] Pandey, R.B. (1991) Cellular automata approach to interacting cellular network models for the dynamics of cell population in an early HIV infection. Physica A, 179, 442-470.
- [40] Zorzenon dos Santos, R.M. and Coutinho, S. (2001) Dynamics of HIV infection: A cellular automata approach. Physical Review Letters, 87, 168102.
- [41] Codd, E.F. (1968) Cellular automata. Academic Press, Inc., Waltham.
- [42] Gardner, M. (1970) Mathematical games: The fantastic combinations of John Conway’s new solitaire game “life”. Scientific American, 223, 120-123.
- [43] Wolfram, S. (1983) Statistical mechanics of cellular automata. Reviews of Modern Physics, 55, 601.
- [44] Wolfram, S. (1984) Cellular automata as models of complexity. Nature, 311, 419-424.
- [45] Wolfram, S. (1994) Cellular automata and complexity: Collected papers. Addison-Wesley, Reading.
- [46] Maerivoet, S. and De Moor, B. (2005) Cellular automata models of road traffic. Physics Reports, 419, 1-64.
- [47] Chopard, B. and Droz, M. (1998) Cellular automata modeling of physical systems. Cambridge University Press, Cambridge.
- [48] Mei, S.S., Billings, S.A. and Guo, L.Z. (2005) A neighborhood selection method for cellular automata models. International Journal of Bifurcation and Chaos, 15, 383-393.
- [49] Toffoli, T. and Margolus, N. (1987) Cellular automata machines: A new environment for modeling. MIT Press, Cambridge.
- [50] Coveney, P.V. and Fowler, P.W. (2005) Modelling biological complexity: A physical scientist’s perspective. Journal of the Royal Society Interface, 2, 267-280.
- [51] Celada, F. and Seiden, P.E. (1992) A computer model of cellular interactions in the immune system. Immunology Today, 13, 56- 62.
- [52] Strain, M.C. and Levine, H. (2002) Comment on “dynamics of HIV infection: A cellular automata approach. Physical Review Letters, 89, Article ID: 219805.
- [53] Solovey, G., Peruani, F., Ponce Dawson, S. and Zorzenon dos Santos, R.M. (2004) On cell resistance and immune response time lag in a model for the HIV infection. Physica A: Statistical Mechanics and Its Applications, 343, 543-556.
- [54] Figueirêdo, P.H., Coutinho, S. and Zorzenon dos Santos, R.M. (2008) Robustness of a cellular automata model for the HIV infection. Physica A: Statistical Mechanics and Its Applications, 387, 6545-6552.
- [55] González, R.E.R., de Figueirêdo, P.H. and Coutinho, S. (2013) Cellular automata approach for the dynamics of HIV infection under antiretrovial therapies: The role of the virus diffusion. Physica A, 392, 4717-4725.
- [56] Strain, M.C., Richman, D.D., Wong, J.K. and Levine, H. (2002) Spatiotemporal dynamics of HIV propagation. Journal of Theoretical Biology, 218, 85-96.
- [57] Mielke, A. and Pandey, R.B. (1998) A computer simulation study of cell population in a fuzzy interaction model for mutating HIV. Physica A, 251, 430-438.
- [58] Corne, D.W. and Frisco, P. (2008) Dynamics of HIV infection studies with cellular automata and conformon-P systems. BioSystems, 91, 531-544.
- [59] Precharattana, M., Triampo, W., Modchang, C., Triampo, D. and Lenbury, Y. (2010) Investigation of spatial formation involving CD4+ T cells in HIV/AIDS dynamics by a stochastic cellular automata model. International Journal of Mathematics and Computers in Simulation, 4, 135-143.
- [60] Precharattana, M. and Triampo, W. (2014) Modeling dynamics of HIV infected cells using stochastic cellular automaton. Physica A, 407, 303-311.
- [61] Mannion, R., Ruskin, H.J. and Pandey, R.B. (2002) Effects of viral mutation on cellular dynamics in a Monte Carlo simulation of HIV immune response model in three dimensions. Theory in Biosciences, 121, 237-245.
- [62] Mo, Y.B., Ren, B., Yang, W.C. and Shuai, J.W. (2014) The 3-dimensional cellular automata for HIV infection. Physica A, 399, 31-39.
- [63] Moonchai, S., Lenbury, Y. and Triampo, W. (2010) Cellular automata simulation modeling of HIV infection in lymph node and peripheral blood compartments. International Journal of Mathematics and Computers in Simulation, 4, 124-134.
- [64] Sloot, P., Chen, F. and Boucher, C. (2002) Cellular automata model of drug therapy for HIV infection. In: Cellular Automata, Springer, Berlin, 282-293.
- [65] Benyoussef, A., El HafidAllah, N., ElKenz, A., Ez-Zahraouy, H. and Loulidi, M. (2003) Dynamics of HIV infection on 2D cellular automata. Physica A, 322, 506-520.
- [66] Shi, V., Tridane, A. and Kuang, Y. (2008) A viral load-based cellular automata approach to modeling HIV dynamics and drug treatment. Journal of Theoretical Biology, 252, 24-35.
- [67] Precharattana, M., Nokkeaw, A., Triampo, W., Triampo, D. and Lenbury, Y. (2011) Stochastic cellular automata model and Monte Carlo simulations of CD4+ T cell dynamics with a proposed alternative leukapheresis treatment for HIV/AIDS. Computers in Biology and Medicine, 41, 546-558.
- [68] Burkhead, E.G., Hawkins, J.M. and Molinek, D.K. (2009) A dynamical study of a cellular automata model of the spread of HIV in a lymph node. Bulletin of Mathematical Biology, 71, 25- 74.
- [69] Bacelar, F.S., Andrade, R.F.S. and Santos, R.M. (2010) The dynamics of the HIV infection: A time-delay differential equation approach.
- [70] Hecquet, D., Ruskin, H.J. and Crane, M. (2007) Optimisation and parallelization strategies for Monte Carlo simulation of HIV infection. Computers in Biology and Medicine, 37, 691-699.
- [71] Baldazzi, V., Castiglione, F. and Bernaschi, M. (2006) An enhanced agent based model of the immune system response. Cellular Immunology, 244, 77-79.
- [72] Beauchemin, C., Samuel, J. and Tuszynski, J. (2005) A simple cellular automaton model for influenza A viral infections. Journal of Theoretical Biology, 232, 223-234.
- [73] Santos, L.B., Costa, M.C., Pinho, S.T.R. and Andrade, R.F.S. (2009) Periodic forcing in a three level cellular automata model for a vector-transmitted disease. Physical Review E, 80, 016102.
- [74] Xiao, X., Shao, S.H. and Chou, K.C. (2006) A probability cellular automaton model for hepatitis B viral infections. Biochemical and Biophysical Research Communications, 342, 605-610.
- [75] Gharib-Zahedi, M.R. and Ghaemi, M. (2012) Kinetics of hepatitis B virus infection: A cellular automaton model study. Journal of Paramedical Sciences, 3, 2008-4978.

NOTES
*通讯作者。
