Advances in Applied Mathematics
Vol.07 No.01(2018), Article ID:23551,11
pages
10.12677/AAM.2018.71010
The G Expansion Method of Satisfying a Variable Coefficient Equation and New Exact Solutions of Rlw-Burgers Equation
Xin Wang
College of Information Science and Technology, Hainan University, Haikou Hainan
Received: Dec. 21st, 2017; accepted: Jan. 18th, 2018; published: Jan. 25th, 2018

ABSTRACT
Based on the basic idea of the
expansion method, we construct a kind of New G method, and make the function G satisfy a class of variable coefficient Bernoulli equation. The RLW-Burgers equation is solved by this method, and several new explicit traveling wave solutions of the equation are obtained. It has been proved that this kind of satisfying variable coefficient equation G expansion method for solving nonlinear partial differential equations solutions is feasible and effective.
Keywords:RLW-Burgers Equation, Variable Coefficient Bernoulli Equation, G Expansion Method, Exact Solutions
满足变系数方程的G展开法及RLW-Burgers 方程的新精确解
王鑫
海南大学信息科学技术学院,海南 海口
收稿日期:2017年12月21日;录用日期:2018年1月18日;发布日期:2018年1月25日

摘 要
本文借鉴
展开法的基本思路,构造了一类新的G展开法,并令其中的函数G满足一类变系数Bernoulli方程。用此法对RLW-Burgers方程进行了求解,得到了该方程的多个新的显式行波解。事实证明,这类满足变系数方程的G展开法对于求解非线性偏微分方程的精确解是有效可行的。
关键词 :RLW-Burgers方程,变系数Bernoulli方程,G展开法,精确解

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
求解非线性偏微分方程的精确解是目前科技发展中解决非线性问题的关键。现在已有多种可以求得非线性偏微分方程精确解的常用方法,其中
展开法 [1] ,是一种较为简单可行的计算方法。本文就是以
展开法为基础,构造了一类
展开法,其中
为互不相等的自由参数,并令其中的函数
满足一类变系数Bernoulli方程。通过此展开法,求得了RLW-Burgers方程的多个新的精确解。
RLW-Burgers方程
(1)
其中
。该方程可以用来描述河渠中水波表面的传播性态,它的行波解的存在性及解的性质已由文献 [2] 和文献 [3] 给出;振荡激波解也由文献 [4] 得到;通过未知函数的变换及待定系数法,文献 [5] 得到了该方程的显式行波解;该方程的古典对称和势对称也在文献 [6] 中得到了研究,并通过推广的双曲函数法和Lie变换群得到了该方程的精确解;文献 [7] 通过改进的G展开法得到了方程的含参数的多种形式的精确解。
2. 满足变系数方程的G展开法
将非线性偏微分方程
(2)
作行波变换,令
,
,则化为常微分方程
,
设方程(2)的解为
(3)
其中
为待定的常数,
为互不相等的自由参数,参数
可以通过齐次平衡法确定;其中函数
满足一类变系数Bernoulli方程
(4)
这里
均为
的任意函数。通过借助符号计算软件Mathematica,我们可以得到方程(4)的解:
(5)
这里
为积分常数。
将(3)式代入(2)式,并结合(4)式,合并
的同幂次项,并令
的各次幂的系数为零,从中求出
,再将求得的
代入(5)式,得到
函数,最后将
与
代入(3)式即得到方程(2)的解。
3. RLW-Burgers方程新的精确解
设方程(1)有行波解
,其中
表示波速,从而方程(1)化为
,
将上式两边关于
进行积分并化简,得
, (6)
其中M为积分常数。设方程(1)的解能够表示成多项式
,且
满足一类变系数Bernoulli方程
,
其中
为
的任意函数。利用齐次平衡法,我们有
,得
。则方程(1)的解表示为
, (7)
由方程(4)和(7)式可得
将上面
的各阶导数全部代入(6)式,并合并
的同幂次项,比较方程两端的系数,化简得
:
。
用Mathematica软件对以上代数方程组进行求解,我们得到了以下五组解:
1)
,
,
,
,
,
,
其中
均为任意常数。将上面求得的
代入(5)式,有
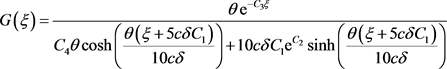 ,
,
其中
均为任意常数。再由(7)式,我们得到了RLW-Burgers方程的解为
这里的
。
2)
,
,
,
,
,
,
,
,
其中
均为任意常数。将上面求得的
代入(5)式,有
,
再由(7)式,我们得到了RLW-Burgers方程的解为
,
这里的
。
3)
,
,
,
,
,
,
其中
均为任意常数。将上面求得的
代入(5)式,有
,
再由(7)式,我们得到了RLW-Burgers方程的解为
这里的
。
4)
,
,
,
,
,
,
,
其中
均为任意常数。将上面求得的
代入(5)式,有
,
再由(7)式,我们得到了RLW-Burgers方程的解为
,
这里的
。
5)
,
,
,
,
,
,
,
其中
均为任意常数。将上面求得的
代入(5)式,有
,
再由(7)式,我们得到了RLW-Burgers方程的解为
,
这里的
。
4. 总结
本文构造了一类满足变系数Bernoulli方程的,且含有自由参数
的
展开法。用此方法对RLW-Burgers方程进行了求解,得到了该方程的多个新的显式行波解。事实证明,该方法不仅可以求解非线性偏微分方程,而且可以得到方程更为丰富的精确解。
基金项目
国家自然科学基金(11601109),海南省自然科学基金(117066)。
文章引用
王 鑫. 满足变系数方程的G展开法及RLW-Burgers方程的新精确解
The G Expansion Method of Satisfying a Variable Coefficient Equation and New Exact Solutions of Rlw-Burgers Equation[J]. 应用数学进展, 2018, 07(01): 80-90. http://dx.doi.org/10.12677/AAM.2018.71010
参考文献 (References)
- 1. Wang, M.L., Li, X.Z. and Zhang, J.L. (2008) The (G’/G)-Expansion Method and Travelling Wave Solutions of Non-linear Evolution Equations in Mathematical Physics. Physics Letters A, 372, 417-423.
https://doi.org/10.1016/j.physleta.2007.07.051
- 2. 王明新. 非线性抛物形方程[M]. 北京: 科学出版社, 1993.
- 3. 黄正洪, 夏莉. RLW-Burgers方程行波解的性质[J]. 重庆师范学院学报(自然科学版), 1998, 15(1): 24-28.
- 4. 谈骏渝. RLW-Burgers方程的一类解析解[J]. 数学的实践与认识, 2001, 31(5): 545-549.
- 5. 刘金枝, 吴爱祥. RLW-Burgers方程的显式行波解[J]. 南华大学学报(自然科学版), 2004, 18(3): 18-20.
- 6. 鲍春玲, 苏道毕力格, 韩雁清. RLW-Burgers方程的势对称及其精确解[J]. 应用数学进展, 2016, 5(1): 112-120.
- 7. 王鑫. RLW-Burgers方程的新显式行波解[J]. 应用数学进展, 2017, 6(4): 619-626.





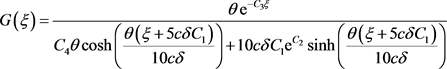 ,
,