Advances in Applied Mathematics
Vol.07 No.04(2018), Article ID:24622,5
pages
10.12677/AAM.2018.74046
2-Arc-Regular Graphs of Square-Free Order and Prime Valency
Menglin Ding
School of Statistic and Mathematic, Yunnan University of Finance and Economic, Kunming Yunnan
Received: Apr. 8th, 2018; accepted: Apr. 20th, 2018; published: Apr. 27th, 2018

ABSTRACT
A graph G is called -arc regular, if is regular on s-arc set. Feng’s paper [1] determined all one-regular graphs of square-free order and prime valent are Cayley graphs. Quite a lot of works with small valency are known, see [2] [3] [4] . We determined all 2-arc-regular graphs of square-free order and prime valency, where the degree .
Keywords:Automorphism Group, Arc-Regular Graph, Cayley Graph

平方自由阶素数度2-弧正则图
丁梦琳
云南财经大学统计与数学学院,云南 昆明

收稿日期:2018年4月8日;录用日期:2018年4月20日;发布日期:2018年4月27日

摘 要
称一个图为s-弧正则图,如果图的全自同构群在图的s弧集上是正则的。Feng等在 [1] 中证明了素数度的1-弧正则图都是Cayley图,随后出现一些小度数图的研究,见 [2] [3] [4] 。本文即确定了平方自由阶素数度的2-弧正则图,其中度数t满足 。
关键词 :自同构群,弧正则图,凯莱图

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
一个图与其全自同构群密切相关,全自同构群是图论中的一个基本且重要的研究对象,一个图的全自同构群越大,图的对称性越好,故寻找一个图的自同构群便成为研究图的首要却也十分困难的任务。正则图是一类简单图,图的许多性质都是从正则图的研究开始的,比如正则图的连通性,对称性,所以研究正则图的性质成为图论的一个活动领域。本文便完全确定了平方自由阶的素数度2-弧正则图,其中度 。
本文所得主要结果如下:
定理1.1. 设G为2n阶t度的2-弧正则图,其中n为平方自由的且至少包含三个素因子,t素数,且 ,则 ,且G满足:
, ,其中 ,
2. 预备引理
为了证明以上定理,我们给出几个重要的结果。
首先是含有二面体Sylow 2-子群的有限群,参见[ [5] ,引理2.4]。
引理2.1. 设G为一个含二面体Sylow 2-子群的有限群,M是G的最大奇数阶正规子群,则G/M同构于下列群之一:
1) (二面体) 2-子群;
2) 或 ;
3) 的包含 的子群,其中 为奇素数幂。
下面给出关于局部本原图的一个性质。参见[ [6] ,定理4]。
引理2.2. 设 为平方自由阶k度, 的G-局部本原联通图。假设G在VG上传递且G不是完全二部图,则下述之一成立:
1) ,2nk为平方自由的,k为nk的最小素因子,G为二面体
上的Cayley图;
,2nk为平方自由的,k为nk的最小素因子,G为二面体
上的Cayley图;
2)
,其中M为平方自由阶的,X为几乎单群且
a) ;
b) 或者 ,其中 ;
c) 或 ;
d) , ,且 ,或者 或者 , ;
e) G为Lie型单群 , ,或者 ,G为d维典型群, 。或者 ,
。且 有至多两个轨道并且G为T-边传递图,特别地,如 ,则 满足[ [6] ,表3]。
下面给出平方自由阶弧传递3度图的一个引理,参见 [7] 。
引理2.3. 设G为2n阶弧传递3度图,其中n为平方自由的且至少包含三个素因子,则下述之一成立:
1) 可解,且 ;
2) ,其中 为一素数。
下面的定理稍微改进了Praeger,参见[ [8] ,定理4.1]的一个著名结果,见 [9] 。
命题2.1. 设G为素数度 -弧正则图,且假设 在VG上至少有3个轨道,则下述之一成立:
1) N在VG半正则, 为 -弧正则图,且G为 的一个正规N-覆盖;
2) ,其中 , ;
3) 如果X有一正规子群 ,则 为 -弧正则,且是 的一个正规N/M-覆盖。
群 的极大子群是知道的,下面我们给出一个引理,参见 [10] 。
引理2.4. 设 , ,p为素数,则G的极大子群同构于下列群之一:
1) ,其中 ,且 ;
2) ,其中 ,且 ;
3) 
4) ,其中 ,或 ;
5) ,其中 ;
6) ,其中 ;
7) , 为奇素数;
8) ,n为偶数。
接下来我们给出 极大子群 [10] 的一个推论。
推论2.1. 设 为 的子群,其中 ,t都是奇素数。则 。
证明:因为q为奇素数, ,H包含在 的极大子群里,我们逐一验证引理2.4的可能的情况。(1)~(3)由阶数算是不可能的,排除。(7)和(8)中,因为q为奇素数,没有p值使之存在,排除。(4)和(5)中,H为 满足。(6)中, 中没有20阶的子群,排除。综上,H只可能为 ,我们得到 。
通过Magma [8] ,我们可以检验一个图是否为3度2-弧正则图。我们给出一个2-弧正则图关于 的例子。
例子2.1. 设 为作用在20个点上的置换群。设:
a = (1, 3)(2, 13)(4, 5)(6, 10)(7, 12)(8, 19)(9, 14)(11, 15)(16, 17)(18, 20);
b = (1, 16, 4)(3, 5, 17)(6, 20, 7)(8, 15, 9)(10, 12, 18)(11, 19, 14);
c = (1, 18)(2, 8)(3, 20)(4, 16)(5, 17)(6, 11)(7, 9)(10, 15)(12, 14)(13, 19);
证明:设 ,则 , 且 ,因此 是 -弧正则3度图。而且这个图是在同构意义下的自同构群为 的2-弧正则3度图。
接下来给出一个2-弧正则图关于 的例子。
例子2.2. 设 为作用在30个点上的置换群。设
e = (3, 16)(4, 20)(5, 26)(6, 9)(7, 28)(8, 14)(10, 18)(11, 12)(13, 29)(15, 23)(17, 30)(19, 25)(21, 22)(24, 27);
f = (1, 14, 8)(2, 7, 28)(3, 27, 10)(4, 9, 13)(5, 12, 21)(6, 20, 29)(11, 26, 22)(15, 30, 19)(16, 18, 24)(17, 23, 25);
g1 = (1, 2)(3, 25)(4, 7)(5, 29)(6, 15)(8, 17)(9, 23)(10, 27)(13, 26)(14, 30)(16, 19)(18, 24)(20, 28)(21, 22);
g2 = (1, 2)(4, 21)(5, 11)(6, 25)(7, 23)(8, 14)(9, 19)(10, 30)(12, 26)(13, 24)(15, 28)(17, 18)(20, 22)(27, 29)。
证明:设 用Magma计算可知: ,
,因此 和 是 -弧正则3度图。更多的,这两个图是同构意义下,以 作为全自同构群的唯一的两个不同构的2-弧正则3度图。
3. 定理证明
设G为2n阶素数度t度的2-弧正则图,其中 , , , 为不同的素数。设 , 表示图G的全自同构群。
定理3.1. 假设A可解,则图G不存在。
证明:如果图G存在,首先假设G是完全二部图,则 ,当 时, 是不可解的,与A可解矛盾。当 时, 且G是3度图,此时 , ,则 ,而3度2-弧正则图的点稳定子群阶为6,矛盾。
假设G不是完全二部图,因为素数度的图一定是局部本原图,所以G满足引理2.2,又因为A是可解的,所以G满足引理2.2 (1),于是 , ,则 与图G为2-弧正则图矛盾。综上,图G不存在,定理得证。
下面我们给出定理1.1的证明。
定理3.2. 设 ,A不可解,则图G满足定理3.1。
证明:因为G为t度的2-弧正则图,所以 , ,设A的Sylow 2-子群 ,则 或 。
如果 为循环群,因为Sylow 2-子群是循环群的有限群都是可解的,所以推出矛盾。于是 ,A满足引理2.1。设M为A的最大的奇数阶正规子群,逐一分析A/M的可能性,如果A/M为可解的,则由M为可解群,可推出A可解,矛盾。于是 或满足引理2.1 (3)。如果 ,则 ,这与 矛盾。所以 ,其中 ,p为素数。
断言: 且 。
假设 ,因为 ,所以 ,所以 且f不是2的方幂。因为G为2-弧正则图,由引理3.1中类似的分析,可知G不是完全二部图。由假设,A不可解,所以G满足引理2.2 (2)部分。
于是可以设 ,N是平方自由阶的,X为几乎单群, 。
考虑到 ,可推出 且 。下面逐一验证引理2.2 (2) (i)-(v)。
因为
,所以(i)和(ii)直接可排除;假设满足(iii),则
且
或
,均与假设矛盾。假设满足(iv),则
,
且
,
。因为
,所以
,如果
,则
且
,矛盾。如果
,则
或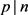 ,且
,总之,
,所以
,这与
矛盾。
与假设矛盾。假设满足(iv),如果A为d维典型群,此时
,矛盾。如果
,则与
矛盾。
,且
,总之,
,所以
,这与
矛盾。
与假设矛盾。假设满足(iv),如果A为d维典型群,此时
,矛盾。如果
,则与
矛盾。
于是断言成立。
假设M在VG上传递,则 为偶数,这与 是奇数矛盾。
假设M在VG上有两个轨道,记为 , ,设 ,由 [9] ,之所以 ,是因为 , ,下证 ,因为 , 为block,故如果不成立,则满足 。
( ,矛盾。)而且,因为A在VG上传递,所以 。由Frattini论断, ,则 为可解的,且M可解,故 可解。又因为 , ,故A可解。矛盾。
假设M在VG上至少有三个轨道,由命题2.1,由M诱导的正规商图 为 -弧正则图,其
中
为平方自由的, 。设
,
,
,则
。设
,
,
,则
。设 ,Y为 的极大子群,由断言,我们知道q为奇素数,所以由推论得 。最后,因为A不可解且 ,由引理2.3,我们得到 ,且 为奇素数。因为 ,其中n是平方自由的奇素数,所以 , ,
且 ,得 且 定理得证。
问题:虽然本文已得到一些较好的结果,但还是有许多的不足之处,例如:没有得到对于 时的平方自由阶s-弧正则图的一般结论。这将是一个巨大的工作。
文章引用
丁梦琳. 平方自由阶素数度2-弧正则图
2-Arc-Regular Graphs of Square-Free Order and Prime Valency[J]. 应用数学进展, 2018, 07(04): 369-373. https://doi.org/10.12677/AAM.2018.74046
参考文献
- 1. Feng, Y.Q. and Li, Y.T. (2011) One-Regular Graphs of Square-Free Order of Prime Valency. European Journal of Combinatorics, 32, 261-275. https://doi.org/10.1016/j.ejc.2010.10.002
- 2. Fang, X., Wang, J. and Xu, M.Y. (2002) On 1-Arc-Regular Graphs. European Journal of Combinatorics, 23, 785-791. https://doi.org/10.1006/eujc.2002.0579
- 3. Feng, Y.Q. and Kwak, J.H. (2004) One-Regular Cubic Graphs of Order a Small Number Times a Prime or Prime Square. Journal of the Australian Mathematical Society, 76, 345-356. https://doi.org/10.1017/S1446788700009903
- 4. Feng, Y.Q. and Kwak, J.H. (2007) Cubic Symmetric Graphs of Order a Small Number Times a Prime or a Prime Square. Journal of Combinatorial Theory, Series B, 97, 627-646. https://doi.org/10.1016/j.jctb.2006.11.001
- 5. Pan, J.M., Ding, S.Y. and Liu, Y. (2014) Finite Arc-Regular Graphs of Prime Valency. Scientia Sinica Mathematica, 44, 307-315. https://doi.org/10.1360/012014-1
- 6. Li, C.H., Lu, Z.P. and Wang, C.X. (2015) On Edge-Transitive Graphs of Square-Free Order. European Journal of Combinatorics, 22, 41-46. https://doi.org/10.1016/j.ejc.2014.10.005
- 7. Ling, B. and Lou, B.G. (2017) Arc-Transitive Cubic Graphs of Order Four Times an Odd Square-Free Integer. Journal of Algebra and Its Applications, 16, 213-225. https://doi.org/10.1142/S0219498817502139
- 8. Bosma, W., Cannon, J. and Playoust, C. (1997) The MAGMA Algebra System I: The User Language. Journal of Symbolic Computation, 24, 235-265. https://doi.org/10.1006/jsco.1996.0125
- 9. Biggs, N. (1992) Algebraic Graph Theory. 2nd Edition, Cambridge University Press, New York.
- 10. Dickson, L.E. (1958) Linear Groups with an Expositions of the Galois Field Theory. Dover.