Journal of Electrical Engineering
Vol.05 No.02(2017), Article ID:21081,5
pages
10.12677/JEE.2017.52025
Measurement Uncertainty Evaluation of Integrated Calibration System for High Voltage Metering Device
Chengliang Niu, Erjie Huang, Jie Liang, Qiufeng Shang
Electronics and Communication Engineering, North China Electric Power University, Baoding Hebei

Received: Jun. 1st, 2017; accepted: Jun. 19th, 2017; published: Jun. 22nd, 2017

ABSTRACT
Existing integrated high voltage metering device overcame the drawbacks of traditional metering device. It replaced the existing metering device. Its calibration and testing also aroused concern of the majority of researchers. But for the traditional high-voltage energy metering device, its error is calculated by the synthetic error method. The error calculated in this way is not in conformity with the basic principle stipulated by the International Electrotechnical commission. In this paper, on the basis of integrated calibration system design, it makes use of uncertainty theory to analyze uncertainty sources in high voltage metering device integrated calibration system. It gave complete uncertainty evaluation program and calculation process. It got expanded uncertainty of the power measurement error and got the final complete energy metering error. By calibration sys- tem uncertainty assessment, the reliability of measurement results can be evaluation within reason. It provided a quantitative basis for energy metering device performance evaluation.
Keywords:Energy Measurement, Integration of Calibration, Error, Measurement Uncertainty
高压计量装置一体化校验系统不确定度评定
牛成亮,黄尔杰,梁杰,尚秋峰
华北电力大学电子与通信工程系,河北 保定
收稿日期:2017年6月1日;录用日期:2017年6月19日;发布日期:2017年6月22日

摘 要
目前出现的高压一体化计量装置克服传统计量装置的种种弊端,正逐渐代替现有的计量装置,其校验和测试工作也引起广大研究人员的关注。但是对于传统型高压电能计量装置,它的误差采用综合误差法计算得到,这样计算得到的误差并不符合国际电工委员会规定的基本原则。本文在一体化误差校验系统的设计基础上,利用计量学中的不确定度理论,对高压计量装置一体化误差校验系统的不确定度来源分析,提出系统的不确定度评定方案,并给出具体分析计算过程,获得电能计量误差的扩展不确定度,得到电能计量误差的完整表达。不确定度评定对于校验系统提高评价测量结果的可信度有重要的意义,同时也为电能计量装置综合性能评估提供了量化的依据。
关键词 :电能计量,一体化校验,误差,测量不确定度

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
传统型高压电能计量装置的误差是通过综合误差方法计算电力电压互感器误差、电流互感器误差和低压电能表三部分的误差再综合得到,国际电工委员会(IEC)规定的基本原则:所有的仪表装置和计量装置的误差都必须经过实际的精确测量,没有经过实际测量,仅仅通过其他测量计算出来的引用电压、电流和功率因数组合的误差,不能作为评价装置基本误差的依据 [1] [2] 。传统误差校验方法并不符合这一规定,所以,高压计量一体化校验成为研究热点。高压计量装置一体化是指电子式互感器和计量终端以及分压网络共同封装到断路器箱体,不再独立设计和测试。传统校验方法不能对一体化装置进行全面准确的测量,所以为了保证校验的准确性有必要对计量装置进行整体校验以及不确定度评定。
本文在一体化误差校验系统的设计基础上,利用计量学中的不确定度理论,对高压计量装置一体化误差校验系统的不确定度来源分析,提出系统的不确定度评定方案,并给出具体分析计算过程,测量不确定度作为评定测量结果好坏的一个重要指标。测量不确定度数值越小,表示测量结果的可信度越高,测量水平越高,使用价值也越大。其结果可有效地衡量所测的综合误差量的可信程度,并且电能计量装置一体化校验的不确定度也为电能计量装置综合性能评估提供了量化的依据。
2. 高压计量装置一体化误差校验系统
2.1. 系统构成
高压计量一体化校验系统分为三个模块,分别是高压标准信号源、脉冲检测装置和后台校验平台。系统原理框图如图1所示。
一体化校验工作过程分为4步:
1) 后台软件平台向高压标准源发送电力参数,控制三相低压标准源的输出。2) 三相低压标准信号源输出低压信号,该信号通过升压器和升流器转变为标准的高压大电流信号,使标准计量通道和被检计量通道拥有相同的输入条件。3) 脉冲检测装置同时采集标准计量通道和被检计量通道产生的脉冲,并在脉冲采集完成后将脉冲相关数据发送给后台校验平台。4) 后台校验软件对数据进行分析、处理,并显示校验结果。
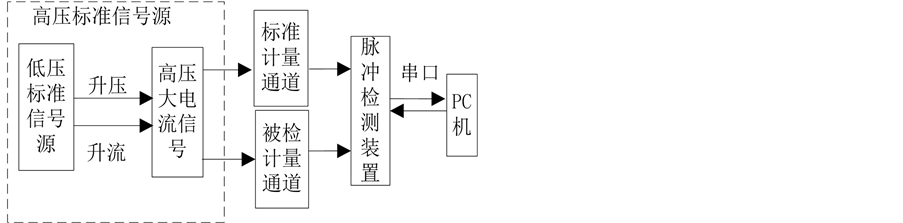
Figure 1. Verification platform diagram
图1. 校验平台组成框图
2.2. 测量条件和测量数据
一体化误差校验采用的标准表经计量站检定,其准确级为0.1级;标准电压互感器和电流互感器的精度等级经测量均为0.01级,能够作为标准通道。误差计算、数据分析和显示由在Microsoft Visual Studio2010平台上开发的C#窗体软件界面来完成。
在室温环境下、相对湿度小于80%的条件下,在设备经过预热稳定后开始测试,表1所示为在cosφ = 0.5 L、额定电压、电流分别为额定值的100%、50%、20%、10%、5%条件下测得的10组误差数据。
3. 一体化校验系统不确定度分析及计算
3.1. 校验系统不确定度来源分析
A、由测量误差的重复性引入的标准不确定度分量U(r01) (A类评定)
B、由测量误差时引入的不确定度分量U(r02) (B类评定)
U(r02)由标准表测量引入的标准不确定度u1、标准电压互感器测量引入的标准不确定度u2和标准电流互感器测量时引入的标准不确定度u3构成 [3] [4] 。各部分标准器件引入的不确定度是相互独立的,不会产生影响。
3.2. 单位校验系统不确定度评定
单位校验系统不确定度评定不确定度分量计算
不确定度是计量学的概念,它反映了基准标准、检定测试、校准比对的水平,同时,作为量值溯源依据,它还反映了测试设备的质量,分为A类不确定度、B类不确定度、标准不确定度及扩展不确定度 [5] 。
1) A类标准不确定度:不确定度各分量可用实验标准方差S表征,常采用贝塞尔公式计算有限次的实验标准差S:
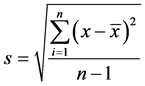 (1)
(1)
对表2所示的10组误差数据求取平均值,并计算实验标准差:
计算合成样本标准差SP:
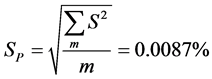
标准不确定度U(r01):
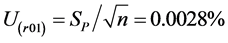
2) B类不确定度:先求出不确定度来源各分量的分布系数kj及灵敏系数cj。再计算B类不确定度。
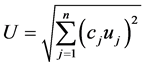
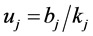 (2)
(2)
标准电能表误差及电压互感器、电流互感器误差引起的不确定度分量均服从均匀分布,分布系数kj等于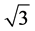 。cj为B类各不确定度分量的灵敏系数,一般值取1。B类不确定度误差项如表3所示。
。cj为B类各不确定度分量的灵敏系数,一般值取1。B类不确定度误差项如表3所示。
其中:rr为标准表误差;fTV为标准电压互感器误差;fTA为标准电流互感器误差。计算标准不确定度U(r02):
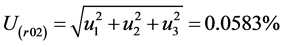
3) 合成标准不确定度UC:
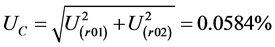 (3)
(3)
Table 1. Relative error
表1. 相对误差
Table 2. Mean and experimental standard deviation of the data
表2. 数据的均值和实验标准差
Table 3. Uncertainty errors of class B
表3. B类不确定度误差项
4) 扩展不确定度U:由校验系统除被检计量装置以外其他测量环节引入的测量误差由扩展不确定度表示。它代表了所测量的值和真实值之间的分散性,能够反映校验系统的测量水平。扩展不确定度的数值越小,说明真值所处的范围越小,测量结果越具有可信度,反之亦然。
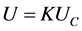 (4)
(4)
系数K是置信因数又称包含因子。在电能表标准装置中,K值一般取2,置信率P = 95%。则扩展不确定度: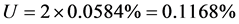 。
。
根据以上测量数据估算出被校电能计量装置在功率因数为0.5 L时,扩展不确定度: 。
。
5) 电能相对误差:
由表2所示10组测量数据的均值可求出最佳误差估值:
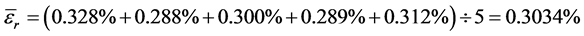
用合成误差表示计量装置电能累计的相对误差为:
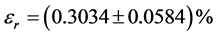
用扩展不确定度表示电能相对误差:
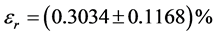
4. 结论
采用所构建的高压电能计量装置一体化校验系统,克服了传统校验装置的缺点,实现了电能计量装置一体化封装后的综合误差测试,并从计量学的角度对电能计量装置的综合误差测量结果进行了不确定度评定,使校验的结果具有可靠性。根据不确定度报告给出的测量结果,通过合成误差以及扩展不确定度得出电能计量误差的完整表达,合理地评价校验系统的结果可信度,对电能计量的校验具有重要意义,同时,有助于进一步提高我们电能计量的整体水平。
文章引用
牛成亮,黄尔杰,梁 杰,尚秋峰. 高压计量装置一体化校验系统不确定度评定
Measurement Uncertainty Evaluation of Integrated Calibration System for High Voltage Metering Device[J]. 电气工程, 2017, 05(02): 204-208. http://dx.doi.org/10.12677/JEE.2017.52025
参考文献 (References)
- 1. 岳长喜, 候兴哲, 章述汉, 等. 10kV高压电能计量装置整体校验台的校准[J]. 电测与仪表, 2010, 47(S2): 132-136.
- 2. 蒋卫, 杨华云, 江波. 高压三相组合互感器三相检定方法及其实现研究[J]. 电测与仪表, 2011, 48(7): 46-49.
- 3. 张福州, 刘刚, 江波, 等. 高压三相组合互感器三相检定法的接线方式对检定准确性的影响[C]//中国电机工程学会. 中国电机工程学会青年学术会论文集: 2014年卷. 2.
- 4. 张能, 廖慧敏, 吴永云,等. 三相组合互感器检定装置研究[J]. 自动化与仪器仪表, 2012(4): 41-43.
- 5. 郭琳云, 尹项根, 张乐平, 等. 基于高压电能表的计量装置在线校验技术[J]. 电力自动化设备, 2009, 29(12): 79- 82.
