Pure Mathematics
Vol.07 No.04(2017), Article ID:21348,9
pages
10.12677/PM.2017.74038
Sieve of Multiple Content and Subtle Effects of  的妙用
的妙用
Sishun Lu
Linyi University, Linyi Shandong

Received: Jun. 23rd, 2017; accepted: Jul. 7th, 2017; published: Jul. 13th, 2017

ABSTRACT
We introduce the notions of multiple content and parallel arithmetic series. Based on the overlap law of multiple contents and properties of parallel arithmetic progressions, we discuss the appearance rule of multiples in the series of natural numbers. As applications, we prove the even number Goldbach’s conjecture and the twin prime conjecture.
Keywords:Multiple Content, Overlap Law, Covering Theorem, Parallel Arithmetic Series, Sieve of Both Sides
倍数含量筛法与恒等式( )的妙用
)的妙用
鲁思顺
临沂大学,山东 临沂

收稿日期:2017年6月23日;录用日期:2017年7月7日;发布日期:2017年7月13日

摘 要
本文挖掘出倍数含量及等差项同数列的概念,根据倍数含量重叠规律及等差项同数列的性质,对自然数列中倍数出现规律作了深入的探讨。作为应用,我们证明了偶数哥德巴赫猜想与孪生素数猜想。
关键词 :倍数含量,重叠规律,覆盖定理,等差项同数列,两筛法

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
1.1. 偶数2n表为两自然数和的式子共有n种形式
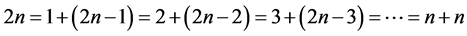
记作 为有序对偶集合:
为有序对偶集合:
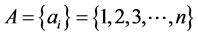
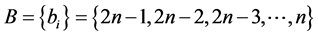
如果把A(B)中的加数是合数及1的式子都筛除干净,若还有剩余的式子,说明偶数2n能表示为两素数之和。
1.2. 小于n的相差为2的数对共有n-2种形式

记作:
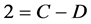
其中C(D)为有序对偶集合

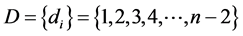
如果把C(D)中的数是合数的都筛除干净,若能证明剩余的式子有无穷多,则说明存在无穷多相差为2的素数对。
2. 简单比例单筛
2.1. 倍数含量
在连续的n个自然数的集合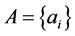 中,自然数
中,自然数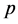 的倍数个数有
的倍数个数有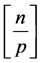 或
或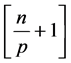 (
(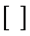 为去尾取整)。
为去尾取整)。
定义1: 中数的个数
中数的个数 与自然数
与自然数
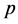 的比值
的比值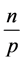 ,叫做自然数
,叫做自然数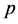 的倍数含量.在
的倍数含量.在 中非
中非 的倍数含量为
的倍数含量为 。
。
易知, 的倍数含量与
的倍数含量与 成正比例关系,
成正比例关系,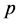 的倍数个数与
的倍数个数与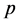 的倍数含量的正负误差的绝对值小于1。
的倍数含量的正负误差的绝对值小于1。
2.2. 倍数含量重叠规律
引理1 [1] :在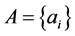 里
里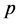 的倍数含量中,
的倍数含量中, 的部分倍数含量,也就是
的部分倍数含量,也就是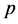 的倍数的含量中的
的倍数的含量中的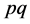 的倍数含量,占有
的倍数含量,占有
 。
。
证明:在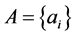 里,合数
里,合数 的倍数含量为
的倍数含量为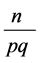 ,而
,而 。证毕
。证毕
注:明筛与暗筛
由引理1知,明筛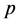 的倍数含量,同时也按照
的倍数含量,同时也按照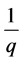 比例暗筛去了
比例暗筛去了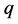 的部分倍数含量。
的部分倍数含量。
推论1 [1] :筛除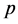 的倍数含量后,在剩下的非
的倍数含量后,在剩下的非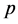 的倍数含量中,
的倍数含量中,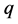 的倍数含量有
的倍数含量有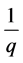 。
。
证明: 。证毕
。证毕
由推论1知,筛除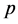 的倍数含量之后,欲筛除剩余部分中
的倍数含量之后,欲筛除剩余部分中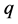 的倍数含量,只需对剩余部分
的倍数含量,只需对剩余部分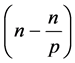 ,再筛除
,再筛除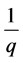 ,即可。
,即可。
推论2 [2] :在 中的n个数中,依次筛除
中的n个数中,依次筛除 的倍数含量后,在非
的倍数含量后,在非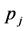 的倍数含量中,
的倍数含量中,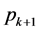 的倍数含量占有
的倍数含量占有 ,非
,非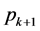 的倍数含量占有(
的倍数含量占有(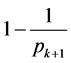 )
)
证明:用数学归纳法证明
(I) 当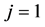 时
时
在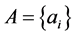 中,根据倍数含量的定义,
中,根据倍数含量的定义,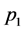 ,
,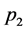 ,
, 的倍数含量分别为
的倍数含量分别为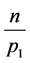 ,
,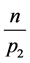 ,
,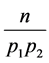 。
。
根据引理1及推论1,易得
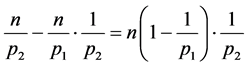 。
。
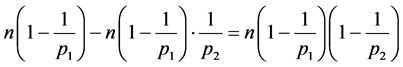 。
。
则命题成立。
(II) 假设当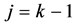 时命题成立
时命题成立
即在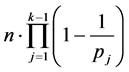 中
中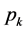 的倍数含量为
的倍数含量为
 (1)
(1)
非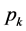 的倍数含量为:
的倍数含量为:
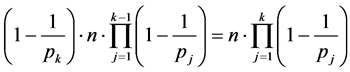 (2)
(2)
下边证明当 时,命题成立。
时,命题成立。
由p的任意性及假设可知:
 在
在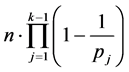 中的倍数含量分别是:
中的倍数含量分别是:
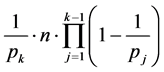
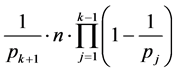 (3)
(3)
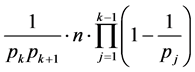 (4)
(4)
(3)~(4)
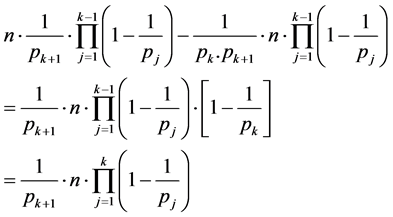 (5)
(5)
(2)~(5)
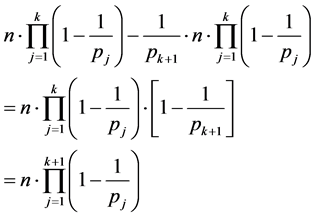
综合(I) (II),命题成立。
我们把推论2中,按照 在
在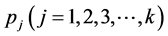 的倍数含量占有比例规律,依次递筛
的倍数含量占有比例规律,依次递筛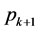 的倍数含量,求出非
的倍数含量,求出非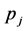 倍数含量的方法,叫做倍数含量简单比例单筛法。
倍数含量的方法,叫做倍数含量简单比例单筛法。
例1:带有1至210编号210名同学站在操场上,带操
老师第一次下口令,让编号是2的倍数的同学坐下,
老师第二次下口令,让编号是3的倍数的同学坐下,
老师第三次下口令,让编号是5的倍数的同学坐下,
老师第四次下口令,让编号是7的倍数的同学坐下,
问最后,还有几位同学站着?
解:因为210是2,3,5,7的公倍数,2,3,5,7的倍数含量与倍数个数相等,用推论2计算,得

3. 加强比例单筛法
3.1. 覆盖定理 [2]
引理2(覆盖定理):设 为小于
为小于 的素数,即使间隔最小,即
的素数,即使间隔最小,即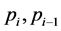 为孪生素数时,仍有
为孪生素数时,仍有

证明:因为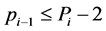 (
(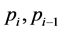 为孪生素数时,等号取得)
为孪生素数时,等号取得)
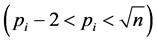

所以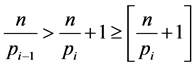 。证毕
。证毕
3.2. 加强方法
在筛除2,3的倍数时,我们不妨用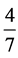 和
和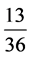 代替原来的2,3的倍数(含量)占有比例
代替原来的2,3的倍数(含量)占有比例 ,在筛除
,在筛除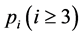 的倍数时,依据引理2(覆盖定理)按照比例
的倍数时,依据引理2(覆盖定理)按照比例 筛除,这种筛除方法我们称之为倍数含量加强比例单筛法。
筛除,这种筛除方法我们称之为倍数含量加强比例单筛法。
 ,
,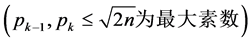
4. 等差项同数列及其性质 [2]
大偶数2n表为两数和的式子共有n种形式:
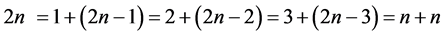
前项集合: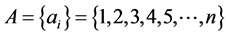 ,
,
后项集合: ,
,
要是把前项集合A,后项集合B中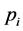 (
(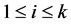 ,
, 的最大素数)倍数的式子都筛除干净,若还有剩余的式子,就说明大偶数能表为两素数和的式子。
的最大素数)倍数的式子都筛除干净,若还有剩余的式子,就说明大偶数能表为两素数和的式子。
问题是,筛去A中的一个素数的倍数(如3的倍数,是一个数列),要带走B中的一个数列,这两个数列,都是等差数列,项数相同。下面我们看它们之间有什么性质。
4.1. 等差项同数列
定义2:如果两个正整数等差数列,项数相同,公差相等,则称这两个数列为等差项同数列。
定义3:设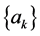 长度为
长度为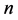 的,公差为
的,公差为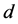 的等差数列,若
的等差数列,若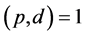 ,则称
,则称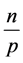 为
为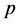 在数列
在数列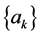 中的倍数含量,
中的倍数含量,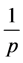 为其占有比例。
为其占有比例。
引理3:在长度为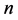 的,公差为
的,公差为 的等差数列
的等差数列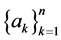 中,若自然数
中,若自然数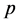 满足
满足 ,则
,则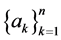 中
中 的倍数个数有
的倍数个数有 或
或 个。
个。
证明:只需证明当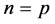 时
时 中有且只有一个
中有且只有一个 的倍数。
的倍数。
设数列为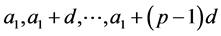 ,则它们中任意两个元素对
,则它们中任意两个元素对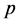 的余数不相同,若不然设
的余数不相同,若不然设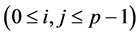
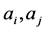 关于
关于 同余,从而可得
同余,从而可得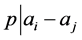 ,即
,即 ,这是不可能的。所以
,这是不可能的。所以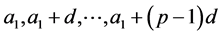 关于
关于 互不同余,从而其中有且只有一个
互不同余,从而其中有且只有一个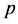 的倍数。证毕
的倍数。证毕
4.2. 等差项同数列的性质
引理4 (等差项同数列的性质):若两数列为等差项同数列,则自然数
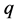 在两数列中的倍数含量相等。即
在两数列中的倍数含量相等。即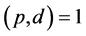
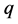 的倍数含量在两个数列中所占比例相等。
的倍数含量在两个数列中所占比例相等。
证明:由引理3显然。
引理4说明,明处是筛去A中的一个素数p的倍数(如3的倍数,是一个数列),带走B中的一个数列,即带走了B中的q 的部分(与筛去A中同样多少的)倍数含量。再进行下步筛去q
的部分(与筛去A中同样多少的)倍数含量。再进行下步筛去q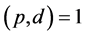 的倍数含量时,只对剩余部分筛,就可以了。
的倍数含量时,只对剩余部分筛,就可以了。
主筛与从筛
在通过筛合数而筛式子的过程中,称筛除 中素数
中素数 的倍数含量的过程为主筛,称带走的
的倍数含量的过程为主筛,称带走的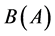 中的数的过程,叫做对
中的数的过程,叫做对 的从筛。
的从筛。
由引理1,引理4可知,筛除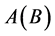 中的素数
中的素数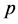 的倍数含量时,不仅按引理1 (重叠比例定理)暗筛
的倍数含量时,不仅按引理1 (重叠比例定理)暗筛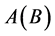 中的
中的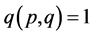 的部分倍数含量,而且又按照引理4 (等差项同数列的性质)从筛了
的部分倍数含量,而且又按照引理4 (等差项同数列的性质)从筛了 中的
中的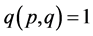 的部分倍数含量。
的部分倍数含量。
5. 两筛法
5.1. 简单比例两筛法
大偶数2n表两数和的式子共有n种,
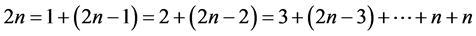 ,
,
前项集合: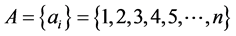 ,
,
后项集合: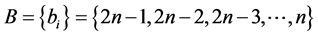 ,
,
两边(前项A,后项B)同时按引理1的推论2及定理4,筛除A,B中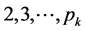 (
( 为小于等于
为小于等于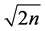 最大素数)的倍数含量,两筛过程:其中2的倍数成对出现,所以只要筛除
最大素数)的倍数含量,两筛过程:其中2的倍数成对出现,所以只要筛除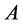 中2的倍数就把
中2的倍数就把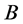 中2的倍数带走了。这样筛2的倍数含量时,只要一次按2的倍数含量的比例
中2的倍数带走了。这样筛2的倍数含量时,只要一次按2的倍数含量的比例 进行筛除即可(其余的是2n倍数的,也都按照两次筛,作为加强了)得
进行筛除即可(其余的是2n倍数的,也都按照两次筛,作为加强了)得
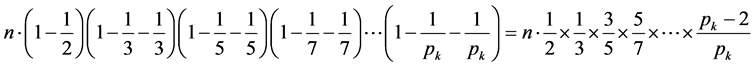
5.2. 加强比例两筛法:
依据引理1的推论2,引理2,引理4,两边(前项A,后项B)同时加强依次筛除A,B中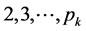 (
(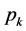 为小于等于
为小于等于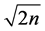 最大素数)的倍数含量,筛除2,3的倍数时,用
最大素数)的倍数含量,筛除2,3的倍数时,用 和
和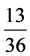 代替原来的2,3的倍数(含量)占有比例
代替原来的2,3的倍数(含量)占有比例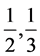 ,在筛除
,在筛除 的倍数时,按照比例
的倍数时,按照比例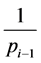 筛除,这种筛除方法我们称之为加强比例两筛法,简称两筛法。
筛除,这种筛除方法我们称之为加强比例两筛法,简称两筛法。
易得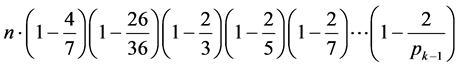
( 的最大素数)
的最大素数)
由此易得,第一个算式:
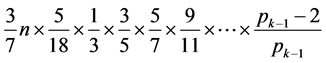
( 的最大素数) (一)
的最大素数) (一)
5.3. 加强比例两筛法的另一应用:
小于n的差为2的数对,共有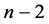 种形式:
种形式:
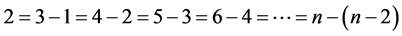
前项集合: ,
,
后项集合: 。
。
两边(前项C,后项D)同时加强筛除C,D中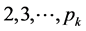 (
( 的最大素数)的倍数含量,筛除2,3的倍数时,用
的最大素数)的倍数含量,筛除2,3的倍数时,用 和
和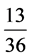 代替原来的2,3的倍数(含量)占有比例
代替原来的2,3的倍数(含量)占有比例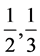 ,在筛除
,在筛除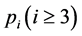 的倍数时,按照比例
的倍数时,按照比例 筛除,则最后至少剩下
筛除,则最后至少剩下

(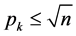 最大素数)。
最大素数)。

( 的最大素数)个式子。
的最大素数)个式子。
所以,小于n的相差为2的素数对

(后边中括号中的每一项都小于1,则乘积小于1)
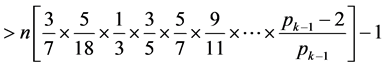
去掉中括号,−1暂且忽略不计,易得,第二个算式:
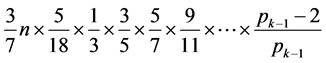
( 最大素数) (二)
最大素数) (二)
5. 恒等式 的妙用
的妙用
恒等式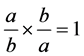 ,看似简单,一个巧妙的应用,却解决了以上两个算式由有限到无限的问题。
,看似简单,一个巧妙的应用,却解决了以上两个算式由有限到无限的问题。
算式(一): 的值(其中
的值(其中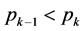 ,
,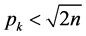 的最大素数),在
的最大素数),在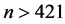 时,其值永远大于2。
时,其值永远大于2。
证明:取 ,
,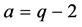 ,(q为合数),巧用
,(q为合数),巧用 ,
,
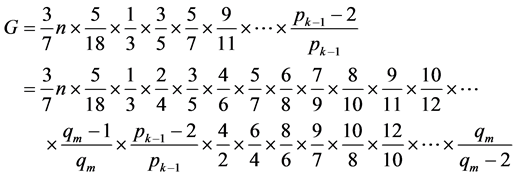
(其中 ,是小于
,是小于 的最大合数),
的最大合数),
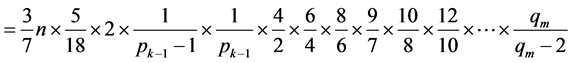
 ,所以
,所以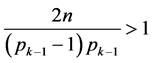 ,用1代替
,用1代替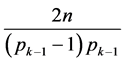 ,
,
从而
经过计算易知,计算到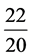 时,其值是2.1471949104后边的每项
时,其值是2.1471949104后边的每项 都大于1。
都大于1。
所以取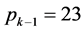 ,为
,为 ,
, 。当
。当 ,
,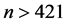 时,其值永远大于2.即
时,其值永远大于2.即 时,
时, ,问题得证。
,问题得证。
即大偶数都能表为两素数之和。
算式(二):
(其中 ,
,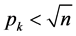 的最大素数),求证:在
的最大素数),求证:在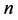 是无穷大时,L的值也一定是无穷大的.
是无穷大时,L的值也一定是无穷大的.
证明:取 ,
, ,(q为合数),巧用
,(q为合数),巧用 。
。

(其中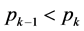 ,
,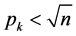 的最大素数)
的最大素数)
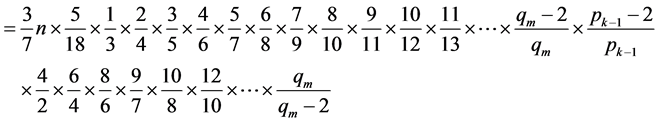
(其中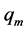 为小于
为小于 的最大合数,即
的最大合数,即 )
)

因为 ,所以
,所以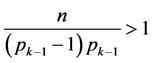 ,用1代替
,用1代替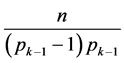
 (二)
(二)
又(二)中的q为偶合数时的,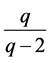 式的连乘积
式的连乘积
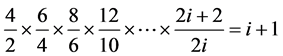
所以, (二)
(二)
在(二)式中 为有限数,
为有限数, ,
,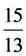 ,
,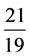 ,……等又都大于1,
,……等又都大于1,
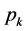 是无穷大的,小于
是无穷大的,小于 的最大偶合数也是无穷大的,那么
的最大偶合数也是无穷大的,那么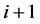 也是无穷大的。
也是无穷大的。
所以其积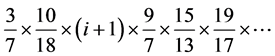 ,也一定是无穷大的,−1也就真的可忽略不计了。
,也一定是无穷大的,−1也就真的可忽略不计了。
即:差为2的素数对有无穷多。
类似的,易证,差为4的素数对也有无穷多。
文章引用
鲁思顺. 倍数含量筛法与恒等式((a/b)×(b/a)=1 )的妙用
Sieve of Multiple Content and Subtle Effects of ((a/b)×(b/a)=1 )[J]. 理论数学, 2017, 07(04): 288-296. http://dx.doi.org/10.12677/PM.2017.74038
参考文献 (References)
- 1. 鲁思顺. 加强含量筛法与哥德巴赫猜想探索[J]. 延安教育学院学报, 2001(2): 48-50.
- 2. 鲁思顺. 加强比例的一种应用[J]. 山东大学学报(理科版), 2012(S1): 9-13.