Advances in Applied Mathematics
Vol.07 No.01(2018), Article ID:23559,9
pages
10.12677/AAM.2018.71012
Semi-Tensor Method for Minimum Energy Consumption Problem in Boolean Control Networks
Liu Qian1, Wei Wei1, Fanqiang Fu1, Ying Zhou2
1School of Data Science and Information Engineering, Guizhou Minzu University, Guiyang Guizhou
2School of Mathematics and Statistics, Guizhou University, Guiyang Guizhou
Received: Dec. 22nd, 2017; accepted: Jan. 18th, 2018; published: Jan. 26th, 2018

ABSTRACT
Boolean network is an important model to study biological systems and gene regulatory networks. In this paper, a new expression of the object functional of the algebraic state space representation and the minimum energy consumption problem of the logical dynamical system is given by using the matrix half tensor product method. Then the dynamic programming method is used to discuss the optimization problem. Finally, an example is given to illustrate the effectiveness of the proposed algorithm.
Keywords:Boolean Network, Semi-Tensor Product, Dynamic Programming, Optimal Control
布尔控制网络最小能耗问题的半张量方法
钱柳1,韦维1,符繁强1,周荧2
1贵州民族大学,数据科学与信息工程学院,贵州 贵阳
2贵州大学,数学与统计学院,贵州 贵阳
收稿日期:2017年12月22日;录用日期:2018年1月18日;发布日期:2018年1月26日

摘 要
布尔网络是研究生物系统和基因调控网络的一种重要模型。本文利用矩阵半张量积的方法,给出逻辑动态系统的代数状态空间表示和最小能耗问题目标泛函的一个新的表达形式,并应用动态规划法求解其最优控制问题,最后举例说明算法的有效性。
关键词 :布尔网络,半张量积,动态规划,最优控制

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
布尔网络是描述人工智能系统、神经网络系统、基因调控网络等的有效工具之一。早在上世纪60年代,Jacob和Monod发现任何细胞的调控基因像开关一样,能打开或关闭其他基因。1969年,Kauffman首次提出用布尔网络描述细胞和基因的调控网络,将基因的表达和不表达分别用逻辑值“1”和“0”表示,基因之间复杂的关系和作用通过简单的逻辑关系表达,这种理想化的模型不仅具有高度抽象性,而且反映了系统丰富的动力学行为。虽然基因的调控网络可用逻辑表达式表示其演化过程,但它不能融入基本数学运算框架,在系统分析及综合时也不方便。2011年,程代展教授提出了矩阵半张量积的概念 [1] ,作为普通矩阵乘法的推广,不再要求前一个矩阵的列数等于后一个矩阵的行数,还保持了普通矩阵乘法的基本性质。利用矩阵半张量积,逻辑动态方程可用矩阵表达成代数形式,进而,可利用控制理论中已有的数学工具和方法,有效地解决逻辑动态系统问题。程代展教授及其团队在专著 [2] [3] [4] 中详细介绍了矩阵半张量积的定义和性质,并讨论其在非线性系统、布尔网络、模糊逻辑等领域中的应用。利用半张量积解决布尔网络问题已有了一些优秀成果,如:逻辑动态系统的拓扑结构,逻辑控制系统的能控性、能观性、稳定性、镇定性、干扰解耦、最优控制等。
布尔网络的最优控制问题也是一个倍受关注的主题,应用半张量积的方法研究最优控制问题也有了一些结果,如文献 [5] [6] 基于网络的环结构,研究了布尔控制网络和多值逻辑控制网络的最优性条件,文献 [7] [8] 研究了单输入和多输入的布尔控制网络的一种Mayer型最优控制问题,文献 [9] 研究了无穷时域概率布尔网络最优控制问题等。在最优控制理论中,最小能量控制是现代控制中最基本、最重要的问题之一。经查阅相关文献,对布尔网络最小能量控制的研究比较少,其原因在于将逻辑形式和代数形式在统一的框架下处理有一定的难度。本文利用半张量积的方法研究布尔网络的最小耗能问题,在将布尔网络的逻辑动态表达式转化为代数状态表达式的基础上,给出目标泛函半张量积的表达形式,利用动态规划方法求解相应的最优控制问题,最后通过具体的算例说明算法的有效性。
2. 预备知识
2.1. 符号说明
·
表示正整数集合。
·
是实数域上
维向量空间。
·
为
实矩阵集合。
·
,其中
为单位矩阵
的第
列,特别地
。
· 矩阵
称为逻辑矩阵,若它的列
,记
为
阶逻辑矩阵集合。
·
,记为
。
· 逻辑变量
,将逻辑值用二维向量表示为
,即逻辑变量
。
2.2. 半张量矩阵的定义及性质
矩阵半张量积是一种新的矩阵乘法,它是普通矩阵乘法的推广,推广后的乘法不仅保持了普通矩阵乘法的主要性质,还具有伪交换性。
定义2.2.1 [3] :设
,记
与
的最小公倍数为
,则矩阵
和
的左半张量积定义为
.
注2.2:当
时,矩阵
满足等维条件,半张量积退化为普通矩阵乘法,
是矩阵的Kronecker积(亦称张量积)。下文所说的半张量积均为左半张量积。
命题2.2.1 [3] :若
,则
满足:
1) 分配律
.
2) 结合律
.
3) 转置
.
为了进一步刻画和应用半张量积,定义如下换位矩阵。
定义2.2.2 [4] :换位矩阵
是一个
的矩阵,它的行和列是由双指标
标注,列是按照索引
排列,行是双指标
标注按照索
排列,并且位于
元素的值为
.
当
,记
。
通过换位矩阵,引入半张量积的重要性质-伪交换性。
命题2.2.2 [4] :1) 设
为列向量,
为矩阵,则
.
2) 设
为行向量,
为矩阵,则
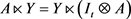 .
.
3) 设两个列向量
,则
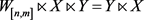 .
.
4) 设两个行向量
,则
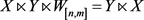 .
.
命题2.2.2使矩阵乘法有了一定的可交换性,称为伪交换性。
3. 布尔控制网络最小能耗问题
布尔网络是一种理想化的模型,用于研究基因调控和细胞分化过程,基因的状态分为表达和不表达,用1和0表示,其网络每个基因之间的相互作用通过布尔函数描述。对于含有
结点和
个控制输入的布尔网络,用
表示取值集合。设
表示第
个结点
时刻基因的状态,
表示
个控制输入,
时刻的基因状态
完全由
时刻各结点的基因状态
按已知的传播机理传播,用布尔函数
来描述,故控制状态方程可以描述为
(1)
其中,
,
;
。令容许控制集为
 。
。
最优控制问题(P):寻找最优控制
,
满足使系统状态从给定的初始状态
在
时刻运行到给定的终端状态
,并使系统的能耗最小,即
(2)
其中,
为
维的正定对称矩阵,为简便,我们这里考虑
为正定的对角矩阵,各对角元的大小表达控制分量的权重。
此最优控制问题既包含了状态系统的逻辑运算,又包含了性能指标中的代数运算。用单一的逻辑网络或一般状态系统的最优控制方法不能处理。为了求解此问题,我们考虑用矩阵半张量积的方法处理,因矩阵半张量积这一工具可以将逻辑动态网络转化为代数状态方程形式。
4. 布尔控制网络最小能耗问题的半张量方法表示及问题的求解
4.1. 半张量积的方法表示布尔控制网络最小能耗问题
为了应用半张量积方法,引入如下定义及引理:
定义4.1.1 [4] :设
是一个行向量,
是一个列向量。
1) 如果
是
的因子,即
,则
维行向量
称为
和
左半张量内积,
,
。
2) 如果
是
的因子,即
,则
维行向量
也称为
和
左半张量内积。
引理4.1.1 [10] :设
是
个逻辑变量,对于任意的
元布尔函数
,存在唯一的逻辑矩阵
,使得
上式称为布尔函数
的代数形式。
根据引理4.1.1、定义4.1.1和半张量矩阵的运算性质,我们可以将问题(P)等价于如下问题:
设
为
个指标按照
的自然索引
时的第
个元素对应的单指标索引。
状态方程
. (3)
初始状态
和终端
给定,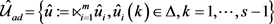 为容许控制集。目标泛函为
为容许控制集。目标泛函为
. (4)
最优控制问题(
):寻找
其中
是状态变量,
是控制变量,
为结构矩阵。
4.2. 最优控制问题的求解
最优控制问题求解常用的方法有变分法、动态规划法和庞特里亚金极大值原理。本文采用动态规划法求解最优控制问题(P)。根据最优性原理,针对半张量积表示的最优控制问题(
),我们得到如下定理。
定理4.2.1 [11] :(最优性原理)对于问题(
),如果
是最优策略,则任意的
,它的子策略
对于由
,
确定的
为起点的第
到
后部分子过程而言,也是最优策略。
下面我们将定理4.2.1的思想,转化为可计算的递归算法。对任意给定
和
,考虑如下受控系统
(5)
其中
,设其性能指标为
(6)
其中,
。
最优控制问题(
)为:对于给定的
和
,对应于系统(5),寻找序列
,使得
达到期待的终端值。即
,且
。
显然,
且
时,问题(
)即为我们需求的最优控制问题(
)。此处我们不考虑不可控问题,假设存在控制序列使状态从
到
,我们定义如下值函数
则可以得到如下定理。
定理4.2.2:对任何的
和
,有
证明:由值函数
的定义知
两端关于序列
取最小泛函
对任何序列
,有
故
证毕。
有了上述递归公式,我们可以使用计算机编程求其解。
4.3. 应用实例
例4.3.1设离散系统的状态方程为
给定初始状态
,终端状态
,性能指标为
其中,
逻辑变量,
控制变量,
,
为2阶的对角阵
,求使性能指标最小的控制序列。
解:将逻辑最优控制问题转化为代数形式:
初始条件
,终端
,性能指标为
其中,
,
为状态变量,
,
为控制变量,
。求使性能指标最小的控制系列
,
,
。
应用动态规划求解
情形1:由状态方程
有,
于是,
,
,此时
。
又由于
,则
于是,
,
,此时
。
由于
,则
于是,
,
,
,由
,因此,此情形不是最优解。
情形2
,
,此时
。
,
,此时
。
又由于
,因此,此情形也不是最优解。
情形3
,
,此时
。
,
,此时
。
,
,
。
又
,因此,所求的最优控制序列为
,
,
,最优轨线为
,
,
,性能指标
。
因为
,所以
,
,
,
,
,
,根据逻辑算子的向量表示,最优控制问题的最优控制序列为
,
,
,同理得到最优轨线为
,
,
,性能指标为
。
注4.3:在工程实践中一般应用计算机编程求解。这一类问题的动态规划法采用”空间换时间”的办法,从后往前将每一步可能的值存储到相应单元中,然后根据初始条件确定其最优解。
5. 总结
本文利用半张量积的方法将逻辑控制系统的最小能耗问题转化为代数状态的表示方法,并给出了相应的能量指标泛函的表达式,进而对这一类问题推到了动态规划方程。
致谢
本文得到国家自然科学基金(NSFC)项目(11261011)的资助。
文章引用
钱 柳,韦 维,符繁强,周 荧. 布尔控制网络最小能耗问题的半张量方法
Semi-Tensor Method for Minimum Energy Consumption Problem in Boolean Control Networks[J]. 应用数学进展, 2018, 07(01): 95-103. http://dx.doi.org/10.12677/AAM.2018.71012
参考文献 (References)
- 1. Cheng, D. (2001) Semi-Tensor Product of Matrices and Its Application to Morgen’s Problem. Science in China, 44, 195-212.
- 2. 程代展, 齐洪胜, 刘挺, 等. 从矩阵半张量积到逻辑控制系统[J]. 中国科学, 2016, 46(10): 1401.
- 3. Cheng, D.Z., Qi, H.S. and Zhao, Y. (2012) An Introduction to Semi-Tensor Product of Matrices and Its Applications. World Scientific Publishing Company, Singapore.
https://doi.org/10.1142/8323
- 4. 程代展, 齐洪胜. 矩阵的半张量-理论与应用[M]. 北京: 科学出版社, 2010: 10.
- 5. Zhao, Y., Li, Z. and Cheng, D. (2011) Optimal Control of Logical Control Networks. IEEE Transactions on Automatic Control, 56, 1766-1776.
https://doi.org/10.1109/TAC.2010.2092290
- 6. Zhao, Y. and Cheng, D. (2010) Optimal Control of Mix-Valued Logical Control Networks. The 29th Chinese Control Conference, Beijing, 29-31 July 2010, 1618-1623.
- 7. Laschov, D. and Margaliot, M. (2011) A Maximum Principle for Single-Input Boolean Control Networks. IEEE Transactions on Automatic Control, 56, 913-9I7.
- 8. Laschov, D. and Margaliot, M. (2013) A Pontryagin Maximum Principle for Multi-Input Boolean Control Networks. http://citeseerx.ist.psu.edu/viewdoc/summary?cid=19245596
- 9. Pal, R., Datta, A. and Dougherty, E.R. (2006) Optimal Infinite-Horizon Control for Probabilistic Boolean Networks. IEEE Transactions on Signal Processing, 54, 2375-2387.
https://doi.org/10.1109/TSP.2006.873740
- 10. Cheng, D.Z., Qi, H. and Li, Z. (2011) Analysis and Control of Boolean Networks: A Semi-Tensor Product Approach. Acta Automatica Sinica, 37, 1352-1356.
https://doi.org/10.1007/978-0-85729-097-7
- 11. 吕显瑞, 黄庆道. 最优控制理论基础[M]. 北京: 科学出版社, 2008: 82-95.
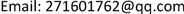





 .
.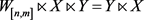 .
.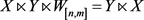 .
. 。
。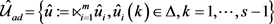 为容许控制集。目标泛函为
为容许控制集。目标泛函为