Advances in Applied Mathematics
Vol.05 No.04(2016), Article ID:19035,11
pages
10.12677/AAM.2016.54079
Blow-Up Criteria for a Kind of Fourth Order Nonlinear Schrödinger Equations
Cailian Mi, Meihong Lu, Han Yang
College of Mathematics, Southwest Jiaotong University, Chengdu Sichuan

Received: Nov. 3rd, 2016; accepted: Nov. 19th, 2016; published: Nov. 24th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The initial-boundary value problem for a kind of fourth order nonlinear Schrödinger equations is studied in this paper. Firstly, with the help of the semi-group theory, the existence and uniqueness of local solution of initial value problem is obtained. Secondly, a new global existence criterion for the classical solution is given by using B-G inequality, namely, that whether the solution globally exists is determined by whether its H2 norm blows up.
Keywords:Nonlinear Schrödinger Equation, Initial Value Problem, B-G Type Inequality, Global Solution, Blow-Up Criteria

一类四阶非线性Schrödinger方程的爆破准则
米彩莲,卢美虹,杨晗
西南交通大学数学学院,四川 成都

收稿日期:2016年11月3日;录用日期:2016年11月19日;发布日期:2016年11月24日

摘 要
本文通过改进的B-G型不等式研究了一类四阶非线性Schrödinger方程的初边值问题。首先借助半群理论得到初值问题局部解的存在唯一性,其次利用B-G型不等式得到了初值问题经典解整体存在的一个新判定准则,即整体解是否存在可由其H2范数是否爆破决定。
关键词 :非线性Schrödinger方程,初值问题,B-G型不等式,整体解,爆破准则

1. 引言
本文考虑如下四阶非线性Schrödinger方程的初边值问题
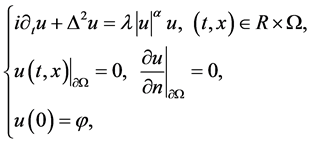 (1.1)
(1.1)
其中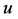 是复值函数,
是复值函数,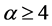 为常数,
为常数,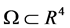 为边界充分光滑的有界区域。问题(1.1)描述的是在Kerr非线性介质中强激光束的稳定孤子的传播模型,其中
为边界充分光滑的有界区域。问题(1.1)描述的是在Kerr非线性介质中强激光束的稳定孤子的传播模型,其中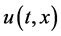 为波函数。方程(1.1)有如下守恒律
为波函数。方程(1.1)有如下守恒律
质量守恒
 , (1.2)
, (1.2)
能量守恒
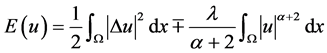 . (1.3)
. (1.3)
首先回顾经典Schrödinger方程的一些研究结果。Brézis和Gallouët [1] 研究了如下的二阶三次非线性Schrödinger方程
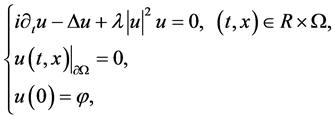 (1.4)
(1.4)
的初边值问题,其中 。该文借助半群理论、能量估计及B-G型不等式
。该文借助半群理论、能量估计及B-G型不等式
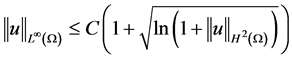 ,
, 且
且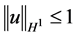 , (1.5)
, (1.5)
建立了解的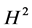 范数的先验估计,得到初边值问题(1.4)经典解的整体存在性。事实上,B-G型不等式(1.5)是对经典的Sobolev不等式的改进,即由把线性增长控制减弱为由对数增长控制,这是该文的主要创新点。
范数的先验估计,得到初边值问题(1.4)经典解的整体存在性。事实上,B-G型不等式(1.5)是对经典的Sobolev不等式的改进,即由把线性增长控制减弱为由对数增长控制,这是该文的主要创新点。
Tsutsumi [2] 考虑了更一般的非线性Schrödinger方程
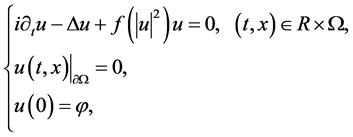 (1.6)
(1.6)
的初边值问题,其中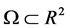 ,对初始条件
,对初始条件 加以更多限制,即要求
加以更多限制,即要求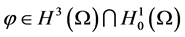 ,
,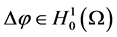 。
。
作者考虑了 的情形,运用衰减估计、Strichartz不等式及B-G型不等式,得到当
的情形,运用衰减估计、Strichartz不等式及B-G型不等式,得到当 时,
时, ,方程(1.6)存在唯一整体解
,方程(1.6)存在唯一整体解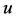 ,即
,即 ,使得
,使得
 ,
,
和
 。
。
最近,Ozawa和Visciglia [3] 研究了如下半波方程的初值问题
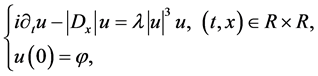 (1.7)
(1.7)
其中 ,建立了如下的B-G型不等式
,建立了如下的B-G型不等式
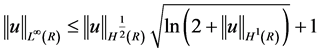 ,
, , (1.8)
, (1.8)
引入能量泛函,运用Yosida正则化准则得到相应的能量估计,进而得到方程(1.7)存在唯一解 ,且得到一个新的爆破准则,即
,且得到一个新的爆破准则,即
i) 当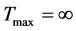 时,整体解存在;
时,整体解存在;
ii) 当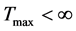 ,且
,且 时,解爆破。
时,解爆破。
文 [3] 还研究了如下的二阶四次非线性Schrödinger方程的初边值问题
 (1.9)
(1.9)
其中 。作者建立了如下的B-G型不等式
。作者建立了如下的B-G型不等式
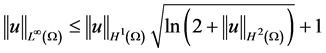 ,
,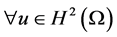 , (1.10)
, (1.10)
得到方程(1.9)存在唯一解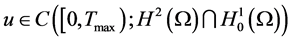 ,且得到一个新的爆破准则,即
,且得到一个新的爆破准则,即
i) 当 时,整体解存在;
时,整体解存在;
ii) 当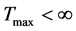 ,且
,且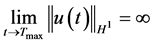 时,解爆破。
时,解爆破。
在空间 、
、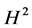 中分别判定问题(1.7)、(1.9)的整体解的存在性,通常是考查其
中分别判定问题(1.7)、(1.9)的整体解的存在性,通常是考查其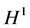 、
、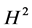 范数的有界性,而该文判定整体解是否存在只需分别考查其
范数的有界性,而该文判定整体解是否存在只需分别考查其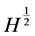 、
、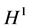 范数是否有界即可,这是该文的创新之处。
范数是否有界即可,这是该文的创新之处。
对于四阶非线性Schrödinger方程情形,Karpman和Shagalov [4] 考虑了如下方程的初值问题
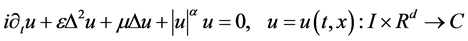 , (1.11)
, (1.11)
其中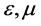 为参数,且
为参数,且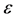 充分小,
充分小, 为空间维数。在文 [4] 中分别给出稳定孤子在一维、二维和三维的存在性和稳定性的条件。Zhu,Yang和Zhang [5] 考虑了如下的四阶非线性Schrödinger方程的初值问题
为空间维数。在文 [4] 中分别给出稳定孤子在一维、二维和三维的存在性和稳定性的条件。Zhu,Yang和Zhang [5] 考虑了如下的四阶非线性Schrödinger方程的初值问题
 , (1.12)
, (1.12)
研究了低正则性解的爆破问题,即考查初值在低正则能量空间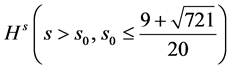 的情形。
的情形。
上述文献没有给出解的爆破准则。本文希望利用文 [3] 的技巧研究方程(1.1),借助半群理论及Segel定理,得到初值问题局部解的存在唯一性,并且通过建立一个B-G型不等式,得到初值问题经典解整体存在的一个新爆破准则。
本文主要结论如下:
定理1.1 假设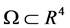 为边界充分光滑的有界区域,
为边界充分光滑的有界区域,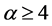 为常数,并记
为常数,并记 ,
,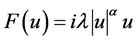 ,
,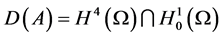 ,则对
,则对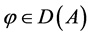 ,方程(1.1)存在唯一经典解
,方程(1.1)存在唯一经典解 ,即
,即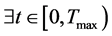 ,使得
,使得
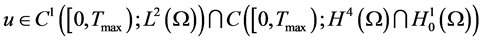 。
。
且有如下的二则性原理
i) 当 时,整体解存在;
时,整体解存在;
ii) 当 ,且
,且 时,解爆破。
时,解爆破。
注:一般情况下判定解是否整体存在要考查其 范数是否有界,本文拟对其改进,建立如下的爆破准则。
范数是否有界,本文拟对其改进,建立如下的爆破准则。
定理1.2 假设在定理1.1的条件下,存在如下二则性原理
i) 当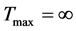 时,整体解存在;
时,整体解存在;
ii) 当 ,且
,且 时,解爆破。
时,解爆破。
注:由定理1.2知,判定方程(1.1)的解是否整体存在只需考虑其 范数是否爆破,而在通常情况下判定解是否整体存在要考查其
范数是否爆破,而在通常情况下判定解是否整体存在要考查其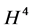 范数是否有界,这是本文的创新。
范数是否有界,这是本文的创新。
本文的安排如下:首先在第一节中介绍背景知识及给出定理1.1和定理1.2;B-G型不等式的构建及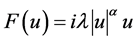 在空间
在空间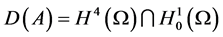 上具有局部Lipschitz连续的证明将在第二节给出;最后定理1.1及定理1.2的证明在第三节给出,通过引入合适的能量泛函,建立解的
上具有局部Lipschitz连续的证明将在第二节给出;最后定理1.1及定理1.2的证明在第三节给出,通过引入合适的能量泛函,建立解的 范数估计。
范数估计。
2. 准备工作
类似文献 [3] ,我们首先构建一个B-G型不等式。
引理2.1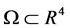 具有光滑边界的有界域,对
具有光滑边界的有界域,对 成立
成立
 , (2.1)
, (2.1)
证 存在延拓算子P: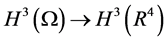 ,且满足
,且满足
P是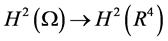 的有界算子,
的有界算子,
P是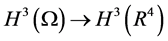 的有界算子,
的有界算子,
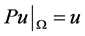 ,
, ,
,
令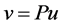 ,
, 记为
记为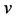 的Fourier变换,易知
的Fourier变换,易知
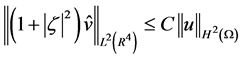 , (2.2)
, (2.2)
 , (2.3)
, (2.3)
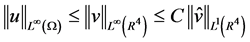 , (2.4)
, (2.4)
对 ,则有
,则有
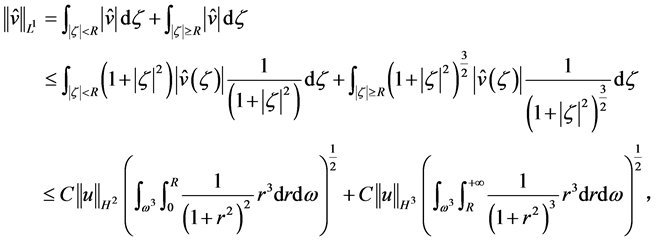
其中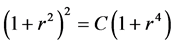 ,上式可得
,上式可得
 (2.5)
(2.5)
此处用到这个事实:当常数 时,得到
时,得到 成立,结合(2.4)及(2.5)式,此处取
成立,结合(2.4)及(2.5)式,此处取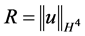 ,因此
,因此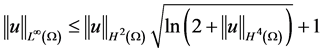 。证毕。
。证毕。
引理2.2 记 ,
,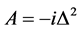 ,
,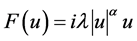 ,则
,则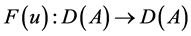 具有局部Lipschitz连续。
具有局部Lipschitz连续。
证 i)易证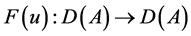 ,
,
ii)下证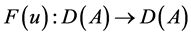 具有局部Lipschitz连续。
具有局部Lipschitz连续。
 (2.6)
(2.6)
只需对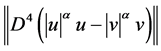 做如下估计
做如下估计
 (2.7)
(2.7)
下面分别对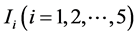 做估计。
做估计。
根据Sobolev嵌入定理
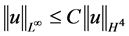 , (2.8)
, (2.8)
及
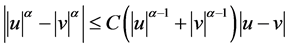 ,(2.9)
,(2.9)
对第一项 进行如下估计
进行如下估计
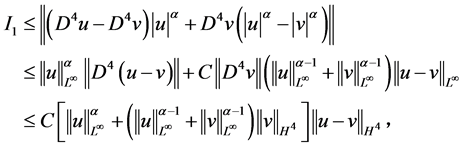
对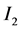 做估计
做估计
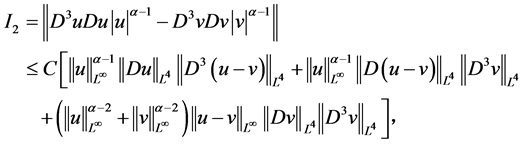 (2.10)
(2.10)
把Sobolev嵌入不等式
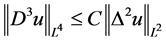 , (2.11)
, (2.11)
及Gagliardo-Nirenberg不等式
 , (2.12)
, (2.12)
代入(2.10)得
 。
。
对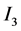 进行估计
进行估计
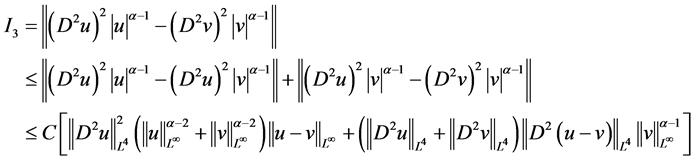 ,
,
由Sobolev嵌入不等式
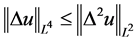 , (2.13)
, (2.13)
及(2.8)式得
 .
.
对 进行估计
进行估计
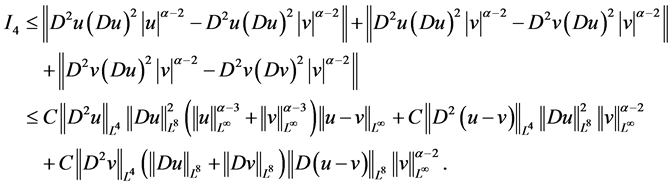
由Gagliardo-Nirenberg不等式
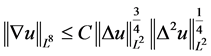 , (2.14)
, (2.14)
Poincaré不等
 , (2.15)
, (2.15)
及(2.8),(2.13)式得
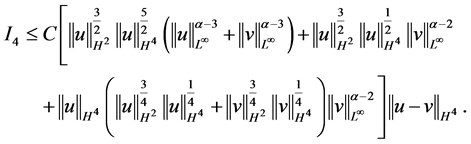
运用(2.8),(2.13)及(2.15)式,对最后一项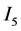 进行估计
进行估计
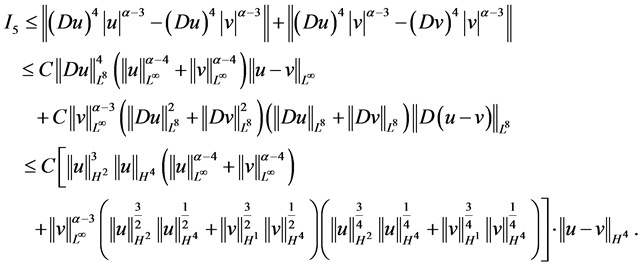
基于 的估计,得
的估计,得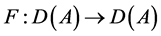 具有局部Lipschitz有界。证毕。
具有局部Lipschitz有界。证毕。
3. 主要结论的证明
下面分别对定理证明。
3.1. 定理1.1的证明
证 由于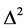 为自伴的m-增值算子,又根据引理2.2得
为自伴的m-增值算子,又根据引理2.2得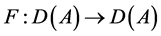 具有局部Lipschitz连续,则由segel定理 [6] ,可得定理1.1成立,证毕。
具有局部Lipschitz连续,则由segel定理 [6] ,可得定理1.1成立,证毕。
3.2. 定理1.2的证明
事实上,我们只需证明 有界可推出
有界可推出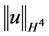 有界。
有界。
首先引入下列能量泛函
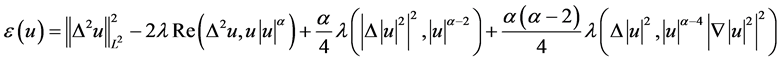 ,
,
引理3.2.1在定理1.1的条件下,则有如下等式
 (3.1)
(3.1)
证 由(1.2)式,则有
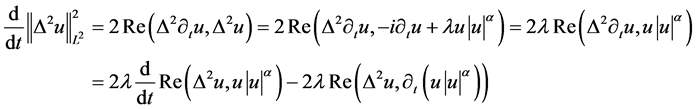 (3.2)
(3.2)
把(3.2)式中第二项变为
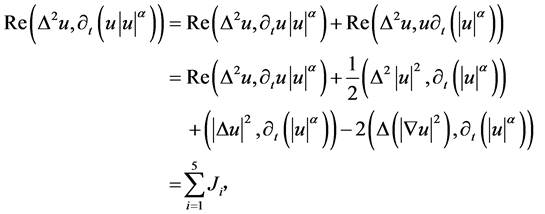
其中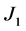 经计算得
经计算得
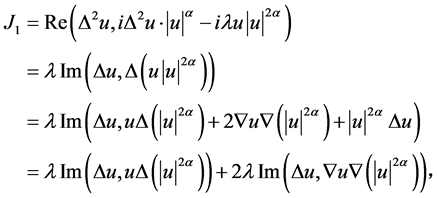
对于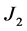 的计算如下
的计算如下
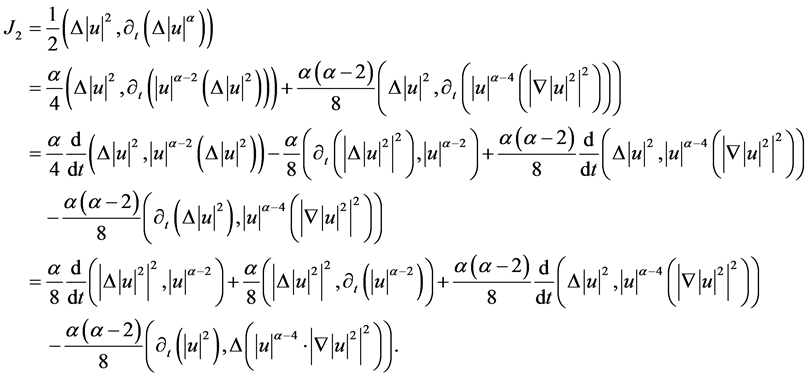
此处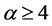 为常数。
为常数。
引理3.2.2在定理1.1的条件下,且 ,得
,得
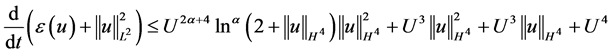 , (3.3)
, (3.3)
证 由引理3.2.1,可知
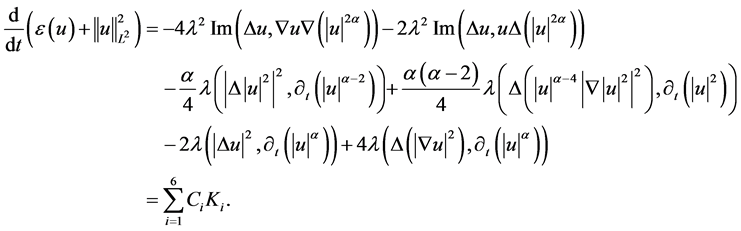
下面分别给出 的估计,其中第一项估计为
的估计,其中第一项估计为
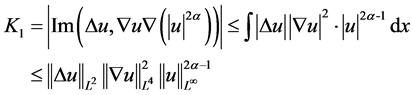
由(2.12)式即得
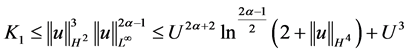 ,
,
同理,对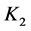 做估计
做估计
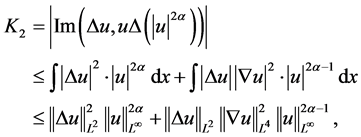
由(2.12)式得到
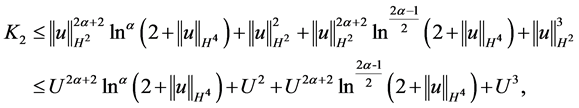
利用不等式 ,对
,对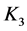 做估计有
做估计有
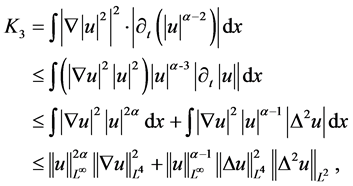
由Gagliardo-Nirenberg不等式
 ,(3.4)
,(3.4)
及(2.12)得到
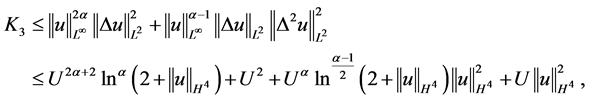
对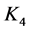 进行估计
进行估计
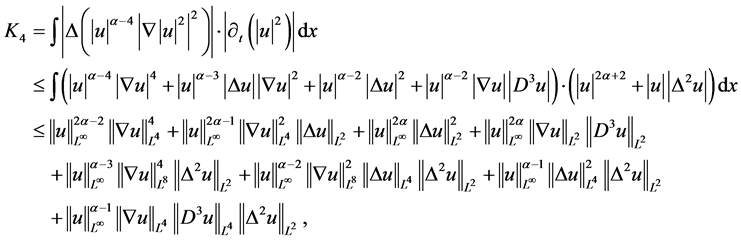
由(2.12),(2.13)及(3.4)式,即对于上式第5项估计
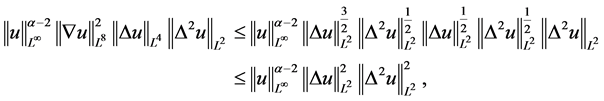
可得
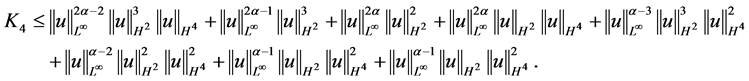
下面对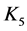 进行估计
进行估计
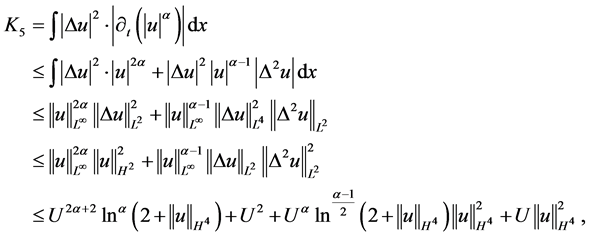
对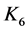 进行估计,同理,即有
进行估计,同理,即有
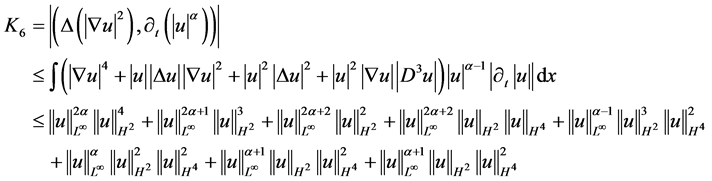
从而引理3.2.2得证。
定理1.2的证明
首先假设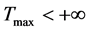 ,且
,且 ,由引理3.2.1,需要对下面几个进行估计,运用Hölder不等式及加权的Young不等式得
,由引理3.2.1,需要对下面几个进行估计,运用Hölder不等式及加权的Young不等式得
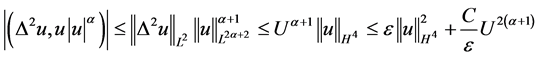 , (3.5)
, (3.5)
利用加权的Young不等式得
 (3.6)
(3.6)
同理,则有
 (3.7)
(3.7)
又由能量泛函 的定义及(3.5)~(3.7)式有
的定义及(3.5)~(3.7)式有
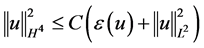 , (3.8)
, (3.8)
再结合(3.3)式和(3.8)式有
 (3.9)
(3.9)
由Gronwall不等式得 ,从而得出矛盾,并结合定理1.1,进而得出结论,证毕。
,从而得出矛盾,并结合定理1.1,进而得出结论,证毕。
文章引用
米彩莲,卢美虹,杨晗. 一类四阶非线性Schro¨dinger方程的爆破准则
Blow-Up Criteria for a Kind of Fourth Order Nonlinear Schro¨dinger Equations[J]. 应用数学进展, 2016, 05(04): 672-682. http://dx.doi.org/10.12677/AAM.2016.54079
参考文献 (References)
- 1. Brézis, H. and Gallouët, T. (1980) Nonlinear Schrödinger Evolution Equations. Nonlinear Analysis: Theory, Methods and Applications, 4, 677-681. https:/doi.org/10.1016/0362-546X(80)90068-1
- 2. Tsutsumi, M. (1989) On Smooth Solutions to the Initial-Boundary Value Problem for the Nonlinear Schrödinger Equation in Two Space Dimensions. Nonlinear Analysis: Theory, Methods and Applications, 13, 1051-1056. https:/doi.org/10.1016/0362-546X(89)90094-1
- 3. Ozawa, T. and Visciglia, N. (2015) An Improvement on the Brézis-Gallouët Technique for 2D NLS and 1D Half-Wave Equation. Annales de l’Institut Henri Poincare (C) Non Linear Analysis, 33, 1069-1079.
- 4. Karpman, V.I. and Shagalov, A.G. (2000) Stability of Solitons Described by Nonlinear Schrödinger-Type Equations with Higher-Order Dispersion. Physica D: Nonlinear Phenomena, 144, 194-210. https:/doi.org/10.1016/S0167-2789(00)00078-6
- 5. Zhu, S., Yang, H. and Zhang, J. (2011) Blow-Up of Rough Solutions to the Fourth-Order Nonlinear Schrödinger Equation. Nonlinear Analysis: Theory, Methods and Applications, 74, 6186-6201. https:/doi.org/10.1016/j.na.2011.05.096
- 6. Zheng, S.M. (2004) Nonlinear Evolution Equations. Chapman & Hall/CRC, London, 56-57. https:/doi.org/10.1201/9780203492222