Advances in Applied Mathematics
Vol.04 No.02(2015), Article ID:15309,7
pages
10.12677/AAM.2015.42024
Cavity Reconstruction Algorithm Based on Electrical Impedance Tomography
Tianhong Feng
School of Mathematics, Dongbei University of Finance & Economics, Dalian Liaoning
Email: fength1212@163.com
Received: May 7th, 2015; accepted: May 22nd, 2015; published: May 27th, 2015
Copyright © 2015 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Electrical impedance tomography problem refers to the imaging of electrical parameters inside the object by measuring the current and voltage value of object surfaces [1] -[3] . An algorithm is proposed aiming at the reconstruction of homogeneous medium in the electrical impedance tomography with cavity. The basic idea of the algorithm is using analytic continuation to transfer the original problem to the Cauchy problem of circle domain; Newton-type iterative method is used to solve the nonlinear equations, getting the assemblage whose normal derivative is zero satisfying the solution of Cauchy problem, and then the boundary of the cavity is gotten. At the same time, numerical examples of several kinds of special shaped cavity reconstruction are presented to demonstrate the feasibility of this algorithm.
Keywords:Electrical Impedance Tomography, Cauchy Problem, Newton-Type Iterative Method
基于电阻抗成像问题的空腔重构算法
凤天宏
东北财经大学数学学院,辽宁 大连
Email: fength1212@163.com
收稿日期:2015年5月7日;录用日期:2015年5月22日;发布日期:2015年5月27日

摘 要
电阻抗成像问题是通过测量物体表面的电流和电压值,来对物体内部的电参数进行成像[1] -[3] 。本文针对电阻抗成像中带有空腔的均匀介质的重构给出一种算法。算法的基本思想是利用解析延拓,将原问题转化为圆环域上的Cauchy问题,然后利用Newton迭代法求解此非线性方程组,得到Cauchy问题的解所满足的法向导数为零的集合,进而得到空腔的边界。同时给出几种特殊形状空腔重构的数值算例来说明算法的可行性。
关键词 :电阻抗成像,Cauchy问题,Newton迭代法

1. 问题的描述
考虑圆形域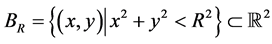 ,边界为
,边界为 。
。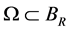 为包含原点的有界单连通区域(空腔),边界为
为包含原点的有界单连通区域(空腔),边界为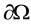 ,满足
,满足 ,并且存在常数
,并且存在常数 ,满足
,满足 。设
。设 和
和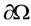 充分光滑,
充分光滑,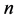 表示相应于
表示相应于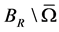 的单位外法向量。
的单位外法向量。
于边界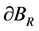 处注入电流
处注入电流

并测量边界电势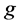 ,假设测量精确,则电势
,假设测量精确,则电势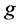 满足
满足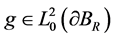 ,并且
,并且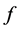 与
与 之间满足DtN映射:
之间满足DtN映射:
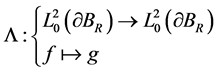
于是电位势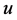 满足Laplace方程
满足Laplace方程
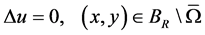 (1.1)
(1.1)
及边界条件
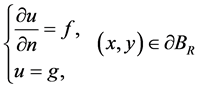 (1.2)
(1.2)
 (1.3)
(1.3)
则Cauchy问题(1.1)和(1.2)存在唯一解
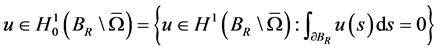
我们的问题是由(1.1)、(1.2)和(1.3)式得到空腔 的形状,即确定
的形状,即确定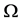 的边界
的边界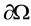 [4] 。
[4] 。
2. 数学模型的建立
我们考虑极坐标变换
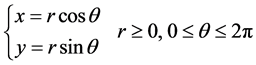
设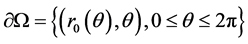 ,于是(1.1)和(1.2)式转化为极坐标系下的Cauchy问题:
,于是(1.1)和(1.2)式转化为极坐标系下的Cauchy问题:
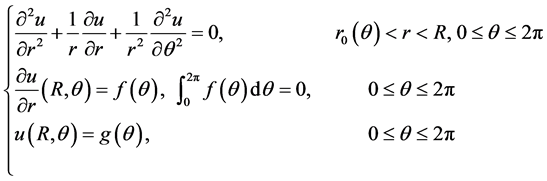 (2.1)
(2.1)
并满足周期条件
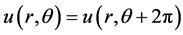 (2.2)
(2.2)
另一方面,在直角坐标系下,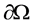 上的单位切向量为
上的单位切向量为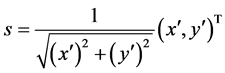 ,由
,由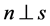 知,
知,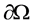 上的单位外法向量为
上的单位外法向量为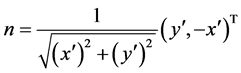 ,再根据极坐标变换有
,再根据极坐标变换有
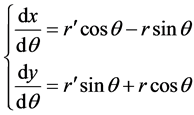
于是有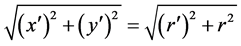 ,从而可得
,从而可得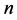 在极坐标系下表示为
在极坐标系下表示为

从而内区域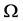 上的边界条件(1.3)转化为
上的边界条件(1.3)转化为
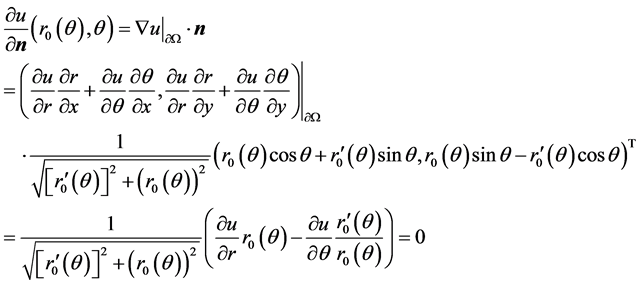
即
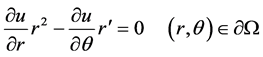 (2.3)
(2.3)
从而我们的问题可描述为:求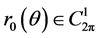 ,满足
,满足
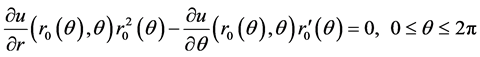 (2.4)
(2.4)
其中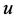 是方程(2.1)的解。
是方程(2.1)的解。
由 满足的条件知,存在常数
满足的条件知,存在常数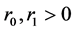 ,满足
,满足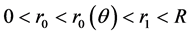 。于是在极坐标系下设
。于是在极坐标系下设
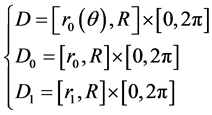
满足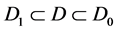 。
。
考虑下述Cauchy问题:
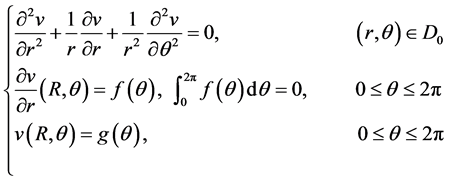 (2.5)
(2.5)
并满足周期条件
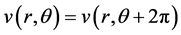 (2.6)
(2.6)
由解析延拓的性质[5] 知,Cauchy问题(2.1)和(2.5)的解于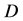 中相等,即
中相等,即 。
。
下面,我们利用分离变量法解Cauchy问题(2.5),得到其解的解析表达式之后寻找该解于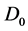 中法向导数为零的点集,从而得到
中法向导数为零的点集,从而得到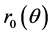 的表达式,进而得到空腔
的表达式,进而得到空腔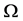 的边界。
的边界。
首先,令 ,带入(2.5)式方程可得
,带入(2.5)式方程可得
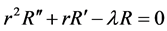 (2.7)
(2.7)
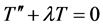 (2.8)
(2.8)
由周期条件(2.2)知
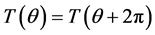 (2.9)
(2.9)
(2.8)和(2.9)式构成特征值问题,显然其特征值和特征函数分别为
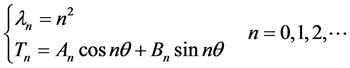
其中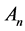 和
和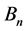 为实数。将特征值
为实数。将特征值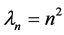 带入(2.7)式,得齐次欧拉方程:
带入(2.7)式,得齐次欧拉方程:

其解为
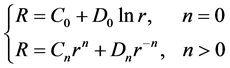
所以,Cauchy问题(2.5)的解的一般形式为
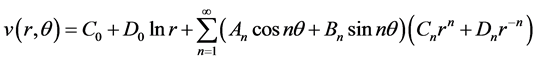 (2.10)
(2.10)
为确定上式的叠加系数,将(2.5)中的边界条件写成下列级数形式:
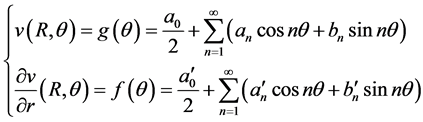 (2.11)
(2.11)
其中 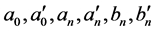 已知。由(2.10)式知
已知。由(2.10)式知
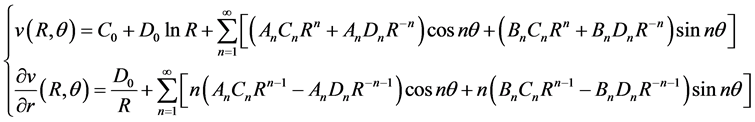 (2.12)
(2.12)
比较(2.11)式和(2.12)式的系数,分别得到
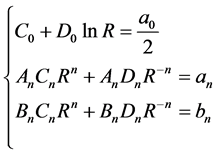 和
和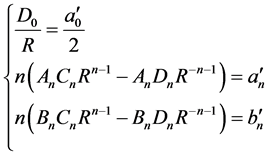
由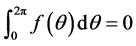 ,有
,有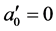 ,从而
,从而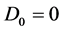 ,
,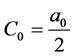 ,进而可得
,进而可得
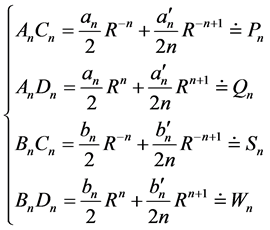
于是Cauchy问题(2.5)的解(2.10)式可写成:
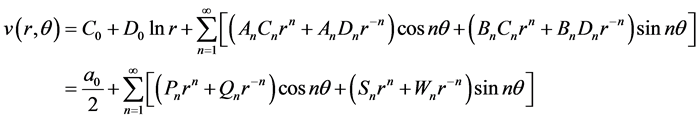
其中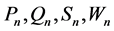 已知。进一步有
已知。进一步有
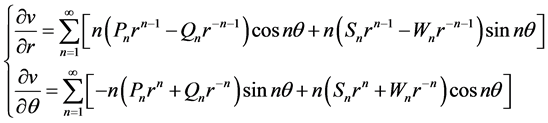
则
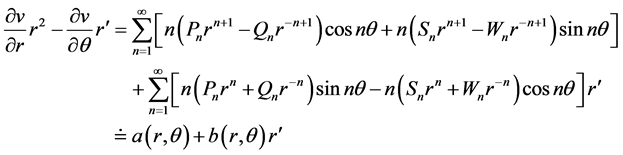 (2.13)
(2.13)
其中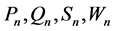 已知。于是问题(2.4)可描述为:求
已知。于是问题(2.4)可描述为:求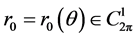 ,满足
,满足
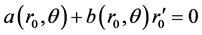 (2.14)
(2.14)
3. 重构算法
我们基于求解非线性算子方程的Newton迭代法思想,给出求解问题(2.14)的迭代算法。对于非线性方程
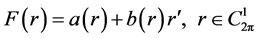 (3.1)
(3.1)
设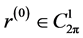 为给定的初始近似,对于
为给定的初始近似,对于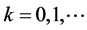 ,做迭代
,做迭代
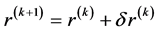 (3.2)
(3.2)
直至 收敛,其中
收敛,其中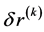 是线性问题
是线性问题
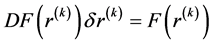 (3.3)
(3.3)
的解。此处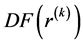 是非线性算子
是非线性算子 于
于 处的Fréchet导数。
处的Fréchet导数。
以上算法的关键步骤是当给定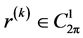 后,如何求得
后,如何求得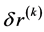 。为此,我们考虑如下问题:给定函数
。为此,我们考虑如下问题:给定函数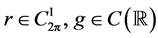 ,求
,求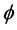 ,满足
,满足
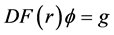 (3.4)
(3.4)
首先由(3.1)式以及Taylor公式可得

于是对于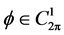 ,(3.4)式为
,(3.4)式为
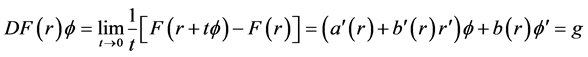 (3.5)
(3.5)
其中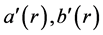 可由(2.13)式中
可由(2.13)式中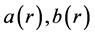 的表达式得到
的表达式得到
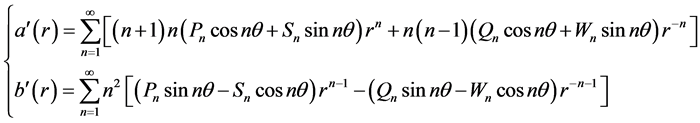
为求解(3.5)式,对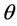 进行均匀剖分
进行均匀剖分 ,剖分步长为
,剖分步长为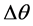 ,设
,设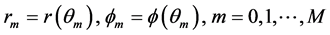 ,将差分格式
,将差分格式
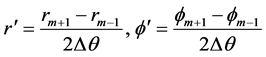 (3.6)
(3.6)
代入(3.5)式,解线性方程组
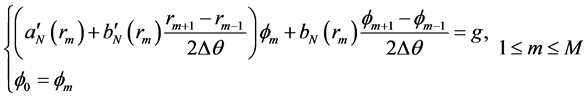 (3.7)
(3.7)
其中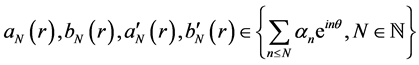 。
。
于是我们得到问题(3.4)的解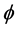 ,即当给定
,即当给定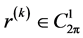 时,通过上述过程得到
时,通过上述过程得到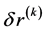 ,代回(3.2)式,依次类推。当
,代回(3.2)式,依次类推。当 时,迭代停止。
时,迭代停止。
4. 数值实验
我们分别对介质内部三种不同形状的空腔进行重构,来说明重构算法的可行性。三个空腔均为星型域,图1的空腔具有风筝形状,其边界参数方程为

图2的空腔具有花生形状,其边界参数方程为
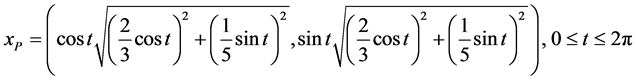
图3的空腔边界为分段光滑,其参数方程为
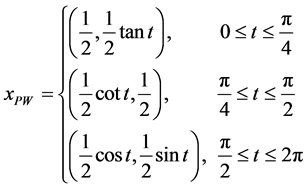
算法的初始迭代曲线为中心在原点,半径为0.5的圆,算法的收敛准则为自变量和泛函值连续迭代误差小于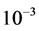 。对于输入数据
。对于输入数据 含噪音的情况,我们按下述方式添加噪音模拟“测量”数据
含噪音的情况,我们按下述方式添加噪音模拟“测量”数据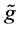 :
:
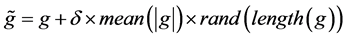
这里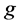 表示在剖分节点上的真实值组成的向量,其中
表示在剖分节点上的真实值组成的向量,其中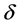 为噪音水平,
为噪音水平,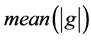 表示
表示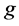 绝对值的平均值,
绝对值的平均值,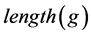 表示
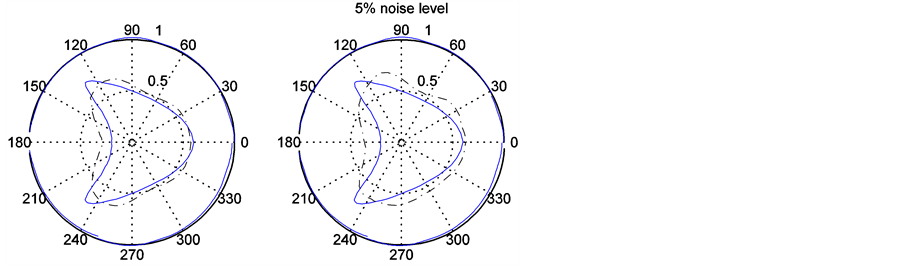
表示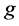 的维数,
的维数, 是一个
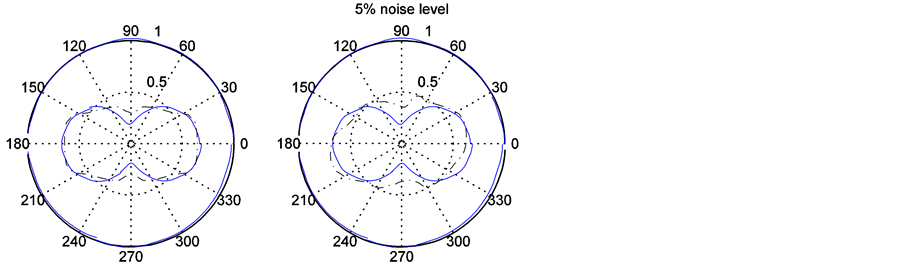
是一个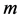 维随机向量[6] 。
维随机向量[6] 。
图1(a)、图2(a)和图3(a)是在假定边界输入数据精确的情形下,三种空腔的重构效果;图1(b)、图2(b)和图3(b)分别表示输入数据含5%噪声水平的空腔重构效果。
 (a)(b)
(a)(b)
Figure 1. (a) Reconstruction of kite shape cavity; (b) Reconstruction with noise data
图1. (a) 风筝形状空腔重构;(b) 带有噪声数据的重构
 (a)(b)
(a)(b)
Figure 2. (a) Reconstruction of peanut shape cavity; (b) Reconstruction with noise data
图2. (a) 花生形状空腔重构;(b) 带有噪声数据的重构
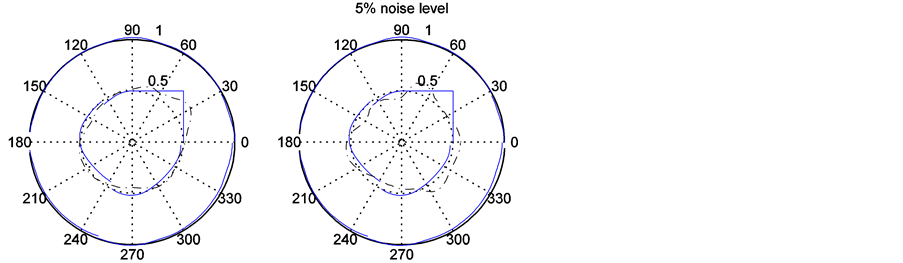 (a)(b)
(a)(b)
Figure 3. (a) Reconstruction of piecewise smooth cavity; (b) Reconstruction with noise data
图3. (a) 边界分片光滑空腔重构;(b) 带有噪声数据的重构
5. 总结
本文基于电阻抗成像,针对带有空腔的均匀介质的重构问题,利用解析延拓以及求解非线性方程的Newton法的思想,给出了一种迭代算法,并针对几种特殊的空腔形状给出了算例。实验结果表明,该算法比较稳定,相对误差较小,但计算量和存储量比较大,并且对于空腔位置有一定要求。如何提高带有尖角的空腔的重构质量,是我们下一步研究的重点。
基金项目
辽宁省教育厅科学研究一般项目(No. L2014457);东北财经大学青年基金培育项目(No. DUFE2014Q64)。
文章引用
凤天宏, (2015) 基于电阻抗成像问题的空腔重构算法
Cavity Reconstruction Algorithm Based on Electrical Impedance Tomography. 应用数学进展,02,189-196. doi: 10.12677/AAM.2015.42024
参考文献 (References)
- 1. Borcea, L. (2002) Electrical impedance tomography. Inverse Problems, 18, 99-136.
- 2. Brühl, M. and Hanke, M. (2003) Recent progress in electrical impedance tomography. Inverse Problems, 19, S65-S90.
- 3. Holder, D. (2005) Electrical impedance tomography. Institute of Physics Publishing, Bristol and Philadelphia.
- 4. Isakov, V. (1998) Inverse problem for partial differential equations. Springer-Verlag, New York.
- 5. Qian, Z., Fu, C.L. and Xiong, X.T. (2006) Fourth-order modified method for the Cauchy problem for the Laplace equation. Journal of Computational and Applied Mathematics, 192, 205-218.
- 6. Nocedal, J. and Wright, S.J. (1999) Numerical optimization. Springer, Ber-lin.