Advances in Applied Mathematics
Vol.05 No.03(2016), Article ID:18438,8
pages
10.12677/AAM.2016.53054
On the Anti-Forcing Number of 
Yongjun Zhang, Jinzhuan Cai*
Department of Mathematics, Hainan University, Haikou Hainan

Received: Aug. 15th, 2016; accepted: Aug. 27th, 2016; published: Aug. 30th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Let G be a simple connected graph with a perfect matching, S an edge set of G. We call S an anti- forcing set of G, if  contains only one perfect matching of G. The cardinality of the minimum anti-forcing set of G is called the anti-forcing number of G. In this paper, we study the anti-forcing number of the Cartesian product of a cycle and a path. According to the necessity of a graph with only one perfect matching, we show that the anti-forcing numbers of
contains only one perfect matching of G. The cardinality of the minimum anti-forcing set of G is called the anti-forcing number of G. In this paper, we study the anti-forcing number of the Cartesian product of a cycle and a path. According to the necessity of a graph with only one perfect matching, we show that the anti-forcing numbers of  are all
are all , and the anti-forcing number of
, and the anti-forcing number of  is 3.
is 3.
Keywords:The Cartesian Product of a Cycle and a Path, Perfect Matching, Anti-Forcing Numbers

关于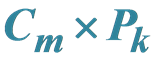 的反强迫数
的反强迫数
张勇军,蔡金转*
海南大学数学系,海南 海口

收稿日期:2016年8月15日;录用日期:2016年8月27日;发布日期:2016年8月30日

摘 要
设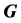 是一个有完美匹配的简单连通图。若
是一个有完美匹配的简单连通图。若 的一个边子集
的一个边子集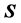 满足
满足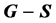 只有唯一完美匹配,则称
只有唯一完美匹配,则称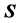 是
是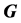 的一个反强迫集。
的一个反强迫集。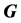 中最小的反强迫集的大小称为
中最小的反强迫集的大小称为 的反强迫数。本文主要研究圈和路的卡什积图的反强迫数。根据一个图有唯一完美匹配的必要条件,我们证明了
的反强迫数。本文主要研究圈和路的卡什积图的反强迫数。根据一个图有唯一完美匹配的必要条件,我们证明了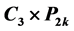 ,
,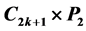 ,
,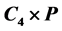 的反强迫数都为
的反强迫数都为 ,并表明了
,并表明了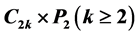 的反强迫数恒为3。
的反强迫数恒为3。
关键词 :圈和路的卡什积图,完美匹配,反强迫数

1. 引言
图 的完美匹配
的完美匹配 是指覆盖了
是指覆盖了 的所有顶点的一个独立边集,它对应于化学中的凯库勒结构。Randic和Klein对凯库勒结构提出了内自由度的概念 [1] [2] ,图的完美匹配对应地也有强迫数这一概念 [3] 。一个边集
的所有顶点的一个独立边集,它对应于化学中的凯库勒结构。Randic和Klein对凯库勒结构提出了内自由度的概念 [1] [2] ,图的完美匹配对应地也有强迫数这一概念 [3] 。一个边集 称为图
称为图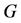 的完美匹配
的完美匹配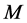 的强迫集是指
的强迫集是指 只包含在
只包含在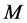 中,但不包含在其它完美匹配中。
中,但不包含在其它完美匹配中。 的最小的强迫集的大小称为
的最小的强迫集的大小称为 的强迫数。近年来,化学图论专家针对图的完美匹配又陆续提出了强迫六角形,全局强迫数,反凯库勒数和反强迫数等概念。其中,反强迫数的概念最早是由Vukicevic和Trinajstic提出来的 [4] 。
的强迫数。近年来,化学图论专家针对图的完美匹配又陆续提出了强迫六角形,全局强迫数,反凯库勒数和反强迫数等概念。其中,反强迫数的概念最早是由Vukicevic和Trinajstic提出来的 [4] 。
若图 一个边集
一个边集 满足
满足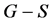 只有唯一完美匹配,则称
只有唯一完美匹配,则称 为图
为图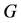 的反强迫集。图
的反强迫集。图 最小的反强迫集的大小称为
最小的反强迫集的大小称为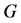 的反强迫数,并用
的反强迫数,并用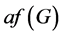 表示。目前,有关反强迫数的结论较少,主要是针对一些图类进行研究。Vukicevic和Trinajstic证明了平行四边形结构六角系统的反强迫数为1 [4] 。随后,六角形链 [5] ,双六角形链 [6] ,一类由四边形和六边形构成的cata型图(cata-condensed Phenylenes) [7] ,富勒烯 [8] ,管状硼氮富勒烯图 [9] 的反强迫数先后得到确定。
表示。目前,有关反强迫数的结论较少,主要是针对一些图类进行研究。Vukicevic和Trinajstic证明了平行四边形结构六角系统的反强迫数为1 [4] 。随后,六角形链 [5] ,双六角形链 [6] ,一类由四边形和六边形构成的cata型图(cata-condensed Phenylenes) [7] ,富勒烯 [8] ,管状硼氮富勒烯图 [9] 的反强迫数先后得到确定。
设 和
和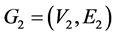 是两个图。两个图
是两个图。两个图 和
和 的卡什积图,记为
的卡什积图,记为 ,是一个以
,是一个以 为顶点集的图,且其中顶点
为顶点集的图,且其中顶点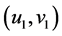 和
和 有边相连当且仅当
有边相连当且仅当 且
且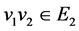 或
或 且
且 。
。
本文主要研究圈和路的卡什积图的反强迫数。我们用 和
和 分别表示顶点数为
分别表示顶点数为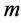 和
和 的圈和路。本文第一部分根据非二部图有唯一完美匹配的必要条件,证明了
的圈和路。本文第一部分根据非二部图有唯一完美匹配的必要条件,证明了 和
和 的反强迫数都为
的反强迫数都为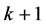 。第二部分根据二部图有唯一完美匹配的必要条件,得到
。第二部分根据二部图有唯一完美匹配的必要条件,得到 的反强迫数为
的反强迫数为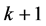 。对
。对
 ,我们证明了其反强迫数恒为3。
,我们证明了其反强迫数恒为3。
2. 奇长圈和路的卡什积图的反强迫数
为了保证有完美匹配,我们只讨论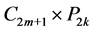 的情形。此部分主要基于以下关于一个图有唯一完美匹配的必要条件。
的情形。此部分主要基于以下关于一个图有唯一完美匹配的必要条件。
引理2.1 [10] 若一个连通图 恰好有一个完美匹配,则
恰好有一个完美匹配,则 有一条割边属于此完美匹配。
有一条割边属于此完美匹配。
定理2.2 
证明 易见,去掉图1中所示的内外两个三角形之间的两条虚线标记的边后,因为内外两个三角形之间必须有奇数条匹配边,所以内外两个三角形之间剩余的边必须是匹配边,这样我们可确定出 的余子图中的唯一完美匹配。于是这两条虚边构成
的余子图中的唯一完美匹配。于是这两条虚边构成 的一个反强迫集,从而
的一个反强迫集,从而 。另外,设
。另外,设 是
是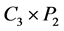 的一个最小的反强迫集,则
的一个最小的反强迫集,则 只有唯一完美匹配。根据引理2.1,
只有唯一完美匹配。根据引理2.1,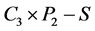 有一条割边,而
有一条割边,而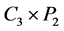 的边割大小至少是3,为产生一条割边,
的边割大小至少是3,为产生一条割边, 至少需要去掉两条边,即
至少需要去掉两条边,即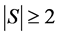 。于是
。于是 得证。■
得证。■
设 为图
为图 的一个完美匹配。一个圈称为
的一个完美匹配。一个圈称为 的
的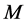 -交替圈是指圈中的边由
-交替圈是指圈中的边由 和非
和非 的边交替组成。因为通过交换交替圈中的匹配边和非匹配边,我们可以得到
的边交替组成。因为通过交换交替圈中的匹配边和非匹配边,我们可以得到 的另一个完美匹配,所以我们有以下结论:
的另一个完美匹配,所以我们有以下结论:

Figure 1. The dashed lines form an anti-forcing set
图1. 虚线所示边构成一个反强迫集
引理2.3 设 为图
为图 的一个边子集。若
的一个边子集。若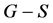 只包含
只包含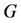 的唯一完美匹配
的唯一完美匹配 ,则
,则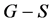 没有
没有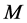 -交替圈。
-交替圈。
为了后面讨论方便,我们先给 的点和边进行标记(见图2),我们称
的点和边进行标记(见图2),我们称 为
为 的第
的第 层(
层( ),记为
),记为 。当
。当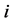 为奇(偶)数时,我们称
为奇(偶)数时,我们称 为
为 的奇(偶)层。我们称属于
的奇(偶)层。我们称属于 某层的边为路边,不属于任一层的边称为圈边。
某层的边为路边,不属于任一层的边称为圈边。
利用数学归纳法,我们可以证明以下结论:
定理2.4 
证明 令 (见图2虚线标记的边),下证
(见图2虚线标记的边),下证 为
为 的一个反强迫集。因为
的一个反强迫集。因为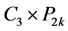 的奇数层之间必须有奇数条匹配边,所以第一层
的奇数层之间必须有奇数条匹配边,所以第一层 中剩余的边
中剩余的边 必须是匹配边。则
必须是匹配边。则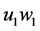 此时也可确定为匹配边。又因为在
此时也可确定为匹配边。又因为在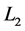 中去掉了
中去掉了 ,所以
,所以 中只有
中只有 可作为匹配边。依次匹配下去,可知
可作为匹配边。依次匹配下去,可知 的唯一完美匹配(见图2)为
的唯一完美匹配(见图2)为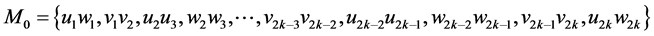 ,由
,由 知
知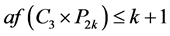 。
。
下面对 用数学归纳法证明
用数学归纳法证明 。
。
当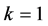 时,由定理2.2知结论成立。假设结论对所有小于
时,由定理2.2知结论成立。假设结论对所有小于 的情形成立,下面对
的情形成立,下面对 进行讨论。设
进行讨论。设 是
是 的一个最小的反强迫集,则
的一个最小的反强迫集,则 只有唯一完美匹配,记为
只有唯一完美匹配,记为 。下面我们分两种情况进行讨论:
。下面我们分两种情况进行讨论:
情形1. 存在某个 ,使得
,使得 ,即偶层
,即偶层 不含匹配边。
不含匹配边。
此时 可分解为两个三长圈和路的卡什积图,分别记为
可分解为两个三长圈和路的卡什积图,分别记为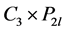 和
和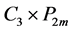 ,其中
,其中 。根据假设,
。根据假设,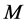 也分解为两部分
也分解为两部分 和
和 ,分别为
,分别为 和
和 的完美匹配。记
的完美匹配。记 ,
,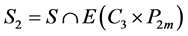 。因为
。因为 是
是 的唯一完美匹配,故
的唯一完美匹配,故 和
和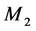 也分别为
也分别为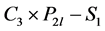 和
和 中的唯一完美匹配。于是
中的唯一完美匹配。于是 和
和 分别为
分别为 和
和 的反强迫集。根据归纳假设,
的反强迫集。根据归纳假设, ,
, 。从而
。从而 。
。
情形2.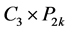 的每个偶层都至少有一条边是匹配边。
的每个偶层都至少有一条边是匹配边。
因为 的每个完美匹配只能包含每个偶层的偶数条边,所以
的每个完美匹配只能包含每个偶层的偶数条边,所以 与每个偶层都交于恰好2条边。
与每个偶层都交于恰好2条边。
不妨假设 ,则
,则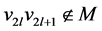 ,故
,故 ,依此类推,我们可确定
,依此类推,我们可确定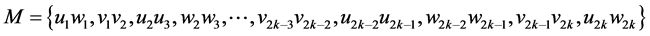 为(见图2)
为(见图2) 的唯一完
的唯一完
美匹配,交每个偶层恰好两条边,每个奇层一条边。
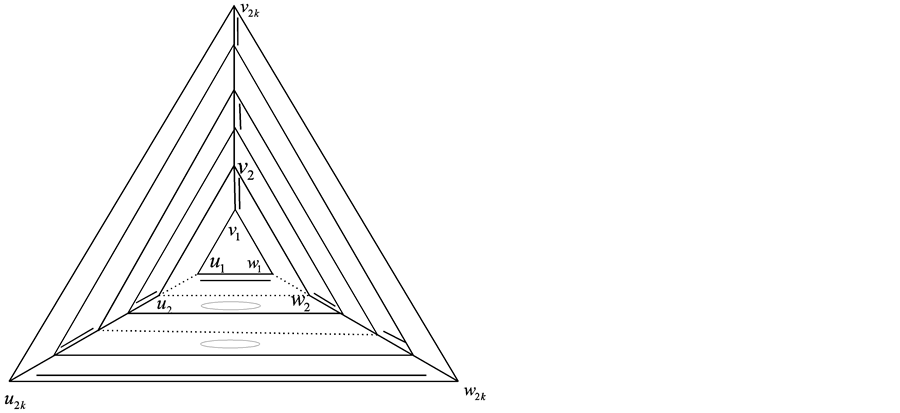
Figure 2. Illustration for the proof of Theorem 2.4
图2. 定理2.4的证明示意图
注意到匹配边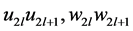 所在的四边形是一个
所在的四边形是一个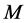 交替圈,根据引理2.3,该四边形的两条圈边
交替圈,根据引理2.3,该四边形的两条圈边 至少有一条属于反强迫集
至少有一条属于反强迫集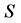 。因为
。因为 共有
共有 个偶层,故
个偶层,故 共有
共有 个这样的
个这样的 交替四边形。每个交替四边形至少有一条圈边属于
交替四边形。每个交替四边形至少有一条圈边属于 。在每个交替四边形各取一条圈边,记这些圈边构成的集合为
。在每个交替四边形各取一条圈边,记这些圈边构成的集合为 ,则
,则 且
且 。进一步,因为
。进一步,因为 只有唯一完美匹配,根据引理2.1,
只有唯一完美匹配,根据引理2.1, 有一条割边。而
有一条割边。而 的最小边割是3,故至少还需要去掉
的最小边割是3,故至少还需要去掉 的两条边才能产生一条割边。于是
的两条边才能产生一条割边。于是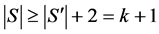 。
。
综上, 。证毕。■
。证毕。■
对于一般奇长圈的卡什积图,我们给出了结论:
定理2.5 
证明 标记 的点和边(见图3(a))。令
的点和边(见图3(a))。令 ,则
,则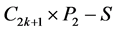 有两条悬挂边(一条边称为一个图的悬挂边是指该边恰有一个端点度数为1)
有两条悬挂边(一条边称为一个图的悬挂边是指该边恰有一个端点度数为1) 可先确定为匹配边,接着可确定
可先确定为匹配边,接着可确定 为匹配边,依次匹配下去,直到点
为匹配边,依次匹配下去,直到点 ,它只能与
,它只能与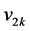 匹配。接着确定匹配边
匹配。接着确定匹配边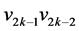 ,依次匹配下去可确定
,依次匹配下去可确定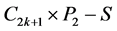 中的唯一完美匹配
中的唯一完美匹配 。则
。则 是一个反强迫集,
是一个反强迫集, 。
。
下证 :设
:设 是
是 的一个最小反强迫集,
的一个最小反强迫集, 是
是 的唯一完美匹配。设
的唯一完美匹配。设 恰有
恰有 条路边为匹配边(
条路边为匹配边( 为奇数)。除这
为奇数)。除这 条边,其余匹配边都是圈边并且包含在
条边,其余匹配边都是圈边并且包含在 个不交的
个不交的 -交替4边形中。根据引理2.3,这些
-交替4边形中。根据引理2.3,这些 -交替4边形至少有一条路边属于
-交替4边形至少有一条路边属于 。在每个交替四边形各取一条路边,记这些路边构成的集合为
。在每个交替四边形各取一条路边,记这些路边构成的集合为 ,则
,则 且
且 。另外,当
。另外,当 时,任两条相邻的匹配路边和它们之间的所有圈边也构成一个
时,任两条相邻的匹配路边和它们之间的所有圈边也构成一个 -交替圈。根据引理2.3,这些
-交替圈。根据引理2.3,这些 -交替圈至少有一条非匹配的圈边属于
-交替圈至少有一条非匹配的圈边属于 (见图3(b)),于是
(见图3(b)),于是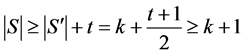 。而当
。而当 时,该匹配路边和
时,该匹配路边和 的所有匹配圈边也确定一个
的所有匹配圈边也确定一个 -交替圈,且该圈不交于
-交替圈,且该圈不交于 (见图3(c))。根据引理2.3,该
(见图3(c))。根据引理2.3,该 -交替圈至少有一条非匹配的边属于
-交替圈至少有一条非匹配的边属于 ,于是
,于是 。■
。■
 (a) (b) (c)
(a) (b) (c)
Figure 3. Illustration for the proof of Theorem 2.5
图3. 定理2.5的证明示意图
3. 偶长圈和路的卡什积图的反强迫数
此部分主要基于以下关于一个二部图有唯一完美匹配的必要条件。
引理3.1 [10] 设 是一个只有唯一完美匹配的二部图,则
是一个只有唯一完美匹配的二部图,则 的点可标记为
的点可标记为 使得每条边
使得每条边 。
。
推论3.2 若一个连通二部图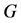 恰好有一个完美匹配,则
恰好有一个完美匹配,则 有两个一度点。
有两个一度点。
证明 设 。因为恰好有一个完美匹配,根据引理3.1,
。因为恰好有一个完美匹配,根据引理3.1,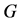 的点可标记为
的点可标记为 ,
,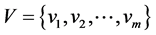 使得每条边
使得每条边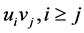 。于是
。于是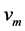 的邻点只有
的邻点只有 ,
, 的邻点只有
的邻点只有 ,即
,即 和
和 为
为 的两个一度点。■
的两个一度点。■
因为 是一个偶长圈,恰有两个完美匹配,故其反强迫集至少包含一条边。另外,去掉其任意一条边,剩余子图只有一个完美匹配,故我们可得以下结论:
是一个偶长圈,恰有两个完美匹配,故其反强迫集至少包含一条边。另外,去掉其任意一条边,剩余子图只有一个完美匹配,故我们可得以下结论:
定理3.3 
定理3.4 
证明 易见,去掉图4中所示的三条虚线标记边后, 的余子图只有唯一完美匹配,于是
的余子图只有唯一完美匹配,于是 。另外,设
。另外,设 是
是 的一个最小的反强迫集,则
的一个最小的反强迫集,则 只有唯一完美匹配,记为
只有唯一完美匹配,记为 。因为
。因为 是二部图,根据推论3.2,
是二部图,根据推论3.2,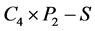 有两个一度点,而
有两个一度点,而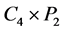 是3-正则图,为产生两个一度点,
是3-正则图,为产生两个一度点, 至少需要去掉三条边,即
至少需要去掉三条边,即 。于是
。于是 得证。■
得证。■
下面我们开始讨论 的反强迫数。为了讨论方便,我们先给
的反强迫数。为了讨论方便,我们先给 的点和边进行标记(见图5),我们称
的点和边进行标记(见图5),我们称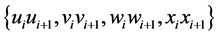 为
为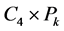 的第
的第 层,记为
层,记为 (
( )。类似地,我们可定义
)。类似地,我们可定义 的奇层,偶层和路边,圈边。
的奇层,偶层和路边,圈边。
定理3.5 
证明 若 为偶数,令
为偶数,令 。则可知
。则可知
 中的悬挂边
中的悬挂边 和
和 为匹配边,依次匹配下去,知
为匹配边,依次匹配下去,知 是唯一完美匹配(见图5(a))。
是唯一完美匹配(见图5(a))。
若 为奇数,则令
为奇数,则令 ,同样可得
,同样可得 是唯一完美匹配(见图5(b))。
是唯一完美匹配(见图5(b))。
不论哪种情况,都有 ,故
,故 。下面对
。下面对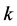 用归纳证明
用归纳证明 (
(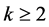 )。
)。
当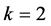 时,由定理3.4知结论成立。假设结论对所有大于2且小于
时,由定理3.4知结论成立。假设结论对所有大于2且小于 的情形都成立,下面对
的情形都成立,下面对 进行讨论。设
进行讨论。设 是
是 的一个最小的反强迫集,则
的一个最小的反强迫集,则 只有唯一完美匹配,记为
只有唯一完美匹配,记为 。下面我们分情况进行讨论:
。下面我们分情况进行讨论:

Figure 4. Illustration for the proof of Theorem 3.4
图4. 定理3.4的证明示意图
 (a) (b)
(a) (b)
Figure 5. Illustration for the proof of Theorem 3.5
图5. 定理3.5的证明示意图
情形1. 存在某个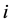 ,使得
,使得 ,即
,即 的第
的第 层的四条边都不在
层的四条边都不在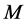 中。
中。
 可分解为两个四长圈和路的卡什积图,分别记为
可分解为两个四长圈和路的卡什积图,分别记为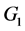 和
和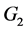 。
。
根据假设, 也可分解为两部分
也可分解为两部分 和
和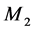 ,分别为
,分别为 和
和 的完美匹配。记
的完美匹配。记 ,
, 。因为
。因为 是
是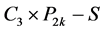 的唯一完美匹配,故
的唯一完美匹配,故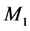 和
和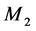 也分别为
也分别为 和
和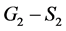 中的唯一完美匹配。这说明
中的唯一完美匹配。这说明 和
和 分别为
分别为 和
和 的反强迫集。
的反强迫集。
当 或
或 时,
时,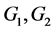 中有一个四边形。不妨设
中有一个四边形。不妨设 为四边形。根据定理3.3,
为四边形。根据定理3.3, 。又
。又 ,根据归纳假设,
,根据归纳假设,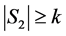 。从而
。从而 。
。
当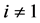 且
且 时,设
时,设 ,
,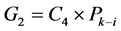 。根据归纳假设,
。根据归纳假设,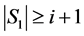 ,
, 。于是
。于是 。
。
情形2. 存在某个 ,使得
,使得 ,即
,即 的第
的第 层的四条边都不在
层的四条边都不在 中。这时与
中。这时与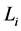 的相邻的层只能有0条匹配边,该情形即为情形1。
的相邻的层只能有0条匹配边,该情形即为情形1。
情形3. 对每个 ,
, ,且
,且 。
。
因为 的每个完美匹配只能与每层交于偶数条边,则
的每个完美匹配只能与每层交于偶数条边,则 与每层都交于恰好2条边。根据这两条匹配边的位置,下面分两种子情形进行讨论:
与每层都交于恰好2条边。根据这两条匹配边的位置,下面分两种子情形进行讨论:
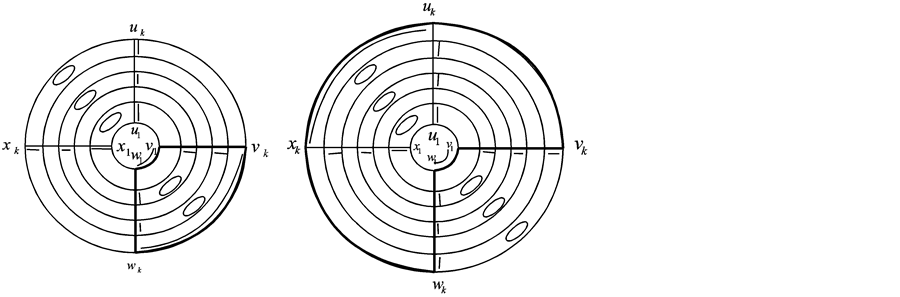
1) 若存在某一层,其两条匹配边位于该层的相对位置(见图6)。
不妨设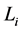 中
中 。因为
。因为 只有两条匹配边,则
只有两条匹配边,则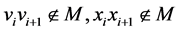 。于是
。于是 。而
。而 只能有两条匹配边
只能有两条匹配边 ,且这两条匹配边也是位于相对位置。类似地,我们可推出
,且这两条匹配边也是位于相对位置。类似地,我们可推出 在每层的2条匹配边都位于相对位置。但进行到第一层时,会产生两个不相邻的点(见图6),其邻点已跟其它点匹配,这与
在每层的2条匹配边都位于相对位置。但进行到第一层时,会产生两个不相邻的点(见图6),其邻点已跟其它点匹配,这与 是完美匹配矛盾。
是完美匹配矛盾。

Figure 6. Illustration for the proof of Case 3(1) of Theorem 3.5
图6. 定理3.5情形3(1)的证明示意图
 (a) (b)
(a) (b)
Figure 7. Illustration for the proof of Case 3(2) of Theorem 3.5
图7. 定理3.5情形3(2)的证明示意图

Figure 8. Illustration for the proof of Theorem 3.6
图8. 定理3.6的证明示意图
2) 与任意一层的两条匹配边都位于相近位置(见图7)。
与任意一层的两条匹配边都位于相近位置(见图7)。
不妨设 中
中 。因为
。因为 只有两条匹配边,则
只有两条匹配边,则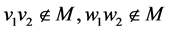 。于是
。于是 是
是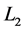 仅有的两条匹配边。依次类推,可知在奇数层
仅有的两条匹配边。依次类推,可知在奇数层 ,我们有
,我们有 。而在偶数层
。而在偶数层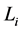 ,我们有
,我们有 。于是当
。于是当 为偶数时,我们可确定
为偶数时,我们可确定 中的唯一完美匹配为
中的唯一完美匹配为  (见图7(a));而当
(见图7(a));而当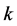 为奇数时,
为奇数时, 中的唯一完美匹配为
中的唯一完美匹配为 (见图7(b))。
(见图7(b))。
注意到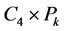 的第1层的两条匹配边
的第1层的两条匹配边 所在的四边形是一个
所在的四边形是一个 交替圈,根据引理2.3,该四边形的两条圈边
交替圈,根据引理2.3,该四边形的两条圈边 至少有一条属于反强迫集
至少有一条属于反强迫集 。
。 的每层都有一个这样的
的每层都有一个这样的 交替四边形,而每个交替四边形至少有一条圈边属于
交替四边形,而每个交替四边形至少有一条圈边属于 ,我们在每个交替四边形各取一条圈边,记这些圈边构成的集合为
,我们在每个交替四边形各取一条圈边,记这些圈边构成的集合为 ,则
,则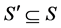 且
且 。
。
当 为偶数时,令
为偶数时,令 (见图7(a))。而当
(见图7(a))。而当 为奇数时,令
为奇数时,令  (见图7(b))。可见
(见图7(b))。可见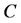 是一个
是一个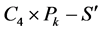 中的
中的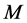 交替圈,根据引理2.3,
交替圈,根据引理2.3, 中至少有一条非匹配边属于
中至少有一条非匹配边属于 。任取
。任取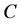 中属于
中属于 的一条非匹配边,记为
的一条非匹配边,记为 。但不论
。但不论 取
取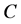 上哪一条非匹配边,都有
上哪一条非匹配边,都有 且
且 中顶点的最小度仍为2。根据推论3.2,
中顶点的最小度仍为2。根据推论3.2, 有两个一度点。因为在
有两个一度点。因为在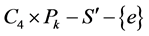 中至少还要去掉一条边才能产生一度点,从而
中至少还要去掉一条边才能产生一度点,从而 除了包含
除了包含 ,还包含另外一条边。于是
,还包含另外一条边。于是 。
。
综上, 。证毕。■
。证毕。■
对于一般的偶圈的卡什积图,我们得到其反强迫数如下:
定理3.6 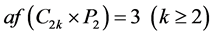
证明 先证 :将
:将 的点和边进行标记(见图8)。令
的点和边进行标记(见图8)。令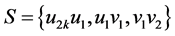 ,则
,则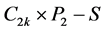 有两条悬挂边
有两条悬挂边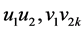 可先确定为匹配边,依次匹配下去,可确定完美匹配
可先确定为匹配边,依次匹配下去,可确定完美匹配 。再证
。再证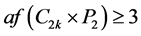 :根据推论3.2,
:根据推论3.2, 去掉一个反强迫集后要有两个一度点。因为
去掉一个反强迫集后要有两个一度点。因为 是3-正则的简单图,所以至少需要去掉3条边才可能产生两个一度点,因此
是3-正则的简单图,所以至少需要去掉3条边才可能产生两个一度点,因此 。综上,
。综上, 。■
。■
基金项目
海南省自然科学基金资助项目(114001),海南省自然科学基金资助项目(2016CXTD004)。
文章引用
张勇军,蔡金转. 关于Cm×Pk的反强迫数
On the Anti-Forcing Number of Cm×Pk[J]. 应用数学进展, 2016, 05(03): 435-442. http://dx.doi.org/10.12677/AAM.2016.53054
参考文献 (References)
- 1. Klein, D. and Randic, M. (1987) Innate Degree of Freedom of a Graph. Journal of Computational Chemistry, 8, 516-521. http://dx.doi.org/10.1002/jcc.540080432
- 2. Randic, M. and Klein, D. (1985) Kekule Valence Structures Revisited. Innate Degrees of Freedom of π-Electron Couplings. In: Trinajstic, N., Ed., Mathematics and Computational Concepts in Chemistry, Hor-wood/Wiley, New York, 274-282.
- 3. Harary, F., Klein, D. and Zivkovic, T. (1991) Graphical Properties of Polyhexes: Perfect Matching Vector and Forcing. Journal of Mathematical Chemistry, 6, 295-306. http://dx.doi.org/10.1007/BF01192587
- 4. Vukicevic, D. and Trinajstic, N. (2007) On the Anti-Forcing Number of Benzenoids. Journal of Mathematical Chemistry, 42, 575-583. http://dx.doi.org/10.1007/s10910-006-9133-6
- 5. Deng, H. (2007) The Anti-Forcing Number of Hexagonal Chains. MATCH Communications in Mathematical and in Computer Chemistry, 58, 675-682.
- 6. Deng, H. (2008) The Anti-Forcing Number of Double Hexagonal Chains. MATCH Communications in Mathematical and in Computer Chemistry, 60, 183-192.
- 7. Zhang, Q., Bian, H. and Vumar, E. (2011) On the Anti-Kekule and Anti-Forcing Number of Cata-Condensed phenylenes. MATCH Communications in Mathematical and in Computer Chemistry, 65, 799-806.
- 8. 杨琴. 富勒烯图的反凯库勒数和反强迫数[D]: [硕士学位论文]. 兰州: 兰州大学, 2010.
- 9. 蒋晓艳, 程晓胜. 硼氮富勒烯图的反强迫数[J]. 湖北师范学院学报(自然科学版), 2013, 33(3): 28-30.
- 10. Lovasz, L. and Plummer, M.D. (1986) Matching Theory. Annals of Discrete Mathematics Vol. 29, North-Holland, Amsterdam.
*通讯作者。