Advances in Applied Mathematics
Vol.04 No.02(2015), Article ID:15351,7
pages
10.12677/AAM.2015.42026
The Researches of the Continuous Axiom of Erceg’s Pseudo-Metric and the Relationships between Its Basic Spheres
Peng Chen, Zhijuan Hu, Xiao Yang, Mengjie Jin, Leilei Liu, Zhigang Tian
Mathematics and Statistics Institute, Henan University of Science and Technology, Luoyang Henan
Email: chenpengbeijing@sina.com
Received: May 7th, 2015; accepted: May 22nd, 2015; published: May 29th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, by comparing the axioms of Erceg-Peng metric and classical metric, we have proved that there is no intrinsic relationship between the topology induced by Erceg metric and the continuous condition in its axioms, and further given some relationships of several types of basic spheres in Erceg-Peng’s pseudo-metric.
Keywords:Induced Topology, Erceg-Peng’s Axiom, Ur Open Mapping, Br Closed Mapping
Erceg伪度量连续性公理及其基本球的关系的研究
陈鹏,胡志娟,杨晓,金梦洁,刘磊磊,田志钢
河南科技大学数学与统计学院,河南 洛阳
Email: chenpengbeijing@sina.com
收稿日期:2015年5月7日;录用日期:2015年5月22日;发布日期:2015年5月29日

摘 要
该文通过对Erceg-Peng公理与经典度量公理进行比较,证明了它的诱导拓扑与Erceg-Peng度量公理的连续性条件没有本质的联系,并且还进一步给出Erceg-Peng的一些基本球之间的一些相互关系。
关键词 :诱导拓扑,Erceg-Peng公理,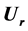 开映射,
开映射,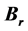 闭映射
闭映射

1. 引言和预备
自从Erceg M.A.在文献[1] 中引入伪度量概念以来,格上度量理论已取得了很大的发展 [1] - [7] 。Erceg M.A.的伪度量定义是基于集合间的Hausdorff距离而引入的 [8] 。
为了研究Erceg度量,本文从另一个角度通过对Erceg-Peng度量公理与一般拓扑学中度量公理进行比较,我们猜测Erceg-Peng度量公理的连续性条件对它的诱导拓扑没有本质的影响,从而,从拓扑学角度出发,Erceg度量公理可以进行简化,为了证明这种猜测,我们先列出一般拓扑学中公理如下:
定义1.1 [9] 设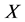 是一个不空集合,一个伪拟度量(简称p.q.度量)是一个映射
是一个不空集合,一个伪拟度量(简称p.q.度量)是一个映射 满足下列条件:
满足下列条件:
(A1) ,如果
,如果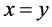 ,那么
,那么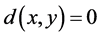 ;
;
(A2) ,
, 。
。
一个p.q.度量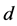 称为伪度量(简称p.度量),如果
称为伪度量(简称p.度量),如果 还满足:
还满足:
(A3) 。
。
除(A1),(A2),(A3)外,如果 还满足:
还满足:
(A4) ,则
,则 ,
,
那么称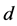 是在
是在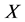 上的一个度量。
上的一个度量。
由于Erceg度量的定义较为复杂且直观意义不明显,鉴于此,1992年,彭育威在文 [5] 中最先给出了Erceg伪度量的点式意义的简化形式定义如下:
定义1.2 [5] 格 上的Erceg-Peng伪拟度量(简称Erceg-Peng p.q.度量)就是满足下列条件的函数
上的Erceg-Peng伪拟度量(简称Erceg-Peng p.q.度量)就是满足下列条件的函数 :
:
(B1)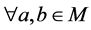 ,如果
,如果 ,那么
,那么 ;
;
(B2) ,
,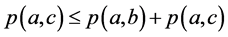 ;
;
(B3) ,
,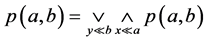 。
。
一个Erceg-Peng伪拟度量 被称为Erceg-Peng伪度量,如果
被称为Erceg-Peng伪度量,如果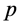 还满足下列条件:
还满足下列条件:
(B4)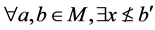 使得
使得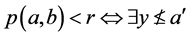 使得
使得 。
。
除(B1),(B2),(B3)和(B5)外,如果 还满足下列条件:
还满足下列条件:
(B5)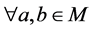 ,如果
,如果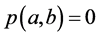 则
则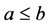 ,
,
那么称 是在
是在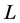 上的一个Erceg-Peng度量。
上的一个Erceg-Peng度量。
在Erceg-Peng度量公理中,如去掉(B3),显然定义1.1就是定义1.2的特殊形式。其中(B1),(B2),(B5)分别是(A1),(A2)和(A4)的推广,(B1),(B5)分别与(A1),(A4)的差异是由于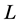 上带有序的结构;(B4)体现了
上带有序的结构;(B4)体现了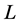 完全分配格的对合对应的性质,它是(A3)的推广。
完全分配格的对合对应的性质,它是(A3)的推广。
通过比较,发现在定义1.1中没有条件与(B3)对应,由此我们猜测:在Erceg-Peng度量公理中的条件(B3)对它所诱导的拓扑没有实质的作用,即去掉(B3),这将不会改变它所诱导的基本拓扑性质。为了证明这种猜测的正确,现给出一些必要的定义和引理。
定义1.3设 是一个映射。且对
是一个映射。且对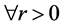 ,定义映射
,定义映射 为:
为: 。另外还分别定义映射
。另外还分别定义映射 和
和 使得
使得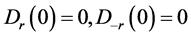 且当
且当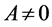 时,
时,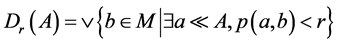 和
和 。
。
引理1.4 设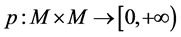 是映射,则
是映射,则 。
。
证明:如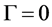 ,则结论显然。不妨设
,则结论显然。不妨设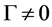 。根据
。根据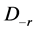 的定义知
的定义知 。因此
。因此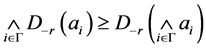 。反过来,设
。反过来,设 ,则
,则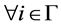 有
有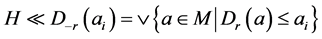 ,从而
,从而 使得
使得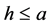 且
且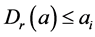 。根据
。根据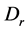 的定义可得
的定义可得 ,所以
,所以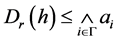 。由此得
。由此得 ,由
,由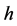 的任意性知
的任意性知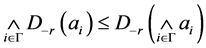 。综述命题得证。
。综述命题得证。
引理1.5 如果映射 满足(B4),则
满足(B4),则 。
。
证明:设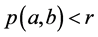 。对每个
。对每个 (也就是
(也就是 ),
),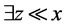 且
且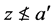 (也就是
(也就是 且
且 ,根据(B4),
,根据(B4),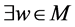 且
且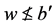 使得
使得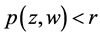 。由此有
。由此有 ,(否则,存在
,(否则,存在 使
使 并且
并且 ,但从
,但从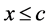 和
和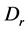 定义,有
定义,有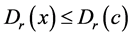 ,因此
,因此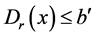 ,再根据
,再根据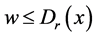 得
得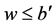 ,矛盾)。这表明只要
,矛盾)。这表明只要 就有
就有 ,因此
,因此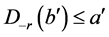 ,即
,即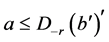 。所以
。所以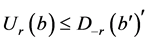 。
。
反过来,设 且
且 ,则
,则 ,即
,即 使得
使得 。根据(B4),知
。根据(B4),知 使得
使得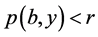 。所以
。所以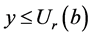 。由
。由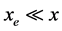 和
和 得
得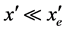 和
和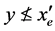 ,因此有
,因此有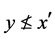 。根据
。根据 与
与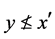 得
得 ,即
,即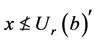 。这就是说只要
。这就是说只要 就有
就有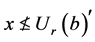 ,因而可得
,因而可得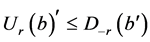 ,即
,即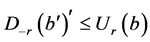 。综上所述,命题得证。
。综上所述,命题得证。
引理1.6 如果映射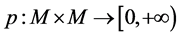 满足(B4),则
满足(B4),则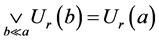 。
。
证明 由引理1.4,引理1.5和DeMorgan对合律可得下面等式:

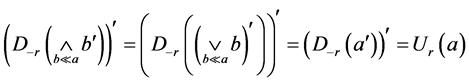
引理1.7 设 是一个满足(B1),(B2)和(B4)的映射,则为
是一个满足(B1),(B2)和(B4)的映射,则为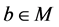 ,
,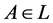 及
及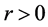 ,有下列结论:
,有下列结论:
1) ;
;
2)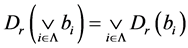 ;
;
3)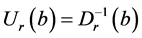 ;
;
4)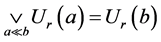 ;
;
5)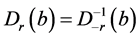 。
。
证明 1)和2)是显然的。
3) 由 。再根据引理1.5显然。
。再根据引理1.5显然。
4) 由引理1.6得。
5) 从3)和4)有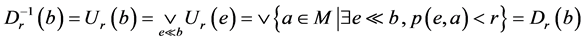 ,因而(5)获得证明。
,因而(5)获得证明。
定义1.8 设 是一个满足(B1),(B2)和(B4)的映射,对每个
是一个满足(B1),(B2)和(B4)的映射,对每个 和
和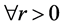 ,定义一个映射
,定义一个映射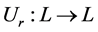 使得
使得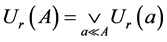 。
。
注1.9 首先,在这定义中,如果 ,那么
,那么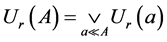 演变为
演变为 ,这与前面引理1.6结论相一致,这说明如此定义
,这与前面引理1.6结论相一致,这说明如此定义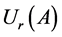 是有意义且与定理1.6不矛盾。其次,根据引理1.6和定义1.3,对每个
是有意义且与定理1.6不矛盾。其次,根据引理1.6和定义1.3,对每个 和
和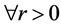 ,可得
,可得 。因此在本文后面的论述和证明中,对它们两者不加区别,等同看待。
。因此在本文后面的论述和证明中,对它们两者不加区别,等同看待。
在本文我们规定: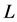 表示一个具有逆序对合对应“
表示一个具有逆序对合对应“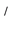 ”的完全分配格,简称fuzzy格;
”的完全分配格,简称fuzzy格;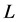 中所有非
中所有非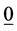 的
的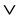 -既约元(也被称为点)的集合记为
-既约元(也被称为点)的集合记为 (或
(或 );
); 中每个元
中每个元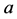 都有一个最大极小集用
都有一个最大极小集用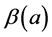 表示,且易见
表示,且易见
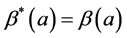 也是
也是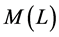
 的一个极小集,
的一个极小集,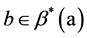 当且仅当
当且仅当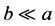 ,这里
,这里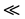 恰是
恰是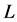 上的way below关系 [4] [10] ;定义域是
上的way below关系 [4] [10] ;定义域是 值域是
值域是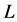 的映射
的映射 定义为
定义为 。
。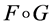 指
指 有
有 ,另外,规定
,另外,规定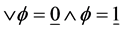 。其它未声明的概念与符号请参考文献 [10] 。
。其它未声明的概念与符号请参考文献 [10] 。
2. Fuzzy p-度量及与Erceg’s伪度量的关系
定理2.1 如果 是一个满足(B1),(B2)和(B4)的映射(称p是L上的一个Fuzzy p-度量),则有下列结论:
是一个满足(B1),(B2)和(B4)的映射(称p是L上的一个Fuzzy p-度量),则有下列结论:
(D1)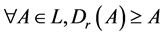 ;
;
(D2)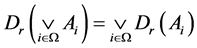 ;
;
(D3)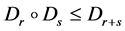 ;
;
(D4) ;
;
(D5) 。
。
证明. 根据引理1.7,命题显然成立。
定理2.2 如果p是一个满足(B1),(B2)和(B4)的映射,那么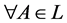 ,有如下结论:
,有如下结论:
1)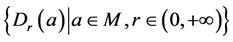 是一个在
是一个在 上的拓扑基,记这个拓扑为
上的拓扑基,记这个拓扑为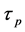 。
。
2) 。
。
3)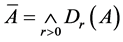 。
。
证明. 根据定理2.1和文[4] 中的主要结论得命题成立。
推论2.3 设p是满足(B1),(B2)和(B4)的映射,则:
1)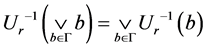 ;
;
2)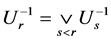 ;
;
3)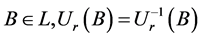 。
。
因此,如果 是一个满足(B1),(B2)和(B4)的映射,则根据定理2.1和定理2.2知:由这组(D1)~(D5)条件按定义
是一个满足(B1),(B2)和(B4)的映射,则根据定理2.1和定理2.2知:由这组(D1)~(D5)条件按定义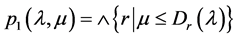 获得一个Erceg伪度量
获得一个Erceg伪度量 并且
并且 ,这里
,这里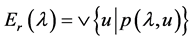 。梁基华曾经在文 [4] 中给出的与之满足(D1)~(D5)映射相对应的那个Erceg伪度量
。梁基华曾经在文 [4] 中给出的与之满足(D1)~(D5)映射相对应的那个Erceg伪度量 只不过是满足这组给定的(D1)~(D5)的所有映射组成的代表类其中的一个特定代表而已。
只不过是满足这组给定的(D1)~(D5)的所有映射组成的代表类其中的一个特定代表而已。
3. Erceg伪度量函数的简化
本节在Erceg-Peng伪度量基础上对它的度量函数做进一步的简化。
定理3.1 一个映射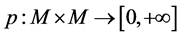 是
是 上的Erceg伪度量当且仅当
上的Erceg伪度量当且仅当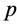 满足条件(B1),(B2),(B4)和下面(B3)*。
满足条件(B1),(B2),(B4)和下面(B3)*。
(B3)* 
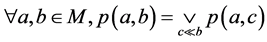
证明 设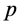 是Erceg伪度量,则
是Erceg伪度量,则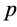 满足(B1),(B2)和(B4),下证
满足(B1),(B2)和(B4),下证 满足(B3)*由于
满足(B3)*由于 ,
,
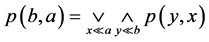
因此 ,有
,有 。由此利用
。由此利用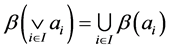 得
得

从而 。因此
。因此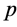 满足(B3)*。
满足(B3)*。
反之,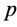 满足(B1),(B2),(B3)*和(B4)下证
满足(B1),(B2),(B3)*和(B4)下证 满足(B3)。
满足(B3)。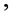
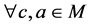 如果
如果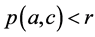 ,则有
,则有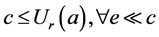 ,由引理1.6和极小集的保并知
,由引理1.6和极小集的保并知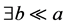 使得
使得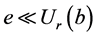 。于是
。于是 。因此有
。因此有 。由
。由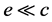 的任意性有
的任意性有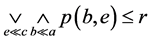 。也就是如
。也就是如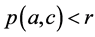 就有
就有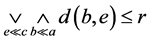 ,因此
,因此
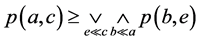 .
.
其次, ,由(B1)和(B2)得
,由(B1)和(B2)得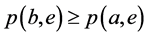 。于是
。于是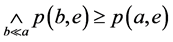 ,因
,因 满足(B3),所以
满足(B3),所以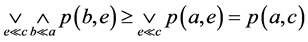 ,因此
,因此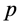 是Erceg伪度量。证毕。
是Erceg伪度量。证毕。
定义3.2 设 是一个从
是一个从 的映射。
的映射。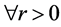 ,定义映射
,定义映射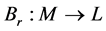 如下:
如下: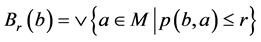 ,称
,称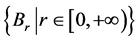 为
为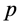 的闭邻域映射簇(简称C-nbd簇)。
的闭邻域映射簇(简称C-nbd簇)。
定理3.3 设映射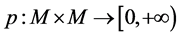 满足(B1)和(B2)。则
满足(B1)和(B2)。则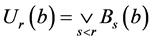 。
。
证明 假设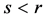 ,那么
,那么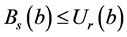 。因此
。因此 。反过来,
。反过来, ,有
,有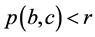 。取
。取 使得
使得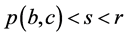 。于是
。于是 ,从
,从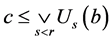 。因此
。因此 。
。
定理3.4 设 是
是 上的Erceg伪拟度量,
上的Erceg伪拟度量,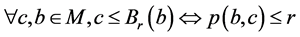 。
。
证明 只须证明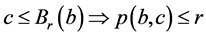 。取
。取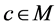 且
且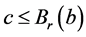 。那么
。那么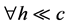 ,
,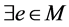 使得
使得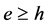 且
且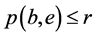 。由
。由 满足(B1)和(B2)可知
满足(B1)和(B2)可知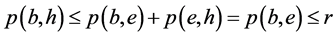 。因此由(B3)*得
。因此由(B3)*得 。
。
注意:由于我们对Erceg度量进行了简化,因此一个映射 如果满足(B1),(B2)和(B3)*,(B4)和(B5),则我们也习惯地称
如果满足(B1),(B2)和(B3)*,(B4)和(B5),则我们也习惯地称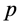 是Erceg伪拟度量(Erceg度量)。这和前面Erceg伪拟度量定义有一点差别。因为(B3)*代替(B3)的简化是借助于(B4),但这里如此称呼是与(B4)无关,不过它们的区别是显然的,在论述和证明中体现,一目了然,因而这不影响后面涉及的有关论述和证明。
是Erceg伪拟度量(Erceg度量)。这和前面Erceg伪拟度量定义有一点差别。因为(B3)*代替(B3)的简化是借助于(B4),但这里如此称呼是与(B4)无关,不过它们的区别是显然的,在论述和证明中体现,一目了然,因而这不影响后面涉及的有关论述和证明。
定理3.5 设 是
是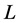 上的Erceg伪度量,则它的闭邻域映射簇
上的Erceg伪度量,则它的闭邻域映射簇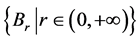 满足下面条件:
满足下面条件:
(R1)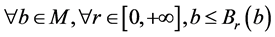 ;
;
(R2)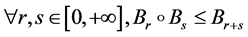 ;
;
(R3)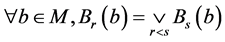 ;
;
(R4) 。
。
证明 (R1) 这能够被获得从定理3.4和(B1)。
(R2) 根据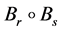 的定义,这能够被获得从定理3.4和(B2)。
的定义,这能够被获得从定理3.4和(B2)。
(R3) 由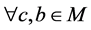 ,
,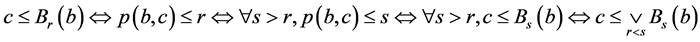 。可证。
。可证。
(R4) 根据(B4)和定理3.3易得(B4)。
定理3.6 设映射簇 满足(R1)-(R4),定义映射
满足(R1)-(R4),定义映射 如下:
如下:
 ,
,
则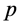 是
是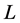 上的一个Erceg伪度量,且
上的一个Erceg伪度量,且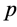 的闭邻域映射簇恰是
的闭邻域映射簇恰是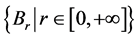 。
。
证明 首先证明下列结果: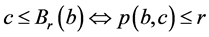 (1)。
(1)。
根据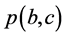 定义和(R3),
定义和(R3),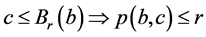 是显然的。反过来,让
是显然的。反过来,让 .
.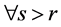 ,根据
,根据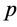 的定义有
的定义有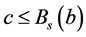 。由(R3)知
。由(R3)知 。
。
(B1) 能够从(R1)获得。
(B2) 假设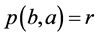 和
和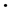
 那么
那么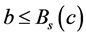 和
和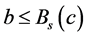 。因此
。因此 。从(R2)知道
。从(R2)知道 ,由此
,由此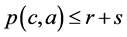 . 即
. 即 。
。
(B3) 由: 可得。
可得。
(B4) 从(R2)和定理3.3可得。
最后, 的闭邻域映射簇恰好是
的闭邻域映射簇恰好是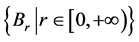 ,这可由定理3.4和(1)得。证毕。
,这可由定理3.4和(1)得。证毕。
在一个Erceg伪度量里,由引理1.7知有 和
和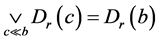 成立。受此启发,我们断言在Erceg伪度量里,其它基本球也有相似性质。现给出下列几个结果。
成立。受此启发,我们断言在Erceg伪度量里,其它基本球也有相似性质。现给出下列几个结果。
定理3.7 设p是Erceg伪度量,则 。
。
证明 因为 ,由
,由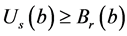 ,得
,得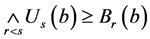 ,另外根据定理3.5中(R3)可得
,另外根据定理3.5中(R3)可得 ,从而命题成立。
,从而命题成立。
定理3.8 如果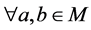 ,p是一个Erceg伪度量
,p是一个Erceg伪度量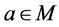 且
且 令
令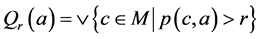 ,那么
,那么
1)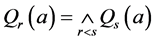 ;
;
2)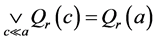 。
。
证明 1)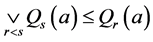 显然。另一方面,取
显然。另一方面,取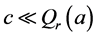 则
则 使得
使得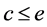 和
和 。根据(B1)和(B2)有
。根据(B1)和(B2)有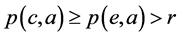 。取
。取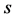 使得
使得 .那么有
.那么有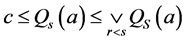 。这显示
。这显示 。
。
2) 显然 ,让
,让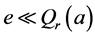 。从(B1)和(B2),可得到
。从(B1)和(B2),可得到 。如果
。如果 ,那么有
,那么有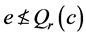 为每个
为每个 ,这暗示
,这暗示 。因此
。因此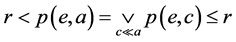 。这是一个矛盾。因此,
。这是一个矛盾。因此,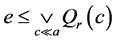 。从而
。从而 。
。
定理3.9 如果 是一个Erceg伪度量,那么
是一个Erceg伪度量,那么
1)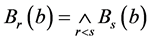 ;
;
2)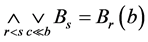 。
。
证明 1) 显然。反过来,假设
显然。反过来,假设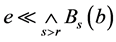 ,那么对每个
,那么对每个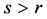 ,我们有
,我们有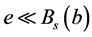 。从(B1)和(B2) 可得
。从(B1)和(B2) 可得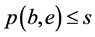 ,所以
,所以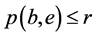 。从而
。从而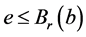 。由此
。由此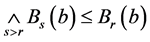 。
。
2) 如果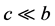 ,那么
,那么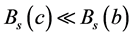 对每个
对每个 。因此
。因此 。从(1),我们有
。从(1),我们有 。又因为
。又因为 。从引理1.7和定理3.7,我们可知
。从引理1.7和定理3.7,我们可知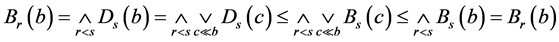 。
。
定理3.10 如果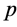 是一个Erceg伪度量,那么
是一个Erceg伪度量,那么
1) ;
;
2) 。
。
证明 1)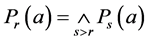 显然。反过来,让
显然。反过来,让 ,那么对每个
,那么对每个 ,我们有
,我们有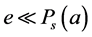 ,那蕴含
,那蕴含 ,由此
,由此 。因此
。因此 。从而
。从而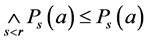 。
。
2) 显然 。其次,如果
。其次,如果 ,那么
,那么 。因此我们有
。因此我们有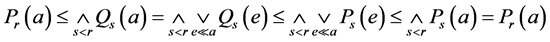 。
。
定理3.11 设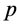 是Erceg伪度量,则
是Erceg伪度量,则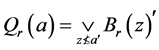 。
。
证明 假设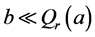 。根据定理3.8知
。根据定理3.8知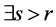 使得
使得 。由此得
。由此得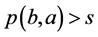 。假如
。假如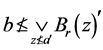 ,那么对每个
,那么对每个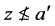 有
有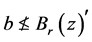 ,也就是,
,也就是,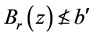 。因此,存在
。因此,存在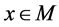 使得
使得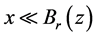 且
且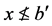 。因此
。因此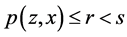 。根据(B2),存在
。根据(B2),存在 使得
使得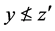 且
且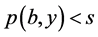 。让
。让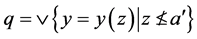 。那么
。那么 ,即
,即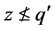 。因为
。因为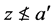 蕴含
蕴含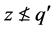 。所以得
。所以得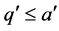 ,也就是
,也就是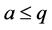 。因此
。因此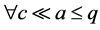 ,存在
,存在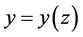 使
使 。
。 。又根据(B3)*得
。又根据(B3)*得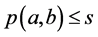 。这矛盾
。这矛盾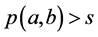 ,这显示
,这显示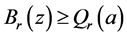 。另一方面,假设
。另一方面,假设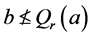 。那么
。那么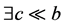 使得
使得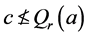 。所以对每个
。所以对每个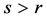 有
有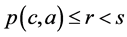 。对每个
。对每个 (也就是
(也就是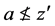 ),根据(B4)存在
),根据(B4)存在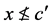 ,使得
,使得 。因此有
。因此有 。再由于
。再由于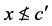 ,所以有
,所以有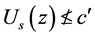 (即
(即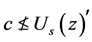 )。这可推
)。这可推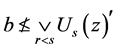 。根据定理3.7可得
。根据定理3.7可得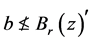 。由
。由 获得
获得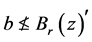 。因此
。因此 。所以,
。所以,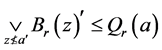 。
。
定理3.12 假设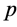 是Erceg伪度量。那么
是Erceg伪度量。那么 。
。
证明 首先,证明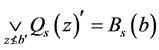 。假设
。假设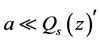 。那么由极小集性质知
。那么由极小集性质知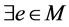 使得
使得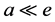 且
且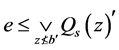 ,也就是
,也就是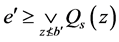 。这显示对每点
。这显示对每点 ,存在
,存在 使得
使得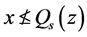 ,由此可推出
,由此可推出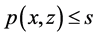 。取
。取 。从(B4)可知存在
。从(B4)可知存在 使得
使得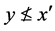 且
且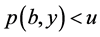 。让
。让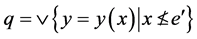 ,那么
,那么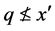 ,也就是
,也就是 。这显示只要
。这显示只要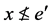 就有
就有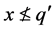 ,因此得
,因此得 (也就是,
(也就是,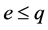 )。根据
)。根据 ,知存在
,知存在 使得
使得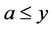 且
且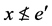 。根据(B1)和(B2),得到
。根据(B1)和(B2),得到 。因
。因 是任意的,所以
是任意的,所以 ,由此有
,由此有 。这显示
。这显示 。
。
其次,证明 ,也就是,
,也就是, 。假设
。假设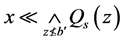 。那么对每个
。那么对每个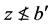 且
且 ,知
,知 使得
使得 且
且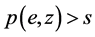 ,由此
,由此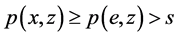 。现证明
。现证明 。假如
。假如 。那么
。那么 。取
。取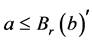 且使得
且使得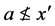 ,则可知
,则可知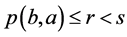 。根据(B4)知存在
。根据(B4)知存在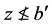 使得
使得 ,这矛盾
,这矛盾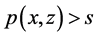 。因此
。因此 。由此
。由此 ,再根据
,再根据 及(R3)有
及(R3)有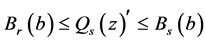 ,命题得证。
,命题得证。
文章引用
陈 鹏,胡志娟,杨 晓,金梦洁,刘磊磊,田志钢, (2015) Erceg伪度量连续性公理及其基本球的关系的研究
The Researches of the Continuous Axiom of Erceg’s Pseudo-Metric and the Relationships between Its Basic Spheres. 应用数学进展,02,209-216. doi: 10.12677/AAM.2015.42026
参考文献 (References)
- 1. Erceg, M.A. (1979) Metric spaces in fuzzy set theory. Journal of Mathematical Analysis and Applications, 69, 205- 230.
- 2. 陈鹏, 史福贵 (2007) Erceg-度量的进一步简化及其性质. 数学进展, 5, 579-586.
- 3. Chen, P. (2011) The relation between two kinds of metrics on lattices. Annals of Fuzzy Sets, Fuzzy Logic and Fuzzy Systems, 1, 175-181.
- 4. 梁基华 (1984) 关于不分明度量空间的几个问题. 数学年刊, 1, 59-67.
- 5. Peng, Y.W. (1993) Simplification of Erceg’s fuzzy metric function and its application. Fuzzy Sets and Systems, 54, 181-189.
- 6. 彭育威 (1996) 对格上Erceg式p.q.(p.)度量的注记. 数学研究与评论, 1, 135-138.
- 7. Shi, F.G. (2001) Pointwise pseu-do-metrics in L-fuzzy set theory. Fuzzy Sets and Systems, 121, 200-216.
- 8. Hausdorff, F. (1957) Set Theory. 2nd Edition, Chelsea, New York.
- 9. Kelley, J.L. (1955) General topology. Stone, M.A., Nirenberg, L. and Chern, S.S., Eds., Van Nostrand, New York.
- 10. 王国俊 (1982) 邻域方法在Fuzzy拓扑学中的困难. 模糊数学, 1, 113-116.