Pure Mathematics
Vol.06 No.03(2016), Article ID:17663,11
pages
10.12677/PM.2016.63036
The Analyticity Properties of a Class of Holomorphic Matrix Functions
Chao Fu, Ningfang Song
School of Science, Beijing University of Posts and Telecommunications, Beijing

Received: May 7th, 2016; accepted: May 23rd, 2016; published: May 26th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we prove an analogue Picard’s little theorem for a special class of holomorphic matrix functions in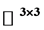 , and also study the relation between asymptotic values and Picard omitting value for holomorphic matrix functions. Moreover, we discuss the properties of complex dynamic system in
, and also study the relation between asymptotic values and Picard omitting value for holomorphic matrix functions. Moreover, we discuss the properties of complex dynamic system in .
.
Keywords:Picard’s Little Theorem, Holomorphic Matrix Functions, Asymptotic Values, Complex Dynamic System

一类全纯矩阵函数的解析性质
付超,宋宁芳
北京邮电大学理学院,北京

收稿日期:2016年5月7日;录用日期:2016年5月23日;发布日期:2016年5月26日

摘 要
本文把Picard定理推广到了一类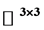 的全纯矩阵函数中,同时探讨了渐近值与Picard例外值之间的关系,最后在
的全纯矩阵函数中,同时探讨了渐近值与Picard例外值之间的关系,最后在 中讨论了一些复动力系统的性质。
中讨论了一些复动力系统的性质。
关键词 :Picard定理,全纯矩阵函数,渐近值,复动力系统

1. 引言和主要结果
整函数是在整个复平面 上全纯的函数。众所周知,整函数的皮卡定理是全纯函数的一个重要性质,它告诉我们:整函数
上全纯的函数。众所周知,整函数的皮卡定理是全纯函数的一个重要性质,它告诉我们:整函数 在
在 中取到每个有穷复值,最多只有一个例外 [1] 。全纯函数的例外值、临界值、完全歧义值、渐近值等的性态一直是复变函数领域中引起人们兴趣的研究内容,在这些方面也有许多丰富的结果 [2] - [4] 。对高维的全纯函数考虑类似的问题是很有意义的,也是很复杂的 [5] [6] 。
中取到每个有穷复值,最多只有一个例外 [1] 。全纯函数的例外值、临界值、完全歧义值、渐近值等的性态一直是复变函数领域中引起人们兴趣的研究内容,在这些方面也有许多丰富的结果 [2] - [4] 。对高维的全纯函数考虑类似的问题是很有意义的,也是很复杂的 [5] [6] 。
本文中我们将整函数的Picard定理推广到一类全纯矩阵函数上,并考虑其例外值的相关性质。为后面叙述方便,下面先介绍一些所需的概念和符号 [2] - [7] :
 表示所有的3阶复矩阵构成的集合;
表示所有的3阶复矩阵构成的集合;
设 ,若在
,若在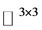 中矩阵
中矩阵 与一个对角矩阵相似,则称
与一个对角矩阵相似,则称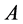 是可对角化矩阵,否则称
是可对角化矩阵,否则称 为不可对角化矩阵,矩阵
为不可对角化矩阵,矩阵 的相似类指的是所有与
的相似类指的是所有与 相似的矩阵构成的集合;
相似的矩阵构成的集合;
 为
为 的子集,
的子集, 表示
表示 的9维复勒贝格测度;
的9维复勒贝格测度;
设 为整函数,
为整函数, 表示
表示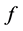 在
在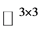 上的自由延拓;
上的自由延拓;
若 ,则称
,则称 为
为 的例外值,记为
的例外值,记为 ,且记
,且记 ;
;
若存在 ,使得
,使得 并且
并且 ,则称点
,则称点 为
为 在
在 上的临界值;
上的临界值;
若 的每一个原像至少是2重的,则称
的每一个原像至少是2重的,则称 为
为 在
在 上的完全歧义值;
上的完全歧义值;
若存在一条趋于无穷的曲线 ,使得
,使得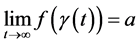 成立,则称
成立,则称 是
是 的渐近值;
的渐近值;
若存在一条趋于无穷的曲线 ,使得
,使得 成立,则称
成立,则称 是
是 的渐近值;
的渐近值;
运用复分析的知识和矩阵分析的技巧,我们研究了 上全纯矩阵函数的解析性质,得到下面的结果。
上全纯矩阵函数的解析性质,得到下面的结果。
定理1:设 是
是 上的非线性整函数,且
上的非线性整函数,且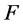 是
是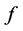 在
在 上的自由延拓,则
上的自由延拓,则 。
。
定理2:设 是
是 上的非线性整函数,且
上的非线性整函数,且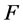 是
是 在
在 上的自由延拓,如果
上的自由延拓,如果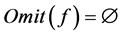 并且
并且
 ,则
,则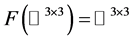 。
。
定理3:设 是
是 上的非线性整函数,且
上的非线性整函数,且 是
是 在
在 上的自由延拓,如果
上的自由延拓,如果 并且
并且
 不存在完全歧义值,则
不存在完全歧义值,则 。
。
更进一步,我们发现上述定理中的条件亦是 成立的必要条件。
成立的必要条件。
定理4:设 是
是 上的非线性整函数,且
上的非线性整函数,且 是
是 在
在 上的自由延拓,如果
上的自由延拓,如果 ,则
,则 ,
, 或
或 不存在完全歧义值。
不存在完全歧义值。
渐近值理论是复分析中重要的理论,我们知道整函数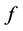 的Picard例外值是渐近值。考虑自由延拓
的Picard例外值是渐近值。考虑自由延拓 的渐近性,我们有类似的结论。
的渐近性,我们有类似的结论。
定理5:设 是
是 上的非线性整函数,且
上的非线性整函数,且 是
是 在
在 上的自由延拓,如果
上的自由延拓,如果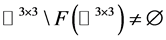 ,则
,则 在
在 中的每一个例外值都是一个渐近值。
中的每一个例外值都是一个渐近值。
另一方面,我们进一步讨论了 上自由延拓的整函数$F$的动力学性质。令
上自由延拓的整函数$F$的动力学性质。令
 ,
,
及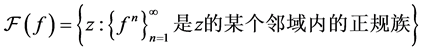 ,
,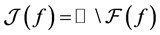 ,
, 称为Fatou集,
称为Fatou集, 称为Julia集。
称为Julia集。
Misiurewicz [8] 证明了 的Julia集为复平面
的Julia集为复平面 。我们受Misiurewicz的启发得到了下面两个结论。
。我们受Misiurewicz的启发得到了下面两个结论。
定理6:设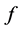 是
是 上的非线性整函数,且
上的非线性整函数,且 是
是 在
在 上的自由延拓,如果
上的自由延拓,如果 ,则
,则
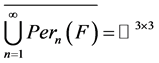 。
。
定理7:设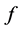 是
是 上的非线性整函数,且
上的非线性整函数,且 是
是 在
在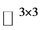 上的自由延拓,如果
上的自由延拓,如果 ,则
,则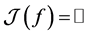 。
。
2. 引理
为了证明定理,我们需要下面的引理。
引理1:如果 ,则
,则 。
。
证明:因为集合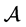 在
在 中是有限个低维复子流形的并集,并且每一个复子流形最多是在8维的复空间中,所以我们可以得到
中是有限个低维复子流形的并集,并且每一个复子流形最多是在8维的复空间中,所以我们可以得到 。
。
引理2:如果 是
是 中所有可对角化矩阵构成的集合,则
中所有可对角化矩阵构成的集合,则 ,其中
,其中 是所有3阶非奇异复矩阵构成的集合。
是所有3阶非奇异复矩阵构成的集合。
证明:设 是
是 中所有不可对角化矩阵构成的集合,表示集合中的每一个矩阵至少有两个相同的特征值,我们可以得到
中所有不可对角化矩阵构成的集合,表示集合中的每一个矩阵至少有两个相同的特征值,我们可以得到 。因为
。因为 在
在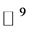 中是有限个低维复子流形的并集,并且每一个复子流形最多是在8维的复空间中。从而可以得到
中是有限个低维复子流形的并集,并且每一个复子流形最多是在8维的复空间中。从而可以得到 ,故
,故 。
。
下面引理3是关于矩阵谱的连续性结果。
引理3: [9] :设 ,
, 为
为 的谱集,
的谱集, 为
为 的谱集,两个谱集之间的距离定义为
的谱集,两个谱集之间的距离定义为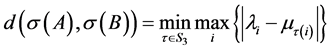 ,其中
,其中 是3元置换群,则
是3元置换群,则 上的距离函数
上的距离函数 是连续的。
是连续的。
除此之外,我们还需要复动力系统中的几个重要结论。
引理4: [10] [11] : 设 为整函数,则
为整函数,则 为斥性周期点的闭包。
为斥性周期点的闭包。
引理5: [10] [11] : 设 为整函数,则
为整函数,则 的任一连通分支为以下类型之一:吸引周期分支、超吸引周期分支、抛物周期分支、Siegel盘、Baker分支、预周期分支、游荡分支。
的任一连通分支为以下类型之一:吸引周期分支、超吸引周期分支、抛物周期分支、Siegel盘、Baker分支、预周期分支、游荡分支。
3. 定理1的证明
证明:设 ,且
,且 可以对角化,则存在非奇异矩阵
可以对角化,则存在非奇异矩阵 及
及 ,其中
,其中 ,使得
,使得
 。
。
如果 的每一个像都有原像,则对于
的每一个像都有原像,则对于 中的
中的 ,我们有
,我们有 ,其中
,其中 。从而对于
。从而对于 中的所有可对角化矩阵
中的所有可对角化矩阵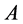 ,存在矩阵
,存在矩阵
 ,
,
使得 成立。
成立。
如果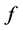 中有一个像没有原像,不妨设
中有一个像没有原像,不妨设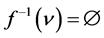 ,
, ,则对于
,则对于 中的一类可对角化矩阵
中的一类可对角化矩阵

不存在 使得
使得 。
。
因为 在所有可对角化矩阵构成的集合中是零测的,所以
在所有可对角化矩阵构成的集合中是零测的,所以 在所有可对角化矩阵构成的集合中稠密。由引理1和引理2可得所有可对角化矩阵构成的集合在
在所有可对角化矩阵构成的集合中稠密。由引理1和引理2可得所有可对角化矩阵构成的集合在 稠密,则
稠密,则 在
在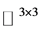 中稠密,所以
中稠密,所以 。
。
4. 定理2和定理3的证明
定理2的证明 (1) 如果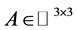 是可以对角化的矩阵, 则存在非奇异矩阵
是可以对角化的矩阵, 则存在非奇异矩阵 及
及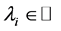 ,其中
,其中 ,使得
,使得
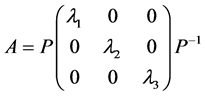 。
。
由于 ,所以存在
,所以存在 ,
,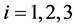 ,使得
,使得 。令
。令
 ,
,
把 代入
代入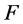 中可得
中可得
 。
。
(2) 否则,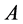 与一个Jordan标准型相似, 即存在非奇异矩阵
与一个Jordan标准型相似, 即存在非奇异矩阵 及
及 ,使得
,使得
 (1)
(1)
或
 (2)
(2)
对于(1)式,因为 ,所以存在
,所以存在 使得
使得 。由
。由 ,可得
,可得 。现在考虑矩阵
。现在考虑矩阵
 ,
,
它的线性无关的特征向量只有一个即 ,所以上述矩阵不可对角化,从而存在非奇异矩阵
,所以上述矩阵不可对角化,从而存在非奇异矩阵 使得
使得
 。
。
令

可得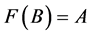 。
。
对于(2)式,因为 ,所以存在
,所以存在 使得
使得 ,
, 又由
又由 可知
可知 。由于矩阵
。由于矩阵

它的线性无关的特征向量只有两个即 ,
, ,所以上述矩阵不可对角化。从而存在非奇异矩阵
,所以上述矩阵不可对角化。从而存在非奇异矩阵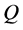 使得
使得
 。
。
令
 ,
,
可得 。
。
定理3的证明 (1) 对于 中可对角化矩阵的证明与定理2的证明相同。
中可对角化矩阵的证明与定理2的证明相同。
(2) 否则,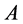 与一个Jordan标准型相似,即存在非奇异矩阵
与一个Jordan标准型相似,即存在非奇异矩阵 及
及 ,使得(1)或(2)成立。对于(1)式,因为
,使得(1)或(2)成立。对于(1)式,因为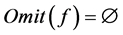 ,所以
,所以 的原像为
的原像为 ,
, ,又因为
,又因为 不存在完全歧义值,所以存在
不存在完全歧义值,所以存在 使得
使得 。令
。令
 ,
,
把 代入
代入 中可得
中可得
 。
。
对于(2)式,因为 ,所以
,所以 的原像为
的原像为 ,
, ,
, 的原像为
的原像为 又因为
又因为 不存在完全歧义值,所以存在
不存在完全歧义值,所以存在 使得
使得 。令
。令
 ,
,
把 代入
代入 中可得
中可得
 。
。
5. 定理4的证明
证明:(1) 首先,假设 ,则存在
,则存在 ,使得
,使得 。等式
。等式 在
在 中没有解,与
中没有解,与 相矛盾,故
相矛盾,故 。
。
(2) 其次,假设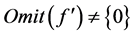 且存在
且存在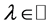 ,使得
,使得 是
是 的一个完全歧义值。如果
的一个完全歧义值。如果 可以对角化,因为
可以对角化,因为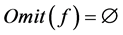 ,则存在矩阵
,则存在矩阵 使得
使得 。否则,
。否则, 与一个Jordan标准型相似,即存在非奇异矩阵
与一个Jordan标准型相似,即存在非奇异矩阵 及
及 ,使得(1)或(2)成立。
,使得(1)或(2)成立。
对于(1)式,如果存在非奇异矩阵 及
及 ,使得
,使得 ,则
,则
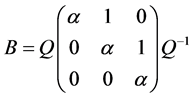 。
。
因为 是
是 的一个完全歧义值, 则
的一个完全歧义值, 则 。把
。把 代入到
代入到 中得
中得
 ,
,
整理得
 。
。
从而
 ,
,
可知上述等式矛盾。
对于(2)式,如果存在非奇异矩阵 及
及 ,使得
,使得 ,则
,则
 。
。
因为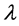 是
是 的一个完全歧义值,则
的一个完全歧义值,则 。进一步得
。进一步得
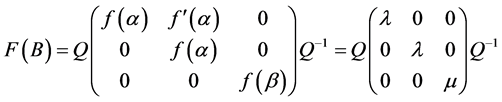 ,
,
整理得
 。
。
从而
 ,
,
可知上述等式也是矛盾的。
当 不可对角化时,
不可对角化时,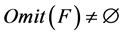 ,所以假设不成立,故
,所以假设不成立,故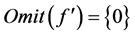 或
或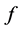 不存在完全歧义值。
不存在完全歧义值。
6. 定理5的证明
证明:(1) 假定 ,设
,设 ,由定理4的证明可知
,由定理4的证明可知 中的矩阵都不可对角化,所以
中的矩阵都不可对角化,所以 不可对角化。则存在非奇异矩阵
不可对角化。则存在非奇异矩阵 及
及 使得(1)或(2)成立。
使得(1)或(2)成立。
因为 ,则存在
,则存在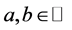 使得
使得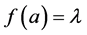 ,
, 又因为
又因为 ,则
,则 。
。
对于(1)式,我们考虑充分大的 ,并且定义曲线
,并且定义曲线 即
即
 。
。
把 代入到
代入到 中可得
中可得
 ,
,
进一步取极限得
 。
。
利用上述的证明方法,类似地可以证明(2)式也是满足的。
(2) 假定 ,其中
,其中 。设
。设 ,根据一维单复变函数中的渐近值
,根据一维单复变函数中的渐近值
理论可知对于充分大的 存在曲线
存在曲线 使得
使得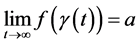 。下面分4种情形讨论。
。下面分4种情形讨论。
情形1:如果 是可对角化矩阵且
是可对角化矩阵且 不是矩阵
不是矩阵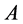 的谱,则
的谱,则 。
。
情形2:如果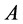 是可对角化矩阵且
是可对角化矩阵且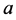 是矩阵
是矩阵 的谱,则存在非奇异矩阵
的谱,则存在非奇异矩阵 及
及 ,使得
,使得
 ,
,
且 ,
, 。因为
。因为 ,则存在
,则存在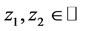 使得
使得 ,
,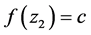 。我们考虑充分大的
。我们考虑充分大的 ,并且定义曲线
,并且定义曲线 即
即
 。
。
把 代入到
代入到 中可得
中可得
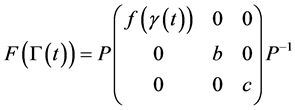 ,
,
进一步取极限得
 。
。
对于其它类型的
 和
和
证明与上述证明类似。
情形3:如果 不可对角化且
不可对角化且 不是矩阵
不是矩阵 的谱,则此情形的证明与(1)相同。
的谱,则此情形的证明与(1)相同。
情形4:如果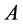 不可对角化且
不可对角化且 是矩阵
是矩阵 的谱,则存在非奇异矩阵
的谱,则存在非奇异矩阵 使得
使得
 。
。
通过对渐近曲线 做细微的改变使得
做细微的改变使得 上没有临界点。我们考虑充分大的
上没有临界点。我们考虑充分大的 ,并且定义曲线
,并且定义曲线 即
即
 。
。
把 代入到
代入到 中可得
中可得
 ,
,
进一步取极限得
 。
。
对于另一种类型的
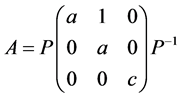 ,
,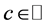
证明是类似的。
7. 定理6和定理7的证明
定理6的证明 设 。由引理1和引理2,我们只需要证明
。由引理1和引理2,我们只需要证明 在
在 中稠密即可。设
中稠密即可。设 ,则存在非奇异矩阵
,则存在非奇异矩阵 使得
使得
 。
。
由引理4可知 是
是 的所有斥性周期点的闭包, 则对任意的
的所有斥性周期点的闭包, 则对任意的 ,存在周期为
,存在周期为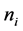 的周期点
的周期点 ,其中
,其中 ,使得
,使得 。进行迭代得
。进行迭代得

令
 ,
,
则
 。
。
定理7的证明 假设 ,则
,则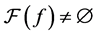 。如果
。如果 是周期Fatou分支里的吸性域,由引理1和引理2我们只考虑可对角化情形。令
是周期Fatou分支里的吸性域,由引理1和引理2我们只考虑可对角化情形。令

其中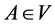 ,
,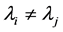 ,
, ,
,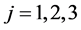 。由
。由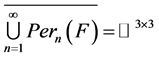 可知,在
可知,在 的
的 邻域内存在周期为
邻域内存在周期为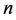 的周期矩阵
的周期矩阵 。由
。由 的矩阵结构可得
的矩阵结构可得 的谱
的谱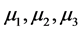 是互不相同的且
是互不相同的且 是可对角化矩阵,则存在非奇异矩阵
是可对角化矩阵,则存在非奇异矩阵 使得
使得

根据引理3矩阵谱的连续性结果可得 。又由吸性域的性质可知
。又由吸性域的性质可知 不是周期矩阵,矛盾。对于其它类型的Fatou周期分支和游荡分支的证明类似。
不是周期矩阵,矛盾。对于其它类型的Fatou周期分支和游荡分支的证明类似。
基金项目
国家自然科学基金资助项目(11571049)。
文章引用
付 超,宋宁芳. 一类全纯矩阵函数的解析性质
The Analyticity Properties of a Class of Holomorphic Matrix Functions[J]. 理论数学, 2016, 06(03): 227-237. http://dx.doi.org/10.12677/PM.2016.63036
参考文献 (References)
- 1. Ahlfors, L.V. (1978) Complex Analysis. 3rd Edition, McGraw-Hill, New York, 307.
- 2. Hayman, W.K. (1964) Me-romorphic Functions. Clarendon Press, Oxford, 78.
- 3. Eremenko, A. and Yu Lyubich, M. (1992) Dynamical Proper-ties of Some Classes of Entire Functions. Annales De L’Institut Fourier, 42, 4. http://dx.doi.org/10.5802/aif.1318
- 4. 杨乐. 值分布理论及其新研究[M]. 北京: 科学出版社, 1982.
- 5. Rosay, J.-Pi. and Rudin, W. (1988) Holomorphic Maps from to . Transactions of the American Mathematical Society, 310, 47-86.
- 6. Fu, C., Li, Y.Z. and Yao, X. (2016) A Note for Picard Theorem for Holomor-phic Matrix-Value Maps in . Complex Analysis and Operator Theory.
- 7. Horn, R.A. and Johnson, C.R. (2012) Matrix Analysis. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9781139020411
- 8. Misiurewicz, M. (1981) On Iterates of . Ergodic Theory and Dynamical Systems, 1, 103-106. http://dx.doi.org/10.1017/S014338570000119X
- 9. Zhan, X.Z. (2002) Matrix Inequalities. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/b83956
- 10. Schleicher, D. (2010) “Dynamics of Entire Functions” Holomorphic Dynamical Systems. Springer-Verlag, Berlin, 295-339. http://dx.doi.org/10.1007/978-3-642-13171-4_5
- 11. 任福尧. 复解析动力系统[M]. 上海: 复旦大学出版社, 1997: 183-202.