Advances in Applied Mathematics
Vol.06 No.09(2017), Article ID:23167,8
pages
10.12677/AAM.2017.69142
Two-Stage Method of Sparse Principal Component Analysis
Xin Yang
The School of Mathematics and Systems, Beihang University, Beijing
Received: Dec. 1st, 2017; accepted: Dec. 19th, 2017; published: Dec. 26th, 2017

ABSTRACT
In this paper, we propose a sparse principal component based on two-stage method, that is, we first get principal component, and then add the regular term of the loadings. Coordinate descent method is used to solve the model. The model is easy to understand. In addition, this paper proposes a heuristic algorithm which can determine the penalty parameters in the model. By selecting the appropriate penalty parameters, the sparse principal component explained variance and sparsity can be optimized at the same time.
Keywords:Dimension Reduction, Sparse Principal Component Analysis, Least Absolute Shrinkage and Selection Operator, Coordinate Descent Method
稀疏主成分分析的两阶段法
杨欣
北京航空航天大学数学与系统科学学院,北京
收稿日期:2017年12月1日;录用日期:2017年12月19日;发布日期:2017年12月26日

摘 要
本文提出稀疏主成分分析的两阶段法,即先求解主成分,然后添加 正则化项得到稀疏载荷,并利用坐标下降法求解模型。方法简单易操作。另外,本文还提出了一种可以确定两阶段模型中惩罚参数的算法,通过选取合适的惩罚参数,可以使稀疏主成分方差和主成分相关性等性能指标取得折衷。
关键词 :降维,稀疏主成分分析,最小迭代收缩阈值和选择算子,坐标下降法

Copyright © 2017 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
多数情况下多指标问题中不同的指标之间有一定的相关性。指标较多加上指标之间的相关性,势必增加了问题分析的复杂性。主成分分析(Principal Component Analysis, PCA)就是一种通过降维技术把多个变量简化为少数几个互不相关的主成分的统计分析方法,主成分是原始变量的线性组合,同时能最大程度上保留原始数据的信息(信息含量用方差表示)。
由于主成分是原始变量的线性组合,并且主成分载荷元素通常非零 [1] ,因此很难对单个主成分做出解释。稀疏主成分分析(Sparse Principal Component Analysis, SPCA)就是为了解决这一缺陷而提出的方法,通过增加主成分载荷中零元素个数,使得主成分可以用最少且最有代表性的变量的线性组合来表示。
为了得到稀疏主成分,研究者们做了很多尝试。Cadima等 [1] 利用硬阈值法,将主成分载荷中绝对值小于给定阈值的元素截断为0,提高了主成分的可解释性,但是这种方法给出的主成分容易识别错误的原始变量。Hausman [2] 将载荷的取值固定在离散集中,例如{-1,0,1},但是该方法得到的载荷稀疏性并不理想,并且稀疏主成分的方差大大减小。2003年I.T.Jolliffe [3] 受LASSO [4] 的启发,直接将 范数约束引入到主成分模型当中,得到的SCoTLASS算法,该算法是第一个基于优化的稀疏PCA算法,但是该算法得到的主成分方差并不理想。在此之后又陆续出现了利用 范数作为约束和 范数、 范数作为惩罚项的稀疏PCA模型及算法。
本文提出稀疏主成分分析的两阶段法,第一阶段得到主成分,第二阶段为了得到稀疏主成分,利用LASSO [4] 问题可以使得回归系数自动缩减为0的特点,将稀疏主成分求解表述为LASSO问题,并用坐标下降法CD [5] [6] 求解该模型,方法简单易操作。此外,本文给出了一种有效确定惩罚参数的方法,利用该算法可以得到合适的惩罚参数,使得主成分各性能指标取得折衷。
下面列出本文中常用的符号术语。
符号 表示 维实数空间, 表示 阶实对称矩阵。 表示符号算子。加粗小写字母表示一个向量,下标表示其分量,向量 的第 个分量用 表示,同样地,加粗大写字母表示一个矩阵,矩阵 的第 个列向量用 表示。符号 表示向量 的 范数。符号 。符号 表示 的软阈值算子。符号 ,其中 表示矩阵的迹。 表示 阶单位矩阵。数据矩阵用 表示,已中心化(列均值为0),样本协方差矩阵 ,其中 表示变量个数, 表示样本数量。
2. 稀疏主成分分析的两阶段法
本节简单说明与两阶段法密切相关的SPCA模型及算法与LASSO模型。
2.1. LASSO问题与SPCA算法
回顾LASSO问题 [4]
其中 表示数据矩阵, 而 是相应的观测值, 是控制 稀疏性的非负参数, 通过选取合适的参数 可以得到满足稀疏性要求的向量解 。
Zou等 [7] 2012年提出SPCA模型,SPCA模型先将PCA表述为回归优化问题,然后添加关于回归系
数的 正则项,即
(1)
其中正参数 控制载荷 的稀疏性。对于 的数据集,要求 前的参数 ;对于 的数据集,取 。
SPCA利用块坐标下降法将(1)的变量分成 和 两个坐标块,固定其中一个坐标块,求解关于另一个坐标块的子问题,交替求解关于两个变量的子问题直至满足终止条件。SPCA模型将PCA与回归分析建立联系,并且对于不同的数据类型( 或 )都具有较低的计算复杂度 [7] 。
SPCA算法初值 均取前 个主成分载荷 ,固定 求解问题(1)等价于求解
(2)
令 ,求解(2)等价于求解 个独立的弹性网问题
(3)
2.2. 两阶段法的第一阶段与第二阶段
稀疏PCA的两阶段法第一阶段需要求得主成分,通常有两种方法可以得到主成分。
(1) 样本协方差阵特征值分解
由于实际数据中总体协方差阵未必已知,因此用样本协方差阵代替总体协方差阵。对样本协方差阵 做特征值分解,并将特征值降序排列,那么前 大特征值对应的特征向量即为前 个主成分载荷 ,对应的主成分表示为 。
(2) 数据矩阵奇异值分解
假设数据矩阵 有SVD分解为 ,其中 , , 是对角线元素为 的对角矩阵, , 的列均标准正交。令 的对角线元素降序排列,在等式 两边同时乘以矩阵 ,得到 ,即矩阵 的列向量为主成分, 的列向量为对应的主成分载荷。不难看出,由于 ,则经过数据矩阵 的奇异值分解得到的 的列向量也是样本协方差矩阵 的特征向量。
将第一阶段得到的前 个主成分表示为 。为了得到稀疏主成分,利用LASSO [4] 问题可以使得回归系数自动缩减为0的特点,用稀疏主成分 拟合主成分 ,得到 个LASSO问题,即
可以看出这 个LASSO问题相互独立,因此只需要给出第一个LASSO问题的算法,其余 问题以此类推。不失一般性,省略 的下标,用 表示。
(4)
分别求解 次问题(4),可以得到前 个稀疏载荷 。
可以看到,问题(4)和(3)相差 这一项,但是在求解 稀疏PCA问题时,通常令 。因此(4)是SPCA准则(1)第一次迭代时所求解的 个子问题。由于SPCA算法同时需要以主成分载荷作为初值,因此这部分计算量与两阶段法第一阶段计算量相同,其次两阶段法的第二阶段是分别求解 个子问题,而SPCA需要交替求解关于变量 和 的子问题,因此计算量要大于两阶段法,第3节的数值结果也证实了这一点。
问题(4)是一个标准LASSO [4] 问题,从而使用经典的求解(3)的算法来求解。文献 [7] 中利用内点法进行求解,但针对基因数据等大规模数据,内点法计算时间过大,效率低下。由于坐标下降法 [6] 能够充分利用高维数据的稀疏特性,已经成为处理大规模稀疏数据的首选算法。因此,本文选择坐标下降法求解问题(4)。
2.3. 基于LASSO的坐标下降法
坐标下降法 [5] 在当前点处沿一个坐标方向进行一维搜索,同时固定其他坐标方向,求解目标函数的局部极小值。在给出坐标下降法求解问题(4)之前,先给出命题1。
命题1:对于任意的 , 表示函数 的最小值点,其中 表示软阈值算子,即
将坐标下降法运用到两阶段法模型(4)。针对 的第 个分量 求解问题(4),同时固定 的值不变,即相当于求解
其中 。根据命题1,得出该子问题的解为
(5)
因此坐标下降法的第 步迭代即为(6)。文献 [5] 中称这种更新方法为平凡更新(naïve updating),并给出了该方法的计算复杂度为 。
对于 的数据集,显然平凡更新计算量很大,因此 [5] 中还给出了另一种协方差更新(covariance up dating)方法,即令
(6)
文献 [5] 中给出该方法的计算度仅为 , 显然对于 的数据集,后一种迭代方法计算复杂度更小。算法终止条件选取迭代次数小于最大迭代次数,或者目标函数值的更新率低于给定阈值,将求解(4)的算法称为TSPCA。
2.4. 参数选择算法
LASSO问题中的非负惩罚参数通常使用交叉验证 [3] 进行确定,但是这种方法高度依赖于数据矩阵,在已知样本协方差矩阵的数据集中,交叉验证的方法并不适用,因此本文提出一种有效的参数选择方法。稀疏度用 表示,下面给出参数选择算法1。
为了说明算法1的执行过程,以Pitprop数据为例。Pitprop数据包含180个样本,13个变量, ,实验提取Pitprop数据前6个稀疏主成分,即令 。图1是利用算法1得到Pitprop数据前6个主成分稀疏度(sparsity)与可解释方差百分比(PEV)函数图(见图1)。
从图1分析可知,Pitprop数据前6个稀疏主成分最佳稀疏度分别是8,11,9,9,12,11,相应的参数分别0.20,0.21,0.4,0.3,0.29,0.56,利用算法1得到了最佳参数。
3. 数值结果
本节将通过三组实验数据验证两阶段法的有效性和可行性,为了观察两阶段法(Two-stage method for Sparse PCA, TSPCA)得到的主成分不相关性和载荷非正交性,将TSPCA数值结果与SPCA [7] 和ALSPCA [8] 进行对比,为了观察TSPCA得到的主成分可解释方差,将TSPCA算法结果与GPower [9] 进行对比,其中SPCA算法代码由本文作者编写,GPower和ALSPCA算法代码则分别下载自作者主页1。实验数据集包括Pitprop数据集,结肠癌基因数据集,20新闻组数据集。所有数值实验均在处理器为因特尔四核2.60Hz的计算机上运行,所需代码利用Matlab2012b软件编写。
实验性能指标选择稀疏度,载荷非正交性 [8] ,稀疏主成分相关性 [8] 及PEV [7] 、计算时间,其中计算时间用来测试TSPCA算法处理大规模稀疏PCA问题的效率,均以秒为单位;稀疏度指的是稀疏载荷中零元素个数(当元素绝对值小于0.001时,即看作是零)。最大迭代次数控制为1000,更新率阈值取作1e-4,初始点 取主成分载荷,惩罚参数 均利用算法1进行选取。
3.1. Pitprop数据
本节利用Jeffers [10] 1967年引进的Pitprop数据测试TSPCA算法表现,它是主成分存在解释困难最为经典的数据集。Pitprop数据包含180个样本,13个变量,即 ,且前6个主成分载荷中没
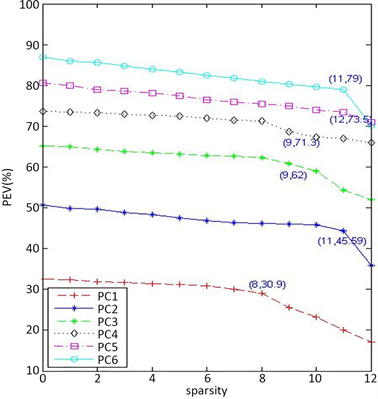
Figure 1. Six PCs of pitprop data: trade-off curve
图1. Pitprop数据:前6个稀疏主成分稀疏度随可解释方差百分比变化图
有零元素,因此本实验只提取前6个稀疏主成分。基于该数据,运行各稀疏PCA算法。根据算法1,TSPCA惩罚参数 如2.4节所述。表1是Pitprop数据下PCA与各稀疏PCA算法的性能指标。
从表1比较发现,当载荷稀疏度相同,TSPCA算法的PEV均高于除GPower以外的其他算法;在主成分相关性和载荷正交性方面,除了ALSPCA算法和SPCA算法之外,TSPCA算法得到的稀疏主成分相关性最小;从计算时间的角度,TSPCA所用时间均比其他算法更短,综合来看,TSPCA算法有一定的竞争力。
以下两组实验是观察TSPCA解决大规模稀疏PCA问题的表现。
3.2. 结肠癌基因数据
结肠癌基因表达数据集 [11] 是大规模高维低样本数据,包含62个样本(22个正常组织样本和40个癌变组织样本)和2000个基因表达变量,即 。由于前3个主成分的PEV大于60%,因此本节抽取结肠癌基因数据前3个主成分。先将数据矩阵中心化。基于该数据,运行各稀疏PCA算法。利用算法2,TSPCA算法前3个惩罚参数均取 。表2是结肠癌基因数据下PCA与各稀疏PCA算法的性能指标。
从表2可以看出,TSPCA算法所得的载荷在保持高稀疏度的情况下,虽然主成分PEV低于其他算法,但是TSPCA算法需要更少的计算时间,并且在非正交性和相关性方面表现也优于除ALSPCA以外的其他算法,验证了本文两种算法在解决高维稀疏PCA问题的简单有效。
3.3. 20新闻组数据
本节所用的20新闻组数据,记录了100个单词出现在16,242篇新闻报导的频次,即 。所有的新闻报导均从全球最大的电子布告栏系统Usenet上取得。该数据下载自 http://blog.csdn.net/imstudying/article/details/77876159#OLE_LINK2。
基于该数据,运行各稀疏PCA算法,并抽取前两个稀疏主成分载荷的数据结果进行对比。对于
Table 1. Six sparse PCs of pitprop data: test index of sparse PCA algorithms
表1. Pitprop数据前6个稀疏主成分:各稀疏PCA算法的性能指标
Table 2. Three sparse PCs of colon cancer data: Test index of sparse PCA algorithms
表2. 结肠癌基因数据前3个稀疏主成分:各稀疏PCA算法的性能指标
Table 3. Two sparse PCs of 20 news group data: test index of sparse PCA algorithms
表3. 结肠癌基因数据前3个稀疏主成分:各稀疏PCA算法的性能指标
TSPCA算法,利用算法2取惩罚参数 。表3为20新闻组数据下PCA和各稀疏PCA算法的性能指标。
从表3可以看出,TSPCA算法所得的载荷PEV虽然略低于其他算法,但是在非正交性和正交性的表现要优于GPower算法;就计算时间而言,TSPCA算法用时最短,进一步验证了本文算法在解决大规模稀疏PCA问题方面的有效性。
4. 结论
本文首次提出稀疏PCA的两阶段法,并利用坐标下降法求解该模型,其次还提出一种可以选取最佳惩罚参数的方法。模型简单易懂,算法易于实现,同时两阶段法每次迭代的计算复杂度关于样本个数 和变量维数 都是线性的,因此可以有效求解大规模稀疏PCA问题,同时惩罚参数选取算法可以有效选取惩罚参数,使得载荷稀疏度和稀疏主成分可解释方差等指标取得折衷。
致谢
衷心感谢指导老师和各位评阅人的建议!
文章引用
杨 欣. 稀疏主成分分析的两阶段法
Two-Stage Method of Sparse Principal Component Analysis[J]. 应用数学进展, 2017, 06(09): 1174-1181. http://dx.doi.org/10.12677/AAM.2017.69142
参考文献 (References)
- 1. Cadima, J. and Jollife, I.T. (1995) Loading and Correlations in the Interpretation of Principal Components. Journal of Applied Statistics, 22, 203-214.
https://doi.org/10.1080/757584614 - 2. Hausman, R. (1982) Constrainted Mul-tivariate Analysis in Optimization in Statistics. North Holland, Amsterdam, 137-151.
- 3. Jolliffe, I.T., Trendafilov, N.T. and Uddin, M. (2003) A Modified Principal Component Technique Based on the LASSO. Journal of Computational and Graphical Statistics, 12, 531-547.
https://doi.org/10.1198/1061860032148 - 4. Tibshirani, R. (1996) Regression Shrinkage and Selection via Lasso. Journal of the Royal Statistical Society, Series B (Methodological), 58, 267-268.
- 5. Hastie, T., Tibshirani, R. and Wainwright, M. (2016) Statistical Learning with Sparsity. A Chapman & Hall Book.
- 6. Hsieh, C.J., Chang, K.W., Lin, C.J., et al. (2008) A Dual Coordinate Descent Method for Large-Scale Linear SVM. Proceedings of the 25th International Conf on Machine Learning, ACM, New York, 408-415.
- 7. Zou, H., Hastie, T. and Tibshirani, R. (2012) Sparse Principal Component Analysis. Journal of Computational and Graphical Statistics, 15, 265-286.
https://doi.org/10.1198/106186006X113430 - 8. Lu, Z. and Zhang, Y. (2012) An Augmented Lagrangian Approach for Sparse Principal Component Analysis. Mathematical Programming, 135, 149-193.
https://doi.org/10.1007/s10107-011-0452-4 - 9. Journee, M., Nesterov, Y. and Richtarik, P. (2010) Generalized Power Method for Sparse Principal Component Analysis. The Journal of Machine Learning Research, 11, 517-553.
- 10. Jeffers, J.N.R. (1967) Two Case Studies in the Application of Principal component Analysis. Applied Statistics, 16, 225-236.
https://doi.org/10.2307/2985919 - 11. Alon, U., Barkai, N., Notterman, D.A., et al. (1999) Broad Patterns of Gene Expression Revealed by Clustering of Tumor and Normal Colon Tissues Probed by Oligonu-cleotide Arrays. Proceedings of the National Academy of Sciences of the United States of America, 96, 6745-6750.
https://doi.org/10.1073/pnas.96.12.6745
NOTES
1GPower算法代码下载自http://www.inma.ucl.ac.be/~richtarik. ALSPCA算法代码下载自http://www.math.sfu.ca/~zhaosong.
