Pure Mathematics
Vol.07 No.01(2017), Article ID:19462,6
pages
10.12677/PM.2017.71002
Generalization and Application of Impulse Integral Inequality with Power
Changqing Liu*, Zizun Li
School of Mathematics and Statistics, Baise University, Baise Guangxi

Received: Dec. 19th, 2016; accepted: Jan. 2nd, 2017; published: Jan. 5th, 2017
Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
In this paper, we give the upper bounds estimation of unknown function with power of impulse integral inequality. The result is used to estimate the upper bound of impulsive differential systems.
Keywords:Impulse Integral Inequalities, Estimation of Unknown Function, Impulsive Differential Systems

含Power的脉冲积分不等式的推广与应用
柳长青*,李自尊
百色学院数学与统计学院,广西 百色

收稿日期:2016年12月19日;录用日期:2017年1月2日;发布日期:2017年1月5日

摘 要
本文研究了含有幂次的脉冲积分不等式,给出了未知函数的上界估计。利用此结果估计了脉冲微分系统的上界。
关键词 :脉冲积分不等式,未知函数估计,脉冲微分系统

1. 引言
Gronwall-Bellman型积分不等式是研究微分方程和积分方程的重要工具,通过对积分不等式中未知函数的估计,可以研究某些微分方程解的存在性、有界性、唯一性和稳定性等定性性质(例如,文献 [1] - [17] )。通过对脉冲积分不等式中未知函数进行估计,可以研究某些脉冲微分方程和解的一些性质。2013年严勇 [16] 研究了含有时滞的脉冲积分不等式

2015年米玉珍,钟吉玉 [13] 研究了含有未知函数的复合函数的积分不等式

其中,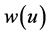 是定义在
是定义在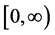 上的单调不减连续函数且当
上的单调不减连续函数且当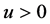 时,
时,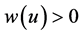 。
。
本文在上述研究成果的基础上,研究了一类含有power的脉冲积分不等式
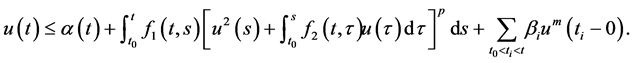 (1.1)
(1.1)
其中,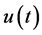 是
是 上只有第一类不连续点
上只有第一类不连续点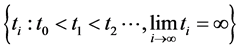 的非负逐段连续函数,
的非负逐段连续函数,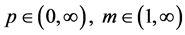 以及
以及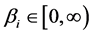 都是给定的常数。
都是给定的常数。
2. 主要结论
假设:
 是定义在
是定义在 上的连续函数,且
上的连续函数,且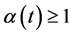 ;
;
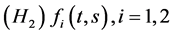 是定义在
是定义在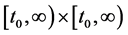 上的非负连续函数;
上的非负连续函数;
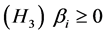 是常数。
是常数。
定理2.1:具有第一类不连续点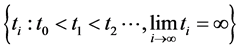 的非负逐段连续函数
的非负逐段连续函数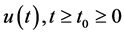 满足积分不等式(1.1),则函数
满足积分不等式(1.1),则函数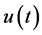 有下面的估计式:
有下面的估计式:
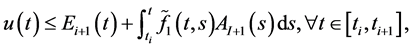
其中
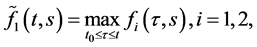


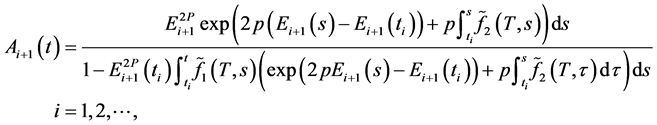

证明:首先,我们考虑情况 ,任取
,任取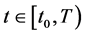 ,可得
,可得

令
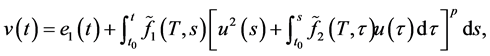 (2.1)
(2.1)
则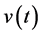 为非负不减的连续函数,且
为非负不减的连续函数,且
 (2.2)
(2.2)
对式(2.1)求导,我们可得
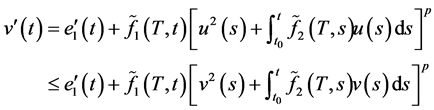 (2.3)
(2.3)
令

则 ,由
,由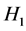 中
中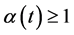 ,得
,得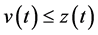 ,对
,对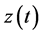 求导,由(2.3)可得
求导,由(2.3)可得
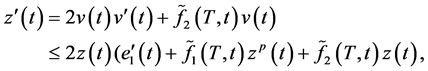 (2.4)
(2.4)
由(2.4)得
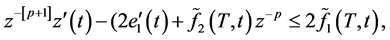 (2.5)
(2.5)
令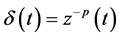 ,则
,则 ,(2.5)可变为
,(2.5)可变为
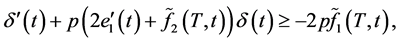 (2.6)
(2.6)
(2.6)两边同时乘以 ,可得
,可得
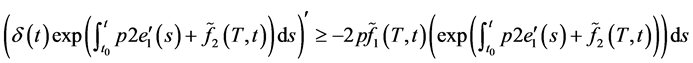 (2.7)
(2.7)
从 到
到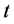 积分(2.7)的两边,我们得到
积分(2.7)的两边,我们得到
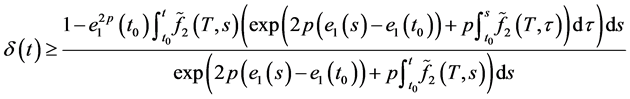 (2.8)
(2.8)
由公式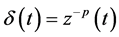 和(2.8)得
和(2.8)得
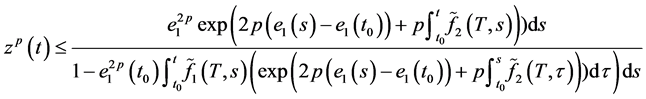 (2.9)
(2.9)
令 等于(2.9)的右边,由(2.3)和(2.9)得
等于(2.9)的右边,由(2.3)和(2.9)得
 (2.10)
(2.10)
(2.10)两边从 到
到 积分得
积分得
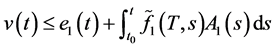 (2.11)
(2.11)
由(2.2)和(2.11)可得
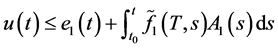 (2.12)
(2.12)
由T的任意性,可得当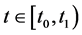 时有
时有
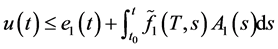 (2.13)
(2.13)
当 时我们证明了估计式。
时我们证明了估计式。
当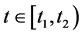 时,任意取定
时,任意取定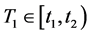 ,对于任意的
,对于任意的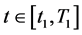 ,不等式(1.1)变为
,不等式(1.1)变为
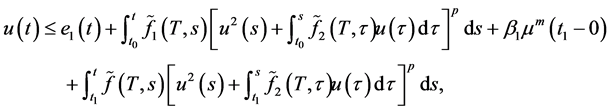 (2.14)
(2.14)
令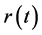 表示(2.14)的右边,且令
表示(2.14)的右边,且令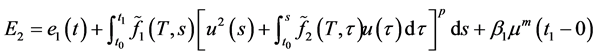 ,则
,则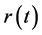 是单调不减函数,且有
是单调不减函数,且有
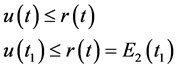 (2.15)
(2.15)
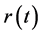 两边关于t求导得
两边关于t求导得
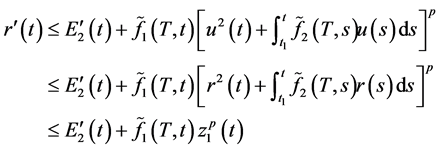 (2.16)
(2.16)
其中 ,(2.16)化为了(2.3)的形式,用相同的过程可得估计式为
,(2.16)化为了(2.3)的形式,用相同的过程可得估计式为
 (2.17)
(2.17)
我们证明了当 时估计式成立。
时估计式成立。
同理,对任意自然数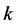 ,当
,当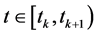 时,我们可以得到未知函数的估计式
时,我们可以得到未知函数的估计式
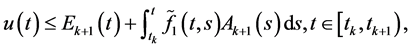 (2.18)
(2.18)
综上定理被证明。
3. 在脉冲微分方程中的应用
本节我们用得到的结果给出脉冲微分系统解的上界估计。考虑脉冲微分系统
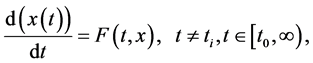 (3.19)
(3.19)
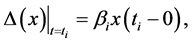 (3.20)
(3.20)
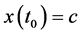 ,
,
其中: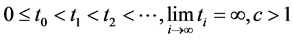 是常数,
是常数,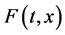 关于
关于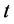 ,
,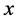 在
在 上连续。
上连续。
假设(3.19)中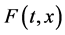 满足
满足
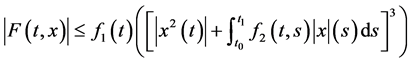 (3.21)
(3.21)
其中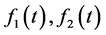 是
是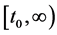 上连续的非负函数。
上连续的非负函数。
推论1:在条件(3.21)成立的情况下,系统(3.19),(3.20)所有的解 满足估计式:
满足估计式:
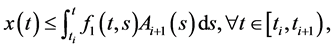 (3.22)
(3.22)
其中




证明:脉冲微分方程(3.19)与(3.20)等价于积分方程
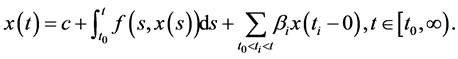 (3.23)
(3.23)
利用条件(3.21),由(3.23),可得
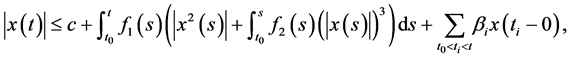 (3.24)
(3.24)
令 ,由(3.24),我们可得不等式
,由(3.24),我们可得不等式
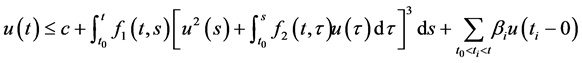 (3.25)
(3.25)
我们看出(3.25)是(1.1)的特殊形式。且(3.25)中的函数满足定理2.1的条件,由定理2.1,我们可以推出 的估计式(3.22)。
的估计式(3.22)。
基金项目
国家自然科学基金项目(11561019);广西自然科学基金项目(2013GXNSFAA019022);广西教育厅项目(201204LX423, 2013LX148, KY2015YB280)。
文章引用
柳长青,李自尊. 含Power的脉冲积分不等式的推广与应用
Generalization and Application of Impulse Integral Inequality with Power[J]. 理论数学, 2017, 07(01): 10-15. http://dx.doi.org/10.12677/PM.2017.71002
参考文献 (References)
- 1. Abdeldaim, A. (2016) Nonlinear Retarded Integral Inequalities of Gronwall-Bellman Type and Applications. Journal of Mathematical Inequalities, 10, 285-299. https://doi.org/10.7153/jmi-10-24
- 2. Agarwal, R.P., Deng, S. and Zhang, W. (2005) Generalization of a Retarded Gronwall-Like Inequality and Its Applications. Applied Mathematics and Computation, 165, 599-612. https://doi.org/10.1016/j.amc.2004.04.067
- 3. Borysenko, S.D. (1983) About Asymptotical Stability on Linear Approximation of the Systems with Impulse Influence. Ukrainian Mathematical Journal, 35, 144-150.
- 4. Borysenko, S.D. (2004) About One Integral Inequality for Piece-Wise Continuous Functions. Proceedings of X International Kravchuk Conference, Kyiv, 323.
- 5. Borysenko, S.D., Ciarletta, M. and Iovane, G. (2005) Integro-Sum Inequalities and Motion Stability of Systems with Impulse Perturbations. Nonlinear Analysis, 62, 417-428. https://doi.org/10.1016/j.na.2005.03.032
- 6. Gllo, A. and Piccirilo, A.M. (2007) About New Analogies of Gronwall-Bellman-Bihari Type Inequalities for Discontinuous Functions and Estimated Solutions for Impulsive Differential Systems. Nonlinear Analysis, 67, 1550-1559. https://doi.org/10.1016/j.na.2006.07.038
- 7. Gllo, A. and Piccirilo, A.M. (2009) About Some New Generalizations of Bell-man-Bihari Results for Integro-Func- tional Inequalities with Discontinuous Functions and Applications. Nonlinear Analysis, 71, e2276-e2287. https://doi.org/10.1016/j.na.2009.05.019
- 8. Iovane, G. (2007) Some New Integral Inequalities of Bellman-Bihari Type with Delay for Discontinuous Functions. Nonlinear Analysis, 66, 498-508. https://doi.org/10.1016/j.na.2005.11.043
- 9. 李自尊. 脉冲积分不等式未知函数的估计[J]. 四川师范大学学报(自然科学版), 2013, 36(2): 258-262.
- 10. 柳长青, 李自尊. 一类新的非连续函数积分不等式及其应用[J]. 理论数学, 2013(3): 4-8.
- 11. 孟东沅. 一类新型不连续函数的积分不等式及应用[J]. 数学的实践与认识, 2009(39): 161-166.
- 12. Mi, Y.Z., Deng, S.F. and Li, X.P. (2013) Nonlinear Integral Inequalities with Delay for Discontinuous Functions and Their Applications. Journal of Inequalities and Applications, 2013, 11 p.
- 13. 米玉珍, 钟吉玉. 非连续函数的Bellman-Bihari型积分不等式的推广[J]. 四川大学学报(自然科学版), 2015, 52(1): 33-38.
- 14. Wang, W.S. (2007) A Generalized Retarded Gronwall-Like Inequality in Two Variables and Applications to BVP. Applied Mathematics and Computation, 191, 144-154. https://doi.org/10.1016/j.amc.2007.02.099
- 15. Wang, W.S. and Li, Z.Z. (2011) A New Class of Impulsive Integral Inequalities and Its Application. 2011 International Conference on Multimedia Technology (ICMT 2011), 3, 1897-1899. https://doi.org/10.1109/ICMT.2011.6002439
- 16. 严勇. 一类带脉冲项的Gronwall-Bellman型积分不等式的推广及应用[J]. 四川师范大学学报(自然科学版), 2013, 36(4): 603-609.
- 17. Zheng, Z.W., Gao, X. and Shao, J. (2016) Some New Generalized Retarded Inequalities for Discontinuous Functions and Their Applications. Journal of Inequalities and Applications, 2016, 14 p.
NOTES
*通讯作者。