ABSTRACT

In this paper we study the s-Convex Functions of the second type. We show that a master theorem holds for the s-Convex Functions, and we then apply it to obtain Ky-Fan type inequalities and Milne type inequalities.

Keywords:Convex Functions, S-Convex Functions of the Second Type, Master Theorem, Milne Type Inequalities, Ky-Fan Type Inequalities

关于第二类s-凸函数的注记

李耀文¹，张沂昀²

¹南京大学数学系，江苏 南京

²南京大学大学外语部，江苏 南京

收稿日期：2016年1月26日；录用日期：2016年2月13日；发布日期：2016年2月18日

摘 要

本文中，我们研究了第二类s-凸函数，把凸函数的子母定理推广到s-凸函数的相应形式，由此证明了Ky-Fan型不等式，Milne型不等式。

关键词 :凸函数，第二类s-凸函数，子母定理，Milne型不等式，Ky-Fan型不等式

1. 引言

在文献[1] 中，H. Hudzik与L. Maligranda考察了以下的一类函数：

定义：固定某个，对于，如果函数满足：

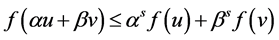
那么称如果函数为第二类s-凸函数，记为。以下简称s-凸函数。

关于s-凸函数，我们有如下一些性质：(参见文献[2] 、[3] )

(1) 若，函数为s-凸函数，则函数在 上非负。

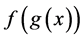(2) 若f是单调非减的s-凸函数，g是上非负的凸函数，则复合函数也是s-凸函数。

(3) 若f是φ-函数及s-凸函数，g是上的φ-函数及凸函数，则复合函数也是s-凸函数。特别地，是s-凸函数。这里一个函数h被称为φ-函数是指函数、连续、单调非减，并且。

(4) 假设函数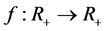是s-凸函数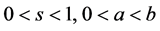，，f在上可积，那么如下Hermite-Hadamard型不等式成立：

显然正的凸函数是s-凸函数；是s-凸函数；由性质(2)、(3)可以从已知的s-凸函数得到新的s-凸函数。另外Dragomir和Pearce(见[2] ，pp. 288-292中的定理190、191)还证明了所谓的F-映射与H-映射都保持s-凸性质，由此派生出一些s-凸函数，但是关于s-凸函数非平凡的例子所知不多，我们甚至不知道简单的形如的s-凸函数。如何给出新例子，是值得研究的问题。另外s-凸函数在概率论的研究中也有重要应用。

另一方面，我们有如下的关于凸函数的子母定理：

定理A(见[3] [4] )：假设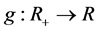是严格凸函数，并且由所定义，那么对任意正实数与，不等式成立，且其中等式成立当且仅当序列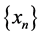与成比例。

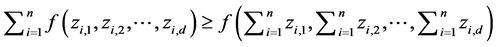定理B(见[4] )：假设是严格凸函数，并且由所定义，那么对任意正实数构成的矩阵，不等式成立，且其中等式成立当且仅当矩阵的秩为1。

对于凹函数，以上两个定理中的结论反向。

我们将给出关于s-凸函数类似的子母定理，并由此证明了Ky-Fan型不等式，Milne型不等式。

2. 关于s-凸函数的子母定理

定理2：假设，函数是s-凸函数，如果由所定义，那么对任意正实数与，不等式成立。

证明：只需对n=2情形证明。由于g是s-凸函数，我们有

所以定理成立。

与凸函数情形不同，在s-凸函数的子母定理中，等式成立一般不能得出两组正实数成比例。

类似地，我们定义多元函数是s-凸函数，如果对某个固定，不等式

对于都成立。当时，s-凸函数就是通常意义下的正值凸函数。对正值凸函数有

在时成立，所以多元函数正值凸函数都是s-凸函数，但是反之未必对，正值凹函数也有可能是s-凸函数。我们知道多元函数为凸函数当且仅当它的Hesse矩阵是正定的，某函数的Hesse矩阵正定可以推论函数s-凸。类似于一元情形，容易证明多元函数的子母定理。

定理3：假设是s-凸函数，由所定义，那么对任意正实数构成的矩阵，成立以下不等式：

。

3. 定理的应用

定理4：对任意正实数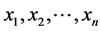与, 在时以下不等式都成立：

(1) Ky-Fan型不等式：，这里已假设。

(2) Cauchy-Schwarz不等式：。

(3) 对任意正实数，与，成立如下Milne型不等式：

。

(4) 对任意正实数，与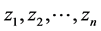，成立如下Milne型不等式：

。

证明：

(1) 由于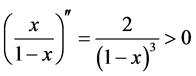，，当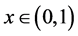，是凸函数，显然也是-函数，由性质(3)可知是s-凸函数。由定理2，即满足Ky-Fan型不等式。注：经典的Ky-Fan不等式是这里的不等式一个特殊情况。

(2) 由于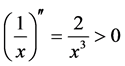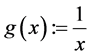，是凸函数，所以也是s-凸函数。由定理2，即满足次线性不等式：，我们令，此式化为Cauchy-Schwarz不等式。注：这里的不等式是一个已知的结果。

(3) 由于对于，我们可以计算二元函数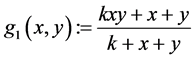的Hesse矩阵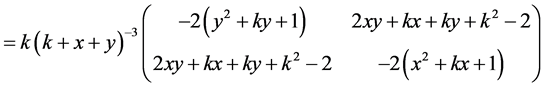，其行列式，矩阵是负定的，所以函数是严格凹函数。由定理B，对应的函数满足超线性不等式：

又由于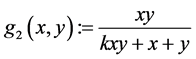的Hesse矩阵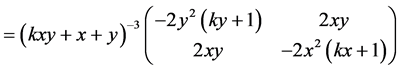对于易见是负定的，所以函数是严格凹函数。由定理B，对应的函数满足超线性不等式：

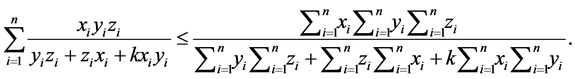
将上述两个不等式相乘即证得结论。由定理B，对应的等式成立时，对应的三组正数成比例。

注：当k=1时，这里的不等式就是文献[4] 中的Milne不等式。

(4) 由于的Hesse矩阵显然是正定的，所以是严格凸函数，也是s-凸函数。由定理3，对应的函数满足次线性不等式：

又由于的Hesse矩阵易见它是正定的，所以此函数也是s-凸函数。由定理3，对应的函数满足次线性不等式：

将上述两个次线性不等式相乘即证得。

致谢

本文第一作者受国家自然科学基金No-11071112部分资助，以及受南京大学匡亚明学院教改项目部分资助，以及受中央高校基本科研业务费专项资金资助。第二作者受南京大学翻转课堂项目部分资助，特此致谢。另外，作者对审稿人有益的建议表示感谢。

文章引用

李耀文,张沂昀. 关于第二类s-凸函数的注记
A Note on s2-Convex Functions[J]. 运筹与模糊学, 2016, 06(01): 10-14. http://dx.doi.org/10.12677/ORF.2016.61002

参考文献 (References)