Operations Research and Fuzziology
Vol.06 No.03(2016), Article ID:18462,8
pages
10.12677/ORF.2016.63011
A Study of the Zoonotic Infectious Disease Model
Lijuan Zhang, Fuchang Wang, Yibin Zhao
Institute of Disaster Prevention Science and Technology, China Earthquake Administration, Sanhe Hebei

Received: Aug. 9th, 2015; accepted: Aug. 28th, 2016; published: Aug. 31st, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
This paper established a zoonotic infectious disease model with livestock population containing latent period and there is infectiousness in the latent period. The model considered the influence of strain variation for human and controlling the disease through hunting of the livestock with disease. We also discussed the stability of the disease-free equilibrium and the basic reproduction number of the system. By means of computer simulation, this paper studied the impact of parameters such as hunting coefficient, immune, etc. on diseases.
Keywords:Mathematic Model, the Loss of Immunity, Global Stability, Basic Reproduction Number

一类人畜共患的传染病模型的研究
张丽娟,王福昌,赵宜宾
中国地震局,防灾科技学院,河北 三河

收稿日期:2015年8月9日;录用日期:2016年8月28日;发布日期:2016年8月31日

摘 要
本文建立了一类畜类群体含潜伏期且潜伏期内有传染性的人畜共患传染病模型。该模型考虑了人感染变异毒株的影响,考虑了对患病畜类捕杀的策略来控制疾病,并讨论了无病平衡点的稳定性,以及系统的基本再生数。通过计算机仿真研究了捕杀系数以及免疫等参数对疾病的影响。
关键词 :数学模型,疫苗免疫丧失,全局稳定性,基本再生数

1. 模型建立
疫苗注射和捕杀是在控制诸如H5N1类病毒、狂犬病等在畜类种群中传播的主要策略。然而,考虑到伦理、生态以及经济等因素捕杀不是最好的选择 [1] [2] 。因此,疫苗注射便成为大多数国家普遍采取的策略。一般,疫苗注射不会在种群中产生完全免疫,需要考虑从时间以及注射疫苗种类不同,会有免疫力丧失的情况出现,在数学模型中主要用免疫失效率来描述 [3] [4] 。
埃博拉疫情的蔓延使人类更加认识到人畜共患的传染病模型更加符合实际情况。在国外,Nyuk Sian Chong等 [5] 研究了一类人鸟共患的流感模型,讨论了基本再生数的敏感性,以及平衡点的稳定性。然而并未考虑潜伏期、疫苗注射、适度捕杀等因素的影响,而在国内在此方面的研究几乎没有。另外,关于感染率很多模型中用了多种形式 [5] [6] ,线性发生率主要针对于各人群均匀混合,每一位患病者以相同概率感染易感者,主要应用在诸如鸡痘、霍乱、流感等传染病 [7] 。如果人群是拥挤和饱和状态时,饱和发生
率效果较好 [8] 。在本文,考虑半饱和发生率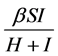 ,
, 是感染率,
是感染率, 是半饱和常数。
是半饱和常数。
本文研究人畜共患模型中畜类分为易感者、疫苗注射者、潜伏期、发病者四类群体。人类分为易感者、感染者、感染变异菌株者、移出者四类,建立模型如下:
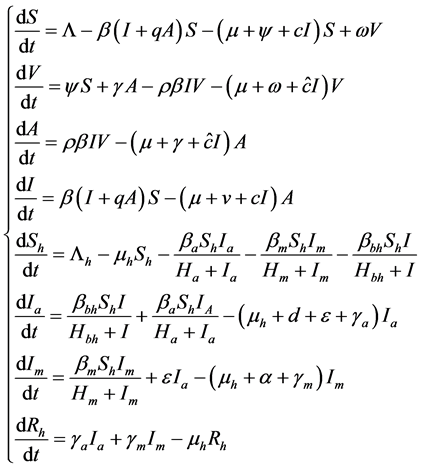 (1)
(1)
其中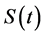 为易感者畜类在时刻
为易感者畜类在时刻 的数量;
的数量; 为增长率(包括迁入者以及新出生者);
为增长率(包括迁入者以及新出生者); 为疫苗注射免疫的数量;
为疫苗注射免疫的数量; 为畜类患病数量;
为畜类患病数量;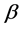 为感染率;
为感染率; 为畜类平均死亡率;
为畜类平均死亡率; 为因病死亡率;
为因病死亡率;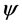 为疫苗注射率;
为疫苗注射率;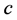 对易感以及患病畜类捕杀率;
对易感以及患病畜类捕杀率;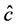 为注射疫苗及潜伏期畜类捕杀率;
为注射疫苗及潜伏期畜类捕杀率; 为疫苗丧失率;
为疫苗丧失率;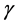 潜伏期畜类恢复率;
潜伏期畜类恢复率; 为由于疫苗注射对感染率抑制系数;
为由于疫苗注射对感染率抑制系数;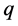 为潜伏期畜类感染率抑制系数;
为潜伏期畜类感染率抑制系数; 为病毒变异致死率;
为病毒变异致死率; 为易感人群
为易感人群 时刻数量;
时刻数量;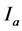 为感染正常菌株人群在
为感染正常菌株人群在 时刻数量;
时刻数量; 为感染变异菌株的人群
为感染变异菌株的人群 时刻数量;
时刻数量;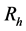 为康复人群在
为康复人群在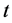 时刻数量;
时刻数量;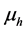 为人均死亡率;
为人均死亡率;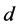 为因病死亡率;
为因病死亡率;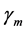 为感染变异菌株人群死亡率;
为感染变异菌株人群死亡率;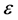 为感染者转变为变异菌株的比率;
为感染者转变为变异菌株的比率; 为感染正常菌株的恢复率;
为感染正常菌株的恢复率; 为感染率(下标
为感染率(下标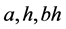 分别表示正常菌株、变异菌株、交叉感染率);
分别表示正常菌株、变异菌株、交叉感染率);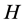 为半饱和常数(下标
为半饱和常数(下标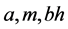 分别表示正常菌株、变异菌株、人畜交叉感染);
分别表示正常菌株、变异菌株、人畜交叉感染);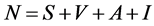 ;
; 。
。
2. 系统适定性
模型中所有参数都是非负的,因此须证明对所有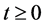 时,系统的变量全为非负。
时,系统的变量全为非负。

因此,几何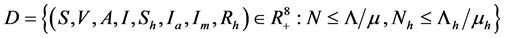 。是系统的是适定区域。
。是系统的是适定区域。
引理1:闭集 是有界正不变的。
是有界正不变的。
证明:由于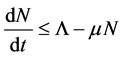 ,
, 以
以 为上界,得
为上界,得
 ,
, 。
。
同理可得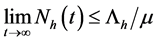 。因此,可得
。因此,可得 是有界正不变集。
是有界正不变集。
3. 禽类模型分析
设 。系统无病平衡点为
。系统无病平衡点为 ,其中
,其中 ,
, ,容易求得其基本再生数为
,容易求得其基本再生数为 。
。
引理2:若 ,则系统没有地方病平衡点,若
,则系统没有地方病平衡点,若 则系统有一个唯一的地方病平衡点。
则系统有一个唯一的地方病平衡点。
证明:平衡点为以下方程的根
 (2)
(2)
由上式方程可得 将其代入第二个方程得到
将其代入第二个方程得到
因此, ,由第四个方程可得
,由第四个方程可得
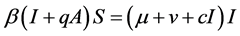 ,
,
将以上两式代入第一个方程得
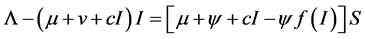 。
。
 ,因此有
,因此有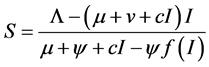 ,
, ,且
,且 关于
关于 是减函数,因此
是减函数,因此 关于
关于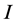 也是不减的,对于
也是不减的,对于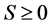 成立。代入最后一个方程
成立。代入最后一个方程
 。
。
令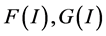 分别为上式的左端和右端,由
分别为上式的左端和右端,由 关于
关于 单调递减,因此,
单调递减,因此,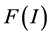 关于
关于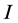 是减函数。
是减函数。 关于
关于 是线性增加的,若两函数相交,必然交于点
是线性增加的,若两函数相交,必然交于点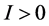 ,是地方病平衡点存在的必要条件,充分必要条件是
,是地方病平衡点存在的必要条件,充分必要条件是 。
。
 ,
,
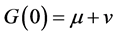 .
.
通过计算可得 。
。
为证明系统地方病平衡点稳定性,令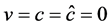 。
。
定理1:当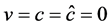 时,若
时,若 ,地方病平衡点是局部渐进稳定的。
,地方病平衡点是局部渐进稳定的。
证明:设地方病平衡点为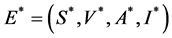 ,
, 的雅克比矩阵为
的雅克比矩阵为
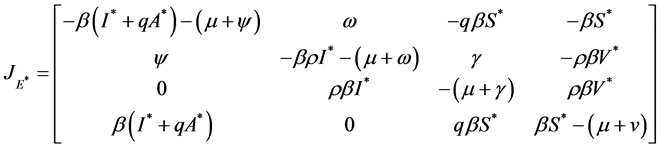
令 并定义
并定义 ,则有
,则有
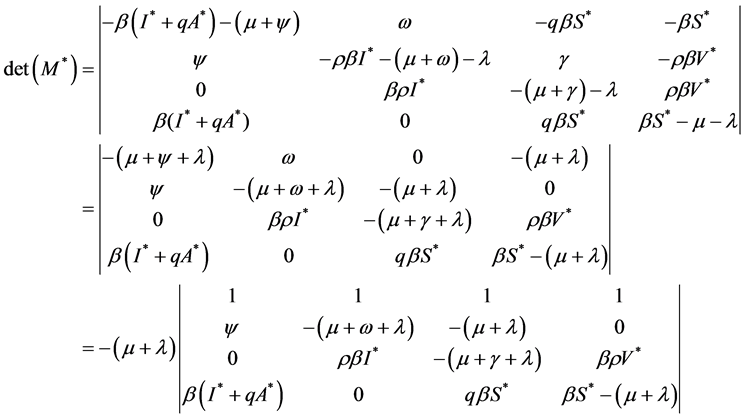
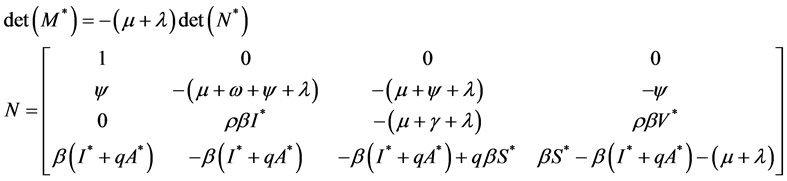
可得特征方程:

其中, ,
, ,
,
 ,
,
 。
。
由方程(2)最后一个等式可得 。由(2)式中第三个等式可得
。由(2)式中第三个等式可得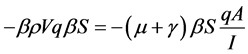 。因此可得
。因此可得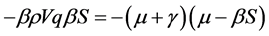 。代入
。代入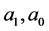 知:
知:


由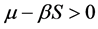 ,因此
,因此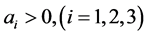 。接下来,要证
。接下来,要证 。由已知得
。由已知得 。由(2)式可得,可得
。由(2)式可得,可得
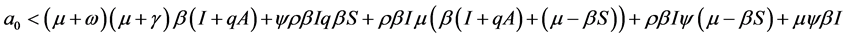 。
。
令上式右侧为 ,
,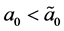 ,易得
,易得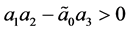 ,因此,由Routh-Hurwitz判别法可知地方病平衡点是局部渐进稳定的。
,因此,由Routh-Hurwitz判别法可知地方病平衡点是局部渐进稳定的。
4. 系统基本再生数
由Diekmann [9] ,令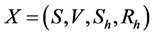 (没有被感染的人数),
(没有被感染的人数),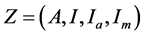 (被感染且具有传染性的个体),无病平衡点
(被感染且具有传染性的个体),无病平衡点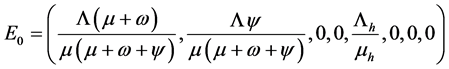 。
。

其中
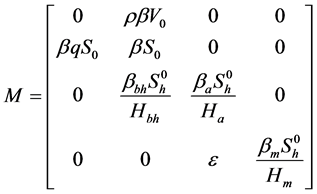 ,
,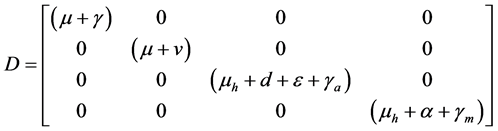
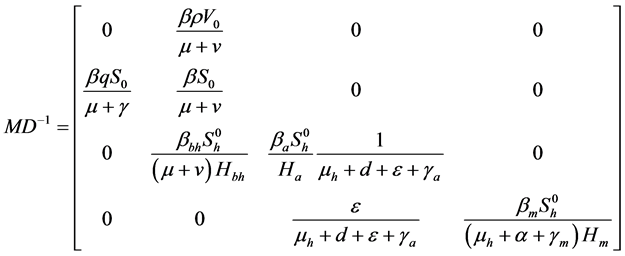
 。
。
因为字块 的特征方程为:
的特征方程为:

可知其特征根 ,
, ,因此,
,因此, 异号,其正根定比
异号,其正根定比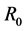 。
。
5. 系统仿真
为验证理论正确性,本文取参数

此时基本再生数为1.4754,系统中畜类患病比率以及人群中患病人数如图1,从图中可以看到畜类患病比率以及人群患病人数趋于稳定。
改变参数值,取参数:

此时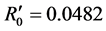 ,各患病比率如图2。
,各患病比率如图2。
取参数




Figure 1. Proportion of the diseased population
图1. 各患病群体比率




Figure 2. Proportion of the diseased population
图2. 各患病群体比率

此时 ,各患病群体比率如图3,从图中可以看到系统是不稳定的,人类患病比率呈直线
,各患病群体比率如图3,从图中可以看到系统是不稳定的,人类患病比率呈直线
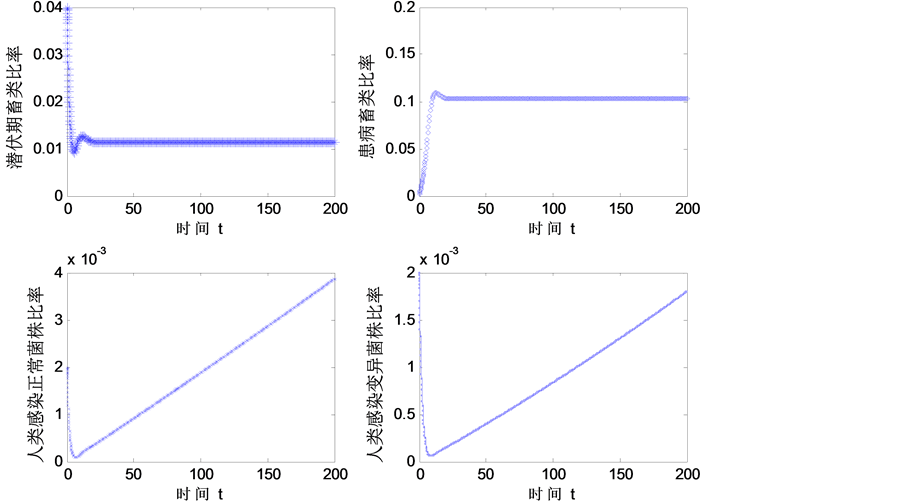
Figure 3. Proportion of the diseased population
图3. 各患病群体比率
上升,因此当系统不稳定时对人类的影响是显著的。
6. 结论
本文建立了一类人畜共患的传染病模型,对模型进行了基本再生数及稳定性分析,并仿真的办法对系统中各变量变化趋势进行了模拟。该模型参数较多,只对其中部分参数进行了讨论,还有一些工作需要进行开展,作者将在以后的工作中继续对该类模型进行进一步研究。
文章引用
张丽娟,王福昌,赵宜宾. 一类人畜共患的传染病模型的研究
A Study of the Zoonotic Infectious Disease Model[J]. 运筹与模糊学, 2016, 06(03): 85-92. http://dx.doi.org/10.12677/ORF.2016.63011
参考文献 (References)
- 1. Food and Agriculture Organization (2007) Avian Influenza Vaccination. OEI Information Document. http://www.oie.int/downld/AVIAN%20INFLUENZA/Guidelines%20on%20AI%20vaccination.pdf
- 2. Food and Agriculture Organization (2011) Animal Intervention Strategies under Different Epidemiological and Field Conditions That Can Deduce Risk of Zoonotic Infection. OFFLU Review Paper. http://www.who.int/influenza/resources/research/2010_04_29_global_influenza_research_agenda_version_01_en.pdf
- 3. Brauer, F. (2004) Backward Bifurcations in Simple Vaccination Models. Journal of Mathematical Analysis and Applications, 298, 418. http://dx.doi.org/10.1016/j.jmaa.2004.05.045
- 4. Heffernab, J.M. and Keeling, M.J. (2009) Implications of Vaccination and Waning Immunity. Proceedings of the Royal Society B, 276, 2071-2080. http://dx.doi.org/10.1098/rspb.2009.0057
- 5. Chong, N.S., Tchuenche, J.M. and Smith, R.J. (2014) A Mathe-matical Model of Avian Influenza with Half-Saturated Incidence. Theory in Biosciences, 133, 23-38.
- 6. Kaddar, A. (2010) Stability Analysis in a Delayed SIR Epidemic Model with a Saturated Incidence Rate. Nonlinear Analysis: Modelling and Control, 15, 299-306.
- 7. Du, Y. and Xu, R. (2010) A Delayed SIR Epidemic Model with Nonlinear Incidence Rate and Pulse Vaccination. Journal of Applied Mathematics and Informatics, 28, 1089-1099.
- 8. Gao, S., Chen, L., Nieto, J.J. and Torres, A. (2006) Analysis of a Delayed Epidemic Model with Pulse Vaccination and Saturation Incidence. Vaccine, 24, 6037-6045. http://dx.doi.org/10.1016/j.vaccine.2006.05.018
- 9. Diekmann, O. and Yakubu, A.A. (2002) Mathematical Approaches for Emerging and Reemerging Infectious Diseases: An Introduction. IMA Volumes in Mathematics and its Applications, Vol. 125, Springer, Heidelberg, 229-250. http://dx.doi.org/10.1007/978-1-4757-3667-0_13