ABSTRACT

In this paper, the sufficient and necessary conditions of nonnegative Hamilton matrix are proved. Secondly, the problem of when the algebraic index of the eigenvalue of a class of Hamilton matrix is one is studied and the sufficient conditions are given.

Keywords:Hamilton Matrix, Eigenvalues, Eigenvectors, Algebraic Index

一类Hamilton矩阵特征值的代数指标

吴永霞^*，吴德玉^*，王媋瑗，董瑞婷，沈易，向民

内蒙古大学，数学科学学院，内蒙古 呼和浩特

收稿日期：2018年2月22日；录用日期：2018年3月7日；发布日期：2018年3月14日

摘 要

本文首先证明了非负Hamilton矩阵可逆的充分必要条件。其次研究了一类Hamilton矩阵特征值的代数指标何时为1的问题，并给出了特征值的代数指标为1的充分条件。

关键词 :Hamilton矩阵，特征值，特征向量，代数指标

Copyright © 2018 by authors and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

英国数学家W. R. Hamilton根据光学与力学之间的深刻联系，对经典力学进行了创造性的研究得到了与Newton力学、Lagrange力学等价的又一种力学表述——Hamilton力学。Hamilton力学以其严谨、对称的数学框架成为经典力学史上的美妙理论，并最终成为量子力学等许多学科的理论基础。量子力学创始人薛定谔曾说“Hamilton原理已成为现代物理的基石，如果想要用现代理论解决任何物理问题，首先得把它表示成Hamilton形式” [1] 。Hamilton系统是Hamilton力学的数学表示，它在数学、物理和力学领域具有广泛应用。有限维线性Hamilton系统是Hamilton系统里最简单且最基本的形式，该系统对应的系数矩阵为如下形状的 $2n\times 2n$ 矩阵：

$H=\left[\begin{array}{cc}A& B\\ C& -A^{\ast }\end{array}\right],$

其中 $B,C$ 是Hermite矩阵， $A^{*}$ 是的共轭转置，此时称 $H$ 为Hamilton矩阵。Hamilton矩阵的特征值问题以及可逆性问题在代数方程求解问题、控制论以及辛几何等领域有重要应用 [2] 。

据我们所知，矩阵特征值的代数重数与几何重数在研究矩阵若当标准型、对角化以及在可修复系统，向量型Sturm-Liouville问题，迁移理论等领域也具有重要应用。一般情况下，矩阵的代数重数与几何重数不一定相等。但是，当特征值的代数指标为1的时候，代数重数与几何重数相等，此时不存在广义特征向量。因此本文研究了Hamilton矩阵特征值的代数指标何时为1的问题，给出了Hamilton矩阵特征值的代数指标何时为1的一些充分条件。

2. 预备知识

为了证明主要结论首先给出下列定义及引理。

定义1：设 $D\in C^{n\times n}$ 为Hermite矩阵，如果对任意的 $0\ne x\in C^n$ 都有

$x^{*}Dx>0\left(x^{*}Dx\ge 0\right),$

则称 $D$ 为Hermite正定矩阵(半正定矩阵) [3] 。

定义2：分块矩阵 $H=\left[\begin{array}{cc}A& B\\ C& -A^{*}\end{array}\right]$ ，则其中 $B,C$ 是Hermite矩阵， $A^{*}$ 是 $A$ 的共轭转置，此时称 $H$ 为Hamilton矩阵。如果是Hermite半正定矩阵，则称 $H$ 为非负Hamilton矩阵 [4] 。

定义3：设 $\lambda \in C$ ，使得

$N^K\left(D,\lambda \right)=N^{K+1}\left(D,\lambda \right),$

成立的最小的非负整数 $K$ 称为 $\lambda$ 的代数指标，记为 $P_{\lambda }\left(D\right)$ ，其中

$N^K\left(D,\lambda \right)=\left\{u|{\left(D-\lambda I\right)}^{K}u=\text{0}\right\}.$

引理1：设 $D$ 是复数域上的 $C^{n\times n}$ 的矩阵，如果对任意的 $u\in N\left(D,\lambda \right)$ 存在 $v\in N^K\left(D^{*},\bar{\lambda }\right)$ 使得，则 $D$ 在 $\lambda$ 处的代数指标不超过 $K$ ，特别的，若 $K=1$ 则 $D$ 在 $\lambda$ 处的代数指标为1。

证明：假定 $P_{\lambda }\left(D\right)=K+1$ ，则存在 $u_{\text{0}}\in N^{K+1}\left(D,\lambda \right)$ 使得

${\left(D-\lambda I\right)}^{K+1}{u}_0=0,{\left(D-\lambda I\right)}^K{u}_0\ne 0,$

即 ${\left(D-\lambda I\right)}^K{u}_{\text{0}}\in N\left(D,\lambda I\right)$ 。根据给定条件，存在 $v\in N^K\left(D^{*},\bar{\lambda }\right)$ 使得

$v^{\text{*}}{\left(D-\lambda I\right)}^K{u}_0\ne 0,$

两边取共轭转置得

$u_0^{\ast }{\left(D^{\text{*}}-\bar{\lambda }I\right)}^{K}v\ne 0,$

这与 $v\in N^K\left(D^{*},\bar{\lambda }\right)$ 矛盾。从而 $P_{\lambda }\left(D\right)\le K$ 。

引理2： $D\in C^{n\times n}$ 是Hermite半正定矩阵，如果存在向量 $x_0$ 使得 $x_0^{*}D{x}_{\text{0}}=0$ ，则 $D{x}_{\text{0}}=0$ 。

证明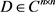：是Hermite半正定矩阵，因此，存在矩阵 $P\in C^{n\times n}$ ，使得 $D=P^{*}P$ ，即得

$x_0^{*}D{x}_0=x_0^{*}{P}^{*}P{x}_0={\left(P{x}_0\right)}^{*}P{x}_0=0,$

故

$P{x}_0=0,$

两边同乘矩阵 $P^{*}$ 得

$P^{*}P{x}_0=D{x}_0=0.$

3. 主要结果及其证明

定理1：设 $H=\left[\begin{array}{cc}A& B\\ C& -A^{*}\end{array}\right]\in C^{2n\times 2n}$ 是非负Hamilton矩阵，则 $H$ 可逆当且仅当

$N\left(A\right)\cap N\left(C\right)=\left\{0\right\}$

且 $N\left(A^{\text{*}}\right)\cap N\left(B\right)=\left\{0\right\}$ 。

证明：必要性。当 $H$ 可逆时，假设 $N\left(A\right)\cap N\left(C\right)\ne \left\{0\right\}$ ，则存在 $x_0\in N\left(A\right)\cap N\left(B\right)$ 使得

$A{x}_0=0,C{x}_0=0.$

令 $u={\left[\begin{array}{cc}{x}_0& 0\end{array}\right]}^{\text{T}}$ ，则有

$\left[\begin{array}{cc}A& B\\ C& -A^{*}\end{array}\right]\left[\begin{array}{c}{x}_0\\ 0\end{array}\right]=\left[\begin{array}{c}A{x}_0\\ C{x}_0\end{array}\right]=0.$

这与 $H$ 可逆矛盾，假设不成立。

同理可证 $N\left(A^{\text{*}}\right)\cap N\left(B\right)\ne \left\{0\right\}$ 时与条件矛盾。由此可得 $H$ 可逆时

$N\left(A\right)\cap N\left(C\right)=\left\{0\right\}$ 且 $N\left(A^{\text{*}}\right)\cap N\left(B\right)=\left\{0\right\}.$

充分性。假设矩阵 $H$ 不可逆，则存在 $u={[\begin{array}{cc}{x}_0& y_0\end{array}]}^{\text{T}}\ne \text{0}$ ，使得

$A{x}_{\text{0}}+B{y}_0=0,C{x}_0-A^{*}{y}_0=0.$ (3.1.1)

第一式两边与 $y_0$ 作内积， $x_{\text{0}}$ 与第二式两边作内积后两式相加得

$x_0^{\ast }C{x}_{\text{0}}+y_0^{\ast }B{y}_0=0,$

由于 $B,C$ 是Hermite半正定矩阵，从而

$x_0^{\ast }C{x}_{\text{0}}=0,y_0^{\ast }B{y}_0=0,$

由引理2可知

$C{x}_0=0,B{y}_0=0,$

进而代入式(3.1.1)得

$A{x}_0=0,-A^{*}{y}_0=0.$

则得出

$C{x}_0=0,A{x}_0=0$

这与条件矛盾。结论证毕。

定理2：设 $H=\left[\begin{array}{cc}A& B\\ C& -A^{*}\end{array}\right]\in C^{2n\times 2n}$ Hamilton矩阵，如果 $B$ 是Hermite正定矩阵且 $B^{-1}A$ 是Hermite矩阵，则对任意 $\text{0}\ne \lambda \in \sigma \left(H\right)$ 有 $P_{\lambda }\left(H\right)=1$ 。其中 $\sigma \left(H\right)$ 表示 $H$ 的特征值集合。

证明：对任意 $u={\left[\begin{array}{cc}x& y\end{array}\right]}^{\text{T}}\in N\left(H,\lambda \right)$ ，考虑到

$Ax+By=\lambda x,Cx-A^{*}y=\lambda y,$

以及 $B$ 是Hermite正定矩阵，有

${\lambda }^2\left(x^{*}{B}^{-1}x\right)+\lambda \left(x^{*}{A}^{*}{B}^{-1}x\right)-\lambda \left(x^{*}{B}^{-1}Ax\right)-\left(x^{*}Cx\right)-\left(x^{*}{A}^{*}{B}^{-1}Ax\right)=0.$

由于 $\left(x^{*}{B}^{-1}Ax\right)\in R$ ，于是

$\lambda \left(x^{*}{A}^{*}{B}^{-1}x\right)-\lambda \left(x^{*}{B}^{-1}Ax\right)=0,$

且 $\sigma \left(H\right)\subset R\cup iR$ 。

当 $\sigma \left(H\right)\subset R$ 时，取 $v=\left[\begin{array}{c}-\lambda B^{-1}x-B^{-1}Ax\\ -x\end{array}\right]$ ，则

$\left(H^{*}-\bar{\lambda }\right)v=\left(H^{*}-\lambda \right)v=J\left(H+\lambda \right)Jv=0,$

其中 $J$ 表示辛矩阵 $J=\left[\begin{array}{cc}0& I_n\\ -I_n& 0\end{array}\right]$ ， $I_n$ 是单位矩阵。此时有

$v{}^{*}u=\left(\left[\begin{array}{c}x\\ \lambda B^{-1}x-B^{-1}Ax\end{array}\right],\left[\begin{array}{c}-\lambda B^{-1}x-B^{-1}Ax\\ -x\end{array}\right]\right)=-2\lambda \left(x^{*}{B}^{-1}x\right)\ne 0,$

由引理1可知， $P_{\lambda }\left(H\right)=1$ 。

当 $\lambda \in iR$ 时，取 $v=\left[\begin{array}{c}-\lambda B^{-1}x+B^{-1}Ax\\ x\end{array}\right]$ ，则

$\left(H^{*}-\bar{\lambda }\right)v=\left(H^{*}+\lambda \right)v=J\left(H-\lambda \right)Jv=0,$

并且

$v^{*}u=\left(\left[\begin{array}{c}x\\ \lambda B^{-1}x-B^{-1}Ax\end{array}\right],\left[\begin{array}{c}-\lambda B^{-1}x+B^{-1}Ax\\ x\end{array}\right]\right)=2\lambda \left(x^{*}{B}^{-1}x\right)\ne 0,$

由引理1可知， $P_{\lambda }\left(H\right)=1$ 。结论证毕。

注：若把定理2的条件改成 $C$ 是Hermite正定矩阵且 $C^{-1}{A}^{*}$ 是Hermite矩阵，则同理可证定理2的结论仍成立。

定理2的条件是对 $\text{0}\ne \lambda \in \sigma \left(H\right)$ 来说的，而 $0=\lambda \in \sigma \left(H\right)$ 时定理2的结论不一定成立。下面给出具体例子说明这一点。

例1：令 $H=\left[\begin{array}{cc}A& B\\ C& -A^{*}\end{array}\right]=\left[\begin{array}{cc}0& I_n\\ 0& 0\end{array}\right]$ 是Hamilton矩阵，则 $B$ 是Hermite正定矩阵且 $B^{-1}A$ 是Hermite矩阵，满足定理2的条件。然而，经计算易得

${\lambda }_1={\lambda }_2=0$

并且

$H^2=\left[\begin{array}{cc}0& I_n\\ 0& 0\end{array}\right]\left[\begin{array}{cc}0& I_n\\ 0& 0\end{array}\right]=\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right]$

取 $u={\left[\begin{array}{cc}\text{0}& x\end{array}\right]}^{\text{T}}\ne 0$ ，其中 $x$ 是 $n$ 维非零向量，则

$Hu={\left[\begin{array}{cc}x& 0\end{array}\right]}^{\text{T}}\ne 0,$

但

$H^{\text{2}}u=0.$

从而得矩阵 $H$ 的 $\lambda =0$ 的代数指标为2。

那么，当 $\lambda =0$ 是Hamilton矩阵 $H$ 的特征值时，代数指标何时为1呢？下面的定理将回答这个问题。

定理3：设 $H=\left[\begin{array}{cc}A& B\\ C& -A^{*}\end{array}\right]\in C^{2n\times 2n}$ Hamilton矩阵，如果 $B$ 是可逆矩阵且Hermite矩阵 $i\left(B^{-1}A-A^{*}{B}^{-1}\right)$ 或 $-i\left(B^{-1}A-A^{*}{B}^{-1}\right)$ 为正定矩阵时，当 $\lambda =0$ 是Hamilton矩阵的特征值时 $P_{\lambda }\left(H\right)=1$ 。

证明：对任意 $u={\left[\begin{array}{cc}x& y\end{array}\right]}^{\text{T}}\in N\left(H\right)$ ，有

$Ax+By=\text{0},Cx-A^{*}y=\text{0},$

得

$u={\left[\begin{array}{cc}x& -B^{-1}Ax\end{array}\right]}^{\text{T}},$

从而

$Ju=\left[\begin{array}{cc}0& I_n\\ -I_n& 0\end{array}\right]\left[\begin{array}{c}x\\ -B^{-1}Ax\end{array}\right]={\left[\begin{array}{cc}-B^{-1}Ax& -x\end{array}\right]}^{\text{T}}\in N\left(H^{*}\right),$

并且

${\left(Ju\right)}^{\text{*}}u=\left(\left[\begin{array}{c}x\\ -B^{-1}Ax\end{array}\right],\left[\begin{array}{c}-B^{-1}Ax\\ -x\end{array}\right]\right)=x^{*}\left(B^{-1}A-A^{*}{B}^{-1}\right)x\ne 0,$

由引理1可知， $P_{\lambda }\left(H\right)=1$ 。结论证毕。

注：若把定理3的条件改成 $C$ 是可逆矩阵且 $i\left(B^{-1}A-A^{*}{B}^{-1}\right)$ 或 $-i\left(B^{-1}A-A^{*}{B}^{-1}\right)$ 为正定矩阵，则同理可证定理3的结论仍成立。

基金项目

内蒙古大学创新创业基金项目(批准号：201711204)，国家自然科学基金(批准号：11561048)。

文章引用

吴永霞,吴德玉,王媋瑗,董瑞婷,沈 易,向 民. 一类Hamilton矩阵特征值的代数指标
Algebraic Index of Eigenvalue of a Class of Hamilton Matrix[J]. 应用数学进展, 2018, 07(03): 243-248. https://doi.org/10.12677/AAM.2018.73030

参考文献