International Journal of Mechanics Research
Vol.06 No.04(2017), Article ID:22995,12
pages
10.12677/IJM.2017.64017
Highly Accurate Fox-Goodwin Time Integration Method
Xiuyuan Xing1, Huimin Zhang2
1The High School Affiliated to China University of Mining and Technology (Beijing), Beijing
2Beihang University, Beijing
Received: Nov. 22nd, 2017; accepted: Dec. 6th, 2017; published: Dec. 12th, 2017

ABSTRACT
A Highly Accurate Fox-Goodwin time Integration Method (HAFIM) is presented in this paper. HAFIM creates the highly accurate Jacobi matrix by multi-sub-step notion and uses the highly accurate Jacobi matrix for recursive procedure. In the process of constructing the matrix, the exponential matrix operation techniques are employed to reduce the computational efforts and the computer rounding error. The analysis on properties indicates that the proposed method possesses higher amplitude and phase accuracy compared with the Precise time Integration Methods (PIMs). Moreover, the proposed method is very practical given its simplicity.
Keywords:Fox-Goodwin Method, High Accuracy, Time Integration Method, Precise Integration Method
高精度Fox-Goodwin时间积分法
邢修源1,张慧敏2
1中国矿业大学(北京)附属中学,北京
2北京航空航天大学,北京
收稿日期:2017年11月22日;录用日期:2017年12月6日;发布日期:2017年12月12日

摘 要
本文建立了高精度Fox-Goodwin时间积分法。这种方法采用等分步的思想,连乘每分步的Jacobi矩阵建立高精度Jacobi矩阵,然后利用高精度Jacobi矩阵进行递推求解。在构造高精度Jacobi矩阵的过程中,用指数矩阵运算技巧来达到降低计算量,用存贮增量矩阵策略来减小舍入误差的影响。性能分析表明,这种方法与精细积分法相比,具备较高的幅值和相位精度,且格式简单,便于应用。
关键词 :Fox-Goodwin方法,高精度,时间积分法,精细积分法

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
时间积分法是求解结构动力学响应强有力的方法之一,它的基本思想是将时间域离散,通过迭代格式求出各离散时刻的物理量近似值。经典时间积分法有Houbolt方法 [1] ,Newmark方法 [2] ,Wilson-θ方法 [3] ,Hilber-Hughes-Taylor-α方法 [4] 和Wood-Bossak-Zienkiewicz-α方法 [5] 等,上世纪九十年代以来也出现了诸多新颖的时间方法,例如Zhai方法 [6] ,广义-α方法 [7] ,Bathe方法 [8] 和基于加权残量思想的方法 [9] 等。但这些方法大都只有二阶精度,需要使用非常小的步长才能实现高精度要求,导致大量的计算量。
对于线性定常系统,钟 [10] 提出了精细积分方法(Precise Integration Method, PIM),以其高精度,高效率等优点得到了广泛应用。PIM的基本思想是对微分方程的解析解进行精确数值计算,对于齐次方程,PIM可以给出计算机精度的解。而对于非齐次方程,需要求解非齐次项产生的Duhamel积分,钟 [11] 和林 [12] 就非齐次项分别为多项式、弦函数、指数函数以及它们的组合形式时,推导了相应的精细积分递推格式,后来又发展了很多种非齐次项的积分方法,例如直接对非齐次项Duhamel积分进行数值积分求解 [13] ,或者增维精细积分方法 [14] 等。当用于求解结构动力学响应时,PIM是一种条件稳定算法 [15] ,它的精度会随着展开项的增多而提高。
本文借助PIM中使用的指数矩阵乘法和存储增量的技术,基于Fox-Goodwin方法 [16] 构造高精度时间积分法Highly Accurate Fox-Goodwin time Integration Method (HAFIM)。Fox-Goodwin方法是一种辛几何算法,对于无阻尼系统可实现四阶精度,并且具有足够的稳定区间。对于收敛的算法来说,当步长趋近于0时,数值解趋近于解析解。HAFIM的思想是将每个时间步长N等分,在每一个分步内使用Fox-Goodwin方法,通过连乘每分步的Jacobi矩阵计算出单步的高精度Jacobi矩阵,利用该Jacobi矩阵进行迭代求解。在构造高精度Jacobi矩阵的过程中,2m算法和增量算法分别被用来减少计算量和降低舍入误差。与PIM相比,HAFIM具有更简单的矩阵形式和更优秀的数值性能。
2. 算法格式
2.1. 动力学方程
结构动力学方程的一般形式为
(1)
式中,M,C,K分别为质量,阻尼和刚度矩阵, , ,x分别为加速度,速度和位移向量,R(t)为外部激励。若R(t)可表示为一系列基本函数的组合,且这些函数可以用其本身和一阶和二阶导数线性表出,即
(2)
则可使用增维的方式将外载荷函数转化为待求变量,从而将非齐次方程(1)转化为齐次方程
(3)
式中,I为单位矩阵,O为零矩阵。下面给出最一般的转化方式。
在有限时间内,任意连续函数都可展开成傅里叶级数的形式,则R(t)可近似表示为
(4)
式中,T0为R(t)的基本周期,a0,an和bn为傅里叶系数,q为展开项数。若令
(5)
则任意函数均可近似转化为方程(2)的形式。特别地,如果外激励函数本身是二阶齐次常微分方程的解,如常激励,简谐激励,或它们的组合形式等,方程(2)可严格满足。
基于以上讨论,本文仅关注齐次方程的求解,即
(6)
式中
(7)
2.2. 求解格式
时间积分法求解方程(6)的简明递推格式为
(8)
式中,A为Jacobi矩阵或称为传递矩阵,zk为在时间点 的状态向量,h为时间步长。本文采用Fox-Goodwin方法,其差分格式为
(9)
则对应的Jacobi矩阵为
(10)
HAFIM用多分步的思想,将步长h等分为N份,在每个分步内使用时间积分法,则其递推格式可写为
(11)
式中,AH为高精度Jacobi矩阵,可由各分步的Jacobi矩阵连乘得到,即
(12)
式中,分步长 。在构造AH的过程中,2m算法和增量算法可分别用来减小计算量和计算机舍入误差。
1) 2m算法
取 ,如 , ,则仅需m次迭代就可得到AH,相当于执行下列语句
(13)
2) 增量算法
当hN很小时,A(hN)与单位矩阵十分接近,可写为
(14)
式中,S(hN)为增量矩阵
(15)
可以看出,当hN趋近于0时,S(hN)接近于零矩阵。由于一般台式计算机仅有16位有效数字,S(hN)的精度可能会在迭代过程中丧失殆尽。为避免精度损失,在构造AH的过程中,要单独存储S(hN),而不是A(hN)。又因为
(16)
则需执行的语句变为
(17)
经过m次乘法后,S不再是一个很小的矩阵,此时AH可由下式得到
(18)
综上所述,表1给出了HAFIM求解线性定常系统的执行步骤。在计算过程中,HAFIM与PIM有两处不同:首先,HAFIM直接给出了增量矩阵S(hN)的形式,而PIM的增量矩阵需由系数矩阵进一步计算得到;其次,HAFIM无需对结果进行变换,可直接求得位移、速度和加速度,而PIM的速度和加速度需由进一步变换得到,所以说HAFIM计算更为简便,所需时间成本也更低。
实际上,任意一种时间积分法都可按照同样的方式来构造相应的高精度方法,本文选取Fox-Goodwin方法是由于其具备良好的精度和稳定性,下面我们将说明这种方法的性能优势。
Table 1. Solution procedures of the highly accurate Fox-Goodwin time integration method
表1. 高精度Fox-Goodwin时间积分方法的执行步骤
3. 算法性能
衡量算法性能优劣的指标主要有稳定性和精度两个方面。对于线性定常系统,由于模态正交性,可以通过对单自由度系统问题的分析来说明算法的特性,即振动方程为
(19)
式中,ξ和ω分别为阻尼率和固有频率。为避免参数N的影响,这里仅研究Fox-Goodwin方法本身的性质,并与梯形法则(Trapezoidal-Rule, TR),中心差分法(Central-Difference-Method, CDM)和PIM进行对比。TR和CDM是结构动力学中常用的时间积分法,对无阻尼系统不具有数值阻尼,精度较高。
3.1. 稳定性
稳定性要求算法的谱半径 。对于单自由度方程(19),Fox-Goodwin方法的Jacobi矩阵为
(20)
式中, 。类似地,TR和CDM的Jacobi矩阵分别如下
(21)
(22)
而PIM的性质随着展开项数的增多而不同,这里给出最常用的两种情况:
1) L = 3
(23)
2) L = 4
(24)
式中L表示截断阶数,而
(25)
图1和图2分别给出了无阻尼情况和阻尼率为0.1时这几种方法的谱半径曲线。可以看出,TR为无条件稳定算法,其余方法均为条件稳定方法,Fox-Goodwin方法的稳定区间介于两种精细积分法之间。为方便应用,表2给出了这三种方法的稳定极限τcr,当 时,算法可以给出稳定的结果。
3.2. 精度
考虑单自由度系统(19),该问题的解析解为
(26)
式中,c1和c2为由初始条件确定的常数, 。而数值解的形式为
(27)
式中

Figure 1. Spectral radius ( ξ = 0)
图1. 谱半径曲线( ξ = 0)

Figure 2. Spectral radius ( = 0.1)
图2. 谱半径曲线( = 0.1)
Table 2. The stability limits of these methods
表2. 算法的稳定极限
(28)
在稳定区间内,λ1,2为一对共轭复根。将数值解的形式与解析解对比,我们可以用 来表示数值耗散的程度,称为幅值衰减率。而数值弥散一般用周期延长率来表示,定义为
(29)
图3和图4分别给出了这几种格式的幅值衰减率和周期延长率曲线,结果表明无阻尼情况下,PIM的幅值精度较差,TR和CDM方法的相位精度较差,而Fox-Goodwin方法的幅值和相位精度皆优于其它方法,因此本文选用Fox-Goodwin方法来构造高精度时间积分法。特别地,由于Fox-Goodwin方法的辛几何特性,其幅值衰减率为零,这意味着幅值误差不会随着步数的增多而累积,对长期仿真十分有利。
4. 数值仿真
考虑三自由度无阻尼质点-弹簧系统,如图5所示。弹簧的刚度系统均为k = 1 N/m2,质点的质量均为m = 1 kg,质点1处受到简谐激励R = 10sin5t N作用,系统的运动方程为
(30)
令 ,则方程(28)可转化为齐次方程
(31)
初始条件为
(32)

Figure 3. Amplitude decay ratio ( ξ = 0)
图3. 幅值衰减率曲线( ξ = 0)
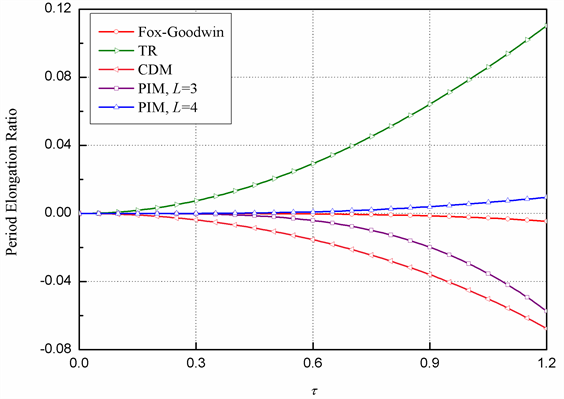
Figure 4. Period elongation ratio ( ξ = 0)
图4. 周期延长率曲线( ξ = 0)
在本例中,由于激励为简谐函数,齐次方程(29)与原方程(28)的解析解完全相同。
简谐激励周期为 ,因此采用的时间步长选为 ,令 ,应用HAFIM和PIM (L = 3, L = 4)计算了该系统在[0, 40 s]内的位移,速度和加速度响应。质点1的结果如图6~8所示,其中精确解由模态叠加法得到。可以看出,由于HAFIM的保辛特性,其幅值误差不累积;而经过一段

Figure 5. Mass-spring system
图5. 质点–弹簧系统

Figure 6. Displacement and the absolute errors of the methods at node 1
图6. 质点1的位移响应和数值方法的绝对误差
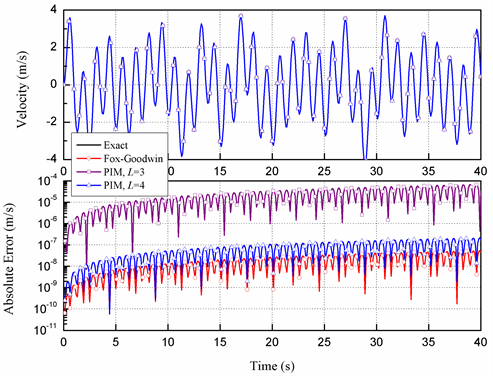
Figure 7. Velocity and the absolute errors of the methods at node 1
图7. 质点1的速度响应和数值方法的绝对误差
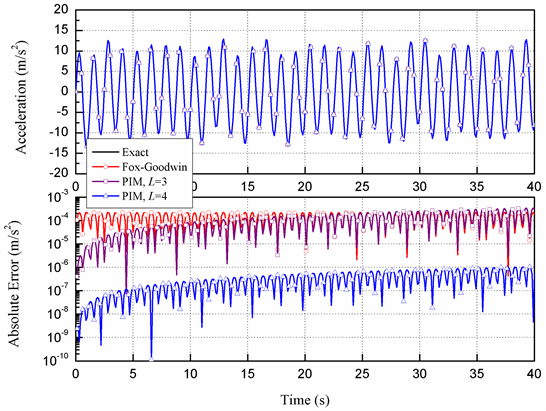
Figure 8. Acceleration and the absolute errors of the methods at node 1
图8. 质点1的加速度响应和数值方法的绝对误差
时间后,PIM的幅值耗散会大大降低结果的精度,尤其是位移和加速度响应更加明显,因此HAFIM对长期仿真十分有利。此外,虽然PIM的位移精度较高,但其速度精度较差,即使是截断到第4阶(L = 4),其速度误差也远大于HAFIM给出的结果。
5. 结论
本文构造了高精度Fox-Goodwin时间积分法。它的基本思想是将每个时间步等分为N份,连乘每个分步的Jacobi矩阵构造高精度Jacobi矩阵,然后使用高精度Jacobi矩阵进行递推求解。在构造高精度Jacobi矩阵的过程中,2m算法和增量算法被用来提升计算效率,减小舍入误差。
相比较于精细积分法来说,本文提出的方法结合了时间积分法本身的优势,使得其在计算量和性能上得到优化。首先,这种方法的增量矩阵无需进一步计算,可采用文中给出的形式,并可直接得到位移和速度的数值解;其次,Fox-Goodwin方法的辛几何特性使得该方法具备较高的幅值精度,且应用于无阻尼系统时是一种四阶格式;最后,数值结果证实了高精度Fox-Goodwin时间积分法的精度优势。
致谢
感谢国家自然科学基金资助项目(批准号为11372021和11672019)的资助。
文章引用
邢修源,张慧敏. 高精度Fox-Goodwin时间积分法
Highly Accurate Fox-Goodwin Time Integration Method[J]. 力学研究, 2017, 06(04): 161-172. http://dx.doi.org/10.12677/IJM.2017.64017
参考文献 (References)
- 1. Houbolt, J.C. (1950) A Recurrence Matrix Solution for the Dynamic Response of Elastic Aircraft. Journal of Aeronautical Science, 17, 540-550. https://doi.org/10.2514/8.1722
- 2. Newmark, N.M. (1959) A Method of Computation for Structural Dynamics. ASCE Journal of the Engineering Mechanics Divisions, 85, 67-94.
- 3. Wilson, E.L. (1968) A Computer Program for Dynamic Stress Analysis of Underground Structures. SESM, University of California, Berkeley.
- 4. Hilber, H.M., Hughes, T.J.R. and Taylor, R.L. (1977) Improved Numerical Dissipation for Time Integration Algorithms in Structural Dynamics. Earthquake Engineering and Structural Dynamics, 5, 283-292. https://doi.org/10.1002/eqe.4290050306
- 5. Wood, W.L., Bossak, M. and Zienkiewicz, O.C. (1980) An Alpha Modification of Newmark’s Method. International Journal for Numerical Methods in Engineering, 15, 1562-1566. https://doi.org/10.1002/nme.1620151011
- 6. Zhai, W.M. (1996) Two Simple Fast Integration Methods for Large-Scale Dynamic Problems in Engineering. International Journal for Numerical Methods in Engineering, 39, 4199-4214. https://doi.org/10.1002/(SICI)1097-0207(19961230)39:24<4199::AID-NME39>3.0.CO;2-Y
- 7. Chung, L. and Hulbert, G.M. (1993) A Time Integration Algorithm for Structural Dynamics with Improved Numerical Dissipation: The Generalized-α Method. Journal of Applied Mechanics, 60, 371-375. https://doi.org/10.1115/1.2900803
- 8. Bathe, K.J. and Baig, M.M.I. (2005) On a Composite Implicit Time Integration Procedure for Nonlinear Dynamics. Computers and Structures, 83, 2513-2524. https://doi.org/10.1016/j.compstruc.2005.08.001
- 9. Zhou, X. and Tamma, K.K. (2004) Design, Analysis, and Synthesis of Generalized Single Step Single Solve and Optimal Algorithms for Structural Dynamics. International Journal for Numerical Methods in Engineering, 59, 597-668. https://doi.org/10.1002/nme.873
- 10. 钟万勰. 结构动力方程的精细时程积分[J]. 大连理工大学学报, 1994, 34(2): 131-136.
- 11. 钟万勰. 暂态历程的精细计算方法[J]. 计算结构力学及其应用, 1995, 12(1): 1-6.
- 12. Lin, J.H., Shen, W.P. and Williams, F.M. (1997) Accurate High-Speed Computation of Nonstationary Random Seismic Response. Engineering Structures, 19, 586-593. https://doi.org/10.1016/S0141-0296(97)83154-9
- 13. 汪梦甫, 周锡元. 结构动力方程的更新精细积分方法[J]. 力学学报, 2004, 36(2): 191-195.
- 14. 顾元宪, 陈飚松, 张洪武. 结构动力方程的增维精细积分法[J]. 力学学报, 2000, 32(4): 447-456.
- 15. Wang, M.F. and Au, F.T.K. (2006) Assessment and Improvement of Precise Time Step Integration Method. Computers and Structures, 84, 779-786. https://doi.org/10.1016/j.compstruc.2006.02.001
- 16. Fox, L. and Goodwin, E.T. (1949) Some New Methods for the Numerical Integration of Ordinary Differential Equations. Proceedings of Cambridge Philosophical Society, 45, 373-388. https://doi.org/10.1017/S0305004100025007
