International Journal of Fluid Dynamics
Vol.05 No.01(2017), Article ID:19880,12
pages
10.12677/IJFD.2017.51002
A Lattice Boltzmann Model for the Steady State Compressible Flows
Bo Yan1, Jianchao Wang1, Guangwu Yan2
1College of Civil Engineering, Jilin Jianzhu University, Changchun Jilin
2College of Mathematics, Jilin University, Changchun Jilin

Received: Feb. 20th, 2017; accepted: Mar. 6th, 2017; published: Mar. 9th, 2017

ABSTRACT
In this paper, a multi-energy-level lattice Boltzmann model for the steady state compressible flows is proposed. Firstly, the Chapman-Enskog expansion and the multi-spatial scale expansion are used to describe the higher-order moment of equilibrium distribution functions and a series of partial differential equations in different spatial scales. Secondly, the modified partial differential equation of the Euler equation with the higher-order truncation error is obtained. Thirdly, comparison between numerical results of the lattice Boltzmann models and exact solution is given. The numerical results agree well with the classical one.
Keywords:Lattice Boltzmann Model, Compressible Flows, Steady State Lattice Boltzmann Equation
一种定常可压缩流动的格子Boltzmann模型
闫铂1,王建朝1,闫广武2
1吉林建筑大学土木工程学院,吉林 长春
2吉林大学数学学院,吉林 长春
收稿日期:2017年2月20日;录用日期:2017年3月6日;发布日期:2017年3月9日

摘 要
本文给出了一种用于定常可压缩流动的多能级格子Boltzmann模型。我们使用Chapman-Enskog展开和空间多尺度展开技术描述平衡态分布函数的高阶矩和不同空间尺度的系列方程,进而得到了具有高阶误差的Euler方程的修正方程。我们还给出了格子Boltzmann模型的数值模拟结果与解析解的比较。结果表明,数值模拟结果与解析解吻合的很好。
关键词 :格子Boltzmann模型,可压缩流动,定常格子Boltzmann方程

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近30年来,格子Boltmzann方法(LBM)已经发展成为一种有效的计算流体动力学(CFD)方法 [1] [2] [3] [4] 。目前,LBM已经广泛应用于多相流 [5] 、多组分流 [6] 、多孔介质流 [7] 、悬浮流 [8] 等复杂问题。此外,LBM可以求解Burgers方程 [9] [10] 、KdV方程 [11] ,Lorenz方程 [12] ,Schrödinger方程 [13] [14] [15] 和Poisson方程 [16] [17] 等线性和非线性偏微分物理方程。
用LBM模拟可压缩流动比较困难,因为LBM模型本身受到低Mach数的限制,其本质是冲量流,与能量相关。近年来,为了消除可压缩流动对低Mach数的限制,提出了大量的LBM模型 [18] - [49] ,这些模型都是用来研究非定常可压缩流动的。
在可压缩流动的研究领域,提出了许多明显细化的有限差分模型 [50] - [54] 。非结构网格有限体积法可以求解复杂边界问题 [50] ;总变差减小(TVD)模型 [51] 和本质不振荡(ENO)模型 [52] 可以减小数值扩散和非物理振荡;无网格法可以跳出对离散网格的限制 [53] ;水平集法(the level set method)可以追踪移动边界 [54] 。然而,这些格式在求解可压缩流动时,会产生高清晰度的激波,其中TVD格式最为明显。而本文提出的LBM模型,是与时间无关的格子Boltzmann模型。与以往的LBM不同,本文所使用的多尺度是空间多尺度。数值结果表明,LBM模拟结果与以上经典解法求得的结果吻合的很好。
2. 格子Boltzmann模型
2.1. 格子Boltzmann方程
首先考虑一个两层正六边形格子,其12个格点分别与中心点相连结。假设粒子沿格线运动,粒子速度 可分解为
可分解为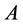 和
和 两部分,每一部分具有不同能级
两部分,每一部分具有不同能级 和
和 ,静止粒子
,静止粒子 的能级为
的能级为 。即,该速度模型是25结点3速度
。即,该速度模型是25结点3速度 模型,
模型, ,
, 、
、 分别为空间步长和时间步长。
分别为空间步长和时间步长。 (
(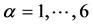 和
和 );
);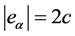 (
( 和
和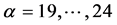 ),
), ,如图1所示。
,如图1所示。
定义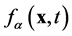 为
为 位置,t时刻的分布函数,其速度为
位置,t时刻的分布函数,其速度为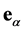 ,则每个位置的宏观质量、动量和能量分别为
,则每个位置的宏观质量、动量和能量分别为
 , (1)
, (1)
 , (2)
, (2)
 , (3)
, (3)

 (a) (b)
(a) (b)
Figure 1. Schematic of lattice. (a) type A, (b) type B
图1. 格子示意图。(a) A型,(b) B型
在公式(3)中, 为单位质量的内能。
为单位质量的内能。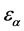 为能级[41],且具有三个值
为能级[41],且具有三个值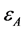 ,
, 和
和 。则定常格子Boltzmann方程 [55] [56] 可表示为
。则定常格子Boltzmann方程 [55] [56] 可表示为
 (4)
(4)
其中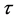 是松弛因子,
是松弛因子, 是
是 位置的局部平衡态分布函数,其速度为
位置的局部平衡态分布函数,其速度为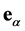 。设平衡态分布函数
。设平衡态分布函数 具有如下形式
具有如下形式

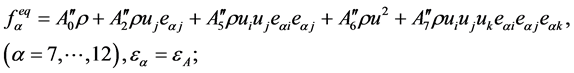
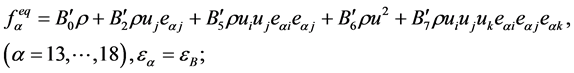


其中 、
、 、
、 、
、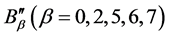 ,
, 是由质量守恒、动量守恒、能量守恒和高阶矩的关系所确定的待定系数 [46] ,即
是由质量守恒、动量守恒、能量守恒和高阶矩的关系所确定的待定系数 [46] ,即
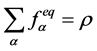 , (5)
, (5)
 , (6)
, (6)
 , (7)
, (7)
 , (8)
, (8)
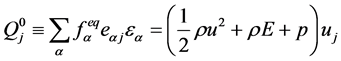 , (9)
, (9)
 , (10)
, (10)
 . (11)
. (11)
其中 为理想气体的压力
为理想气体的压力
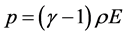 , (12)
, (12)
 为比热比。
为比热比。
2.2. 平衡态分布中的系数
Navier-Stokes方程的恢复与矩的对称性有关
 . (13)
. (13)
本文中的六个矩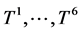 可由文献 [57] 得出
可由文献 [57] 得出
 , (14)
, (14)
 , (15)
, (15)
其中, 。
。
 , (16)
, (16)
 (17)
(17)
所以
 (18)
(18)
将平衡态分布函数带入(5)~(11)式,再使用(14)~(18)式,即可以得到关于系数 ,
, ,
, ,
,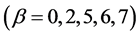
 ,
,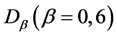 的线性方程组
的线性方程组
 , (19)
, (19)
 , (20)
, (20)
 , (21)
, (21)
 , (22)
, (22)
 , (23)
, (23)
 (24)
(24)
 ,(25)
,(25)
 , (26)
, (26)
 , (27)
, (27)
 , (28)
, (28)
 , (29)
, (29)
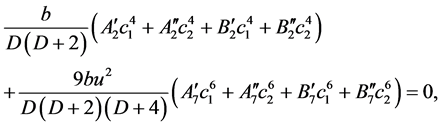 (30)
(30)
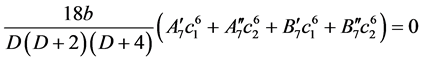 , (31)
, (31)
 , (32)
, (32)
 , (33)
, (33)
 (34)
(34)
其中, 是空间维度,
是空间维度, (
( ,正六边形格子) 是每个位置的节点数。
,正六边形格子) 是每个位置的节点数。
为了得到平衡态分布函数中的系数,根据气体静止时的各向同性,我们提出了一些补充条件。如引入下列假设
 , (35)
, (35)
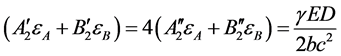 , (36)
, (36)
 , (37)
, (37)
 , (38)
, (38)
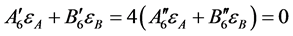 , (39)
, (39)
 , (40)
, (40)
得到系数
 , (41)
, (41)
 , (42)
, (42)
 , (43)
, (43)
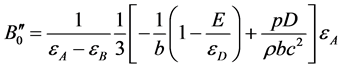 , (44)
, (44)
 , (45)
, (45)
 , (46)
, (46)
 , (47)
, (47)
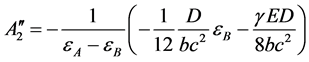 , (48)
, (48)
 , (49)
, (49)
 , (50)
, (50)
 , (51)
, (51)
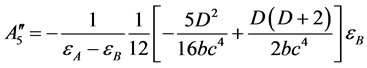 , (52)
, (52)
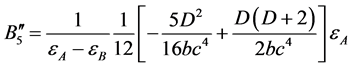 , (53)
, (53)
 , (54)
, (54)
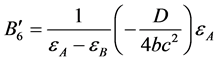 , (55)
, (55)
 , (56)
, (56)
 , (57)
, (57)
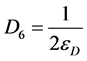 , (58)
, (58)
 , (59)
, (59)
 , (60)
, (60)
 , (61)
, (61)
 . (62)
. (62)
2.3. 宏观方程
假设Knudsen数 为小量,对分布函数
为小量,对分布函数 进行Chapman- Enskog展开 [58]
进行Chapman- Enskog展开 [58]
 , (63)
, (63)
在(63)式中, 表示
表示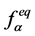 。
。
引入 等空间尺度,
等空间尺度, ,即
,即
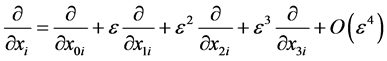 . (64)
. (64)
对(4)式进行Taylor展开,保留到 ,可得到不同空间尺度的一系列偏微分方程组,即
,可得到不同空间尺度的一系列偏微分方程组,即
 , (65)
, (65)
 , (66)
, (66)
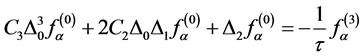 , (67)
, (67)
 . (68)
. (68)
其中, ,
,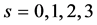 。(65)~(68)式被称为不同空间尺度的系列方程,可用于一维、二维、三维等情况。(11)~(16)式中关于松弛因子
。(65)~(68)式被称为不同空间尺度的系列方程,可用于一维、二维、三维等情况。(11)~(16)式中关于松弛因子 的多项式为
的多项式为
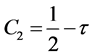 , (69)
, (69)
 , (70)
, (70)
 . (71)
. (71)
公式(69)~(71)称为Chapman多项式,与文献 [59] 所得到的结果完全一致。它们可用来表示修正的偏微分方程的扩散项和色散项系数。
我们很容易得到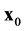 尺度的守恒率方程
尺度的守恒率方程
 , (72)
, (72)
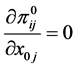 , (73)
, (73)
 . (74)
. (74)
将(65) + (66) 两端分别乘以1,
两端分别乘以1, 和
和 ,并分别对
,并分别对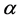 求和,即可得到具有二阶精度的定常Euler方程
求和,即可得到具有二阶精度的定常Euler方程
 , (75)
, (75)
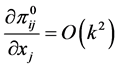 , (76)
, (76)
 . (77)
. (77)
3. 数值例子
3.1. 4Mach数圆柱绕流 [46]
把求解域 分成
分成 的均匀网格。圆柱横截面的半径为
的均匀网格。圆柱横截面的半径为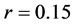 ,圆心坐标为
,圆心坐标为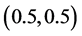 。
。
迭代的初始条件为 ,
, ,
, ,
,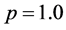 ,即入流Mach数为
,即入流Mach数为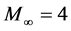 ,
, 。入口边界、上边界和下边界的边界条件与初始条件相同;出口边界条件为Neumann条件,即
。入口边界、上边界和下边界的边界条件与初始条件相同;出口边界条件为Neumann条件,即 ,其中
,其中 为
为 、
、 、
、 或
或 ;
;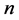 为法线方向的矢量。圆柱表面为粘性边界条件,即
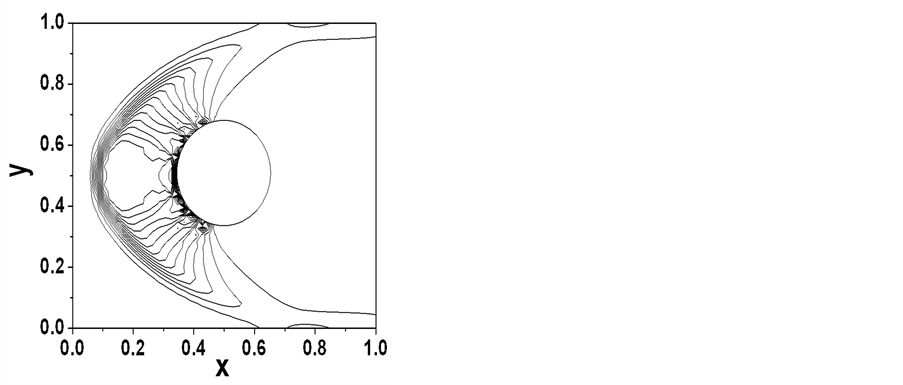
为法线方向的矢量。圆柱表面为粘性边界条件,即 。图2给出了Mach数为4时圆柱绕流的模拟结果,其中(a)为密度等值线图,(b)为压力等值线图,
。图2给出了Mach数为4时圆柱绕流的模拟结果,其中(a)为密度等值线图,(b)为压力等值线图, 、
、 轴为流场计算区域的坐标。我们在等值线中发现了一些大梯度区振荡,这是由边界区域的精度较低导致的,因为我们使用了矩形网格构建圆柱边界。由于流体是超音速流,因此边界的处理对激波没有影响。为了与以前LBM模型所得的结果作比较,我们选择了文献 [41] 中的一阶LBM模型和文献 [46] 中的二阶LBM模型,并把文献 [60] 中有限谱ENO模型(FSEM)所得的结果作为解析解。表1给出了
轴为流场计算区域的坐标。我们在等值线中发现了一些大梯度区振荡,这是由边界区域的精度较低导致的,因为我们使用了矩形网格构建圆柱边界。由于流体是超音速流,因此边界的处理对激波没有影响。为了与以前LBM模型所得的结果作比较,我们选择了文献 [41] 中的一阶LBM模型和文献 [46] 中的二阶LBM模型,并把文献 [60] 中有限谱ENO模型(FSEM)所得的结果作为解析解。表1给出了 时本文所使用的LBM模型与其它模型的
时本文所使用的LBM模型与其它模型的 范数误差。从表1中可以发现,本模型的精度较文献 [41] 和文献 [46] 略有提高。
范数误差。从表1中可以发现,本模型的精度较文献 [41] 和文献 [46] 略有提高。

 (a) (b)
(a) (b)
Figure 2. Numerical result of 4 Mach number incoming flow around a circular cylinder. (a) is the density contours, (b) is the pressure contours
图2. 4 Mach数圆柱绕流模拟结果。(a) 密度等值线图,(b) 压力等值线图
Table 1. The L1 norm errors of the flows around a circular cylinder with 4 Mach number incoming at line x = 0.25
表1. x = 0.25时,4 Mach数圆柱绕流的L1范数误差

 (a) (b)
(a) (b)
Figure 3. Numerical result of 3 Mach number incoming flow around a rectangle. (a) is the density contours, (b) is the pressure contours
图3. 3 Ma数前台阶流模拟结果。(a) 密度等值线图,(b) 压力等值线图
3.2. 3Mach数前台阶流
把求解域 分成
分成 的均匀网格。矩形位于
的均匀网格。矩形位于 。迭代的初始条件
。迭代的初始条件
为 ,
, ,
, ,
,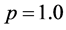 ,即入流Mach数为
,即入流Mach数为 ,
,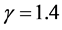 。边界条件与图2相同。图3给出了入流Mach数为3时,绕前台阶流动的数值模拟结果。其中图3(a)为密度等值线图,图3(b)为压力等值线图。其它参数为
。边界条件与图2相同。图3给出了入流Mach数为3时,绕前台阶流动的数值模拟结果。其中图3(a)为密度等值线图,图3(b)为压力等值线图。其它参数为 ,
,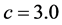 ,
, ,
,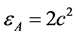 ,
, ,
, ,网格数为
,网格数为 ,Mach数为3,等值线条数为30。数值结果表明,LBM模型所得到的结果与经典结果吻合的较好。
,Mach数为3,等值线条数为30。数值结果表明,LBM模型所得到的结果与经典结果吻合的较好。
4. 结论
本文提出了用于定常可压缩流动的多能级格子Boltzmann模型,并得出以下结论:
首先,给出了定常格子Boltzmann方程,得到了不同空间尺度的一系列偏微分方程。使用了Chapman-Enskog展开和空间多尺度展开描述平衡态分布函数的高阶矩。
其次,得到了具有高阶截断误差的Euler方程的修正方程。
本文仍有后续问题需要解决:(1) 模型精度问题。本模型中的数值耗散和色散,以及数值现象与参数之间的关系仍需要研究;(2) 固定边界的边界条件及更高Mach数的流动仍需更细致地模拟。这些问题将在以后的文章中讨论。
最后,我们需要指出,建立用于模拟可压缩流动乃至高Mach数流动的格子Boltzmann模型仍是需要解决的问题。
基金项目
国家自然科学基金(NO.51406067,NO.11272133),吉林省教育厅科研项目(吉教科合字[2016]第141号)资助。
文章引用
闫铂,王建朝,闫广武. 一种定常可压缩流动的格子Boltzmann模型
A Lattice Boltzmann Model for the Steady State Compressible Flows[J]. 流体动力学, 2017, 05(01): 10-21. http://dx.doi.org/10.12677/IJFD.2017.51002
参考文献 (References)
- 1. Chen, H.D., Chen, S.Y. and Matthaeus, M.H. (1992) Recovery of the Navier-Stokes Equations Using a Lattice Boltzmann Gas Method. Physical Review A, 45, 5339-5342. https://doi.org/10.1103/PhysRevA.45.R5339
- 2. Koelman, J.M.V.A. (1991) A Simple Lattice Boltzmann Scheme for Navier-Stokes Fluid Flow. Europhysics Letters, 15, 603-607. https://doi.org/10.1209/0295-5075/15/6/007
- 3. Benzi, R., Succi, S. and Vergassola, M. (1992) The Lattice Boltzmann Equations: Theory and Applications. Physics Reports, 222, 147-197. https://doi.org/10.1016/0370-1573(92)90090-m
- 4. Chen, S.Y. and Doolen, G.D. (1998) Lattice Boltzmann Method for Fluid Flows. Annual Review of Fluid Mechanics, 30, 329-364. https://doi.org/10.1146/annurev.fluid.30.1.329
- 5. Shan, X.W. and Chen, H.D. (1994) Simulation of Non-Ideal Gases Liquid Gas Phase Transitions by the Lattice Boltzmann Equation. Physical Review E, 49, 2941. https://doi.org/10.1103/PhysRevE.49.2941
- 6. Filippova, O. and Hanel, D. (1997) Lattice Boltzmann Simulation of Gas Particle Flow in Filters. Computer & Fluids, 26, 697-712. https://doi.org/10.1016/S0045-7930(97)00009-1
- 7. Succi, S., Foti, E. and Higuera, F.J. (1989) 3-Dimensional Flows in Complex Geometries with the Lattice Boltzmann Method. Europhysics Letters, 10, 433. https://doi.org/10.1209/0295-5075/10/5/008
- 8. Ladd, A. (1994) Numerical Simulations of Particle Suspensions via a Discretized Boltzmann Equation. Part 2. Numerical Results. Journal of Fluid Mechanics, 271, 311. https://doi.org/10.1017/S0022112094001783
- 9. Velivelli, A.C. and Bryden, K.M. (2006) Parallel Performance and Accuracy of Lattice Boltzmann and Traditional Finite Difference Methods for Solving the Unsteady Two Dimensional Burger’s Equation. Physica A, 362, 139-145. https://doi.org/10.1016/j.physa.2005.09.031
- 10. Zhang, J.Y. and Yan, G.W. (2008) Lattice Boltzmann Methods for One and Two-Dimensional Burger’s Equation. Physica A: Statistical Mechanics and its Applications, 387, 4771-4786.
- 11. Yan, G.W. and Zhang, J.Y. (2009) A Higher-Order Moment Method of the Lattice Boltzmann Model for the Korteweg-Devries Equation. Mathematics and Computers in Simulation, 79, 1554-1565. https://doi.org/10.1016/j.matcom.2008.07.006
- 12. Yan, G.W. and Yuan, L. (2001) Lattice Bhatnagar-Gross-Krook Model for the Lorenz Attractor. Physica D, 154, 43-50. https://doi.org/10.1016/S0167-2789(01)00224-X
- 13. Succi, S. (1993) Lattice Boltzmann Equation for Quantum Mechanics. Physica D, 69, 327-332. https://doi.org/10.1016/0167-2789(93)90096-J
- 14. Palpacelli, S. and Succi, S. (2007) Numerical Validation of the Quantum Lattice Boltzmann Scheme in Two and Three Dimension. Physical Review E, 75, Article ID: 066704. https://doi.org/10.1103/PhysRevE.75.066704
- 15. Zhong, L.H., Feng, S.D., Dong, P. and Gao, S.T. (2006) Lattice Boltzmann Schemes for the Nonlinear Schrodinger Equation. Physical Review E, 74, Article ID: 036704. https://doi.org/10.1103/PhysRevE.74.036704
- 16. Chai, Z.H. and Shi, B.C. (2007) A Novel Lattice Boltzmann Model for the Poisson Equation. Applied Mathematical Modelling, 32, 2050-2058.
- 17. Wang, M.R., Wang, J.K. and Chen, S.Y. (2007) Roughness and Cavitations Effect on Electro-Osmotic Flows in Rough Microchannels Using the Lattice Poisson-Boltzmann Methods. Journal of Computational Physics, 226, 836-851.
- 18. Alexander, F.J., Chen, H., Chen, S., et al. (1992) Lattice Boltzmann Model for Compressible Fluids. Physical Review A, 46, 1967-1970. https://doi.org/10.1103/PhysRevA.46.1967
- 19. Yu, H.D. and Zhao, K.H. (2000) Lattice Boltzmann Method for Compressible Flows with High Mach Number. Physical Review E, 61, 3867-3870. https://doi.org/10.1103/PhysRevE.61.3867
- 20. Prasiankis, N.I. and Boulouchos, K.B. (2007) Lattice Boltzmann Method for Simulation of Weakly Compressible Flows at Arbitrary Prandtl Number. International Journal of Modern Physics C, 18, 602-609. https://doi.org/10.1142/S012918310701084X
- 21. Nadiga, B.T. (1995) An Euler Solver Based on Locally Adaptive Discrete Velocities. Journal of Statistical Physics, 81, 129-146. https://doi.org/10.1007/BF02179972
- 22. Prendergast, K.H. and Xu, K. (1993) Numerical Hydrodynamics from Gas-Kinetic Theory. Journal of Computational Physics, 109, 53-66. https://doi.org/10.1006/jcph.1993.1198
- 23. Kim, C., Xu, K., Martinelli, L., et al. (1997) Analysis and Implementation of the Gas Kinetic BGK Scheme for Computing Inhomogeneous Fluid Behavior. International Journal for Numerical Methods in Fluids, 25, 21-49. https://doi.org/10.1002/(SICI)1097-0363(19970715)25:1<21::AID-FLD515>3.0.CO;2-Y
- 24. Kotelnikov, A.D. and Montgomery, D.C. (1997) A Kinetic Method for Computing Inhomogeneous Fluid Behavior. Journal of Computational Physics, 134, 364-388. https://doi.org/10.1006/jcph.1997.5720
- 25. Huang, J., Xu, F., Vallieres, M., et al. (1997) A Thermal LBGK Model for Large Density and Temperature Difference. International Journal of Modern Physics C, 8, 827-841.
- 26. Renda, A., Bella, G., Succi, S., et al. (1998) Thermo Dydrodynamics Lattice BGK Schemes with Non-Perturbative Equilibrium. Europhysics Letters, 41, 279-283. https://doi.org/10.1209/epl/i1998-00143-x
- 27. Vahala, G., Pavlo, P., Vahala, L., et al. (1998) Thermal Lattice Boltzmann Models (TLBM) for Compressible Flows. International Journal of Modern Physics C, 9, 1247-1261.
- 28. De Cicco, M., Succi, S. and Bella, G. (1999) Nonlinear Stability of Compressible Thermal Lattice BGK Model. SIAM Journal on Scientific Computing, 21, 366-377. https://doi.org/10.1137/S1064827597319805
- 29. Palmer, B.J. and Rector, D.R. (2000) Lattice Boltzmann Algorithm for Simulating Thermal Flow in Compressible Fluids. Journal of Computational Physics, 161, 1-20. https://doi.org/10.1006/jcph.2000.6425
- 30. Qu, K., Shu, Q. and Chew, Y.T. (2007) Alternative Method to Construct Equilibrium Distribution Function in Lattice Boltzmann Method Simulation of Inviscid Compressible Flows at High Mach Number. Physical Review E, 75, Article ID: 036706. https://doi.org/10.1103/PhysRevE.75.036706
- 31. Hinton, F.L., Rosenbluth, M.N., Wong, S.K., Lin-Liu, Y.R. and Miller, R.L. (2001) Modified Lattice Boltzmann Method for Compressible Fluid Simulation. Physical Review E, 63, Article ID: 061212. https://doi.org/10.1103/PhysRevE.63.061212
- 32. Gan, Y.B., Xu, A.G., Zhang, G.C., Yu, X.J. and Li, Y.J. (2008) Two-Dimensional Lattice Boltzmann Model for Compressible Flows with High Mach Number. Physica A, 387, 1721-1732. https://doi.org/10.1016/j.physa.2007.11.013
- 33. Ancona, M.G. (1994) Fully-Lagrangian and Lattice Boltzmann Methods for Solving Systems of Conservation Equations. Journal of Computational Physics, 115, 107-120. https://doi.org/10.1006/jcph.1994.1181
- 34. Pan, X.P., Xu, A.G., Zhang, G.C. and Jiang, S. (2007) Lattice Boltzmann Approach to High-Speed Compressible Flows. International Journal of Modern Physics C, 18, 1747-1764. https://doi.org/10.1142/S0129183107011716
- 35. Wang, Y., He, Y.L., Zhao, T.S., Tang, G.H. and Tao, W.Q. (2007) Implicit-Explicit Finite-Difference Lattice Boltzmann Method for Compressible Flows. International Journal of Modern Physics C, 18, 1961-1983. https://doi.org/10.1142/S0129183107011868
- 36. Tsutahara, M., Kataoka, T., Shikata, K. and Takada, N. (2008) New Model and Scheme for Compressible Fluids of the Finite Difference Lattice Boltzmann Method and Direct Dimulations of Aerodynamics Sound. Computers & Fluids, 37, 79-89. https://doi.org/10.1016/j.compfluid.2005.12.002
- 37. Brownlee, R., Gorban, A.N. and Levesly, J. (2007) Stable Simulation of Fluid Flow with High-Reynolds Number Using Ehrenfests’ Steps. Numerical Algorithms, 45, 389-408. https://doi.org/10.1007/s11075-007-9087-1
- 38. Li, Q., He, Y.L., Wang, Y. and Tao, W.Q. (2007) Coupled Double-Distribution-Function Lattice Boltzmann Method for the Compressible Navier-Stokes Equation. Physical Review E, 76, Article ID: 056705. https://doi.org/10.1103/PhysRevE.76.056705
- 39. Sun, C.H. (1998) Lattice Boltzmann Model for High Speed Flows. Physical Review E, 58, 7283-7287. https://doi.org/10.1103/PhysRevE.58.7283
- 40. Junk, M. (1999) Kinetic Schemes in the Case of Low Mach Numbers. Journal of Computational Physics, 151, 947- 968. https://doi.org/10.1006/jcph.1999.6228
- 41. Yan, G.W., Chen, Y.S. and Hu, S.X. (1999) Simple Lattice Boltzmann Model for Simulating Flows with Shock Wave. Physical Review E, 59, 454-459. https://doi.org/10.1103/PhysRevE.59.454
- 42. Mason, R.J. (2000) A Compressible Lattice Boltzmann Model. Bulletin of the American Physical Society, 45, 168-170.
- 43. Mason, R.J. (2002) A Multi-Speed Compressible Lattice Boltzmann Model. Journal of Statistical Physics, 107, 385- 400. https://doi.org/10.1023/A:1014535310153
- 44. Kataoka, T. and Tsutahara, M. (2004) Lattice Boltzmann Method for the Compressible Euler Equations. Physical Review E, 69, Article ID: 056702. https://doi.org/10.1103/PhysRevE.69.056702
- 45. Kataoka, T. and Tsutahara, M. (2004) Lattice Boltzmann Method for the Compressible Navier-Stokes Equations with Flexible Specific-Heat Ratio. Physical Review E, 69, Article ID: 035701. https://doi.org/10.1103/PhysRevE.69.035701
- 46. Yan, G.W., Zhang, J.Y., Liu, Y.H. and Dong, Y.F. (2007) A Multi-Energy-Level Lattice Boltzmann Model for the Compressible Navier-Stokes Equations. International Journal for Numerical Methods in Fluids, 55, 41-56.
- 47. Yan, G.W. and Yuan, L. (2000) Lattice Boltzmann Model for the Perfect Gas Flows with Near Vacuum Region. Communication in Nonlinear Science and Numerical Simulation, 5, 58-63. https://doi.org/10.1016/S1007-5704(00)90002-9
- 48. Zhang, J.Y., Yan, G.W., Shi, X.B. and Dong, Y.F. (2009) A Lattice Boltzmann Model for the Compressible Euler Equations with Second-Order Accuracy. International Journal for Numerical Methods in Fluids, 60, 95-117. https://doi.org/10.1002/fld.1883
- 49. Yan, G.W. and Zhang, J.Y. (2008) A Multi-Entropy-Level Lattice Boltzmann Model for the One Dimensional Compressible Euler Equations. International Journal of Computational Fluid Dynamics, 22, 383-392. https://doi.org/10.1080/10618560802119673
- 50. Versteeg, H.K. and Malalasekera, W. (1995) An Introduction to Computational Fluid Dynamics. The Finite Volume Method, Longman Group Ltd., London, 1-257.
- 51. Harten, A. (1984) On a Class of High Resolution Total Variation Stable Finite Difference Schemes. SIAM Journal on Numerical Analysis, 21, 1-23. https://doi.org/10.1137/0721001
- 52. Harten, A., Engquist, B., Osher, S. and Chakravathy, R. (1997) Uniformly High Order Accurate Essentially Non-Os- cilltory Schemes, III. Journal of Computational Physics, 131, 3-47. https://doi.org/10.1006/jcph.1996.5632
- 53. Zhang, L.T., Wagner, G.J. and Liu, W.K. (2002) A Parallelized Meshfree Method with Boundary Enrichment for Large-Scale CFD. Journal of Computational Physics, 176, 483-506. https://doi.org/10.1006/jcph.2002.6999
- 54. Sethian, J.A. (1995) Theory, Algorithms and Applications of Level Set Methods for Propagating Interface. Acta Numerica, Cambridge University Press, Cambridge, 309-395.
- 55. Bernashi, M., Succi, S. and Chen, H. (2001) Accelerated Lattice Schemes for Steady-State Flows Simulations. Journal of Scientific Computing, 16, 135-144. https://doi.org/10.1023/A:1012230722915
- 56. Guo, Z.L., Zhao, T.S. and Shi, Y. (2004) Preconditioned Lattice Boltzmann Method for Steady Flows. Physical Review E, 70, Article ID: 066706. https://doi.org/10.1103/PhysRevE.70.066706
- 57. Wolfram, S. (1986) Cellular Automaton Fluids 1: Basic Theory. Journal of Statistical Physics, 45, 471-518. https://doi.org/10.1007/BF01021083
- 58. Chapman, S. and Cowling, T.G. (1970) The Mathematical Theory of Non-Uniform Gas. Cambridge University Press, Cambridge, 389-575.
- 59. Holdych, D.J., Noble, D.R., Georgiadis, J.G., et al. (2004) Truncation Error Analysis of Lattice Boltzmann Methods. Journal of Computational Physics, 193, 595-619. https://doi.org/10.1016/j.jcp.2003.08.012
- 60. Wang, J.P., Qiu, Q.H. and Ogawa, S. (2004) Numerical Simulation of Viscous Supersonic Flows by Finite Spectral ENO Method. Computational Fluid Dynamics Journal, 12, 191-197.
