Pure Mathematics
Vol.05 No.06(2015), Article ID:16295,4 pages
10.12677/PM.2015.56036
Study on the Solvability of Matrix Equation
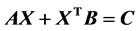
Linlin Zhao, Jinchan Wang
Department of Mathematics, Dezhou University, Dezhou Shandong
Received: Oct. 16th, 2015; accepted: Nov. 2nd, 2015; published: Nov. 6th, 2015
Copyright © 2015 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
The problem of the solvability for the matrix equation
 is studied by using the matrix decomposition and its Moore-Penrose generalized inverse.
Some solvability conditions are obtained and the general expression of its solution
is given.
is studied by using the matrix decomposition and its Moore-Penrose generalized inverse.
Some solvability conditions are obtained and the general expression of its solution
is given.
Keywords:Matrix Equation, Solvability, Generalized Inverse

矩阵方程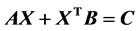 的解
的解
赵琳琳,王金婵
德州学院数学科学学院,山东 德州

收稿日期:2015年10月16日;录用日期:2015年11月2日;发布日期:2015年11月6日

摘 要
利用矩阵分解,结合矩阵广义逆理论,研究了矩阵方程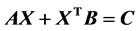 有解的条件,得到了方程有解时解的一般表达式。
有解的条件,得到了方程有解时解的一般表达式。
关键词 :矩阵方程,可解性,广义逆

1. 引言
令 表示所有
表示所有 复矩阵的集合。符号
复矩阵的集合。符号 ,
,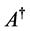 ,
,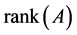 分别表示矩阵
分别表示矩阵 的转置,Moore-Penrose逆和秩。矩阵方程
的转置,Moore-Penrose逆和秩。矩阵方程 在观察器设计、带有输入约束的控制系统和故障检验等领域中有着广泛的应用。对于上述方程,文献[1]
利用矩阵的广义逆给出了C为复对称矩阵时它可解的条件;文献[2] 利用正则矩阵束得到了它唯一可解的条件;文献[3] 研究了方程
在观察器设计、带有输入约束的控制系统和故障检验等领域中有着广泛的应用。对于上述方程,文献[1]
利用矩阵的广义逆给出了C为复对称矩阵时它可解的条件;文献[2] 利用正则矩阵束得到了它唯一可解的条件;文献[3] 研究了方程 的一般解;文献[4] 讨论了算子方程
的一般解;文献[4] 讨论了算子方程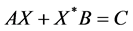 的可解性质。本文将利用矩阵分解及其广义逆讨论矩阵方程
的可解性质。本文将利用矩阵分解及其广义逆讨论矩阵方程 的一般可解性及解的表达式。
的一般可解性及解的表达式。
2. 主要结果
本文以下所有讨论中符号 表示适当阶数的单位矩阵,下面我们首先给出两个引理。
表示适当阶数的单位矩阵,下面我们首先给出两个引理。
引理2.1 [5] :设 。则方程
。则方程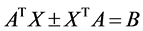 有解当且仅当
有解当且仅当
 ,
,
且其一般解可表示为

其中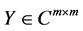 为任意矩阵,
为任意矩阵,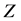 满足
满足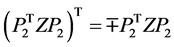 ,这里
,这里 。
。
引理2.2 [6] :设 ,
, 。则方程
。则方程 有解当且仅当
有解当且仅当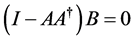 ,且其一般解可表示为
,且其一般解可表示为 ,其中
,其中 为任意矩阵。
为任意矩阵。
定理2.1:设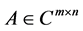 ,
,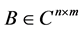 ,
,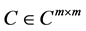 。令
。令 。若
。若 是行满秩的,则方程
是行满秩的,则方程 可解,并且
可解,并且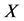 可表示为
可表示为
 (1)
(1)
其中 为任意矩阵并满足
为任意矩阵并满足 ,
,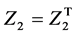 ,
,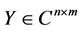 为任意矩阵。
为任意矩阵。
证明:方程 等价于
等价于

由方程 和上述方程可得,
和上述方程可得,
 (2)
(2)
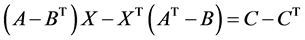 (3)
(3)
方程 有解等价于方程(2)和(3)有公共解。由引理2.1可得,
有解等价于方程(2)和(3)有公共解。由引理2.1可得,
 ,其中
,其中
 ,其中
,其中
由以上两方程得,
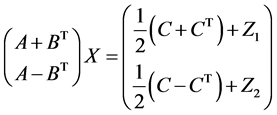
由引理2.2,若 是行满秩的,则方程
是行满秩的,则方程 可解,并且
可解,并且 可由(1)式表示。
可由(1)式表示。
定理2.2:设 ,
, ,
,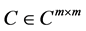 。若
。若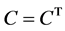 ,则方程
,则方程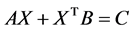 可解的充要条件是存在矩阵
可解的充要条件是存在矩阵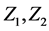 满足
满足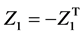 ,
, 使得
使得
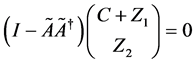
且它的一般解可表示为

其中 ,
, 为任意矩阵。
为任意矩阵。
证明:由定理2.1和引理2.2易证。
在实践中经常会遇到定束,定义为:若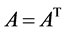 ,
, 且
且 为正定矩阵,则称
为正定矩阵,则称 为定束。对于
为定束。对于 阶矩阵
阶矩阵 满足
满足 ,
, ,由文献([6]
, p. 152)可知存在非奇异实矩阵
,由文献([6]
, p. 152)可知存在非奇异实矩阵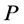 使得
使得
 (4)
(4)
 (5)
(5)
由上述性质可得方程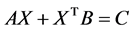 可解的另一条件。
可解的另一条件。
定理2.3:设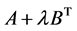 为定束,其中
为定束,其中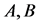 均为
均为 阶矩阵,则方程
阶矩阵,则方程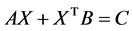 可解当且仅当
可解当且仅当
 且
且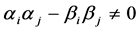 ,
, (6)
(6)
若令 ,则其一般解可表示为
,则其一般解可表示为
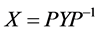 (7)
(7)
这里 ,
,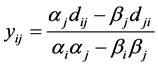 ,
,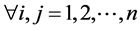 。
。
证明:由(4)和(5)式可得,方程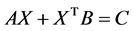 等价于
等价于

令 ,
, 。则
。则
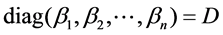

上面的方程可分解为如下的 个方程
个方程

和如下的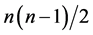 个二阶系统
个二阶系统
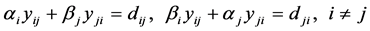
由上面的方程可得当(6)式成立时,方程有解且解可由(7)式表示。
3. 结论
通过矩阵分解及其广义逆,研究了矩阵方程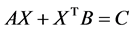 的可解性,得到了若干可解的条件和解的一般表达式。
的可解性,得到了若干可解的条件和解的一般表达式。
基金项目
山东省高等学校科研发展计划项目(J13LI53)。
文章引用
赵琳琳,王金婵. 矩阵方程AX+XTB=C的解
Study on the Solvability of Matrix Equation AX+XTB=C[J].
理论数学, 2015, 05(06): 255-258. http://dx.doi.org/10.12677/PM.2015.56036
参考文献 (References)
- 1. Piao, F.X., Zhang, Q.L. and Wang, Z.F. (2007) The Solution to Matrix Equation . Journal of the Franklin Institute, 344, 1056-1062. http://dx.doi.org/10.1016/j.jfranklin.2007.05.002
- 2. Ikramov, K. (2010) Conditions for Unique Solvability of the Matrix Equation . Doklady Mathematics, 81, 63-65. http://dx.doi.org/10.1134/S1064562410010187
- 3. Teran, F. and Dopico, F. (2011) The Solution of the Equation and Its Applications to the Theory of Orbits. Linear Algebra and Its Applications, 434, 44-67. http://dx.doi.org/10.1016/j.laa.2010.08.005
- 4. Braden, H. (1998) The Equation . SIAM Journal on Matrix Analysis and Applications, 20, 295-302. http://dx.doi.org/10.1137/S0895479897323270
- 5. Ben-Israel, A. and Greville, T.N.E. (2003) Generelized In-verse Theory and Applications. 2nd Edition, Springer, Berlin.
- 6. 赵琳琳. 算子方程 的解[J]. 纯粹数学与应用数学, 2012, 28(4): 469-474.