长安大学，理学院，陕西 西安

收稿日期：2021年4月1日；录用日期：2021年4月30日；发布日期：2021年5月8日

摘要

一个图的邻接矩阵的特征值称为图的特征值，图的所有特征值的多重集称为图的谱。如果图的一个特征值所对应的特征空间与全1向量不正交，则称其为主特征值，主特征值对于刻画图及研究图的性质都有重要的意义。刻画恰有 $k\left(2\le k\le n\right)$ 个主特征值的图是一个存在已久的问题，本文给出了一类树的主特征值数目的下界。

关键词

邻接矩阵，主特征值，树图

Characterization of the Number of Main Eigenvalues of a Class of Trees

Zenan Du, Qian Yu

School of Science, Chang’an University, Xi’an Shaanxi

Received: Apr. 1^st, 2021; accepted: Apr. 30^th, 2021; published: May 8^th, 2021

ABSTRACT

The eigenvalues of the adjacency matrix of a graph are called the eigenvalues of a graph, the multi-set of all eigenvalues of a graph is called the spectrum of a graph. An eigenvalue of a graph is a main eigenvalue if its eigenspace is not orthogonal to the all-ones vector, the main eigenvalues are significant to the characterization of graphs and the properties of graphs. Characterizing graphs with $k\left(2\le k\le n\right)$ number of main eigenvalues are a long-standing problem. In this paper, the lower bound of main eigenvalues of a class of trees is determined.

Keywords:Adjacency Matrix, Main Eigenvalues, Tree

Copyright © 2021 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

图论起源于18世纪哥尼斯堡七桥问题，瑞士数学家Leonhard Euler在1736年发表了一篇解决七桥问题的论文，该论文被认为是图论的第一篇论文，Euler因此也被誉为图论之父。1936年匈牙利数学家König出版了第一本图论专著《Theory of Directed and Undirected Graphs》，标志着图论正式成为一门独立的学科。作为离散数学重要的分支之一，图论已发展成一门独立的学科，它主要研究某一集合元素间可用拓扑图形表示的二元关系。根据研究方法和内容的不同，图论已衍生出许多分支，如拓扑图论、代数图论、随机图论、结构图论、模糊图论、极值图论、超图论等。图谱理论作为代数图论中的一个重要分支，与群论、矩阵论、组合数学、多项式理论、线性代数等学科都有着密切的联系，它主要研究图的组合性质和图相关矩阵(如邻接矩阵，拉普拉斯矩阵，无符号拉普拉斯矩阵，距离矩阵)的代数性质之间的关系。

一个图的邻接矩阵的特征值称为图的特征值，图的所有特征值的多重集称为图的谱。1978年Cvetković D. [1] 第一次提出了图的主特征值的概念。若图的邻接矩阵A的特征值 $\lambda$ 存在一个特征向量x，满足x与元素全为1的向量e不正交，即 $e^{\text{T}}x\ne 0$，那么就称 $\lambda$ 为图的一个主特征值。Cvetković D.在文献 [1] 中提出问题，如何刻画恰有 $k\left(2\le k\le n\right)$ 个主特征值的图。对于一个连通图G，因为其邻接矩阵是不可约的，故由著名的Perron-Frobenius定理可知G的最大特征值为主特征值。更一般的，恰有一个主特征值的图为正则图 [1]。已经有一系列论文对于恰有两个主特征值的图进行了刻画，如Cardoso [2]，Hagos [3]， Hayat [4]，Hou et al. [5] [6] [7]，Lepović [8]，Shi [9] 等，然而这项工作还远未完成。2012年Godsil C. [10] 猜想：几乎所有图的全部特征值均为主特征值，2016年O’Rourke [11] 证明了这个猜想的正确性，该结论说明主特征值对于刻画图及研究图的性质都有重要的意义。

2. 预备知识

定义2.1 [12] 对于n个顶点的图，其邻接矩阵定义为 $A={\left(a_{ij}\right)}_{n\times n}$，其中 $a_{ij}=\{\begin{array}{l}1,若v_i和v_j相邻\\ 0，其它\end{array}$。

由上述定义可知邻接矩阵为实对称矩阵且主对角元素为0。

定义2.2 [12] 路图 $P_n$ 表示从一个顶点 $v_1$ 出发，依次将新点 $v_i$ 与 $v_{i-1}$ $\left(i\le n\right)$ 相连所得到的图。

定理2.3 [13] 路图 $P_n$ 的特征多项式为 ${\phi }_0\left(x\right)=1$，${\phi }_1\left(x\right)=x$，${\phi }_n(x)=x{\phi }_{n-1}\left(x\right)-{\phi }_{n-2}\left(x\right)$ $\left(n\ge 2\right)$。

推论2.4 当 $n=2k$ 时， ${\phi }_n\left(x\right)$ 为偶函数；当 $n=2k+1$ 时， ${\phi }_n\left(x\right)$ 为奇函数。

证明： $k=0$ 时结论显然成立，

$k=1$ 时， ${\phi }_2\left(-x\right)=-x{\phi }_1\left(-x\right)-{\phi }_0\left(-x\right)=x{\phi }_1\left(x\right)-{\phi }_0\left(x\right)={\phi }_2\left(x\right)$，

${\phi }_3\left(-x\right)=-x{\phi }_2\left(-x\right)-{\phi }_1\left(-x\right)=-x{\phi }_2\left(x\right)+{\phi }_1\left(x\right)=-{\phi }_3\left(x\right)$，成立。

$k=2$ 时， ${\phi }_4\left(-x\right)=-x{\phi }_3\left(-x\right)-{\phi }_2\left(-x\right)=x{\phi }_3\left(x\right)-{\phi }_2\left(x\right)={\phi }_4\left(x\right)$，

${\phi }_5\left(-x\right)=-x{\phi }_4\left(-x\right)-{\phi }_3\left(-x\right)=-x{\phi }_4\left(x\right)+{\phi }_3\left(x\right)=-{\phi }_5\left(x\right)$，成立。

以此类推，n为奇偶的情况可交替证明，故结论成立。

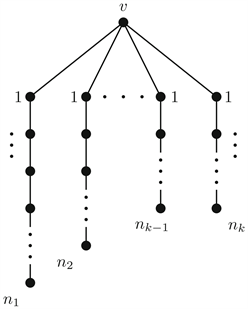
定义2.5 [14] 星形树 $S\left(n_1,n_2,n_3,\cdots ,n_k\right)$ 表示将一个顶点 $v$ 分别与路 $P_{n_1},\cdots ,P_{n_k}$ 的一端相连所构成的图，见图1。

图1. $S\left(n_1,n_2,n_3,\cdots ,n_k\right)$

定理2.6 [14] 对于正整数m，星形树 $S\left(1,1,m\right)$ 的特征值为：

$Spec\left(S\left(1,1,m\right)\right)=\left\{2\cos \left(\frac{2k+1}{2m+4}\pi \right):k=0,1,\cdots ,m+1\right\}\cup \left\{0\right\}$

定义2.7 [12] 若图G的顶点集可划分为两个非空子集X和Y，使得图G的任一条边都有一个端点在X中，另一个端点在Y中，则称图G为二部图。

推论2.8 [12] 若图G为二部图，顶点集可划分为X和Y，其中它们的阶数分别s和t，则其全部特征值关于原点对称。进一步若特征值 $\lambda$ 对应特征向量 $x={\left(x_1,\cdots ,x_s,y_1,\cdots ,y_t\right)}^{\text{T}}$，则 $-\lambda$ 对应特征向量 $x^{\prime }={\left(x_1,\cdots ,x_s,-y_1,\cdots ,-y_t\right)}^{\text{T}}$。

3. 一类星形树的主特征值数目

定理3.1 星形树 $S\left(1,1,m\right)$ $\left(m\ge 1\right)$ 的主特征值数目有以下情况：当m为偶数时， $S\left(1,1,m\right)$ 的主特征值数大于等于 $\frac{m}{2}+1$，其中0是单根且为非主特征值；当m为奇数时，非零特征值 $\pm \lambda$ 同为主特征值或同为非主特征值，且0是二重根，进一步当 $m=4k-3$ 时，0为非主特征值；当 $m=4k-1$ 时，0为主特征值 $\left(k\ge 1\right)$。

证明：首先分析图 $S\left(1,1,m\right)$ 根的情况，因为 $\lambda =\left\{0\right\}\cup \left\{2\cos \left(\frac{2k+1}{2m+4}\pi \right),k=0,1,\cdots ,m+1\right\}$，而 $\frac{2k+1}{2m+4}=\frac{1}{2}$ 当且仅当 $k=\frac{m+1}{2}$，说明只有m为奇数即 $\left|V\left(S\left(1,1,m\right)\right)\right|=m+3$ 为偶数时，0是 $S\left(1,1,m\right)$ 的二重根，m为偶数时0为单根。因为余弦值 $\cos \theta$ 在区间 $\left[0,\pi \right]$ 上单调递减，故图 $S\left(1,1,m\right)$ 的非零特征值均为单根，且关于原点对称。

设图 $S\left(1,1,m\right)$ 的邻接矩阵为 $A={\left(\begin{array}{ccccccc}0& 0& 1& 0& \cdots & 0& 0\\ 0& 0& 1& 0& \cdots & 0& 0\\ 1& 1& 0& 1& \cdots & 0& 0\\ 0& 0& 1& 0& \cdots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& 0& \cdots & 0& 1\\ 0& 0& 0& 0& \cdots & 1& 0\end{array}\right)}_{n\times n}$，易见 $n=m+3$。对其特征值 $\lambda$ 及对应特征向量x有 $Ax=\lambda x$，令 $x={\left(x_1,x_2,\cdots ,x_n\right)}^{\text{T}}$，展开方程得到：

$\{\begin{array}{l}{x}_3=\lambda x_1\\ x_3=\lambda x_2\\ x_1+x_2+x_4=\lambda x_3\\ x_3+x_5=\lambda x_4\\ x_4+x_6=\lambda x_5\\ \cdots \\ x_{n-2}+x_n=\lambda x_{n-1}\\ x_{n-1}=\lambda x_n\end{array}$ (1)

由(1)式可知，A的每一个特征向量x都可以由最后一个分量 $x_n\left(\ne 0\right)$ 表示，不妨设 $x_n=1$。

若 $x_n=0$，则代入(1)式可得：

$\{\begin{array}{l}{x}_1+x_2=0\\ x_n=x_{n-1}=x_{n-2}=x_{n-3}=\cdots =x_5=x_4=x_3=0\end{array}$

故易见向量 $x^{\prime }={\left(1,-1,0,\cdots ,0\right)}^{\text{T}}$ 是对应特征值0的特征向量，即满足 $A{x}^{\prime }=0\cdot x^{\prime }$，由 $e^{\text{T}}{x}^{\prime }=0$ 知0是非主特征值，且该0特征值不由 $2\cos \left(\frac{2k+1}{2m+4}\pi \right)$ 贡献。

将(1)式左右两端相加得：

$2{\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}-x_1-x_2+x_3-x_n=\lambda {\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}$

化简得：

$\left(2-\lambda \right){\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}=x_1+x_2-x_3+x_n$

因为 $\lambda \in \left(-2,2\right)$，$2-\lambda >0$，故 ${\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}=0$ 即 $\lambda$ 为非主特征值当且仅当

$x_1+x_2-x_3+x_n=0$ (2)

下面讨论 $\lambda \ne 0$ 的情况。

此时显然 $x_1\ne 0$，否则有 $x_n=x_{n-1}=x_{n-2}=x_{n-3}=\cdots =x_5=x_4=x_3=x_2=x_1=0$，向量x无意义。

由(1)式知 $x_n\ne 0$ 时，有 $x_1=x_2$，故(2)式可表示为：

$\left(2-\lambda \right)x_1+1=0$ (3)

因为 $2-\lambda >0$，故当 $x_1>0$ 时(3)式左端恒大于零，等式矛盾，说明 $x_1>0$ 时 ${\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}\ne 0$，对应特征值 $\lambda$ 为主特征值。

1) 当 $m$ 为偶数时， $n=m+3$ 为奇数，对于特征值 $\pm \lambda$，若对应 $\lambda$ 的特征向量为 $x={\left(x_1,x_2,\cdots ,x_{n-1},1\right)}^T$，因为 $S\left(1,1,m\right)$ 为二部图，连接在中心点 $v$ 的两个一度点和 $P_m$ 中与 $v$ 的距离为奇数的顶点可划分为一个顶点集，则由推论2.8可得对应 $-\lambda$ 的特征向量为 $y={\left(-x_1,-x_2,x_3,-x_4,x_5,\cdots ,x_{n-2},-x_{n-1},1\right)}^{\text{T}}$，$x$ 和 $y$ 的第一个分量异号且不等于0，则 $\pm \lambda$ 至少有一个为主特征值，这就说明对于奇数个顶点的图 $S\left(1,1,m\right)$，其至少有 $\frac{m+3-1}{2}$ 个主特征值。

2) 当 $m$ 为奇数时， $n=m+3$ 为偶数，对于特征值 $\pm \lambda$，若对应 $\lambda$ 的特征向量为 $x={\left(x_1,x_2,\cdots ,x_{n-1},1\right)}^{\text{T}}$，同理可得对应 $-\lambda$ 的特征向量为 $y={\left(x_1,x_2,-x_3,x_4,-x_5,\cdots ,-x_{n-2},x_{n-1},1\right)}^{\text{T}}$，$x$ 和 $y$ 的第一个分量同号且不等于0，说明对于偶数个顶点的图 $S\left(1,1,m\right)$，其特征值 $\pm \lambda$ 同为主特征值(或非主特征值)。

最后讨论0作为二重根出现的情况。

由上面分析可知当 $m$ 为奇数，0是二重根，且其中一个0对应特征向量 $x^{\prime }={\left(1,-1,0,\cdots ,0\right)}^{\text{T}}$。

将 $x_n=1$ 代入(1)式并化简得：

$\{\begin{array}{l}{x}_3=\lambda x_4-x_5\\ x_4=\lambda x_5-x_6\\ \cdots \\ x_{n-2}=\lambda x_{n-1}-x_n\\ x_{n-1}=\lambda \\ x_n=1\end{array}$

观察可得向量 $x={\left(x_1,x_2,\cdots ,x_n\right)}^{\text{T}}$ 的分量满足递推关系 $x_t=\lambda x_{t+1}-x_{t+2}\left(t=3,4,\cdots ,n-2\right)$，且初始值 $x_n=1$，$x_{n-1}=\lambda$。则对比路 $P_n$ 的特征多项式可得：

$\{\begin{array}{l}{\phi }_{n-3}\left(\lambda \right)=x_3\\ {\phi }_{n-4}\left(\lambda \right)=x_4\\ \cdots \\ {\phi }_2\left(\lambda \right)=x_{n-2}\\ {\phi }_1\left(\lambda \right)=x_{n-1}\\ {\phi }_0\left(\lambda \right)=x_n\end{array}$

故由 $x_1+x_2+x_4=\lambda x_3$ 可得：

$x_1+x_2=\lambda x_3-x_4\Rightarrow x_1+x_2=\lambda {\phi }_{n-3}\left(\lambda \right)-{\phi }_{n-4}\left(\lambda \right)={\phi }_{n-2}(\; \lambda \; )$

代入(2)式有 ${\phi }_{n-2}\left(\lambda \right)+1=0$ (此时 $x_3=\lambda x_1=0$ )。

由 ${\phi }_n\left(x\right)$ 的奇偶性可得，

${\phi }_0\left(0\right)=1,{\phi }_1\left(0\right)=0,{\phi }_2\left(0\right)=-1,{\phi }_3\left(0\right)=0,{\phi }_4\left(0\right)=1,\cdots ,{\phi }_{4t}\left(0\right)=1,{\phi }_{4t+2}\left(0\right)=-1,\left(t=0,1,\cdots \right)$

故当 $n=4k+2$ 时， ${\phi }_{4k+2-2}\left(0\right)+1=2>0$，$0$ 为主特征值；当 $n=4k$ 时， ${\phi }_{4k-2}\left(0\right)+1=-1+1=0$，$0$ 为非主特征值，其中 $k\ge 1$。

定义3.2 [1] 对于一个图 $G$，若其顶点集可划分为 $V\left(G\right)=V_1\cup V_2\cup \cdots \cup V_k$，$V_i\cap V_i$ 为空集，其中 $V_i$ 中的每个顶点在 $V_j$ 中的邻点个数相同，记为 $b_{ij}$，$i,j\in \left\{1,2,\cdots ,k\right\}$，则称该划分为图G的一个公平划分，记为 $\Pi$。以 $V_1,V_2,\cdots ,V_k$ 为顶点集， $V_i$ 到 $V_j$ 有 $b_{ij}$ 条弧的有向多重图称为图G的商图，矩阵 $B={\left(b_{ij}\right)}_{k\times k}$ 称为商矩阵。

定理3.3 [1] 对于图G的任意商图H，H的谱包含G的全部主特征值。

对于任意图G的一个公平划分 $\Pi$ 来说，因为每个划分 $V_i$ 内的顶点处于G自同构群中的同一轨道，故由定理3.3可知，对于恰有k个主特征值的图，其自同构群至少有k条轨道。

推论3.4 星形树 $S\left(m_1,\cdots ,m_1,m_2,\cdots ,m_2,\cdots ,m_s,\cdots ,m_s\right)$ 至多有 $m_1+m_2+\cdots +m_s+1$ 个主特征值，其中 $m_1,\cdots ,m_s$ 的个数分别为 $t_1,\cdots ,t_s\left(t_i\ge 1\right)$。

证明：显然星形树 $S\left(m_1,\cdots ,m_1,m_2,\cdots ,m_2,\cdots ,m_s,\cdots ,m_s\right)$ 的顶点数为 $t_1{m}_1+t_2{m}_2+\cdots +t_s{m}_s+1$，我们可以找到其阶数最小的商图H，点集划分如下：首先将长度相同的 $P_{m_i}$ 分为一组，其中每条路 $P_{m_i}$ 中与中心点 $v$ 距离相同的点处于同一轨道，故可将同一轨道中的 $t_i$ 个顶点划分为一个顶点集，因此对每组 $P_{m_i}$ 来说，其可划分为因子图H中的 $m_i$ 个顶点。同理每组 $P_{m_i}$ 均可划分为H中的 $m_i$ 个顶点，又中心点 $v$ 自处一个轨道，故H的阶为 $m_1+m_2+\cdots +m_s+1$。由定理3.3知，任意商图的谱包含原图的全部主特征值，故星形树 $S\left(m_1,\cdots ,m_1,m_2,\cdots ,m_2,\cdots ,m_s,\cdots ,m_s\right)$ 至多有 $m_1+m_2+\cdots +m_s+1$ 个主特征值。

文章引用

杜泽楠,于 倩. 一类树的主特征值数目刻画
Characterization of the Number of Main Eigenvalues of a Class of Trees[J]. 运筹与模糊学, 2021, 11(02): 131-136. https://doi.org/10.12677/ORF.2021.112016

参考文献