Advances in Applied Mathematics
Vol.06 No.06(2017), Article ID:22107,7
pages
10.12677/AAM.2017.66087
Positive Periodic Solutions for a Class of Delayed Neoclassical Growth Model
Chunyu Yang, Ruojun Zhang, Jingjing Zhang
School of Mathematical Sciences, Ocean University of China, Qingdao Shandong
Received: Aug. 25th, 2017; accepted: Sep. 11th, 2017; published: Sep. 19th, 2017

ABSTRACT
In this paper, the existence of positive periodic solutions for a class of delayed neoclassical growth model with impulse is considered. By using the cone fixed point theorem, some sufficient conditions of the existence of positive periodic solutions for the addressed model are obtained. Moreover, an example is given to show the effectiveness of our results.
Keywords:Neoclassical Growth Model, Positive Periodic Solutions, Delay, Impulse
时滞脉冲新古典增长模型的正周期解
杨春雨,张若军,张静静
中国海洋大学数学科学学院,山东 青岛
收稿日期:2017年8月25日;录用日期:2017年9月11日;发布日期:2017年9月19日

摘 要
本文考虑了一类具有脉冲项的时滞新古典增长模型的正周期解问题,利用锥拉伸与锥压缩不动点定理给出了该模型存在两个不同正周期解的条件,并通过实例验证了所得结论的有效性。
关键词 :新古典增长模型,正周期解,时滞,脉冲

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
20世纪50年代,索洛等人 [1] [2] 提出形如
的新古典增长模型,其中
为 时期的总产出,
为
时期投入的资本量,
为
时期投入的劳动量,
代表
时期的技术水平,由于具有预见性与实用性,该模型被众多学者所关注。Day [3] [4] [5] ,Puu [6] ,Bischi [7] 等人进一步研究了新古典增长模型等非线性经济动力系统,并对之有极大的创新和发展。依据经济学原理,为描述长时间经济行为,新古典增长模型有两个基本假设:一是劳动力和资本充分;二是输出市场的即时调整。然而,由于生产过程中时滞的不可避免,所以这种理想的假设在现实中是不合理的,因此有必要考虑时滞系统。
时期的总产出,
为
时期投入的资本量,
为
时期投入的劳动量,
代表
时期的技术水平,由于具有预见性与实用性,该模型被众多学者所关注。Day [3] [4] [5] ,Puu [6] ,Bischi [7] 等人进一步研究了新古典增长模型等非线性经济动力系统,并对之有极大的创新和发展。依据经济学原理,为描述长时间经济行为,新古典增长模型有两个基本假设:一是劳动力和资本充分;二是输出市场的即时调整。然而,由于生产过程中时滞的不可避免,所以这种理想的假设在现实中是不合理的,因此有必要考虑时滞系统。
2011年,Matsumoto和Szidarovszky [8] 首次介绍了如下的时滞新古典增长模型
(1.1)
其中
是人均资本,
为平衡储蓄倾向,
,其中
为资本折旧率,
为劳动增长率,生产函数
(
和
是正参数),
为生产过程中的时滞。2013年,Matsumoto和Szidarovszky [9] 将模型(1.1)修改成如下形式
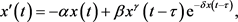 (1.2)
(1.2)
其中
为正参数,
代表资本集中度提高带来的消极影响的强度,
代表生产规模报酬率,且
,
为正常数。Matsumoto和Szidarovszky考虑了模型(1.2)分别在
时的局部稳定性。
现实生活中的系统会受到各种突发状况的影响,因此脉冲在动力系统中需加以考虑。二十世纪八十年代后,脉冲微分方程理论得到快速发展,研究成果日益丰富,可以参看文献 [11] [12] 。
本文将考察一类具有脉冲项的时滞新古典增长模型的正周期解问题,这方面的研究目前尚未见报道。
2. 预备知识
考虑如下脉冲时滞新古典增长模型
(2.1)
其中
,
,
,
为正参数,
为脉冲点。
模型(2.1)具有初值条件
(2.2)
其中
。
对于(2.1)与(2.2),提出如下假设:
H1)
是以
为周期的周期函数,
;
H2)
,
为给定的脉冲时刻,
;
H3)
为实数列,
;
H4)
为以
为周期的周期函数(这里作一个标准的假设,若因子个数为0,则乘积为1);
H5)
。
定义2.1:称定义在
上的函数
为模型(2.1)在初值条件(2.2)下的解,若
满足如下条件
i)
在
与
上绝对连续;
ii)
与
存在且
;
iii)
在
上几乎处处满足方程(2.1),在
满足脉冲条件;
iv)
。
在假设条件(H1)~(H5)下,考虑如下模型
(2.3)
其中
,
。
模型(2.3)满足初值条件
(2.4)
是模型(2.3)在初值条件(2.4)下的解,是指
是定义在
上,在
上是满足(2.3)的绝对连续函数,且在
上满足初值条件(2.4)。
定义2.2 [13] :设
为Banach空间,
称为
中的一个锥,如果它是
的非空闭子集,且满足条件
i)
ii)
蕴含
。
引理2.1 [13] (锥拉伸与锥压缩不动点定理)
设
为Banach空间
中的有界开子集,
,
为
中的一个锥,
为全连续算子,若
满足条件:
i)
(即范数锥拉伸);
ii)
(即范数锥压缩)。
则
在
中必存在不动点。
3. 主要结果
引理3.1:假设(H1)~(H5)成立,则
i)
为模型(2.3)与(2.4)的解,则
为模型(2.1)与(2.2)在
上的解;
ii)
为模型(2.1)与(2.2)的解,则
为模型(2.3)与(2.4)在
上的解。
证明:i) 设
为模型(2.3)与(2.4)的解,易知
在
及
上绝对连续,且对
,有
所以,
在
上几乎处处满足方程(2.1)。
对每个
,有
因此,对于每个
有
。
且在
上,有
。因此
为模型(2.1)与(2.2)在
上的解。
ii)设
是模型(2.1)与(2.2)的解,所以
在
与
上是绝对连续的。因此,
在
与
上也是绝对连续的。
对
,有
,
且
,则
是连续的且易知在
上绝对连续,由(i)类似可证
为(2.3)在
上满足初值条件(2.4)的解。
推论3.1:假设条件(H1)~(H5)成立,则
i)
为(2.3)与(2.4)的
-周期解,则
为(2.1)与(2.2)在
上的正
-周期解;
ii)
为(2.1)与(2.2)的
-周期解,则
为(2.3)与(2.4)在
上的正
-周期解。
证明:由引理3.1以及假设条件(H1),(H4)即可得证。
注3.1:由推论3.1可知,讨论具有脉冲影响的时滞新古典增长模型(2.1)的
-正周期解,只需要转化为讨论不具有脉冲的时滞新古典增长模型(2.3)的
-正周期解。
为应用引理2.1,令
,赋予范数
,则
为Banach空间。
令
,其中
为后面所定义的正常数,则
为
中的锥。定义算子
(3.1)
其中
,
,
。记
以下为方便计,对于
-周期函数
,采用如下符号
,
。
注3.2:由引理2.1知,对于
,
是
上的全连续算子,且易证模型(2.3)的正
-周期解的存在性等价于求
在
上的不动点。
注3.3:引入函数
,则易知
在
上严格单调递增,在
上严格单调递减,则知
在点
取得最大值,且存在唯一的
,使得
。
引理3.2:假设条件(H1)~(H5)成立,则
为全连续算子。
证明:由假设,
为连续的
-周期函数。且易验证
,
,有
,
所以,
。因此
。
下证
为全连续的。显然
是连续的。又,可得
,
以及,
因此
是紧的,从而
为全连续的。
定理3.1:假设条件(H1)~(H5)成立,再假设条件(H6)
成立,则方程(2.3)在初值条件(2.4)下存在两个正周期解。
证明:因为
,则存在两个正常数
Math_190#,以及存在一个充分小满足
的
,使得
(3.2)
(3.3)
定义
,当
时,有
且
,由(3.1)和(3.2),得
,
因此,
,
。
定义
,当
时,有
,
,因为
,从而由条件(H6),有
因此,
,
。
定义
,其中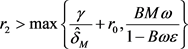 ,
,
,当
时,有
,
。则由(3.1)和(3.3),得
因此,
,
,其中
,
。
因为
,且由引理3.2知,
,
是全连续的,因此,由引理2.1,得到
在
上存在不动点
,在
上存在另一个不动点
。又因为
,
,因此
与
为模型(2.3)在初值条件(2.4)下的两个不同的正周期解。
由引理3.1,可知模型(2.1)在初值条件(2.2)下存在两个不同的正周期解。
4. 具体实例
考虑下列脉冲时滞新古典增长模型
(4.1)
其中取脉冲
,脉冲时刻为
。令
,则有
因此
是以
为周期的函数。
由
,
,
,
,
,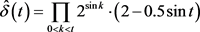 ,
,
,易知,
是以
为周期的周期函数,
,
,
,
,
,
,
,则有
,从而定理3.1的条件满足。因此,由定理3.1,知模型(4.1)存在两个
-正周期解。
,
,
,易知,
是以
为周期的周期函数,
,
,
,
,
,
,
,则有
,从而定理3.1的条件满足。因此,由定理3.1,知模型(4.1)存在两个
-正周期解。
文章引用
杨春雨,张若军,张静静. 时滞脉冲新古典增长模型的正周期解
Positive Periodic Solutions for a Class of Delayed Neoclassical Growth Model[J]. 应用数学进展, 2017, 06(06): 727-733. http://dx.doi.org/10.12677/AAM.2017.66087
参考文献 (References)
- 1. Solow, R. (1956) A Contribution to the Theory of Economic Growth. Quarterly Journal of Economics, 98, 203-213.
https://doi.org/10.2307/1884513
- 2. Swan, T. (1956) Economic Growth and Capital Accumulation. Quarterly Journal of Economics, 70, 65-94.
https://doi.org/10.1111/j.1475-4932.1956.tb00434.x
- 3. Day, R. (1983) Irregular Growth Cycles. American Economic Review, 72, 406-414.
- 4. Day, R. (1983) The Emergence of Chaos from Classical Economic Growth. Quarterly Journal of Economics, 98, 203-213. https://doi.org/10.2307/1885621
- 5. Day, R. (1994) Complex Economic Dynamics: An Introduction to Dynamical Systems and Market Mechanism. MIT Press, Cambridge.
- 6. Puu, T. (2003) Attractions, Bifurcations and Chaos: Nonlinear Phe-nomena in Economics. Springer, Berlin.
https://doi.org/10.1007/978-3-540-24699-2
- 7. Bischi, G.I., Chiarella, C., Kopel, M. and Szidarovszky, F. (2000) Nonlinear Oligopolies: Stability and Bifurcation. Springer, Berlin.
- 8. Matsumoto, A. and Szidarovszky, F. (2011) Delay Differential Neoc-lassical Growth Model. Journal of Economic Behavior & Organization, 78, 272-289. https://doi.org/10.1016/j.jebo.2011.01.014
- 9. Matsumoto, A. and Szidarovszky, F. (2013) Asymptotic Behavior of a Delay Differential Neoclassical Growth Model. Sustainability, 5, 440-455. https://doi.org/10.3390/su5020440
- 10. Lakshmikantham, V., Dimitŭr, B. and Pavel, S. (1989) Theory of Impulsive Differential Equations. World scientific, Singapore. https://doi.org/10.1142/0906
- 11. Bainov, D. and Simeonov, P. (1993) Impulsive Differential Equations: Periodic Solutions and Applications. Longman Scientific and Technical, New York.
- 12. Bainov, D.D. and Simeonov, P.S. (1995) Impulsive Differential Equations: Asymptotic Properties of the Solutions. World Scientific, Singapore. https://doi.org/10.1142/2413
- 13. 郭大钧. 非线性泛函分析[M]. 济南: 山东科学技术出版社, 2001.





 时期的总产出,
为
时期投入的资本量,
为
时期投入的劳动量,
代表
时期的技术水平,由于具有预见性与实用性,该模型被众多学者所关注。Day [3] [4] [5] ,Puu [6] ,Bischi [7] 等人进一步研究了新古典增长模型等非线性经济动力系统,并对之有极大的创新和发展。依据经济学原理,为描述长时间经济行为,新古典增长模型有两个基本假设:一是劳动力和资本充分;二是输出市场的即时调整。然而,由于生产过程中时滞的不可避免,所以这种理想的假设在现实中是不合理的,因此有必要考虑时滞系统。
时期的总产出,
为
时期投入的资本量,
为
时期投入的劳动量,
代表
时期的技术水平,由于具有预见性与实用性,该模型被众多学者所关注。Day [3] [4] [5] ,Puu [6] ,Bischi [7] 等人进一步研究了新古典增长模型等非线性经济动力系统,并对之有极大的创新和发展。依据经济学原理,为描述长时间经济行为,新古典增长模型有两个基本假设:一是劳动力和资本充分;二是输出市场的即时调整。然而,由于生产过程中时滞的不可避免,所以这种理想的假设在现实中是不合理的,因此有必要考虑时滞系统。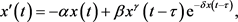 (1.2)
(1.2)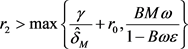 ,
,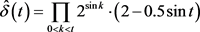 ,
,
,易知,
是以
为周期的周期函数,
,
,
,
,
,
,
,则有
,从而定理3.1的条件满足。因此,由定理3.1,知模型(4.1)存在两个
-正周期解。
,
,
,易知,
是以
为周期的周期函数,
,
,
,
,
,
,
,则有
,从而定理3.1的条件满足。因此,由定理3.1,知模型(4.1)存在两个
-正周期解。