Dynamical Systems and Control
Vol.
08
No.
03
(
2019
), Article ID:
31246
,
10
pages
10.12677/DSC.2019.83020
Bifurcation Analysis of a Predator-Prey Model with Constant Prey Harvesting
Guihua Zou, Xuanliang Liu
School of Mathematics, South China University of Technology, Guangzhou Guangdong

Received: Jun. 19th, 2019; accepted: Jun. 29th, 2019; published: Jul. 12th, 2019

ABSTRACT
In this paper, we study the bifurcation of a predator-prey model with constant prey harvesting rate. By using the qualitative and bifurcation theory of ordinary differential equations, we analyze the existence conditions of equilibria, and discuss the Hopf and Bogdanov-Takens bifurcations near positive equilibria, respectively. The conditions and conclusions of corresponding bifurcations are obtained.
Keywords:Predator-Prey Model, Harvesting Rate, Hopf Bifurcation, Bogdanov-Takens Bifurcation
一类具有常数收获率的捕食者–食饵模型的 分支分析
邹桂华,刘宣亮
华南理工大学数学学院,广东 广州

收稿日期:2019年6月19日;录用日期:2019年6月29日;发布日期:2019年7月12日

摘 要
本文研究一类食饵种群具有常数收获率的捕食者–食饵模型的分支问题。利用常微分方程的定性与分支理论,分析了模型平衡点的存在条件,主要讨论了正平衡点的Hopf分支和Bogdanov-Takens分支,并得出了相应分支产生的条件及其结论。
关键词 :捕食者–食饵模型,收获率,Hopf分支,Bogdanov-Takens分支

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
近几十年来,人们对种群动力学模型进行了广泛的研究,特别是关于捕食者–食饵模型的研究,得到了大量的结论 [1] - [8] 。例如,对具有常数收获率的捕食者–食饵模型,文 [2] [3] [4] 进行了研究,讨论了模型的各种分支现象。文 [5] [6] [7] 考虑了疾病在捕食者种群或食饵种群中传播的捕食者–食饵模型,研究了模型平衡点的稳定性和分支行为。虽然对捕食者–食饵模型有很多的研究工作,但经典的捕食者–食饵模型仍存在一些不足的地方。例如文 [8] 考虑了由于食饵种群对捕食者种群的恐惧会造成食饵种群出生率的下降,于是对食饵种群的出生率引入了恐惧效应因子 ,其中y为捕食者种群密度,k为与恐惧水平有关的常数,即将原来食饵种群的出生率 修改为与捕食者种群密度有关的出生率: ,然后研究了捕食者–食饵模型的动力学性质。
受文 [8] 的启发,对食饵种群具有常数收获率的Leslie-Gower类捕食者–食饵模型 [2] [3] ,我们在食饵种群的出生率中也引入文 [8] 中考虑过的恐惧效应因子: ,即考虑如下的捕食者–食饵模型:
(1)
其中:x为食饵种群的密度,y为捕食者种群的密度, 为食饵种群的出生率, 为捕食者种群的内
禀增长率,ax为每一个捕食者捕食食饵的数量,bx为捕食者种群中与食饵有关的容纳量,c为食饵种群内部竞争的死亡率,d为食饵种群的自然死亡率,h为捕食者对食饵的常数收获率。所有参数都为正参数。
首先对模型(1)作如下的变换
则可将模型(1)变为
(2)
其中: 。
2. 平衡点及其类型
考虑到模型(1)的生物意义,下面我们的讨论都在 上进行。首先考虑平衡点的存在性。令系统(2)右端为0,可得:
1) 若 ,则有
(3)
记 。
i) 当
且 时,则系统(2)有唯一边界平衡点
。
时,则系统(2)有唯一边界平衡点
。
ii) 当 且 时,则系统(2)有两个边界平衡点
和
2) 若 ,则 ,且
(4)
记 ,则有
当 时,记
则 为 的唯一正根。如下结论成立:
i) 当 时,系统(2)有唯一正平衡点 。
ii) 当 时,系统(2)有两个正平衡点 和 ,其中 。
通过讨论系统(2)在平衡点处的Jacobi矩阵的特征值,利用文 [9] [10] ,可得如下结论: 为一个鞍结点, 为不稳定的非鞍初等奇点, 为鞍点, 为高次奇点, 为鞍点, 为非鞍初等奇点。
3. Hopf分支
由上一节可知,当 且 时,系统(2)有两个正平衡点 和 ,其中 是鞍点, 为初等焦点或结点。下面讨论系统(2)在 附近的Hopf分支。
系统(2)在 处的雅可比矩阵为:
其中 , 。则矩阵A的特征方程为
. (5)
当 时,矩阵A的特征方程(5)有一对纯虚根 (i为虚数单位, )。由 是系统(2)的平衡点以及 可得
(6)
由辗转相除法,可得
将 代入 ,得到A的特征根有一对纯虚根的条件: 且
取 为分支参数。设特征方程(5)的特征根为: ,则有 。由于 ,则由 确定的隐函数 的导数: ,又 ,于是有
.
由 知系统(2)产生Hopf分支的横截条件 [11] 满足,因此系统(2)在 附近可产生Hopf分支。而且,当 时,平衡点 是稳定的,当 时,平衡点 是不稳定的。下面讨论Hopf分支的方向。
令 , ,则系统(2)变成以下形式
(7)
再作变换:
系统(7)变为
引入复变量: ,可以得到:
其中:
将上述结果代入一阶Lyapunov系数的计算公式 [11]
可得
因此,由文 [11] 可得以下结论:
i) 当 时,模型(1)在 附近有超临界的Hopf分支产生;
ii) 当 时,模型(1)在 附近有次临界的Hopf分支产生。
例如,取 ,则 , , ,可算出 。于是系统(2)在 时产生超临界的Hopf分支。当 在大于 附近取值时,在平衡点 附近存在唯一稳定极限环。如图1(a)所示。若取 ,则 , , ,可算出 ,于是系统(2)在 处产生次临界的Hopf分支。当 在小于 附近取值时,在平衡点 附近存在唯一不稳定极限环。如图1(b)所示。
4. Bogdanov-Takens分支
当 且 时,系统(2)在正平衡点 处的特征方程(5)有两个零特征值,此时 满足方程组(6)及
利用辗转相除法,最终可得到特征方程(5)有两个零特征值的参数条件:
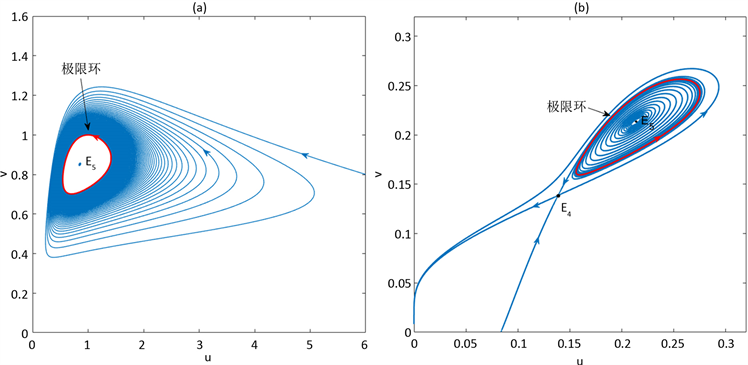
Figure 1. (a) When , there is a stable limit cycle near ; (b) When , there is a unstable limit cycle near
图1. (a) 当 时,在 附近有一个稳定极限环;(b) 当 时,在 附近有一个不稳定极限环
我们选取 作为分支参数,讨论系统(2)在 附近的Bogdanov-Takens分支问题。
记 , , , 。于是系统(2)可以写成
其中 。 在 处的泰勒展开式为
其中
设有二阶可逆矩阵 ,使得 。可取
再设 ,可得
利用文献 [12] 中的记号,通过计算,不难得到:
其中
记 , ,则
由文献 [12] 可知,当 时,系统(2)在正平衡点 附近的中心流形上的轨线行为局部拓扑等价于以下系统
(8)
由于 ,再作变量变换
于是系统(8)变为
(9)
其中: , 。对系统(9),利用文 [11] 中关于Bogdanov-Takens分支的讨论,可知,当 时,系统(9)在原点附近有以下分支现象:
i) 有鞍结点分支曲线: ;
;
ii) 有Hopf分支曲线: ;
iii) 有同宿分支曲线: 。
例如,取参数 时,可算出 , ,当 时,系统(2)在正平衡点 处有两个零特征值。当 时,在 附近有Bogdanov-Takens分支产生。出现的鞍结点分支曲线SN,Hopf分支曲线H与同宿分支曲线HL将整个参数平面 分为四个区域,分别为图2(a)中区域①~④。下面在 附近适当选取几组参数值 ,使得 分别位于每一个区域上,并作出系统(2)对应的相图。
取 。当 时, ①,此时系统(2)的相图如图2(b)所示,系统(2)无正平衡点;当 时, ②,此时系统(2)的相图如图2(c)所示;当 时, ③,此时系统(2)的相图如图2(d)所示,系统(2)有一个不稳定极限环(红色闭曲线)出现;当 时, ④,此时系统(2)的相图如图2(e)所示;当 时, ,此时系统(2)的相图如图2(f)所示,系统(2)有一条同宿轨(红色曲线)出现。
5. 结论
文 [8] 中给出了具有恐惧效应的捕食者–食饵模型,讨论了模型的平衡点的稳定性,极限环的存在性和余维1的Hopf分支。本文对食饵种群进一步增加常数收获率后进行分析,发现模型除了有余维1的Hopf分支外,还会产生余维2的Bogdanov-Takens分支。本文对这两种分支现象分别进行了研究,并作出了相应的相图和分支图,作图时使用了Matlab软件和Matcont软件。由本文的结论可看出,通过Hopf分支可产生极限环,其中超临界Hopf分支可产生稳定极限环,表明参数和初值的适当选取,可使捕食者和食饵种群数量最终呈周期性变化而不消失。次临界Hopf分支可产生不稳定极限环,表明当初值位于不稳

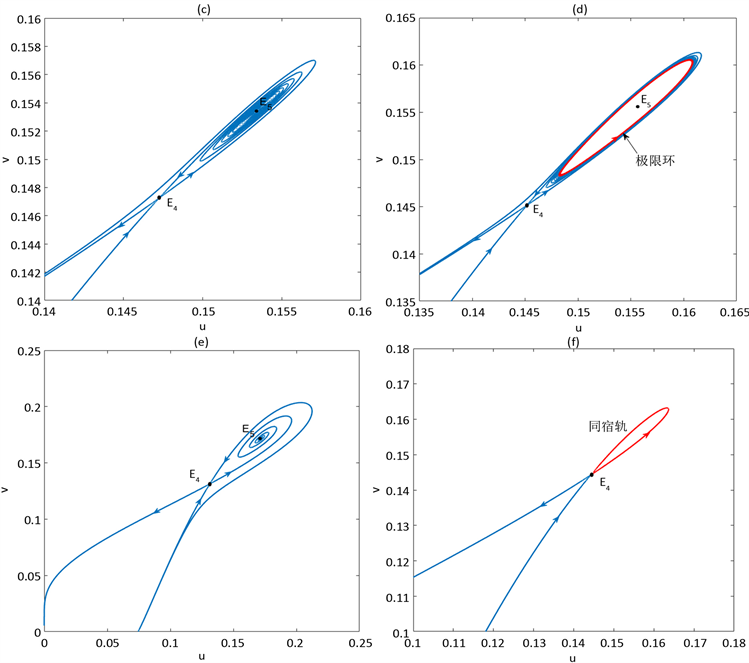
Figure 2. When α = 0.6, β = 5, θ = 0.2, h0 = 0.1690754631, taking r = 2.464799684, 2.492799684, 2.493799684, 2.514799684, 2.494410328, the phase portraits corresponding to system (2) are (b), (c), (d), (e), (f), respectively, where there is an unstable limit cycle (red closed curve) in Figure (d), and there is a homoclinic orbit (red curve) in Figure (f)
图2. 当α = 0.6, β = 5, θ = 0.2, h0 = 0.1690754631时,分别取r = 2.464799684, 2.492799684, 2.493799684, 2.514799684, 2.494410328,系统(2)对应的相图分别为 (b), (c), (d), (e), (f), 其中在图(d)中有一个不稳定极限环(红色闭曲线)出现,在图(f)中有一条同宿轨(红色曲线)出现
定极限环内时,轨线趋向正平衡点E5,即捕食者和食饵种群数量最终趋于稳定而不消失。由Bogdanov-Takens分支可产生三种分支曲线SN,H和HL的结论,表明除了由Hopf分支产生极限环外,还可由鞍结点分支产生两个正平衡点,以及由同宿分支出现同宿轨和分支出不稳定极限环,当初值位于同宿轨或极限环内时,轨线趋于正平衡点E5,即参数和初值的适当选取,可使捕食者和食饵种群数量最终趋于稳定而不消失。
基金项目
国家自然科学基金(11572127)。
文章引用
邹桂华,刘宣亮. 一类具有常数收获率的捕食者–食饵模型的分支分析
Bifurcation Analysis of a Predator-Prey Model with Constant Prey Harvesting[J]. 动力系统与控制, 2019, 08(03): 181-190. https://doi.org/10.12677/DSC.2019.83020
参考文献
- 1. 马知恩. 种群生态学的数学建模与研究[M]. 合肥: 安徽教育出版社, 1996.
- 2. Zhu, C.R. and Lan, K.Q. (2010) Phase Portraits, Hopf Bifurcation and Limit Cycles of Leslie-Gower Predator-Prey Systems with Harvesting Rates. Discrete & Continuous Dynamical Systems-B, 14, 289-306.
https://doi.org/10.3934/dcdsb.2010.14.289 - 3. Gong, Y.J. and Huang, J.C. (2014) Bogdanov-Takens Bifurcation in a Leslie-Gower Predator-Prey Model with Prey Harvesting. Acta Mathematicae Applicatae Sinica, English Series, 30, 239-244.
https://doi.org/10.1007/s10255-014-0279-x - 4. Huang, J.C., Gong, Y.J. and Ruan S.G. (2013) Bifurcation Analysis in a Pred-ator-Prey Model with Constant-Yield Predator Harvesting. Discrete and Continuous Dynamical Systems-B, 18, 2101-2121.
https://doi.org/10.3934/dcdsb.2013.18.2101 - 5. Liu, X.L. (2011) Bifurcation of an Eco-Epidemiological Model with a Non-linear Incidence Rate. Applied Mathematics and Computation, 218, 2300-2309.
https://doi.org/10.1016/j.amc.2011.07.050 - 6. 刘宣亮, 江文超. 一类具有非线性发生率的生态-流行病模型分析[J]. 北华大学学报(自然科学版), 2016, 17(3): 281-289.
- 7. 刘宣亮, 王志星. 一类捕食者有传染病的捕食者-食饵模型的分支分析[J]. 北华大学学报(自然科学版), 2018, 19(3): 281-290.
- 8. Wang, X.Y., Zanette, L. and Zou, X.F. (2016) Modelling the Fear Effect in Predator—Prey Interactions. Journal of Mathematical Biology, 73, 1179-1204.
https://doi.org/10.1007/s00285-016-0989-1 - 9. 张芷芬, 丁同仁, 黄文灶, 董镇喜. 微分方程定性理论[M]. 北京: 科学出版社, 1985.
- 10. 马知恩, 周义仓. 常微分方程定性与稳定性方法[M]. 北京: 科学出版社, 2007.
- 11. Kuznetsov, Y.A. (1998) Elements of Applied Bifurcation Theory. 2nd Edition, Springer-Verlag, New York.
- 12. Carrillo, F.A., Verduzco, F. and Joaquin, D. (2010) Analysis of the Takens-Bogdanov Bifurcation on m-Parameterized Vector Fields. International Journal of Bifurcation and Chaos, 20, 995-1005.
https://doi.org/10.1142/S0218127410026277