Steiner对称化下双变量凸体算子stH(·+·)的性质 The Properties of the Bivariate Convex Body Operator stH(·+·) under Steiner Symmetrization

doi:10.12677/PM.2020.102017

Pure Mathematics
Vol. 10 No. 02 ( 2020 ), Article ID: 34248 , 5 pages
10.12677/PM.2020.102017

The Properties of the Bivariate Convex Body Operator $s t_{H} (\cdot + \cdot)$ under Steiner Symmetrization

Yifang Jiang

●How to Cite this Article

School of Mathematics and Information Science, Shaanxi Normal University, Xi’an Shaanxi

Received: Jan. 25^th, 2020; accepted: Feb. 13^th, 2020; published: Feb. 20^th, 2020

ABSTRACT

In this paper, a bivariate convex body operator and its properties will be characterized by using Steiner symmetrization method and Minkowski addition. Steiner symmetrization of convex bodies with respect to a given hyperplane H in $R^{n}$ has a very important property that if the sets C and D are two convex bodies of Euclidean n-space $R^{n}$ , there is a inclusion relation: $s t_{H} (C + D) \subseteq s t_{H} C + s t_{H} D$ . This property plays a key role in the concise proof of the classical Brunn-Minkowski inequality and the classical isoperimetric inequality by using the Steiner symmetrization method. In this paper, on the basis of this property, we further characterize the bivariate convex body operator $s t_{H} (\cdot + \cdot)$ and its properties.

Keywords:Convex Bodies, Steiner Symmetrization, Minkowski Addition

Steiner对称化下双变量凸体算子 $s t_{H} (\cdot + \cdot)$ 的性质

姜亦芳

陕西师范大学，数学与信息科学学院，陕西西安

收稿日期：2020年1月25日；录用日期：2020年2月13日；发布日期：2020年2月20日

摘要

本文利用凸体的Steiner对称化的性质，结合Minkowski加法刻画了一个双变量凸体算子，并研究了该算子的相关性质。给凸体关于给定的 $R^{n}$ 中的超平面H作Steiner对称可以得到一条很重要的性质，即设C和D是n维欧式空间 $R^{n}$ 中的两个凸体，有包含关系： $s t_{H} (C + D) \subseteq s t_{H} C + s t_{H} D$ 。该性质在利用Steiner对称化方法得到经典的Brunn-Minkowski不等式和经典的等周不等式的简洁证明中起到了关键作用。本文就是在该性质的基础之上刻画了双变量凸体算子 $s t_{H} (\cdot + \cdot)$ 及其性质。

关键词 :凸体，Steiner对称，Minkowski加法

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

在凸几何分析中，一个更对称的凸体在许多情况下具有更好的几何或分析性质。因此，研究将凸体转化为更对称的凸体的对称化方法是非常有意义的，比如文献 [1] 中对Steiner，Minkowski，Schwarz和中心对称进行了研究。而在众多凸体的对称化方法中，Steiner对称化可能是解决凸几何领域中的问题最为强大的对称化方法，比如，利用Steiner对称化方法可以得到经典的Brunn-Minkowski不等式和经典的等周不等式的简洁证明 [2]，其他相关的应用可以查阅文献 [1] [3] - [9]。这是因为Steiner对称化方法具有很多优良性质，比如，保凸性、保体积性、表面积不增性、周长不增性等。在Brunn-Minkowski理论中，Minkowski加法是其重要的组成部分，比如经典的Brunn-Minkowski不等式就是建立在Minkowski加法的基础之上。

Steiner对称化关于Minkowski加法有一条非常重要的性质：设凸体 $C, D \in K^{n}$ ，对于给定 $R^{n}$ 中的超平面H，有以下的包含关系(即命题2.1 ii))：

$s t_{H} (C + D) \subseteq s t_{H} C + s t_{H} D,$

这条性质在利用Steiner对称化方法得到的经典的Brunn-Minkowski不等式和经典的等周不等式的简洁证明中都起到了至关重要的作用。本文就是以此为切入点，刻画了由该性质衍生出的双变量凸体算子 $s t_{H} (\cdot + \cdot)$ 及其相关性质，例如连续性、单调性等。

上述出现的概念和符号在下文中有详尽的说明。

2. 预备知识

本文首先回顾Steiner对称和Minkowski加法的定义和相关性质。我们以下的讨论基于n维实欧几里德向量空间 $R^{n}$ ，以o为原点， $〈 \cdot, \cdot 〉$ 为欧几里得空间的标准内积， $| \cdot |$ 为该内积诱导的范数。

设 $K^{n}$ 为 $R^{n}$ 上全体凸体(紧凸集)组成的集合(简称凸体空间)， $C^{n}$ 为 $R^{n}$ 上所有非空紧子集组成的集合(简称真凸体空间)，H为 $R^{n}$ 中的任意超平面。令 $C \in K^{n}$ ，则C关于超平面H的Steiner 对称化为 $s t_{H} C$ 的定义 [1] 为：对于每一条垂直于H的直线L，并且满足 $C \cap L \neq \emptyset$ ，将线段 $C \cap L$ 沿着L移动，直到 $C \cap L$ 的中点落在H上，这样得到的所有线段的并就是 $s t_{H} C$ 。显然， $s t_{H} C$ 关于超平面H(镜面)对称。

给定一个凸体 $C \in K^{n}$ ，我们给出一些刻画凸体的几何量的概念，直径 $d i a m (C) = \sup {| x - y | : x, y \in C}$ ，外接圆半径 $R (C) = \inf {R \in R : x + R B^{n} \supseteq C, x \in C}$ ，内切圆半径 $r (C) = \sup {r \in R : x + r B^{n} \subseteq C, x \in C}$ 。其中 $B^{n} = B (o, 1) = {x \in R : | x | \leq 1}$ 为 $R^{n}$ 中的实心单位球。

下面我们列出有关Steiner对称的性质定理，这些性质会在后文的证明中用到。

命题 2.1 [2] 凸体 $C, D \in K^{n}$ ，关于给定的超平面H的Steiner对称化具有以下的性质：

i) $s t_{H} C \in K^{n}$ ；

ii) $s t_{H} (C + D) \subseteq s t_{H} C + s t_{H} D$ ；

iii) 若 $C \subseteq D$ ，则有 $s t_{H} C \subseteq s t_{H} D$ ；

iv) 映射 $s t_{H} : C^{n} \to C^{n}$ 是连续的；

v) $d i a m (s t_{H} C) \leq d i a m (C)$ ；

vi) $R (s t_{H} C) \leq R (C)$ ；

vii) $r (s t_{H} C) \geq r (C)$ 。

现在叙述Minkowski加法的定义和性质。Minkowski加法和数乘的定义为：

$C + D = {x + y : x \in C, y \in D}$ ,

$λ C = {λ x : x \in C}$ ,

其中 $C, D \in K^{n}$ ， $λ$ 为一个实数。设 $x \in R^{n}$ ，集合 $x + D (= {x + y : y \in D})$ 可以看作D沿向量x的平移，则Minkowski加法的另外一种定义：

$C + D = \underset{x \in C}{\cup} (x + D) = \underset{y \in D}{\cup} (C + y) .$

下面我们列出有关Minkowski加法的性质定理，这些性质将在后文定理的证明中用到。

命题 2.2 [10] 关于集合的Minkowski加法有以下的性质：

i) 若 $C, D \in K^{n}$ ，则 $C + D \in K^{n}$ ；

ii) Minkowski加法作为 $C^{n} \times C^{n}$ 到 $C^{n}$ 的映射是连续的；

iii) 集合 $K^{n}$ 和 $C^{n}$ 关于Minkowski加法构成了交换半群，其单位元为{o}；

iv) 集合 $K^{n}$ 满足消去律，即：若 $C, D, K \in K^{n}$ 并且 $C + K = D + K$ ，则有 $C = D$ ；

v) 集合 $K^{n}$ 满足顺序消去律，即：若 $C, D, K \in K^{n}$ 并且 $C + K \subseteq D + K$ ，则有 $C \subseteq D$ ；

vi) 若 $C \in K^{n}$ ， $\forall λ, μ \in R$ 并且 $λ, μ \geq 0$ ，有 $λ C + μ C = (λ + μ) C$ 。

命题 2.3设 $C_{1}, C_{2}, D_{1}, D_{2} \in C^{n}$ ，并且满足 $C_{1} \subseteq C_{2}, D_{1} \subseteq D_{2}$ ，则有 $C_{1} + D_{1} \subseteq C_{2} + D_{2}$ 。

3. 主要结果

设 $C, D \in C^{n}$ ，H为 $R^{n}$ 中给定的超平面，我们定义如下的算子：

$ϕ (C, D) = s t_{H} (C + D),$

则 $ϕ$ 为 $C^{n} \times C^{n}$ 到 $C^{n}$ 的双变量凸体算子。

定理 3.1在 $ϕ (\cdot, \cdot)$ 在 $C^{n} \times C^{n}$ 上是连续的。

证明考虑 $C^{n}$ 中的收敛序列 ${C_{n}}, {D_{n}}$ 。假设当 $n \to \infty$ 时，两个序列分别收敛于C、D，其中 $C, D \in C^{n}$ 。由Minkowski加法的性质，即命题2.2 i)、ii)，我们可以得到当 $n \to \infty$ 时，有 $C_{n} + D_{n} \to C + D$ 。结合Steiner 对称的连续性，即命题2.1 ii)，可得当 $n \to \infty$ 时，有 $s t_{H} (C_{n} + D_{n}) \to s t_{H} (C + D)$ ，定理得证。

从上面的证明中，我们可以知道该双变量凸体算子 $ϕ (\cdot, \cdot) = s t_{H} (\cdot + \cdot)$ 是具有连续性的，此外，我们也可以证明其同时具有单调性，即在 $C^{n} \times C^{n}$ 上是不减的。

定理 3.2设 $C_{1}, C_{2}, D_{1}, D_{2} \in C^{n}$ ，并且满足 $C_{1} \subseteq C_{2}, D_{1} \subseteq D_{2}$ ，则有 $s t_{H} (C_{1} + D_{1}) \subseteq s t_{H} (C_{2} + D_{2})$ 。

证明由于 $C_{1}, C_{2}, D_{1}, D_{2} \in C^{n}$ ，以及 $C_{1} \subseteq C_{2}, D_{1} \subseteq D_{2}$ ，根据Minkowski加法的性质，即命题2.2 i)和命题2.3，我们可以得到 $C_{1} + D_{1}, C_{2} + D_{2} \in C^{n}$ ，并且 $C_{1} + D_{1} \subseteq C_{2} + D_{2}$ 。结合Steiner对称的性质，即命题2.1 iii)，可得：

$s t_{H} (C_{1} + D_{1}) \subseteq s t_{H} (C_{2} + D_{2}),$

即定理得证。

我们要注意该算子不为线性算子，为此我们举出如下例子：

例3.1设 $R^{2}$ 中的两个凸体 $C = {(x, y) \in R^{2} : 0 \leq x \leq 1, 0 \leq y \leq 1 - x}$ ， $D = {(x, y) \in R^{2} : 0 \leq x, y \leq 1}$ ，令 $H = {(x, 0) \in R^{2} : x \in R}$ ，我们可以证明 $s t_{H} (λ C + D) = λ s t_{H} (C + D)$ ( $λ$ 任意常数)不成立。为此我们可以只需证明当 $λ = 2$ 时，该等式不成立。根据Steiner对称和Minkowski加法的定义，可得： $s t_{H} (2 C + D) = {(x, y) \in R^{2} : y_{2} (x) \leq y \leq y_{1} (x), 0 \leq x \leq 3}$ ，其中

$y_{1} (x) = {\begin{cases} \frac{3}{2}, 0 \leq x \leq 1 \\ - \frac{x}{2} + 2, 1 \leq x \leq 3 \end{cases}$ $y_{2} (x) = {\begin{cases} - \frac{3}{2}, 0 \leq x \leq 1 \\ \frac{x}{2} - 2, 1 \leq x \leq 3 \end{cases}$

同样可得 $2 s t_{H} (C + D) = {(x, y) \in R^{2} : {y^{'}}_{2} (x) \leq y \leq {y^{'}}_{1} (x), 0 \leq x \leq 4}$ ，其中

${y^{'}}_{1} (x) = {\begin{cases} 2, 0 \leq x \leq 2 \\ - \frac{x}{2} + 3, 2 < x \leq 4 \end{cases}$ ${y^{'}}_{2} (x) = {\begin{cases} - 2, 0 \leq x \leq 2 \\ \frac{x}{2} - 3, 2 < x \leq 4 \end{cases}$

显然， $s t_{H} (2 C + D) \neq 2 s t_{H} (C + D)$ ，故而等式 $s t_{H} (λ C + D) = λ s t_{H} (C + D)$ ( $λ$ 任意常数)不成立，即该算子不为线性算子。

下面我们用一些几何量来进一步刻画该双变量凸体算子。

定理 3.3 设 $C, D \in C^{n}$ ，则以下命题是成立的：

i) $d i a m (s t_{H} (C + D)) \leq d i a m (C) + d i a m (D)$ ；

ii) $R (s t_{H} (C + D)) \leq R (C) + R (D)$ ；

iii) $r (s t_{H} (C + D)) \geq r (C) + r (D)$ 。

证明

i) 由直径的定义可得：

$\begin{matrix} d i a m (C + D) = \sup {| x_{1} + y_{1} - (x_{2} + y_{2}) | : x_{1}, x_{2} \in C, y_{1}, y_{2} \in D} \\ \leq \sup {| x_{1} - x_{2} | : x_{1}, x_{2} \in C} + \sup {| y_{1} - y_{2} | : y_{1}, y_{2} \in D} \\ = d i a m (C) + d i a m (D), \end{matrix}$

结合Steiner对称的性质，即命题2.1 v)可得：

$d i a m (s t_{H} (C + D)) \leq d i a m (C + D) \leq d i a m (C) + d i a m (D) .$

ii) 由外接圆的定义，我们可设 $x + R (C) B^{n} \supseteq C, y + R (D) B^{n} \supseteq D$ ，其中 $x \in C, y \in D$ 。根据Minkowski 加法的性质，即命题2.3，可得：

$x + y + (R (C) + R (D)) B^{n} \supseteq C + D .$

进而 $R (C) + R (D) \geq R (C + D)$ 。结合Steiner对称的性质，即命题2.1 vi)可得：

$R (s t_{H} (C + D)) \leq R (C + D) \leq R (C) + R (D) .$

iii) 由内切圆的定义，我们可设 $x + r (C)) B^{n} \subseteq C, y + r (D) B^{n} \subseteq D$ ，其中 $x \in C, y \in D$ 。根据Minkowski 加法的性质，即命题2.3，可得：

$x + y + (r (C) + r (D)) B^{n} \subseteq C + D .$

进而 $r (C) + r (D) \leq r (C + D)$ 。结合Steiner对称的性质，即命题2.1 vii)可得：

$r (s t_{H} (C + D)) \geq r (C + D) \geq r (C) + r (D) .$

证毕。

4. 结语

本文在研究Steiner对称性质的基础之上，结合Minkowski加法，得到了一个双变量凸体算子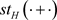，并对其性质展开研究。首先，我们证明了其具有连续性和单调性这样良好的代数性质；其次，我们用直径、内切圆和外接圆这些几何量去刻画该算子，也得到了相应的良好性质。

致谢

本论文是在我导师王拓教授的悉心指导下完成的，从基础知识的学习到论文的选题、参考资料的收集以及论文的修改，每一步都是在王老师的指导下完成的，在此我向我的导师王拓教授表示深切的谢意与祝福。

文章引用

姜亦芳. Steiner对称化下双变量凸体算子st_H(·+·)的性质
The Properties of the Bivariate Convex Body Operator st_H(·+·) under Steiner Symmetrization[J]. 理论数学, 2020, 10(02): 106-110. https://doi.org/10.12677/PM.2020.102017

参考文献

1. Bianchi, G., Gardner, R.J. and Gronchi, P. (2017) Symmetrization in Geometry. Advances in Mathematics, 306, 51-88. https://doi.org/10.1016/j.aim.2016.10.003

2. Gruber, P.M. (2007) Convex and Discrete Geometry. Springer-Verlag, Berlin Heidelberg, 168-187.

3. Klain, D.A. (2011) Steiner Symmetrization Using a Finite Set of Directions. Advances in Applied Mathematics, 48, 340-353. https://doi.org/10.1016/j.aam.2011.09.004

4. Leichtweiss, K. (2008) On Steiner’s Symmetrization of Convex Bodies in Non-Euclidean Geometry. Results in Mathematics, 52, 339-346. https://doi.org/10.1007/s00025-008-0315-3

5. Mcnabb, A. (1967) Partial Steiner Symmetrization and Some Condition Problems. Journal of Mathematical Analysis and Applications, 17, 221-227. https://doi.org/10.1016/0022-247X(67)90147-3

6. Bourgain, J., Lindenstrauss, J. and Milman, V.D. (1989) Estimates Related to Steiner Symmetrizations. Lecture Notes in Mathematics, 1376, 264-273. https://doi.org/10.1007/BFb0090060

7. Chlebík, M., Cianchi, A. and Fusco, N. (2005) The Perimeter Inequality under Steiner Symmetrization: Cases of Equality. Annals of Mathematics, 162, 525-555. https://doi.org/10.4007/annals.2005.162.525

8. 戴进. 凸体的两个几何量在Steiner对称化下的变化及其应用[J]. 数学进展, 2018, 47(5): 767-772.

9. 孙丽英. 凸体的Steiner对称化的两个定理[J]. 理论数学, 2017, 7(5): 368-372.

10. Schneider, R. (2014) Convex Bodies: The Brunn-Minkowski Theory. Cambridge University Press, Cambridge, 139-150.

期刊菜单