Advances in Applied Mathematics
Vol.05 No.03(2016), Article ID:18398,7
pages
10.12677/AAM.2016.53049
Vertex Disjoint Quadrilaterals in Graph
Xiaoning Yi, Jin Yan
School of Mathematics, Shandong University, Jinan Shandong

Received: Jul. 28th, 2016; accepted: Aug. 18th, 2016; published: Aug. 25th, 2016
Copyright © 2016 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



ABSTRACT
Let G be a graph of order n with , where k is a positive integer. Suppose that
, where k is a positive integer. Suppose that , then G contains k independent quadrilaterals.
, then G contains k independent quadrilaterals.
Keywords:Vertex-Disjoint, Cycle, Quadrilaterals

图中点不交的4-圈
衣晓宁,颜谨
山东大学数学学院,山东 济南

收稿日期:2016年7月28日;录用日期:2016年8月18日;发布日期:2016年8月25日

摘 要
令G是一个顶点数为n的图,满足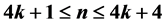 ,k是任意正整数。假设
,k是任意正整数。假设 ,则图G包含k个独立的4-圈。
,则图G包含k个独立的4-圈。
关键词 :点不交,圈,4-圈

1. 引言
本文中的图都为简单图。令 是一个简单图。图
是一个简单图。图 的顶点数和边数分别为
的顶点数和边数分别为 和
和 。图
。图 的一系列子图称为独立的如果任意两个子图在
的一系列子图称为独立的如果任意两个子图在 中没有公共点。令
中没有公共点。令 和
和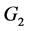 是
是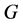 的子图。如果
的子图。如果 和
和 在
在 中没有公共点,我们定义
中没有公共点,我们定义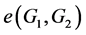 为
为 和
和 之间的边数。令
之间的边数。令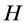 是
是 的子图并且
的子图并且 ,
,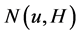 表示
表示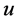 在
在 中的邻点。令
中的邻点。令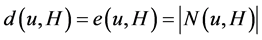 。对
。对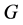 中子图
中子图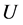 ,令
,令 ,且
,且 表示
表示 的导出子图。
的导出子图。 表示图
表示图 的最小度,同时我们定义
的最小度,同时我们定义
 。
。
我们使用 和
和 表示分别顶点数为
表示分别顶点数为 的圈和路。而且
的圈和路。而且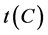 表示圈
表示圈 中弦的个数。对于任意子图
中弦的个数。对于任意子图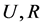 ,我们用符号
,我们用符号 是表示
是表示 是最优的,如果任意
是最优的,如果任意 中子图
中子图 ,
, 满足
满足 。
。 和
和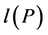 分别表示圈
分别表示圈 和路
和路 的长度,即
的长度,即 和
和 。
。
令 是顶点数为5的包含两个边不交三角形的图,
是顶点数为5的包含两个边不交三角形的图,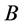 的中心点是度为4的点。令
的中心点是度为4的点。令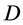 是顶点数为5,由
是顶点数为5,由 删除一条与中心点相连的边获得的图。
删除一条与中心点相连的边获得的图。
图的哈密顿圈问题是图论研究中最著名的问题之一。而图中包含指定长度的圈问题则是哈密顿圈问题的延伸。1963年,Corrádi和Hajnal给出了如下结论。
定理1 [1] 设 是一个顶点为
是一个顶点为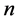 的图。如果
的图。如果 并且
并且 ,那
,那 含有
含有 个点不交的圈。
个点不交的圈。
在2004年,文章 [2] 证明了定理:
定理2 [2] 设 是一个顶点为
是一个顶点为 的图,满足
的图,满足 ,
, 为正整数。假设
为正整数。假设 ,那
,那 含有
含有 个独立的4-圈。
个独立的4-圈。
本文对定理2的度条件加以改进,得到如下命题。
定理3 设 是一个顶点为
是一个顶点为 的图,满足
的图,满足 , 为正整数。假设
, 为正整数。假设 ,那
,那 含有
含有 个独立的4-圈。
个独立的4-圈。
其它相关结果在 [3] - [5] 中有介绍。同时文中其它未见说明的符号请参见 [6] 。
2. 引理
令 是一个顶点数为
是一个顶点数为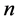 的图,满足
的图,满足 。为了证明,我们先使用如下引理。
。为了证明,我们先使用如下引理。
引理1 [2] 令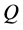 和
和 是图
是图 中两个相互独立的圈,满足
中两个相互独立的圈,满足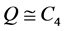 ,
, ,
, 和
和 是最优的。假设
是最优的。假设 ,则存在
,则存在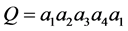 和
和 ,使得
,使得 ,对任意
,对任意 成立
成立 ,
, 。同时,如果
。同时,如果 则
则 。
。
引理2 [2] 令 ,
, 和
和 是图
是图 中三个相互独立的圈,满足
中三个相互独立的圈,满足 ,
,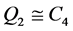 和
和 ,并且使得
,并且使得 是最优的。令
是最优的。令 和
和 ,它们满足
,它们满足 ,对所有
,对所有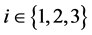 成立
成立 ,并且
,并且 。假设
。假设 不包含
不包含 和
和 。则存在
。则存在 满足
满足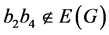 ,
, ,
, 和
和 。
。
引理3 [3] 令 和
和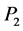 是图
是图 中相互独立的两条路,满足
中相互独立的两条路,满足 和
和 。如果
。如果 ,则
,则 包含一个4-圈。
包含一个4-圈。
引理4 [2] 令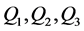 和
和 是图
是图 中四个相互独立的圈,满足
中四个相互独立的圈,满足 ,
, ,并且使得
,并且使得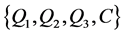 是最优的。令
是最优的。令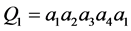 ,
, 和
和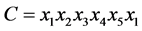 。满足
。满足 ,
, 和
和 ,同时成立
,同时成立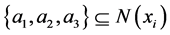 对任意
对任意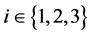 ,
, ,
,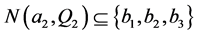 和
和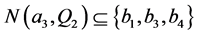 。假设
。假设 不包含
不包含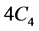 和
和 ,则存在
,则存在 和
和 满足
满足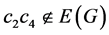 ,
,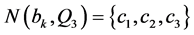 ,
, ,
, 和
和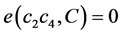 。
。
引理5 [2] 令 和
和 是图
是图 中五个相互独立的圈,满足
中五个相互独立的圈,满足 和
和 ,而且使得
,而且使得 是最优的。令
是最优的。令 ,
, ,
, ,
,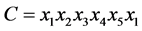 和
和 。假设
。假设 ,
, 和
和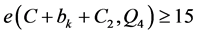 ,满足
,满足 对任意
对任意 ,
, 和
和 ,
, ,
, ,
, ,
,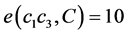 。则
。则 。
。
引理6 [2] 令 和
和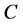 是图
是图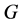 中两个相互独立子图,满足
中两个相互独立子图,满足 和
和 。令
。令 是
是 的中心点。如果
的中心点。如果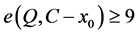 ,则
,则 。
。
引理7 [3] 令 是图
是图 中一个4-圈。令
中一个4-圈。令 和
和 是
是 中两个不相连的点。如果
中两个不相连的点。如果 ,则
,则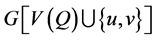 包含一个4-圈
包含一个4-圈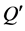 和一条边
和一条边 满足
满足 和
和 是相互独立的,并且
是相互独立的,并且 是与
是与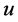 或
或 相连的。
相连的。
引理8 [2] 令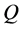 和
和 是图
是图 中两个相互独立的子图,满足
中两个相互独立的子图,满足 和
和 。令
。令 是
是 的中心点。假设
的中心点。假设 ,
, 是最优的,并且
是最优的,并且 不包含
不包含 ,
, 和
和 。则图
。则图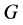 存在
存在 和
和 ,满足
,满足 ,
, ,
, ,
,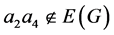 和
和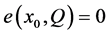 。
。
引理9 [2] 令 和
和 是图
是图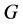 中三个相互独立的子图,满足
中三个相互独立的子图,满足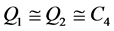 和
和 。令
。令 和
和 ,能够满足
,能够满足 ,
, ,
,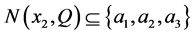 ,
, ,以及
,以及 。假设
。假设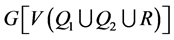 不包含
不包含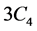 ,
, 和
和 。则存在
。则存在 ,满足
,满足 ,
, ,
, ,和
,和 对某一
对某一 ,并且如果
,并且如果 则
则 ,如果
,如果 则
则 。
。
3. 定理的证明
令 是一个顶点数为
是一个顶点数为 的图,满足
的图,满足 和
和 ,其中
,其中 是一个正整数。假设
是一个正整数。假设 不含
不含 个独立的4-圈。我们假设
个独立的4-圈。我们假设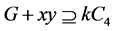 对任意一对不相连的点
对任意一对不相连的点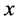 和
和 。令
。令 ,则
,则 。为了证明,我们先证明下列断言。
。为了证明,我们先证明下列断言。
断言1 。
。
证明:假设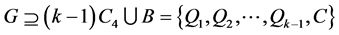 ,满足
,满足 。令
。令 和
和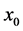 是
是 的中心点。容易看出
的中心点。容易看出 否则
否则 。因为
。因为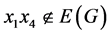 ,
,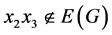 ,则
,则 。这表明存在4-圈
。这表明存在4-圈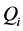 满足
满足 。根据引理6,
。根据引理6, ,矛盾。
,矛盾。
根据图 的选择,
的选择, 包含
包含 个独立4-圈。令
个独立4-圈。令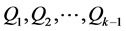 为
为 个4-圈。我们断言
个4-圈。我们断言 。反之,假设
。反之,假设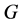 有
有 个独立4-圈
个独立4-圈 ,满足
,满足 含有一条阶为 的路
含有一条阶为 的路 。我们选择
。我们选择 和
和 使得
使得 尽可能大。令
尽可能大。令 ,
, 和
和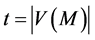 。因此
。因此 。令
。令 满足
满足 。令
。令 。由于
。由于 ,我们可以知道
,我们可以知道 。所以
。所以 。因为
。因为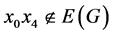 ,则
,则 。这表明存在4-圈
。这表明存在4-圈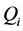 ,不失一般性设
,不失一般性设 ,满足
,满足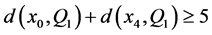 。根据断言2 [2] ,同样可以得到如下结论:
。根据断言2 [2] ,同样可以得到如下结论:
断言2 图 包含
包含 个独立4-圈
个独立4-圈 ,满足
,满足 含有一条阶为5的路。
含有一条阶为5的路。
我们选择 个独立4-圈
个独立4-圈 ,使得
,使得 含有一条阶为5的路。并且在此基础上,令
含有一条阶为5的路。并且在此基础上,令 尽可能大。我们断言
尽可能大。我们断言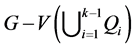 含有一个子图
含有一个子图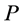 满足
满足 和
和 。假设
。假设 。令
。令 。令
。令 ,
,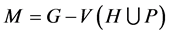 和
和 。则我们有
。则我们有 。因为
。因为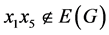 ,则
,则 ,设
,设 。因为
。因为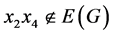 ,
, ,所以
,所以 。根据断言3 [2] ,可以获得如下结论:
。根据断言3 [2] ,可以获得如下结论:
断言3 存在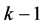 个独立4-圈
个独立4-圈 ,使得
,使得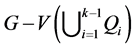 含有一个阶为5,边数至少是5的子图。
含有一个阶为5,边数至少是5的子图。
断言4 。
。
证明:根据断言3,存在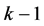 个独立4-圈
个独立4-圈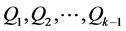 ,使得
,使得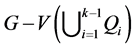 含有一个阶为5,边数至少是5的子图
含有一个阶为5,边数至少是5的子图 。令
。令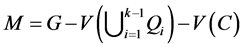 和
和 。如果
。如果 ,令
,令 和
和 是
是 的两个不同端点。则
的两个不同端点。则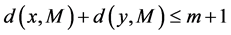 ,否则
,否则 或者
或者 。因为
。因为 ,因此
,因此 。我们可以假设
。我们可以假设 。根据引理7,
。根据引理7, 满足恰有一点
满足恰有一点 和
和 是
是 的端点。因此
的端点。因此 。所以,我们选择
。所以,我们选择 和
和 ,使得
,使得 和
和 尽可能大。
尽可能大。
令 。因为
。因为 不含
不含 和
和 ,我们可知如果
,我们可知如果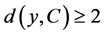 对
对 ,则
,则 。因此
。因此 ,并且因为
,并且因为 和
和 ,所以
,所以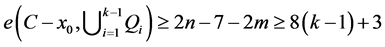 。我们可以假设
。我们可以假设 。根据引理8,令
。根据引理8,令 ,满足
,满足 ,
, ,
, ,和
,和 ,
, 。因此
。因此
 。
。
令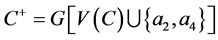 。显然,
。显然, ,否则
,否则 。因此我们看出
。因此我们看出 。所以,
。所以,
 。
。
因为 ,所以
,所以 。如果
。如果 ,则
,则 因为
因为 ,
,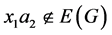 ,
, 。如果
。如果 ,则
,则 因为
因为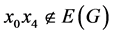 ,
, ,
, 。因此
。因此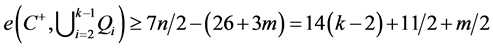 。我们可以假设
。我们可以假设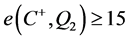 。根据引理9,我们一定有
。根据引理9,我们一定有 ,
, 。令
。令 ,满足
,满足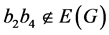 ,
, 。不失一般性,我们假设
。不失一般性,我们假设 和
和 。令
。令 ,
, ,
, 和
和 。显然,
。显然, 和
和 。很容易验证
。很容易验证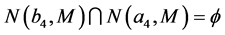 否则
否则 ,
,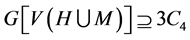 。因此
。因此 和
和 否则
否则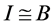 ,
, 的中心点是
的中心点是 。总之,
。总之, 。我们可以假设
。我们可以假设 。根据引理7,设
。根据引理7,设 存在一个点
存在一个点 满足
满足 和
和 ,使得
,使得 。所以
。所以 满足
满足 ,矛盾。断言成立。
,矛盾。断言成立。
断言5 存在 个独立的4-圈
个独立的4-圈 和
和 满足
满足 ,使得
,使得 包含一条顶点数为
包含一条顶点数为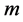 的路。
的路。
证明:根据断言4,我们选择 和
和 使得
使得 包含一条最长的路。在此基础上,令
包含一条最长的路。在此基础上,令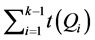 尽可能大。假设
尽可能大。假设 。则
。则 。令
。令 满足如果
满足如果 有一条边是
有一条边是 。因此
。因此 。由于
。由于 ,我们可得
,我们可得 对所有的
对所有的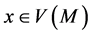 成立。因为
成立。因为 所以
所以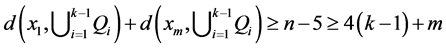 。我们假设
。我们假设 。根据引理7,
。根据引理7, ,因此必然有
,因此必然有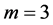 。令
。令 。首先假设
。首先假设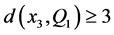 ,不失一般性说
,不失一般性说 。则
。则 因为
因为 。所以
。所以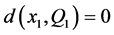 ,矛盾。
,矛盾。
假设 和
和 。令
。令 。则
。则 和
和 ,否则
,否则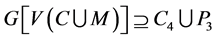 。注意到
。注意到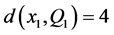 ,我们假设
,我们假设 。可以断言
。可以断言 。否则,则
。否则,则 因为
因为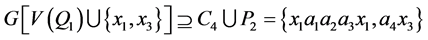 和
和 。这表明
。这表明 和
和 。我们有
。我们有 并且
并且 ,矛盾。因此
,矛盾。因此 。由于
。由于 ,我们看出
,我们看出 。这很容易看出
。这很容易看出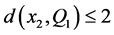 因为
因为 。则
。则 因为
因为 。我们可以假设
。我们可以假设 。令
。令 。相似地,我们可以假设
。相似地,我们可以假设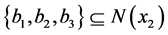 和
和 。所以
。所以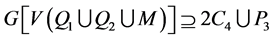 。断言成立。
。断言成立。
根据断言5,令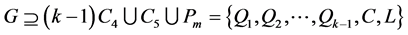 满足
满足 和
和 ,使得
,使得 尽可能大。很容易得到
尽可能大。很容易得到 否则
否则 。令
。令 。我们可以得到
。我们可以得到 因为
因为 ,
, 和
和 。我们假设
。我们假设 。取
。取 。则
。则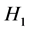 不包含
不包含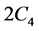 和
和 。令
。令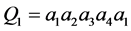 。根据引理1,假设
。根据引理1,假设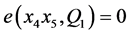 ,
, 对任意
对任意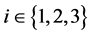 ,并且
,并且 。令
。令 。
。
我们断言存在 满足
满足 。假设断言不成立,显然
。假设断言不成立,显然 。当
。当 ,因为
,因为 ,
, ,则
,则 。我们假设存在
。我们假设存在 满足
满足 。因此我们假设
。因此我们假设 。根据断言6 [2] ,
。根据断言6 [2] , 。令
。令 和
和 。则
。则 。我们可以得到
。我们可以得到 因为
因为 。如果
。如果 ,则
,则 因为
因为 ,
,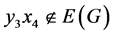 ,
, 。如果
。如果 ,则
,则 因为
因为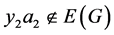 ,
, ,
, 。因此
。因此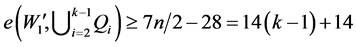 。根据断言6 [2] ,下列断言成立:
。根据断言6 [2] ,下列断言成立:
断言6 存在 满足
满足 。
。
根据断言6,我们假设 。令
。令 。根据引理2,令
。根据引理2,令 满足
满足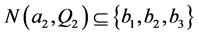 ,
,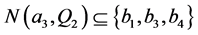 ,
, 和
和 。再令
。再令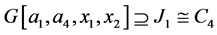 ,
, ,
,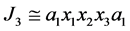 ,并且
,并且 对
对 。
。
取 。根据
。根据 ,我们假设
,我们假设 ,同时令
,同时令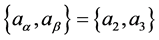 和
和 ,满足
,满足 和
和 对某一
对某一 和
和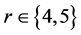 。我们已知
。我们已知 对
对 。如果
。如果 ,则
,则 ,矛盾。则
,矛盾。则 ,因此
,因此 。我们可以得到
。我们可以得到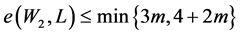 。
。
断言7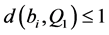 ,
, 对
对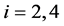 和
和 。
。
证明:首先,假设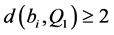 对某一
对某一 。显然可以得到
。显然可以得到 ,矛盾。因此
,矛盾。因此 对任意
对任意 。接下来,假设
。接下来,假设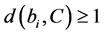 对某一
对某一 。如果
。如果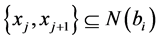 对某一
对某一 ,则
,则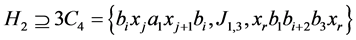 ,矛盾。因此
,矛盾。因此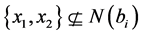 ,同时类似的,
,同时类似的,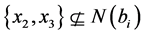 。则
。则 ,并且
,并且 ,矛盾。因此
,矛盾。因此 对任意
对任意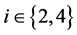 。最后,假设
。最后,假设 。设
。设 对某一
对某一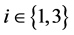 。如果
。如果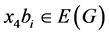 ,令
,令 根据引理3。所以
根据引理3。所以 ,矛盾。因此
,矛盾。因此 。则
。则 因为我们假设
因为我们假设 。这表明
。这表明 ,并且
,并且 对
对 。因此
。因此 ,矛盾。因此断言成立。
,矛盾。因此断言成立。
根据断言7,我们知道 ,
,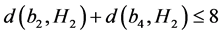 和
和 。由于
。由于 不包含
不包含 ,我们有
,我们有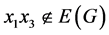 和
和 。如果
。如果 ,则
,则 对
对 ,
, 和
和 。如果
。如果 ,则
,则 对
对 ,
, 和
和 。因此
。因此
 。
。
不失一般性,我们假设 。根据引理4,令
。根据引理4,令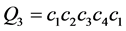 和
和 ,能够满足
,能够满足 ,
, ,
,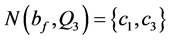 ,
, ,
,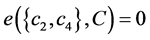 。
。
令 和
和 。由于
。由于 ,我们有
,我们有 。我们可以估计
。我们可以估计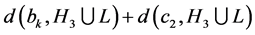 。我们已知
。我们已知 。如果
。如果 ,则
,则 对某一
对某一 。因此
。因此 ,矛盾。因此
,矛盾。因此 和
和 。如果
。如果 对
对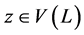 ,则
,则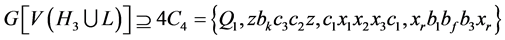 ,矛盾。得到
,矛盾。得到 。所以
。所以 。并且
。并且 。由于
。由于 不包含
不包含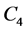 和
和 ,我们有
,我们有 和
和 ,设
,设 。显然,表明
。显然,表明
 。
。
我们可以假设 。根据引理5,
。根据引理5, 。定理证明完毕。
。定理证明完毕。
基金项目
国家自然科学基金资助项目(11271230)。
文章引用
衣晓宁,颜谨. 图中点不交的4-圈
Vertex Disjoint Quadrilaterals in Graph[J]. 应用数学进展, 2016, 05(03): 399-405. http://dx.doi.org/10.12677/AAM.2016.53049
参考文献 (References)
- 1. Corrádi, K. and Hajnal, A. (1963) On the Maximal Number of Independent Circuits in a Graph. Acta Mathematica Academiae Scien-tiarum Hungarica, 14, 423-439. http://dx.doi.org/10.1007/BF01895727
- 2. Wang, H. (2004) Vertex-Disjoint Quadrilaterals in Graphs. Discrete Mathematics, 288, 149-166. http://dx.doi.org/10.1016/j.disc.2004.02.020
- 3. Randerath, B., Schiermeyer, I. and Wang, H. (1999) On Quadrilaterals in a Graph. Discrete Mathematics, 203, 229- 237.
- 4. El-Zahar, M.H. (1984) On Circuits in Graphs. Discrete Mathematics, 50, 227-230. http://dx.doi.org/10.1016/0012-365x(84)90050-5
- 5. Yan, J. and Liu, G.Z. (2003) Quadrilaterals and Paths of Order 4 in Graph. Acts Mathematics Scientific Ser. A, 23, 711- 718.
- 6. Bondy, J.A. and Murty, U.S.R. (1976) Graph Theory with Applications. North-Holland, Amsterdam. http://dx.doi.org/10.1007/978-1-349-03521-2