Advances in Applied Mathematics
Vol.
10
No.
07
(
2021
), Article ID:
43820
,
9
pages
10.12677/AAM.2021.107244
基于马尔科夫随机场对二型糖尿病早期诊断
田雪寒1,王艺舒2*
1青岛大学,山东 青岛
2北京科技大学,北京

收稿日期:2021年6月7日;录用日期:2021年6月28日;发布日期:2021年7月12日

摘要
为了探究二型糖尿病早期动态变化,本文通过分析小鼠标本的组织特异性表达数据,获得相邻时间段之间的差异表达的证据,以表征基因差异表达的动态变化。该数据集中含有丰富的时空信息,但以往的研究中很难充分利用。我们通过在潜在状态上指定马尔可夫随机场(MRF)合并具有时空结构的复杂数据,用蒙特卡洛期望最大化(MCEM)算法计算模型参数,其关键特征是同时考虑基因表达水平的空间相似性和时间依赖性,仿真研究与实例分析结果都表明该方法具有更高的灵敏度,能识别更多的DE基因,能从数据中提取更多生物学上有意义的结果。
关键词
二型糖尿病早期,马尔可夫随机场,MCEM算法

A Markov Random Field-Based Approach for Early Diagnosis of Type 2 Diabetes
Xuehan Tian1, Yishu Wang2*
1Qingdao University, Qingdao Shandong
2University of Science & Technology Beijing, Beijing

Received: Jun. 7th, 2021; accepted: Jun. 28th, 2021; published: Jul. 12th, 2021

ABSTRACT
In order to explore the early dynamic changes of type 2 diabetes mellitus, this paper analyzed the tissue-specific expression data of mouse specimens to obtain the evidence of differential expression between adjacent time periods, so as to characterize the dynamic changes of differential gene expression. This dataset contains abundant spatiotemporal information, but it is difficult to make full use of it in previous studies. We pass in the potential state specified on Markov random field (MRF) combined with space-time structure of complex data, using the Monte Carlo calculation model for the expectation maximization (MCEM) algorithm parameters, its key characteristic is also considering gene expression level of similarity space and time dependence, simulation research and the example analysis results show that this method has higher sensitivity. More DE genes can be identified and more biologically significant results can be extracted from the data.
Keywords:Type 2 Diabetes, Markov Random Field, MCEM Algorithm

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
糖尿病是一种难以根治的慢性疾病,慢性并发症可遍及全身重要器官,急性并发症严重时可危及生命。其中二型糖尿病(T2D)占糖尿病患者总数的九成以上,糖尿病早期由于因胰岛β细胞的代偿机制代偿机制,血糖变化与正常人群差别较小,做专项检查成本高,容易造成医疗资源浪费。因此,诊断出“糖尿病早期”并积极采取干预治疗手段,将有利于推进治愈二型糖尿病这一难题。
自20世纪90年代中后期,基因微阵列技术问世以来便受到科学界的广泛关注,是基因组学中能有效地测量有机体的基因表达水平所使用最广泛的工具。揭示生物网络是系统生物学中的一个关键目标,现在我们能通过微阵列在各种条件下测量基因组水平的表达情况,这些数据可以从统计上推断基因调控网络。在生物学中,许多不同的生物过程都用图表示,比如:包括蛋白质–蛋白质相互作用网络(PPI),转录调控网络和基因共表达网络,生物途径等。
我们用由节点 ,边 组成的图 表示生物网络。对于条件独立图,当且仅当节点i和节点j在给定所有其他节点都不条件独立的情况下, 。高斯图形模型(GGMs)则已经被证明是推断条件独立图的最佳方法之一。高斯图模型是一种概率图模型,GGMs起源于20世纪70年代早期,这一概念源于AP Dempster [1] 的经典论文,是研究基因之间关联网络的工具。在GGM中,
假定p维随机变量 服从多元高斯分布 ,,可以证明 和 的条件独立性等效于 。在GGM中,估计条件独立图等效于估计 中的非零条目。
为了估计GGM,Meinshausen & Buhlmann [2] 证明了使用套索的邻域选择是一个计算吸引力的标准协方差稀疏高维图选择模型。邻域选择分别估计了图中的每个节点的条件独立性限制,因此等价于高斯线性模型的变量选择。同时证明了稀疏的邻域选择方案对于高维图是一致,其一致性取决于惩罚参数的选择。Yuan & Lin [3] 提出了一种有效的算法来扩展Lasso方法的特征选择,并表明这些扩展具有优越的性能,在一定条件下,Lasso变量的选择具有一致性。Friedman et al. [4] 考虑用逆协方差矩阵上的Lasso惩罚来估计稀疏图的问题.,利用Lasso的坐标下降过程,开发了一种简单的图形Lasso算法,命名为图形套索(glasso)。Cai et al. [5],Dobra et al. [6],Wang et al. [7] 等三人同样对估计GGM做出了许多贡献。
本文提出的工作是基于对小鼠标本的组织特异性表达数据的分析所激发的,我们希望通过分析小鼠标本的组织特异性表达数据,在小鼠发育的不同时期,不同的器官组织基因表达动态发育过程不同,为了有效利用该数据集中丰富的时空信息,我们的方法基于马尔可夫随机场(MRF)模型识别相邻时间点的差异表达基因(DE),用蒙特卡洛期望最大化(MCEM)算法计算模型参数,考虑不同时间不同器官组织的病理性变化。我们的方法的关键特征是同时考虑基因表达水平的空间相似性和时间依赖性,获得相邻时间段之间的差异表达的证据,以表征基因差异表达的动态变化,从而探究二型糖尿病早期动态变化。以更好地从数据中提取生物学上有意义的结果。
2. 模型构建
2.1. 差异基因的潜状态模型
对于二型糖尿的早期患者,因胰岛β细胞的代偿机制,血糖波动于正常人群差异很小,通过现有检测方式诊断时患者已经不可能自愈。为了探究二型糖尿病早期动态变化,我们通过分析小鼠标本的组织特异性表达数据,获得相邻时间段之间的差异表达的证据,以表征基因差异表达的动态变化。
首先我们假设 为脂肪,肝脏及胰腺这三处采样组织, 为小鼠发育的第1周、9周、18周三个年龄阶段, 为基因数。令 表示在区域b处,年龄为t的小鼠的重复次数, 为区域b中重复次数的列向量, 为重复次数
我们假设 服从均值为 和方差为 的正态分布 。 为二进制潜状态,表示基因g是否在区域b时刻t中表达,以 为条件,我们假设 遵循高斯分布:
我们假设在特定的区域,混合成分的均值和方差不同,用 表示所有区域的参数向量。 在 条件下的分布具有以下形式:
给定潜变量数组 ,假定 条件独立,则
.
下面我们对于差异表达基因(DE)的分析,我们首先将观察到的数据转换为数组 ,在相邻时段之间执行t检验并将t统计量转换为 。设 和 分别为t-1与t时刻区域b中基因g的表达值的向量,双样本t统计量为:
其中s为 的标准误差的估计值。然后将检验统计量 转换为 :
.
其中 和 是 和 中重复的数目。
基因表达数据由 数组 表示。 表示表示基因g在区域b是否在时段t和t+1之间差异表达的二进制潜状态,这是我们推断的目的。设 为维数 的潜状态数组。在 条件下,我们假设 遵循混合分布:
.
其中 是零密度, 是非零密度。我们假设零密度遵循标准的 分布。我们采用非参数经验贝叶斯框架(Efron [8] ),通过使用R包locfdr将非空密度与自然样条拟合。给定 ,假定条件独立:
.
2.2. MRF模型的先验概率
上述模型和推理目标中的一个关键组成部分是我们未知的潜在状态数组 ,下面我们用MRF模型生成 的先验值 。对于每个基因 ,我们构建一个无向图 ,其中
是节点的集合, 是边的集合, 由 与 组成,
为包含捕获的区域之间空间依赖性的边缘
为包含捕获的相邻周期之间时间依赖性的边缘。
对于 的联合分布概率,我们建立下列成对交互的MRF模型(Besag [9], Lin et al. [10] ):
2-(1)
其中 与 为指标函数,令 ,可得条件概率:
2-(2)
其中 为捕获空间依赖性的参数, 为捕获时间间依赖性的参数。
接下来,我们考虑先验分布 的MRF模型,同时考虑了时间依赖性和空间相似性。我们将3个区域分成两组:用 表示胰腺区域, 非胰腺区域。联合概率类似于2-(1),可以计算条件概率并具有以下形式:
2-(3)
如果 :
如果 :
.
其中 , 为胰腺区之间的空间系数, 为非胰腺区之间的空间系数, 为胰腺区到非胰腺区之间的空间系数, 为非胰腺区到胰腺区之间的空间系数,由对称性可得, 。
3. 参数估计与后验概率估计
3.1. 参数估计
3.1.1. p(X)的参数估计算法
估计MRF参数 和高斯混合模型参数 :
如果给定数组X, ,,可以通过最大似然估计(MLE)进行估计。但是,潜伏状态X是未观察到的,因此也需要进行估计。通常针对缺失数据估计实施期望最大化(EM)算法,但由于期望项难以控制,因此不适用于我们的模型。因此,我们提出以下MCEM算法 [11] 来估计:
1) 通过无偏估计量估计 :
2) 在不考虑空间和时间依赖性的情况下,通过简单的高斯混合模型获得初始估计值
和 。
。
3) 因为没有针对 的显式MLE,所以选择初始估计
的显式MLE,所以选择初始估计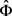 ,将该估计将最大化得到以下伪似然函数
,将该估计将最大化得到以下伪似然函数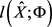 (Besag [12] ):
(Besag [12] ):
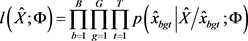
4) 令 ,EM算法中预期的完整数据对数似然可通过蒙特卡罗方法(Wei and Tanner [11] )进行近似:
,EM算法中预期的完整数据对数似然可通过蒙特卡罗方法(Wei and Tanner [11] )进行近似:
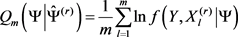 3-(1)
3-(1)
其中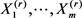 通过吉布斯采样获得。从
通过吉布斯采样获得。从 到,
到, 中的所有条目都被下列公式按顺序更新,
中的所有条目都被下列公式按顺序更新,
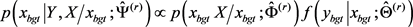 3-(2)
3-(2)
5) 用 更新,使3-(1)最大化:
更新,使3-(1)最大化:

与步骤3相同,我们用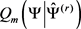 中的伪似然函数替换似然函数。包含
中的伪似然函数替换似然函数。包含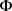 ,
, 的项是可分离的,因此可以分别进行优化。
的项是可分离的,因此可以分别进行优化。
6) 重复步骤4,步骤5,直至收敛。
3.1.2. p(S)的参数估计算法
为了随着时间的推移识别DE基因。在该模型中,只需要迭代地更新MRF先验中的参数 。该算法与上面的算法有一些相似之处:
。该算法与上面的算法有一些相似之处:
1) 汇总Z中的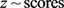 并通过locfdr程序估算
并通过locfdr程序估算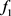 。
。
2) 不考虑空间和时间依赖性的情况下,通过简单的混合模型获得初始估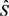 。
。
3) 获得初始估计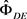 ,其最大化的伪似然函数:
,其最大化的伪似然函数:
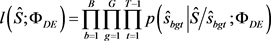
其中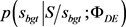 如2-(3)所定义。
如2-(3)所定义。
4) 通过蒙特卡罗近似估计预期的完整数据对数似然:
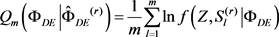 3-(3)
3-(3)
其中 由Gibbs采样获得,从
由Gibbs采样获得,从 到
到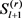 中的所有条目都下列公式被按顺序更新。
中的所有条目都下列公式被按顺序更新。
 3-(4)
3-(4)
5) 通过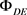 更新
更新 ,直至得到最大化3-(3)。
,直至得到最大化3-(3)。
6) 重复步骤4,步骤5,直至收敛。
3.2. 后验概率估计
为了获得后验概率的估计,我们实现了一个单独的Gibbs采样,并通过MCEM算法估计模型参数。潜在状态根据3-(2)和3-(4)依次更新,关于对DE基因的推断,我们采用基于后验概率的FDR定义(Newton
et al. [13];Li,Wei and Maris [14] )。局部后验f.d.r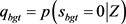 由Gibbs采样估计得来。
由Gibbs采样估计得来。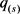 为
为 的升序排序值。让
的升序排序值。让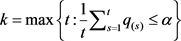 ,然后我们拒绝所有零假设
,然后我们拒绝所有零假设 ,
,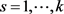 。
。
4. 仿真模拟与实例分析
4.1. 仿真模拟
为了评估我们提出的MRF模型的性能本节进行了仿真模拟。在模拟中通过3轮重复次数生成了在3个区域,3个时间点的500个基因的数据。我们考虑了两种模拟设置模拟的:
模拟设置1:用Gibbs采样器模拟潜状态阵列。采样器从一个可能是EE或DE随机数组开始,在每一轮吉布斯抽样中,每个潜在状态都根据3-(7)顺序更新一次。我们进行了三轮吉布斯抽样,以获得潜在的状态数组S。参数为: ,
,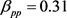 ,
,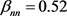 ,
,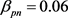 ,
,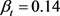 。
。
模拟设置2:在时间点1中,所有基因的死亡概率均为0.1。隐马尔可夫状态随时间模型改变:如果一个基因在t−1时刻为DE,t时刻变成EE概率为0.5;为了保持DE基因的数量不变,我们随机选择相同数量的EE基因在t时刻切换到DE。三层的潜在状态最初设置是相同的。然后随机选择DE状态的不同比例(0.1、0.2、0.5)切换为EE;相同数量的EE状态也切换为DE,以保持DE基因总数不变。
我们在敏感性、特异性和FDR这三个方面比较了这两个模型(见表1)。对于MRF和EB模型,我们选择了 ,满足
,满足 ,控制FDR小于0.05,与EB相比,我们的方法(MRF)了更高的灵敏度。而当相似度降低时,即,从HMM(0.1)到HMM(0.5),FDR在我们的模型中略有增加,但在EB模型中并没有完全增加。
,控制FDR小于0.05,与EB相比,我们的方法(MRF)了更高的灵敏度。而当相似度降低时,即,从HMM(0.1)到HMM(0.5),FDR在我们的模型中略有增加,但在EB模型中并没有完全增加。
Table 1. Comparison between MRF model and EB model
表1. MRF与EB的比较
4.2. 实例分析
本文数据来自小鼠标本的组织特异性表达数据数据集,编号为GSE77943。
我们应用MRF模型来识别相邻时期之间的DE基因。运行20次MCEM算法的迭代,Gibbs采样器的设置为500/1500,估计的MRF参数为 ,
,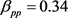 ,
,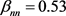 ,
,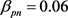 ,
,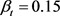 。胰腺与非胰腺区域系数
。胰腺与非胰腺区域系数 远小于胰腺与胰腺
远小于胰腺与胰腺 和非胰腺与非胰腺系数
和非胰腺与非胰腺系数 ,表明胰腺与非胰腺区域之间的组间差异。当假设没有空间和时间依赖性时,模型简化为简单的经验贝叶斯(EB)模型,基于局部FDR控制程序,MRF和EB模型中的阈值分别为0.46和0.32。在两个模型中被鉴定为DE的基因数量是30,605 (MRF)和13,273 (EB),其中11,149 (84%)重叠。较高的阈值导致在MRF模型中识别为DE的更多基因。
,表明胰腺与非胰腺区域之间的组间差异。当假设没有空间和时间依赖性时,模型简化为简单的经验贝叶斯(EB)模型,基于局部FDR控制程序,MRF和EB模型中的阈值分别为0.46和0.32。在两个模型中被鉴定为DE的基因数量是30,605 (MRF)和13,273 (EB),其中11,149 (84%)重叠。较高的阈值导致在MRF模型中识别为DE的更多基因。
后验概率对超参数的选择敏感,我们通过改变后局部FDR的阈值来计算灵敏度和特异性,我们将本文提出的MRF模型与EB模型进行了比较,该模型假设没有时间和空间依赖性。对于两组分别绘制ROC曲线如图1所示,与EB模型相比,MRF模型AUC面积更大,MRF模型的性能更好,MRF模型从空间相似性中获益更多。
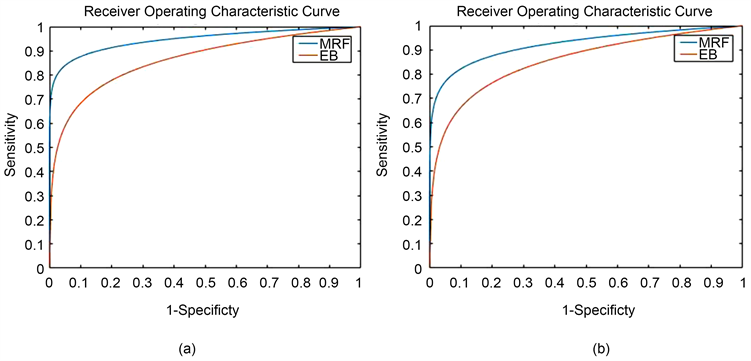
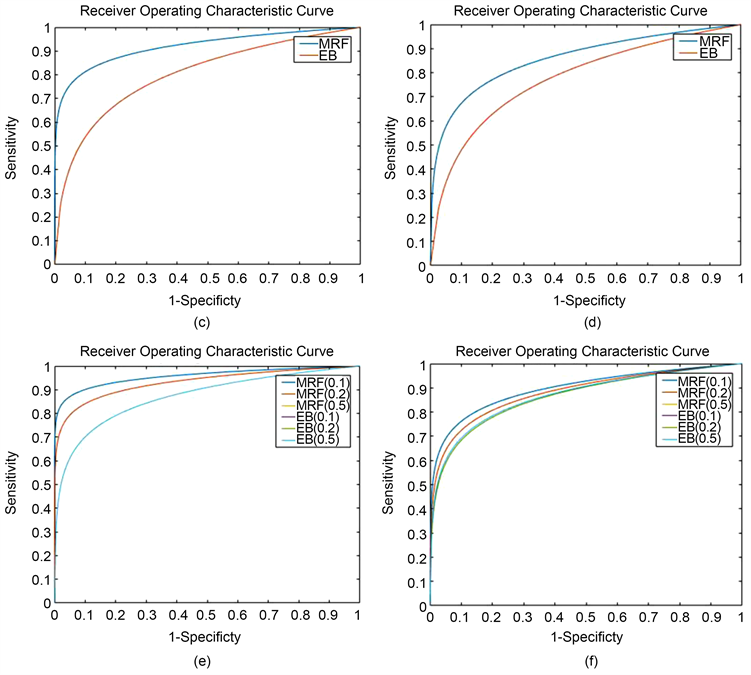
Figure 1. The ROC curve of EB and MRF model
图1. EB与MRF模型的ROC曲线
5. 结论
图形模型在基因表达数据的分析中应用广泛,基于基因表达数据的图形模型可以为可视化基因之间的关系和生成生物假设提供一个有用的工具,我们对图形模型之间的差异很感兴趣。在本文中,我们使用了一种贝叶斯邻域选择程序来估计高斯图形模型,结合了马尔可夫随机场来合并具有时空结构的数据。仿真研究和实例分析表明,将复杂的数据结构合并到联合建模框架中有助于估计,与常用的高斯混合模型相比,该模型具有灵敏度更高,能识别更多的DE基因。
文章引用
田雪寒,王艺舒. 基于马尔科夫随机场对二型糖尿病早期诊断
A Markov Random Field-Based Approach for Early Diagnosis of Type 2 Diabetes[J]. 应用数学进展, 2021, 10(07): 2339-2347. https://doi.org/10.12677/AAM.2021.107244
参考文献
- 1. Dempster, A.P. (1972) Covariance Selection. Biometrics, 28, 157-175. https://doi.org/10.2307/2528966
- 2. Meinshausen, N. and Bühlmann, P. (2006) High-Dimensional Graphs and Variable Selection with the Lasso. Annals of Statistics, 34, 1436-1462. https://doi.org/10.1214/009053606000000281
- 3. Yuan, M. and Lin, Y. (2007) Model Selection and Estimation in the Gaussian Graphical Model. Biometrika, 94, 19-35. https://doi.org/10.1093/biomet/asm018
- 4. Friedman, J., Hastie, T. and Tibshirani, R. (2008) Sparse Inverse Covariance Estimation with the Graphical Lasso. Biostatistics, 9, 432-441. https://doi.org/10.1093/biostatistics/kxm045
- 5. Cai, T., Liu, W. and Luo, X. (2011) A Constrained ℓ1 Minimization Approach to Sparse Precision Matrix Estimation. Journal of the American Statistical Association, 106, 594-607. https://doi.org/10.1198/jasa.2011.tm10155
- 6. Dobra, A., Lenkoski, A. and Rodriguez, A. (2011) Bayesian Inference for General Gaussian Graphical Models with Application to Multivariate Lattice Data. Journal of the American Statistical Association, 106, 1418-1433. https://doi.org/10.1198/jasa.2011.tm10465
- 7. Wang, H. (2012) Bayesian Graphical Lasso Models and Efficient Posterior Computation. Bayesian Analysis, 7, 867-886. https://doi.org/10.1214/12-BA729
- 8. Efron, B. (2004) Large-Scale Simultaneous Hypothesis Testing: The Choice of a Null Hypothesis. Journal of the American Statistical Association, 99, 96-104. https://doi.org/10.1198/016214504000000089
- 9. Besag, J. (1986) On the Statistical Analysis of Dirty Pictures. Journal of the Royal Statistical Society: Series B (Methodological), 48, 259-279. https://doi.org/10.1111/j.2517-6161.1986.tb01412.x
- 10. Lin, Z., Sanders, S.J., Li, M., et al. (2015) A Markov Random Field-Based Approach to Characterizing Human Brain Development Using Spatial-Temporal Transcriptome Data. The Annals of Applied Statistics, 9, 429-451. https://doi.org/10.1214/14-AOAS802
- 11. Wei, G.C.G. and Tanner, M.A. (1990) A Monte Carlo Implementation of the EM Algorithm and the Poor Man’s Data Augmentation Algorithms. Journal of the American Statistical Association, 85, 699-704. https://doi.org/10.1080/01621459.1990.10474930
- 12. Besag, J. (1974) Spatial Interaction and the Statistical Analysis of Lattice Systems. Journal of the Royal Statistical Society: Series B (Methodological), 36, 192-225. https://doi.org/10.1111/j.2517-6161.1974.tb00999.x
- 13. Newton, M.A., Kendziorski, C.M., Richmond, C.S., et al. (2001) On Differential Variability of Expression Ratios: Improving Statistical Inference about Gene Expression Changes from Microarray Data. Journal of Computational Biology, 8, 37-52. https://doi.org/10.1089/106652701300099074
- 14. Li, H., Wei, Z. and Maris, J. (2010) A Hidden Markov Random Field Model for Genome-Wide Association Studies. Biostatistics, 11, 139-150. https://doi.org/10.1093/biostatistics/kxp043
NOTES
*通讯作者。
