具有时滞效应的BAM神经网络的稳定性与分岔 Stability and Bifurcation of BAM Neural Network with Time Delay Effect

doi:10.12677/AAM.2023.126273

Advances in Applied Mathematics
Vol. 12 No. 06 ( 2023 ), Article ID: 67119 , 18 pages
10.12677/AAM.2023.126273

具有时滞效应的BAM神经网络的稳定性与分岔

和光珠

●How to Cite this Article

云南省下关第一中学，云南大理

收稿日期：2023年5月13日；录用日期：2023年6月7日；发布日期：2023年6月15日

摘要

本文研究了一个具有时滞效应的BAM神经网络模型。研究表明当时滞超过一定的临界值时，系统出现Hopf分岔。本文利用规范型理论和中心流形定理得到Hopf分岔的方向和周期解稳定性的条件，并进行了数值模拟，得到了时滞可以诱导BAM神经网络从稳定态转为振荡态的结果，为神经网络的非线性动态特性研究提供了理论依据。

关键词

BAM，神经网络，稳定性，Hopf分岔，时滞

Stability and Bifurcation of BAM Neural Network with Time Delay Effect

Guangzhu He

Xiaguan No. 1 Middle School of Yunnan Province, Dali Yunnan

Received: May 13^th, 2023; accepted: Jun. 7^th, 2023; published: Jun. 15^th, 2023

ABSTRACT

This paper studies a BAM neural network model with time delay effect. Studies show that when the hysteresis exceeds a certain critical value, Hopf bifurcation occurs in the system. In this paper, the direction of Hopf bifurcation and the stability of periodic solution are obtained by using the canonical theory and the central manifold theorem, and the numerical simulation is carried out to obtain the result that time delay can induce the transformation of BAM neural network from a stable state to an oscillating state, which provides a theoretical basis for the study of the nonlinear dynamic characteristics of neural network.

Keywords:BAM, Neural Network, Stability, Hopf Bifurcation, Time Delay

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

通常，神经网络是以电子电路为基础来实现的，而大规模的集成电路中存在中立行为现象(即时滞行为)。近年来，大量专家学者开始关注时滞神经网络的动力学特性(主要包括稳定性、不稳定性、周期性、分岔与混沌等) [1] [2] [3] [4] [5] 。研究时滞神经网络的动力学行为不仅具有重要的理论意义，而且在工程的实际应用中也有重要的指导意义，比如：模式识别、联系记忆、图像处理、组合优化等。

大部分的神经网络只有一种存储或内存模式，而双向联想记忆(BAM)神经网络作为Hopf神经网络单向自联想器的扩展，能够存储多种模式并具有通过正向和反向搜索所需模式的能力 [6] 。因此，BAM神经网络在存储成对的模式或记忆方面有实际的应用，还在模式识别、自动控制等领域都得到了广泛的应用。而对有无时滞的BAM神经网络也进行了广泛的研究 [7] [8] [9] [10] 。

众所周知，神经网络是大规模且复杂的非线性系统，而时滞神经网络的动力学性质更为复杂。大量的周期解是表示网络具有多种记忆模式，因此，Hopf分岔的研究对BAM神经网络的设计和应用具有重要意义。实际上，应用Hopf分岔理论可以使BAM神经网络的不同平衡点产生不同的局部周期解。但对其详尽分析较困难，因此一些作者考虑简化系统的动力学行为。例如，2005和2006年，分别有人研究了具有多个时滞的简化三或四神经元BAM神经网络 [11] [12] ；2009年，Zhang [13] 等人研究了具有时滞和自连接的五神经元BAM神经网络的稳定性和局部Hopf分岔。这些论文，主要考虑的都是由x层的一个神经元和y层的一个神经元组成的系统。然而，还有许多其他形式的BAM神经网络尚未被研究。

2012年，Xu [14] 等人研究了具有两个时滞的六神经元BAM神经网络的稳定性和Hopf分岔的存在性，并给出了保证平衡点稳定性和Hopf分岔存在的充分条件。之后，研究人员又做了进一步的研究，如2015年，Liu [15] 等人研究了具有多时滞的六神经元BAM神经网络的高维分岔问题，解决了BAM神经网络系统的B-T分岔和三重零分岔计算，并展示了不同分岔发生的曲线；2019年，Lin [16] 等人将时间分数阶导数引入到具有时滞的六神经元BAM神经网络系统中，并验证了Hopf分岔的存在性。但是他们都没有给出Hopf分岔的方向和周期解的稳定性的判别。因此，这是一个很有意义并且值得考虑的问题，在此基础上推广模型如下：

${\begin{cases} {\dot{μ}}_{1} (t) = - μ_{1} μ_{1} (t) + c_{21} f_{1} (μ_{2} (t - τ_{2})) + c_{31} f_{1} (μ_{3} (t - τ_{2})) + c_{41} f_{1} (μ_{4} (t - τ_{2})) \\ + c_{51} f_{1} (μ_{5} (t - τ_{2})) + c_{61} f_{1} (μ_{6} (t - τ_{2})), \\ {\dot{μ}}_{2} (t) = - μ_{2} μ_{2} (t) + c_{12} f_{2} (μ_{1} (t - τ_{1})), \\ {\dot{μ}}_{3} (t) = - μ_{3} μ_{3} (t) + c_{13} f_{3} (μ_{1} (t - τ_{1})), \\ {\dot{μ}}_{4} (t) = - μ_{4} μ_{4} (t) + c_{14} f_{4} (μ_{1} (t - τ_{1})), \\ {\dot{μ}}_{5} (t) = - μ_{5} μ_{5} (t) + c_{15} f_{5} (μ_{1} (t - τ_{1})), \\ {\dot{μ}}_{6} (t) = - μ_{6} μ_{6} (t) + c_{16} f_{6} (μ_{1} (t - τ_{1})) . \end{cases}$ (1.1)

其中 $u_{i} (t) (i = 1, 2, 3, 4, 5, 6)$ 表示神经元 $u_{i}$ 在t时刻的状态， $u_{i} (i = 1, 2, 3, 4, 5, 6) > 0$ 为第i个神经元电压与电容比， $c_{i 1}$ 和 $c_{1 i} (i = 1, 2, 3, 4, 5, 6)$ 表示神经元之间的连接权重。从I层到另一J层的时间延迟是 $τ_{1}$ ，而从J层返回到I层的时间延迟是 $τ_{2}$ ，在I层中只有一个神经元，在J层中只有五个神经元。本文以两个延迟之和为参数，当总的时间延迟通过一系列临界值，零解失去其稳定性，发生Hopf分岔。

在本文中，我们做出如下假设：

(H1) $f_{i} \in C^{1}, f_{i} (0) = 0 (i = 1, 2, 3, 4, 5, 6)$ ，且原点 $(0, 0, 0, 0, 0, 0)$ 是系统(1.1)的一个正平衡点。

通过假设，本文重点研究具有时滞效应的六神经元BAM神经网络的局部动力学属性。对比现有的研究成果，首先，从理论上分析了系统(1.1)的局部稳定性和Hopf分岔出现的时滞临界值条件，并给出了Hopf分岔的相应性质。接着，通过本文的研究表明在时滞的调控作用下，系统(1.1)可由渐进稳定态转为振荡态，而现有的研究已经指出要保证神经网络在工程中的作用得到充分应用，首要因素就是保持相应设计的神经网络维持指数稳定或渐进稳定 [17] [18] 。因此，在实际的工程应用当中，需要在稳定状态之前做出时滞调控，从而达到状态转化。最后，本文综合考虑两个时滞带来的影响，简化理论计算的复杂性。虽然在实际应用方面简化了理论，但不影响实际意义的判断与研究。

本文主要分为四个部分。在第2节中，讨论了平衡点的稳定性和Hopf分岔的存在性。在第3节中，利用Hassard在 [19] 中引入的规范型方法和中心流形定理，得到确定Hopf分岔方向和分岔稳定性的判别公式。在第4节中，通过数值模拟来验证前两节中的理论分析结果。最后，对本文的工作进行了总结。

2. 平衡点的稳定性和局部Hopf分岔

在本节中，主要研究平衡点的稳定性和局部Hopf分岔的存在性。

令 $x_{1} (t) = u_{1} (t - τ_{1})$ ， $x_{2} (t) = u_{2} (t)$ ， $x_{3} (t) = u_{3} (t)$ ， $x_{4} (t) = u_{4} (t)$ ， $x_{5} (t) = u_{5} (t)$ ， $x_{6} (t) = u_{6} (t)$ 和 $τ = τ_{1} + τ_{2}$ ，然后我们可以把系统(1.1)改写成如下形式

${\begin{cases} {\dot{x}}_{1} (t) = - μ_{1} x_{1} (t) + c_{21} f_{1} (x_{2} (t - τ)) + c_{31} f_{1} (x_{3} (t - τ)) + c_{41} f_{1} (x_{4} (t - τ)) \\ + c_{51} f_{1} (x_{5} (t - τ)) + c_{61} f_{1} (x_{6} (t - τ)), \\ {\dot{x}}_{2} (t) = - μ_{2} x_{2} (t) + c_{12} f_{2} (x_{1} (t)), \\ {\dot{x}}_{3} (t) = - μ_{3} x_{3} (t) + c_{13} f_{3} (x_{1} (t)), \\ {\dot{x}}_{4} (t) = - μ_{4} x_{4} (t) + c_{14} f_{4} (x_{1} (t)), \\ {\dot{x}}_{5} (t) = - μ_{5} x_{5} (t) + c_{15} f_{5} (x_{1} (t)), \\ {\dot{x}}_{6} (t) = - μ_{6} x_{6} (t) + c_{16} f_{6} (x_{1} (t)) . \end{cases}$ (2.1)

方程(2.1)在 $(0, 0, 0, 0, 0, 0)$ 处的线性化系统为：

${\begin{cases} {\dot{x}}_{1} (t) = - μ_{1} x_{1} (t) + γ_{21} x_{2} (t - τ) + γ_{31} x_{3} (t - τ) + γ_{41} x_{4} (t - τ) \\ + c γ_{51} x_{5} (t - τ) + γ_{61} x_{6} (t - τ), \\ {\dot{x}}_{2} (t) = - μ_{2} x_{2} (t) + γ_{12} x_{1} (t), \\ {\dot{x}}_{3} (t) = - μ_{3} x_{3} (t) + γ_{13} x_{1} (t), \\ {\dot{x}}_{4} (t) = - μ_{4} x_{4} (t) + γ_{14} x_{1} (t), \\ {\dot{x}}_{5} (t) = - μ_{5} x_{5} (t) + γ_{15} x_{1} (t), \\ {\dot{x}}_{6} (t) = - μ_{6} x_{6} (t) + γ_{16} x_{1} (t) . \end{cases}$ (2.2)

这里 $γ_{k 1} = c_{k 1} {f^{'}}_{1} (0) (k = 2, 3, 4, 5, 6)$ ， $γ_{1 m} = c_{1 m} {f^{'}}_{m} (0) (k = 2, 3, 4, 5, 6)$ 。系统(2.2)的特征方程为：

$λ^{6} + a_{1} λ^{5} + b_{1} λ^{4} + c_{1} λ^{3} + d_{1} λ^{2} + e_{1} λ + f_{1} - (a_{2} λ^{4} + b_{2} λ^{3} + c_{2} λ^{2} + d_{2} λ + e_{2}) e^{- λ τ} = 0$ ， (2.3)

其中：

$a_{1} = μ_{1} + μ_{2} + μ_{3} + μ_{4} + μ_{5} + μ_{6}$

$b_{1} = (μ_{1} + μ_{2} + μ_{3} + μ_{4}) (μ_{5} + μ_{6}) + μ_{1} μ_{2} + μ_{3} μ_{4} + μ_{1} μ_{3} + μ_{1} μ_{4} + μ_{2} μ_{3} + μ_{2} μ_{4}$

$\begin{matrix} c_{1} = (μ_{1} + μ_{2} + μ_{3} + μ_{4}) μ_{5} μ_{6} + (μ_{5} + μ_{6}) (μ_{1} μ_{2} + μ_{3} μ_{4} + μ_{1} μ_{3} + μ_{1} μ_{4} + μ_{2} μ_{3} + μ_{2} μ_{4}) \\ + μ_{1} μ_{2} μ_{3} + μ_{1} μ_{2} μ_{4} + μ_{1} μ_{3} μ_{4} + μ_{2} μ_{3} μ_{4} \end{matrix}$

$\begin{matrix} d_{1} = (μ_{1} μ_{2} + μ_{3} μ_{4} + μ_{1} μ_{3} + μ_{1} μ_{4} + μ_{2} μ_{3} + μ_{2} μ_{4}) μ_{5} μ_{6} \\ + (μ_{5} + μ_{6}) (μ_{1} μ_{2} μ_{3} + μ_{1} μ_{2} μ_{4} + μ_{1} μ_{3} μ_{4} + μ_{2} μ_{3} μ_{4}) \end{matrix}$

$e_{1} = μ_{5} μ_{6} (μ_{1} μ_{2} μ_{3} + μ_{1} μ_{2} μ_{4} + μ_{1} μ_{3} μ_{4} + μ_{2} μ_{3} μ_{4}) + (μ_{5} + μ_{6}) μ_{1} μ_{2} μ_{3} μ_{4}$

$f_{1} = μ_{1} μ_{2} μ_{3} μ_{4} μ_{5} μ_{6}$

$a_{2} = γ_{14} + γ_{13} γ_{31} + γ_{12} γ_{21} + γ_{15} γ_{51} + γ_{16} γ_{61}$

$\begin{matrix} b_{2} = γ_{14} (μ_{2} + μ_{3} + μ_{5} + μ_{6}) + γ_{13} γ_{31} (μ_{2} + μ_{4} + μ_{5} + μ_{6}) + γ_{12} γ_{21} (μ_{3} + μ_{4} + μ_{5} + μ_{6}) \\ + γ_{15} γ_{51} (μ_{2} + μ_{3} + μ_{4} + μ_{6}) + γ_{16} γ_{61} (μ_{2} + μ_{3} + μ_{4} + μ_{5}) \end{matrix}$

$\begin{matrix} c_{2} = γ_{14} (μ_{2} μ_{3} + μ_{2} μ_{5} + μ_{2} μ_{6} + μ_{3} μ_{5} + μ_{3} μ_{6} + μ_{5} μ_{6}) \\ + γ_{13} γ_{31} (μ_{2} μ_{4} + μ_{2} μ_{5} + μ_{2} μ_{6} + μ_{4} μ_{5} + μ_{4} μ_{6} + μ_{5} μ_{6}) \\ + γ_{12} γ_{21} (μ_{3} μ_{4} + μ_{3} μ_{5} + μ_{3} μ_{6} + μ_{4} μ_{5} + μ_{4} μ_{6} + μ_{5} μ_{6}) \\ + γ_{15} γ_{51} (μ_{2} μ_{3} + μ_{2} μ_{4} + μ_{2} μ_{6} + μ_{3} μ_{4} + μ_{3} μ_{6} + μ_{4} μ_{6}) \\ + γ_{16} γ_{61} (μ_{2} μ_{3} + μ_{2} μ_{4} + μ_{2} μ_{5} + μ_{3} μ_{4} + μ_{3} μ_{5} + μ_{5} μ_{6}) \end{matrix}$

$\begin{matrix} d_{2} = γ_{14} (μ_{1} μ_{2} μ_{3} + μ_{1} μ_{2} μ_{4} + μ_{1} μ_{3} μ_{4} + μ_{2} μ_{3} μ_{4}) \\ + γ_{13} γ_{31} (μ_{2} μ_{4} μ_{5} + μ_{2} μ_{4} μ_{6} + μ_{2} μ_{5} μ_{6} + μ_{4} μ_{5} μ_{6}) \\ + γ_{12} γ_{21} (μ_{3} μ_{4} μ_{5} + μ_{3} μ_{4} μ_{6} + μ_{3} μ_{5} μ_{6} + μ_{4} μ_{5} μ_{6}) \\ + γ_{15} γ_{51} (μ_{2} μ_{3} μ_{4} + μ_{2} μ_{3} μ_{6} + μ_{2} μ_{4} μ_{6} + μ_{3} μ_{4} μ_{6}) \\ + γ_{16} γ_{61} (μ_{2} μ_{3} μ_{4} + μ_{2} μ_{3} μ_{5} + μ_{2} μ_{4} μ_{5} + μ_{3} μ_{4} μ_{5}) \end{matrix}$

$\begin{matrix} e_{2} = γ_{14} μ_{2} μ_{3} μ_{5} μ_{6} + γ_{13} γ_{31} μ_{2} μ_{4} μ_{5} μ_{6} + γ_{12} γ_{21} μ_{3} μ_{4} μ_{5} μ_{6} \\ + γ_{15} γ_{51} μ_{2} μ_{3} μ_{4} μ_{6} + γ_{16} γ_{61} μ_{2} μ_{3} μ_{4} μ_{5} \end{matrix}$

为了研究方程超越方程(2.3)的根的分布，我们有以下引理：

引理2.1 对于超越方程：

$\begin{matrix} P (λ, e^{- λ τ_{1}}, \dots, e^{- λ τ_{m}}) = λ^{n} + p_{1}^{(0)} λ^{n - 1} + \dots + p_{n - 1}^{(0)} λ + p_{n}^{(0)} \\ + [p_{1}^{(1)} λ^{n - 1} + \dots + p_{n - 1}^{(1)} λ + p_{n}^{(1)}] e^{- λ τ_{1}} + \dots \\ + [p_{1}^{(m)} λ^{n - 1} + \dots + p_{n - 1}^{(m)} λ + p_{n}^{(m)}] e^{- λ τ_{m}} \\ = 0 \end{matrix}$

随着 $(τ = τ_{1}, τ_{2}, τ_{3}, \dots, τ_{m})$ 的变化，在右半开平面内的零点个数的总和 $P (λ, e^{- λ τ_{1}}, \dots, e^{- λ τ_{m}})$ 只有在虚轴水上出现零点时才可能改变。

当 $τ = 0$ 时，方程(2.3)化为：

$λ^{6} + a_{1} λ^{5} + (b_{1} - a_{2}) λ^{4} + (c_{1} - b_{2}) λ^{3} + (d_{1} - c_{2}) λ^{2} + (e_{1} - d_{2}) λ + f_{1} - e_{2} = 0$ (2.4)

使(2.4)式的所有根都有负实部的一组充要条件由著名的Routh-Hurwitz准则给出如下形式：

$D_{1} = a_{1} > 0$ , (2.5)

$D_{2} = \det (\begin{matrix} a_{1} & 1 \\ c_{1} - b_{2} & b_{1} - a_{2} \end{matrix}) = a_{1} (b_{1} - a_{2}) - (c_{1} - b_{2}) > 0$ , (2.6)

$D_{3} = \det (\begin{matrix} a_{1} & 1 & 0 \\ c_{1} - b_{2} & b_{1} - a_{2} & a_{1} \\ e_{1} - d_{2} & d_{1} - c_{2} & c_{1} - b_{2} \end{matrix}) > 0$ , (2.7)

$D_{4} = \det (\begin{matrix} a_{1} & 1 & 0 & 0 \\ c_{1} - b_{2} & b_{1} - a_{2} & a_{1} & 1 \\ e_{1} - d_{2} & d_{1} - c_{2} & c_{1} - b_{2} & b_{1} - a_{2} \\ 0 & f_{1} - e_{2} & e_{1} - d_{2} & d_{1} - c_{2} \end{matrix}) > 0$ , (2.8)

$D_{5} = \det (\begin{matrix} a_{1} & 1 & 0 & 0 & 0 \\ c_{1} - b_{2} & b_{1} - a_{2} & a_{1} & 1 & 0 \\ e_{1} - d_{2} & d_{1} - c_{2} & c_{1} - b_{2} & b_{1} - a_{2} & a_{1} \\ 0 & f_{1} - e_{2} & e_{1} - d_{2} & d_{1} - c_{2} & c_{1} - b_{2} \\ 0 & 0 & 0 & f_{1} - e_{2} & e_{1} - d_{2} \end{matrix}) > 0$ ,(2.9)

$D_{6} = (f_{1} + e_{2}) D_{5} > 0$ . (2.10)

(H2)假设(2.5)~(2.10)成立。

对于 $ω > 0$ ， $i ω$ 为(2.3)的根当且仅当

$\begin{array}{l} - ω^{6} + a_{1} ω^{5} i + b_{1} ω^{4} - c_{1} ω^{3} i - d_{1} ω^{2} + e_{1} ω i + f_{1} \\ - (a_{2} ω^{4} - b_{2} ω^{3} i - c_{2} ω^{2} + d_{2} ω i + e_{2}) (\cos ω τ - i \sin ω τ) = 0 \end{array}$

分离实部和虚部，我们得到

${\begin{cases} (a_{2} ω^{4} - c_{2} ω^{2} + e_{2}) \cos ω τ + (d_{2} ω - b_{2} ω^{3}) \sin ω τ = - ω^{6} + b_{1} ω^{4} - d_{1} ω^{2} + f_{1} \\ (a_{2} ω^{4} - c_{2} ω^{2} + e_{2}) \sin ω τ - (d_{2} ω - b_{2} ω^{3}) \cos ω τ = c_{1} ω^{3} - a_{1} ω^{5} - e_{1} ω \end{cases}$ , (2.11)

因此有

${(a_{2} ω^{4} - c_{2} ω^{2} + e_{2})}^{2} + {(d_{2} ω - b_{2} ω^{3})}^{2} = {(- ω^{6} + b_{1} ω^{4} - d_{1} ω^{2} + f_{1})}^{2} + {(c_{1} ω^{3} - a_{1} ω^{5} - e_{1} ω)}^{2}$ ,

即

$ω^{12} + k_{1} ω^{10} + k_{2} ω^{8} + k_{3} ω^{6} + k_{4} ω^{4} + k_{5} ω^{2} + k_{6} = 0$ , (2.12)

其中

$k_{1} = a_{1}^{2} - 2 b_{1}$ ,

$k_{2} = b_{1}^{2} + 2 d_{1} - 2 a_{1} c_{1} + a_{1}^{2}$ ,

$k_{3} = c_{1}^{2} + 2 a_{1} e_{1} - 2 f_{1} - 2 b_{1} d_{1} + 2 a_{1} c_{1} - b_{2}^{2}$ ,

$k_{4} = d_{1}^{2} + 2 b_{1} f_{1} - 2 c_{1} e_{1} - c_{1}^{2} - 2 a_{1} e_{2} + b_{2} d_{2}$ ,

$k_{5} = e_{1}^{2} - 2 d_{1} f_{1} + 2 c_{1} e_{2} - d_{1}^{2}$ ,

$k_{6} = f_{1}^{2} - e_{2}^{2}$ .

让 $z = ω^{2}$ ，然后(2.12)式变为

$z^{6} + k_{1} z^{5} + k_{2} z^{7} + k_{3} z^{3} + k_{4} z^{2} + k_{5} z + k_{6} = 0$ . (2.13)

定义

$h (z) = z^{6} + k_{1} z^{5} + k_{2} z^{4} + k_{3} z^{3} + k_{4} z^{2} + k_{5} z + k_{6}$ . (2.14)

如果 $μ_{k} (k = 1, 2, 3, 4, 5, 6)$ ， $c_{i 1} (i = 2, 3, 4, 5, 6)$ ， $c_{i j} (i = 2, 3, 4, 5, 6)$ ， $f_{l} (l = 2, 3, 4, 5, 6)$ 由系统(1.1)给出，很容易使用计算机计算出(2.13)的根。由于 $\lim_{z \to + \infty} h (z) = + \infty$ ，可知，如果 $k_{6} < 0$ ，则(2.13)式至少有一个正根。

在不失一般性的前提下，我们假设(2.13)式有6个正根，分别由 $z_{1}$ ， $z_{2}$ ， $z_{3}$ ， $z_{4}$ ， $z_{5}$ ， $z_{6}$ 来定义。那么方程(2.12)有6个正根

$ω_{1} = \sqrt{z_{1}}$ ， $ω_{2} = \sqrt{z_{2}}$ ， $ω_{3} = \sqrt{z_{3}}$ ， $ω_{4} = \sqrt{z_{4}}$ ， $ω_{5} = \sqrt{z_{5}}$ ， $ω_{6} = \sqrt{z_{6}}$ .

由(2.11)式，我们有

$\cos ω_{k} τ = \frac{D}{{(a_{2} ω^{4} - c_{2} ω^{2} + e_{2})}^{2} + {(d_{2} ω - b_{2} ω^{3})}^{2}}$ ,

这里

$D = (- ω^{6} + b_{1} ω^{4} - d_{1} ω^{2} + f_{1}) (a_{2} ω^{4} - c_{2} ω^{2} + e_{2}) - (c_{1} ω^{3} - a_{1} ω^{5} - e_{1} ω) (d_{2} ω - b_{2} ω^{3})$ .

因此，如果我们定义

$τ_{k}^{(j)} = \frac{1}{ω_{k}} {\arccos [\frac{D}{{(a_{2} ω^{4} - c_{2} ω^{2} + e_{2})}^{2} + {(d_{2} ω - b_{2} ω^{3})}^{2}}] + 2 j π}$ , (2.15)

其中 $k = 1, 2, 3, 4, 5, 6$ ； $j = 0, 1, \dots$ ，那么 $\pm i ω_{k}$ 是方程(2.3)对应于 $τ = τ_{k}^{(j)}$ 时的一对纯虚根。定义

$τ_{k} = τ_{k 0}^{(0)} = \min_{k \in {1, 2, 3, 4, 5, 6}} {τ_{k}^{(0)}}$ , $ω_{k} = ω_{k 0}$ . (2.16)

由以上分析可以得出以下结果：

引理2.2 如果(H1)和(H2)成立，那么当 $τ = [0, τ_{0})$ 时(2.3)式所有的根都有负实部而当 $τ = τ_{k}^{(j)}$ ( $k = 1, 2, 3, 4, 5, 6$ ； $j = 0, 1, \dots$ )时(2.3)式有一对纯虚根 $\pm ω_{k}$ 。

设 $λ (τ) = α (τ) + i ω (τ)$ 为(2.3)的根，且 $τ = τ_{0}$ 时满足 $α (τ_{0}) = 0$ ， $ω (τ_{0}) = ω_{0}$ 。由泛函微分方程理论，存在 $ε > 0$ ，使得 $λ (τ)$ 在 $| τ - τ_{0} | < ε$ 时对 $τ$ 是连续可微的。用 $λ (τ)$ 代入(2.3)等式左边，然后两边分别对 $τ$ 求导，我们有

$\begin{array}{l} (6 λ^{5} + 5 a_{1} λ^{4} + 4 b_{1} λ^{3} + 3 c_{1} λ^{2} + 2 d_{1} λ + e_{1}) \frac{d λ}{d τ} \\ - (4 a_{2} λ^{3} + 3 b_{2} λ + 2 c_{2} λ + d_{2}) e^{- λ τ} \frac{d λ}{d τ} \\ + (a_{2} λ^{4} + b_{2} λ^{3} + c_{2} λ^{2} + d_{2} λ + c_{2}) τ e^{- λ τ} \frac{d λ}{d τ} \\ = (a_{2} λ^{4} + b_{2} λ^{3} + c_{2} λ^{2} + d_{2} λ + e_{2}) λ e^{- λ τ} \end{array}$

经计算得

$\begin{matrix} {(\frac{d λ}{d τ})}^{- 1} = \frac{6 λ^{5} + 5 a_{1} λ^{4} + 4 b_{1} λ^{3} + 3 c_{1} λ^{2} + 2 d_{1} λ + e_{1}}{(a_{2} λ^{4} + b_{2} λ^{3} + c_{2} λ^{2} + d_{2} λ + e_{2}) λ e^{- λ τ}} \\ + \frac{(4 a_{2} λ^{3} + 3 b_{2} λ + 2 c_{2} λ + d_{2}) e^{- λ τ}}{(a_{2} λ^{4} + b_{2} λ^{3} + c_{2} λ^{2} + d_{2} λ + e_{2}) λ e^{- λ τ}} - \frac{τ}{λ} \end{matrix}$

结合(2.11)则有

$\begin{matrix} {Re {(\frac{d λ}{d τ})}^{- 1} |}_{λ = i ω_{0}} = - \frac{(5 a_{1} ω_{0}^{4} - 3 c_{1} ω_{0}^{2} + e_{1}) M + (6 ω_{0}^{5} - 4 b_{1} ω_{0}^{3} + 2 d_{1} ω_{0}) N}{M^{2} + N^{2}} \\ + \frac{[(d_{2} - 3 b_{2} ω_{0}^{2}) \cos ω_{0} τ_{0} + (2 c_{2} ω_{0} - 4 a_{2} ω_{0}^{3}) \sin ω_{0} τ_{0}] M}{M^{2} + N^{2}} \\ + \frac{[(2 c_{2} ω_{0} - 4 a_{2} ω_{0}^{3}) \cos ω_{0} τ_{0} - (d_{2} - 3 b_{2} ω_{0}^{2}) \sin ω_{0} τ_{0}] N}{M^{2} + N^{2}} \end{matrix}$

其中 $M = ω_{0}^{2} (c_{1} ω_{0}^{2} - a_{1} ω_{0}^{4} - e_{1})$ ， $N = ω_{0}^{2} (- ω_{0}^{6} + b_{1} ω_{0}^{4} - d_{1} ω^{2} + f_{1})$ 。

为了得到本文的主要结果，我们需要做如下假设：

(H3) (2.14)式至少有一个正实根；

(H4) $Re {(\frac{d λ}{d τ}) |}_{τ = τ_{0}} \neq 0$ 。

由引理2.1和引理2.2，很容易得到以下结论：

定理2.3 如果(H1)~(H4)成立，则系统(1.1)的平衡点 $E_{0} (0, 0, 0, 0, 0, 0)$ 在 $τ = [0, τ_{0})$ 上是渐近稳定的；当 $τ = τ_{0}$ 时，系统(1.1)在平衡点 $E_{0} (0, 0, 0, 0, 0, 0)$ 处经历Hopf分岔。

3. Hopf分岔的方向和稳定性

在本节中，借助Hassard [19] 等人提出的规范型理论和中心流形定理，我们将进一步研究Hopf分岔方向和分岔周期解稳定性。

设从 $[- τ_{0}, 0]$ 到 $R^{6}$ 存在连续映射的Banach空间，配备 $ϕ \in C ([- τ_{0}, 0], R^{6})$ 的上确界范数 $‖ ϕ ‖ = \sup_{- τ_{0} \leq θ \leq 0} | ϕ (θ) |$ 。为简单计，让 $τ = τ_{0} + γ (γ \in R)$ 。然后， $γ = 0$ 是系统(2.1)的分岔值。由时间尺度 $t \to t / τ$ 进行标准化，系统(2.1)可以写成一个在 $C ([- τ_{0}, 0], R^{6})$ 的算子微分方程。那么，我们可以得到：

${\begin{cases} {\dot{x}}_{1} = (γ + τ_{0}) [- μ_{1} x_{1} (t) + \sum_{i = 2}^{6} γ_{1 i} x_{i} (t - 1) + f_{1}] \\ {\dot{x}}_{2} = (γ + τ_{0}) [- μ_{2} x_{2} (t) + γ_{12} x_{1} (t) + f_{2}] \\ {\dot{x}}_{3} = (γ + τ_{0}) [- μ_{3} x_{3} (t) + γ_{13} x_{1} (t) + f_{3}] \\ {\dot{x}}_{4} = (γ + τ_{0}) [- μ_{4} x_{4} (t) + γ_{14} x_{1} (t) + f_{4}] \\ {\dot{x}}_{5} = (γ + τ_{0}) [- μ_{5} x_{5} (t) + γ_{15} x_{1} (t) + f_{5}] \\ {\dot{x}}_{6} = (γ + τ_{0}) [- μ_{6} x_{6} (t) + γ_{16} x_{1} (t) + f_{6}] \end{cases}$ (3.1)

其中

$f_{1} = \frac{1}{2!} {f^{″}}_{1} (0) \sum_{i = 2}^{6} c_{i 1} x_{i}^{2} (t - 1) + \frac{1}{3!} {f^{‴}}_{1} (0) \sum_{i = 2}^{6} c_{i 1} x_{i}^{3} (t - 1) + F_{1 r}$ ,

$f_{2} = \frac{1}{2!} c_{12} {f^{″}}_{2} (0) x_{1}^{2} (t) + \frac{1}{3!} c_{12} {f^{‴}}_{2} (0) x_{1}^{3} (t) + F_{2 r}$ ,

$f_{3} = \frac{1}{2!} c_{13} {f^{″}}_{3} (0) x_{1}^{2} (t) + \frac{1}{3!} c_{13} {f^{‴}}_{3} (0) x_{1}^{3} (t) + F_{3 r}$ ,

$f_{4} = \frac{1}{2!} c_{14} {f^{″}}_{4} (0) x_{1}^{2} (t) + \frac{1}{3!} c_{14} {f^{‴}}_{4} (0) x_{1}^{3} (t) + F_{4 r}$ ,

$f_{5} = \frac{1}{2!} c_{15} {f^{″}}_{5} (0) x_{1}^{2} (t) + \frac{1}{3!} c_{15} {f^{‴}}_{5} (0) x_{1}^{3} (t) + F_{5 r}$ ,

$f_{6} = \frac{1}{2!} c_{16} {f^{″}}_{6} (0) x_{1}^{2} (t) + \frac{1}{3!} c_{16} {f^{‴}}_{6} (0) x_{1}^{3} (t) + F_{6 r}$ .

令 $U = {(u_{1} (t), u_{2} (t), u_{3} (t), u_{4} (t), u_{5} (t), u_{6} (t))}^{T} \in C ([- 1, 0], R^{6})$ ，系统(3.1)可以转化为

$\dot{U} = L_{γ} (U_{t}) + F (γ, U_{t})$ ， (3.2)

然后，分别定义线性算子 $L_{γ} : C \to R^{6}$ 和非线性算子 $F : R \times C \to R^{6}$ 由以下方程表示：

$L_{γ} ϕ = (τ_{0} + γ) [M_{1} ϕ (0) + M_{2} ϕ (- 1)]$ (3.3)

和

$F (γ, ϕ) = (τ_{0} + γ) {(f_{1}, f_{2}, f_{3}, f_{4}, f_{5}, f_{6})}^{T}$ . (3.4)

其中

$M_{1} = (\begin{matrix} - μ_{1} & 0 & 0 & 0 & 0 & 0 \\ γ_{12} & - μ_{2} & 0 & 0 & 0 & 0 \\ γ_{13} & 0 & - μ_{3} & 0 & 0 & 0 \\ γ_{14} & 0 & 0 & - μ_{4} & 0 & 0 \\ γ_{15} & 0 & 0 & 0 & - μ_{5} & 0 \\ γ_{16} & 0 & 0 & 0 & 0 & - μ_{6} \end{matrix})$ , $M_{2} = (\begin{matrix} 0 & γ_{21} & γ_{31} & γ_{41} & γ_{51} & γ_{61} \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{matrix})$

且 $F (γ, ϕ) = (τ_{0} + γ) {\begin{cases} \frac{1}{2!} {f^{″}}_{1} (0) \sum_{i = 2}^{6} c_{i 1} x ϕ_{i}^{2} (- 1) + \frac{1}{3!} {f^{‴}}_{1} (0) \sum_{i = 2}^{6} c_{i 1} ϕ_{i}^{3} (- 1) \\ \frac{1}{2!} c_{12} {f^{″}}_{2} (0) ϕ_{1}^{2} (0) + \frac{1}{3!} c_{12} {f^{‴}}_{2} (0) ϕ_{1}^{3} (0) \\ \frac{1}{2!} c_{13} {f^{″}}_{3} (0) ϕ_{1}^{2} (0) + \frac{1}{3!} c_{13} {f^{‴}}_{3} (0) ϕ_{1}^{3} (0) \\ \frac{1}{2!} c_{14} {f^{″}}_{4} (0) ϕ_{1}^{2} (0) + \frac{1}{3!} c_{14} {f^{‴}}_{4} (0) ϕ_{1}^{3} (0) \\ \frac{1}{2!} c_{15} {f^{″}}_{5} (0) ϕ_{1}^{2} (0) + \frac{1}{3!} c_{15} {f^{‴}}_{5} (0) ϕ_{1}^{3} (0) \\ \frac{1}{2!} c_{16} {f^{″}}_{6} (0) ϕ_{1}^{2} (0) + \frac{1}{3!} c_{16} {f^{‴}}_{6} (0) ϕ_{1}^{3} (0) \end{cases}$ (3.5)

其中 $ϕ = {(ϕ_{1} (θ), ϕ_{2} (θ), ϕ_{3} (θ), ϕ_{4} (θ), ϕ_{5} (θ), ϕ_{6} (θ))}^{T} \in C$ 。由Riesz表示定理可知，存在一个由有界变差函数 $η (θ, γ)$ 构成的6×6矩阵函数如下：

$L_{γ} ϕ = \int_{- 1}^{0} d η (θ, γ) ϕ (θ)$ (3.6)

我们可以选择：

$η (θ, γ) = (τ_{0} + γ) M_{1} δ (θ) + (τ_{0} + γ) M_{2} δ (θ + 1)$ (3.7)

其中 $δ (θ)$ 是狄拉克函数。

对于 $ϕ \in C^{1} ([- 1, 0], R^{6})$ ，定义算子：

$A (γ) ϕ = {\begin{cases} \frac{d ϕ (θ)}{d θ}, θ \in [- τ_{0}, 0), \\ \int_{- 1}^{0} d η (θ, γ) ϕ (θ), θ = 0. \end{cases}$ (3.8)

和 $R (γ) ϕ = {\begin{cases} 0, θ \in [- 1, 0), \\ F (γ, θ), θ = 0. \end{cases}$ (3.9)

为了研究Hopf分岔的特性，我们将系统(3.1)转化为以下这种形式的算子方程：

${\dot{U}}_{t} = A (γ) U_{t} + R (γ) U_{t}$ ， (3.10)

其中 ${\dot{U}}_{t} = U (t + θ)$ 。

对于 $ψ \in C^{1} ([0, 1], R^{6})$ 。A伴随算子为 $A^{*}$ 被定义为：

$A^{*} ψ (θ^{*}) = {\begin{cases} - \frac{d ψ (θ^{*})}{d θ^{*}}, θ^{*} \in [0, 1), \\ \int_{- 1}^{0} d η^{T} (θ^{*}, γ) ψ (- θ^{*}), θ^{*} = 0. \end{cases}$ (3.11)

其中 $η^{T} (θ^{*}, γ)$ 是矩阵 $η (θ^{*}, γ)$ 的转置。

并定义下列双线性内积：

$〈 ψ, ϕ 〉 = \bar{ψ} (0) ϕ (0) - \int_{- 1}^{0} \int_{ξ = 0}^{θ} \bar{ψ} (ξ - θ) d η (θ) ϕ (ξ) d ξ$ , (3.12)

其中 $η (θ) = η (θ, 0)$ 。 $A^{*} (0)$ 和 $A (0)$ 是伴随算子。对应于第2节中的讨论， $\pm i ω_{0}$ 是 $A (0)$ 的特征值并且其他特征值均具有严格的负实部，他们也是 $A^{*} (0)$ 的特征值。接下来，我们将计算对应特征值 $i ω_{0}$ 的特征向量 $q (θ)$ 和对应特征值 $- i ω_{0}$ 的特征向量 $q^{*} (s)$ 。我们可得：

${\begin{cases} A (0) q (0) = i ω_{0} q (θ), \\ A^{*} (0) q^{*} (0) = - i ω_{0} q^{*} (θ^{*}) . \end{cases}$ (3.13)

其中 $θ \in [- 1, 0]$ ， $θ^{*} \in [0, 1]$ 。

定义

$\begin{array}{l} q (θ) = q (0) e^{i ω_{0} τ_{0} θ} = (1, v_{1}, v_{2}, v_{3}, v_{4}, v_{5}) e^{i ω_{0} τ_{0} θ}, \\ q^{*} (s) = q^{*} (0) e^{i ω_{0} τ_{0} s} = G (1, v_{1}^{*}, v_{2}^{*}, v_{3}^{*}, v_{4}^{*}, v_{5}^{*}) e^{i ω_{0} τ_{0} s} \end{array}$ (3.14)

简单计算可有：

$\begin{array}{l} v_{1} = \frac{- i w_{0} γ_{12} + γ_{12} μ_{2}}{w_{0}^{2} + μ_{2}^{2}}, v_{2} = \frac{- i w_{0} γ_{13} + γ_{13} μ_{3}}{w_{0}^{2} + μ_{3}^{2}}, v_{3} = \frac{- i w_{0} γ_{14} + γ_{14} μ_{4}}{w_{0}^{2} + μ_{4}^{2}}, \\ v_{4} = \frac{- i w_{0} γ_{15} + γ_{15} μ_{5}}{w_{0}^{2} + μ_{5}^{2}}, v_{5} = \frac{- i w_{0} γ_{16} + γ_{16} μ_{6}}{w_{0}^{2} + μ_{6}^{2}}, v_{1}^{*} = \frac{{ie}^{i w_{0} τ_{0}} w_{0} γ_{21} + e^{i w_{0} τ_{0}} w_{0} γ_{21} μ_{2}}{w_{0}^{2} + μ_{2}^{2}}, \\ v_{2}^{*} = \frac{{ie}^{i w_{0} τ_{0}} w_{0} γ_{31} + e^{i w_{0} τ_{0}} w_{0} γ_{31} μ_{3}}{w_{0}^{2} + μ_{3}^{2}}, v_{3}^{*} = \frac{{ie}^{i w_{0} τ_{0}} w_{0} γ_{41} + e^{i w_{0} τ_{0}} w_{0} γ_{41} μ_{4}}{w_{0}^{2} + μ_{4}^{2}}, \\ v_{4}^{*} = \frac{{ie}^{i w_{0} τ_{0}} w_{0} γ_{51} + e^{i w_{0} τ_{0}} w_{0} γ_{51} μ_{5}}{w_{0}^{2} + μ_{5}^{2}}, v_{5}^{*} = \frac{{ie}^{i w_{0} τ_{0}} w_{0} γ_{61} + e^{i w_{0} τ_{0}} w_{0} γ_{61} μ_{6}}{w_{0}^{2} + μ_{6}^{2}} \end{array}$

而q和 $q^{*}$ 的归一化条件为

$〈 q^{*}, q = 1 〉, 〈 q^{*}, \bar{q} 〉 = 0$ (3.15)

为了保证 $〈 q^{*}, q 〉 = 1$ ，我们需要通过(3.12)的双线性内积的定义来确定G的值。将(3.14)代入(3.15)中的第一个方程，得到

$\begin{matrix} 〈 q^{*}, q 〉 = {\bar{q}}^{*} (0) q (0) - \int_{- 1}^{0} \int_{ξ = 0}^{θ} {\bar{q}}^{*} (ξ - θ) d η (θ) q (ξ) d ξ \\ = {\bar{q}}^{*} (0) q (0) - \int_{- 1}^{0} \int_{ξ = 0}^{θ} \bar{G} (1, v_{1}^{*}, v_{2}^{*}, v_{3}^{*}, v_{4}^{*}, v_{5}^{*}) e^{- i ω_{0} τ_{0} (ξ - θ)} d η (θ) {(1, v_{1}, v_{2}, v_{3}, v_{4}, v_{5})}^{T} e^{i ω_{0} τ_{0} ξ} d ξ \\ = {\bar{q}}^{*} (0) q (0) - \int_{- 1}^{0} θ e^{- i ω_{0} τ_{0} θ} d η (θ) q (0) \\ = {\bar{q}}^{*} (0) q (0) + {\bar{q}}^{*} (0) τ_{0} [\begin{matrix} 0 & γ_{21} & γ_{31} & γ_{41} & γ_{51} & γ_{61} \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}] e^{- i ω_{0} τ_{0} θ} q (0) \\ = \bar{G} [(1 + v_{1} \bar{v_{1}^{*}}, v_{2} \bar{v_{2}^{*}}, v_{3} \bar{v_{3}^{*}}, v_{4} \bar{v_{4}^{*}}, v_{5} \bar{v_{5}^{*}}) + τ_{0} e^{- ω_{0} τ_{0} θ} (γ_{21} v_{1}, γ_{31} v_{2}, γ_{41} v_{3}, γ_{51} v_{4}, γ_{61} v_{5})] \\ = 1 \end{matrix}$ (3.16)

然后我们可以确定：

$\bar{G} = \frac{1}{(1 + v_{1} \bar{v_{1}^{*}}, v_{2} \bar{v_{2}^{*}}, v_{3} \bar{v_{3}^{*}}, v_{4} \bar{v_{4}^{*}}, v_{5} \bar{v_{5}^{*}}) + τ_{0} e^{- ω_{0} τ_{0} θ} (γ_{21} v_{1}, γ_{31} v_{2}, γ_{41} v_{3}, γ_{51} v_{4}, γ_{61} v_{5})}$ (3.17)

使用Hassard [19] 等人相同的方法，我们首先通过定义来计算坐标来以描述在处的中心流形 $Ω_{0}$ ，定义

$z (t) = 〈 q^{*}, x_{t} 〉$ ， (3.18)

和

$W (t, θ) = U_{t} - 2 Re [z (t), q (θ)]$ (3.19)

式中 $U_{t}$ 为(3.10)的解。

在中心流形 $Ω_{0}$ ： $W (t, θ) = W (z (t), \bar{z} (t), θ)$ ，其中

$W (z, \bar{z}, θ) = W_{20} (θ) \frac{z^{2}}{2} + W_{11} (θ) z \bar{z} + W_{02} (θ) \frac{{\bar{z}}^{2}}{2} + \dots$ (3.20)

显然， $z (t)$ 和 $\bar{z} (t)$ 分别是中心流形 $Ω_{0}$ 在 $q^{*}$ 和 ${\bar{q}}^{*}$ 方向上的局部坐标。注意到若 $U_{t} (θ)$ 是实数，则只需求出一个实根。对于(3.10)的解 $U_{t} \in Ω_{0}$ ，由于 $γ = 0$ ，我们可以有：

$\begin{matrix} \dot{z} (t) = 〈 q^{*}, {\dot{U}}_{t} 〉 \\ = 〈 q^{*}, A U_{t} + R U_{t} 〉 \\ = A 〈^{*} q^{*}, U_{t} 〉 + 〈 {\bar{q}}^{*} (0), F (0, U_{t}) 〉 \\ = i ω_{0} τ_{0} z (t) + {\bar{q}}^{*} (0) F_{0} (z, \bar{z}) \end{matrix}$ (3.21)

等价于

$\dot{z} (t) = i ω_{0} τ_{0} z (t) + g (z, \bar{z})$ (3.22)

其中

$g (z, \bar{z}, θ) = {\bar{q}}^{*} (0) F_{0} (z, \bar{z}) = g_{20} (θ) \frac{z^{2}}{2} + g_{11} (θ) z \bar{z} + g_{02} (θ) \frac{{\bar{z}}^{2}}{2} + g_{21} (θ) \frac{z^{2} \bar{z}}{2} + \dots$ (3.23)

此外，由(3.10)和(3.21)可得

$\begin{matrix} \dot{W} = {\dot{U}}_{t} - \dot{z} (t) q (θ) - \dot{\bar{z}} \bar{q} (θ) \\ = A (0) U_{t} + R_{0} U_{t} - [i w_{0} τ_{1}^{0} z (t) + {\bar{q}}^{*} (0) f_{0} (z, \bar{z})] q (θ) \\ - [- i w_{0} τ_{1}^{0} z (t) + q^{*} (0) {\bar{f}}_{0} (z, \bar{z})] \bar{q} (θ) \\ = {\begin{cases} A (0) W - 2 ℜ ({\bar{q}}^{*} (0) f_{0} (z, \bar{z})), θ \in [- 1, 0) \\ A (0) W - 2 ℜ ({\bar{q}}^{*} (0) f_{0} (z, \bar{z})) + f_{0}, θ = 0 \end{cases} \\ = A (0) W + H (z, \bar{z}, θ) \end{matrix}$ (3.24)

其中

$H (z, \bar{z}, θ) = H_{20} (θ) \frac{z^{2}}{2} + H_{11} (θ) z \bar{z} + H_{02} (θ) \frac{{\bar{z}}^{2}}{2} + \dots$ (3.25)

对方程(3.20)，对W中t求导可得

$\dot{W} = W_{2} \dot{z} + W_{2} \dot{\bar{z}}$ (3.26)

将(3.20)和(3.22)代入(3.26)可得

$\dot{W} = (W_{20} z + W_{11} \bar{z} + \dots) (i ω_{0} τ_{0} z + g) + (W_{11} z + W_{02} \bar{z} + \dots) (- i ω_{0} τ_{0} \bar{z} + \bar{g})$ (3.27)

然后将(3.20)和(3.25)代入(3.24)可得

$\dot{W} = (A W_{20} + H W_{20}) \frac{z^{2}}{2} + (A W_{11} + H W_{11}) z \bar{z} + (A W_{02} + H W_{02}) \frac{{\bar{z}}^{2}}{2} + \dots$ (3.28)

比较(3.27)与(3.28)的系数，可以得到

$(A - 2 i ω_{0} τ_{0} I) W_{20} (θ) = - H_{20} (θ)$ ， (3.29)

$A W_{11} (θ) = - H_{11} (θ)$ . (3.30)

根据方程(3.19)，我们获得

$\begin{array}{l} U_{t} (θ) = W (z, \bar{z}, θ) + z q + \bar{z} \bar{q} \\ q (θ) = (1, v_{1}, v_{2}, v_{3}, v_{4}, v_{5}) e^{i ω_{0} τ_{0} θ} \end{array}$

与(3.5)一起满足：

$g (z, \bar{z}) = {\bar{q}}^{*} (0) F_{0} (z, \bar{z}) = {\bar{q}}^{*} (0) F (0, U_{t}) = {\bar{G}}_{τ_{0}} (1, {\bar{v}}^{*}_{1}, {\bar{v}}^{*}_{2}, {\bar{v}}^{*}_{3}, {\bar{v}}^{*}_{4}, {\bar{v}}^{*}_{5})$ (3.31)

按照Wagner [20] 的方法将(3.23)和(3.31)中的系数进行比较，可以有：

$\begin{array}{l} g_{20} = 2 {\bar{G}}_{τ_{0}} (\frac{1}{2} c_{21} e^{- 2 i ω_{0} τ_{0}} {f^{″}}_{1} (0) v_{1}^{2} + \frac{1}{2} c_{12} {f^{″}}_{2} (0) \bar{v_{1}^{*}} + \frac{1}{2} c_{31} e^{- 2 i ω_{0} τ_{0}} {f^{″}}_{1} (0) v_{2}^{2} + \frac{1}{2} c_{13} {f^{″}}_{3} (0) \bar{v_{2}^{*}} + \frac{1}{2} c_{41} e^{- 2 i ω_{0} τ_{0}} {f^{″}}_{1} (0) v_{3}^{2} \\ + \frac{1}{2} c_{14} {f^{″}}_{4} (0) \bar{v_{3}^{*}} + \frac{1}{2} c_{51} e^{- 2 i ω_{0} τ_{0}} {f^{″}}_{1} (0) v_{4}^{2} + \frac{1}{2} c_{15} {f^{″}}_{5} (0) \bar{v_{4}^{*}} + \frac{1}{2} c_{61} e^{- 2 i ω_{0} τ_{0}} {f^{″}}_{1} (0) v_{5}^{2} + \frac{1}{2} c_{16} {f^{″}}_{6} (0) \bar{v_{5}^{*}}) \end{array}$

$\begin{array}{l} g_{11} = {\bar{G}}_{τ_{0}} (c_{21} {f^{″}}_{1} (0) v_{1} {\bar{v}}_{1} + c_{12} {f^{″}}_{2} (0) \bar{v_{1}^{*}} + c_{31} {f^{″}}_{1} (0) v_{2} {\bar{v}}_{2} + c_{13} {f^{″}}_{3} (0) \bar{v_{2}^{*}} + c_{41} e {f^{″}}_{1} (0) v_{3} {\bar{v}}_{3} \\ + c_{14} {f^{″}}_{4} (0) \bar{v_{3}^{*}} + c_{51} {f^{″}}_{1} (0) v_{4} {\bar{v}}_{4} + c_{15} {f^{″}}_{5} (0) \bar{v_{4}^{*}} + c_{61} {f^{″}}_{1} (0) v_{5} {\bar{v}}_{5} + c_{16} {f^{″}}_{6} (0) \bar{v_{5}^{*}}) \end{array}$

$\begin{matrix} g_{02} = 2 {\bar{G}}_{τ_{0}} (\frac{1}{2} c_{21} e^{- 2 i ω_{0} τ_{0}} {f^{″}}_{1} (0) {\bar{v}}^{2}_{2} + \frac{1}{2} c_{12} {f^{″}}_{2} (0) \bar{v_{1}^{*}} + \frac{1}{2} c_{31} e^{2 i ω_{0} τ_{0}} {f^{″}}_{1} (0) {\bar{v}}^{2}_{2} + \frac{1}{2} c_{13} {f^{″}}_{3} (0) \bar{v_{2}^{*}} \\ + \frac{1}{2} c_{41} e^{2 i ω_{0} τ_{0}} {f^{″}}_{1} (0) {\bar{v}}^{2}_{3} + \frac{1}{2} c_{14} {f^{″}}_{4} (0) \bar{v_{3}^{*}} + \frac{1}{2} c_{51} e^{2 i ω_{0} τ_{0}} {f^{″}}_{1} (0) {\bar{v}}^{2}_{4} + \frac{1}{2} c_{15} {f^{″}}_{5} (0) \bar{v_{4}^{*}} \\ + \frac{1}{2} c_{61} e^{2 i ω_{0} τ_{0}} {f^{″}}_{1} (0) {\bar{v}}^{2}_{5} + \frac{1}{2} c_{16} {f^{″}}_{6} (0) \bar{v_{5}^{*}}) \end{matrix}$

$\begin{matrix} g_{21} = 2 {\bar{G}}_{τ_{0}} (\frac{1}{2} c_{21} e^{- i ω_{0} τ_{0}} {f^{‴}}_{1} (0) v_{1}^{2} {\bar{v}}_{1} + \frac{1}{2} c_{12} {f^{‴}}_{2} (0) \bar{v_{1}^{*}} + \frac{1}{2} c_{31} e^{- i ω_{0} τ_{0}} {f^{‴}}_{1} (0) v_{2}^{2} {\bar{v}}_{2} + \frac{1}{2} c_{13} {f^{‴}}_{3} (0) \bar{v_{2}^{*}} \\ + \frac{1}{2} c_{41} e^{- i ω_{0} τ_{0}} {f^{‴}}_{1} (0) v_{3}^{2} {\bar{v}}_{3} + \frac{1}{2} c_{14} {f^{‴}}_{4} (0) \bar{v_{3}^{*}} + \frac{1}{2} c_{51} e^{- i ω_{0} τ_{0}} {f^{‴}}_{1} (0) v_{4}^{2} {\bar{v}}_{4} + \frac{1}{2} c_{15} {f^{‴}}_{5} (0) \bar{v_{4}^{*}} + \frac{1}{2} c_{61} e^{- i ω_{0} τ_{0}} {f^{‴}}_{1} (0) v_{5}^{2} {\bar{v}}_{5} \\ + \frac{1}{2} c_{16} {f^{‴}}_{6} (0) \bar{v_{5}^{*}} + c_{12} {f^{″}}_{2} (0) \bar{v_{1}^{*}} W_{11}^{1} (0) + c_{13} {f^{″}}_{3} (0) \bar{v_{2}^{*}} W_{11}^{1} (0) + c_{14} {f^{″}}_{4} (0) \bar{v_{3}^{*}} W_{11}^{1} (0) + c_{15} {f^{″}}_{5} (0) \bar{v_{4}^{*}} W_{11}^{1} (0) \\ + c_{16} {f^{″}}_{6} (0) \bar{v_{5}^{*}} W_{11}^{1} (0) + c_{21} e^{- i ω_{0} τ_{0}} {f^{″}}_{1} (0) v_{1} W_{11}^{2} (- 1) + c_{31} e^{- i ω_{0} τ_{0}} {f^{″}}_{1} (0) v_{2} W_{11}^{3} (- 1) + c_{41} e^{- i ω_{0} τ_{0}} {f^{″}}_{1} (0) v_{3} W_{11}^{4} ( - 1 ) \end{matrix}$

$\begin{matrix} + c_{51} e^{- i ω_{0} τ_{0}} {f^{″}}_{1} (0) v_{4} W_{11}^{5} (- 1) + c_{61} e^{- i ω_{0} τ_{0}} {f^{″}}_{1} (0) v_{5} W_{11}^{6} (- 1) + \frac{1}{2} c_{12} {f^{″}}_{2} (0) \bar{v_{1}^{*}} W_{20}^{1} (0) + \frac{1}{2} c_{13} {f^{″}}_{3} (0) \bar{v_{2}^{*}} W_{20}^{1} (0) \\ + \frac{1}{2} c_{14} {f^{″}}_{4} (0) \bar{v_{3}^{*}} W_{20}^{1} (0) + \frac{1}{2} c_{15} {f^{″}}_{5} (0) \bar{v_{4}^{*}} W_{20}^{1} (0) + \frac{1}{2} c_{16} {f^{″}}_{6} (0) \bar{v_{5}^{*}} W_{20}^{1} (0) + \frac{1}{2} c_{21} e^{i ω_{0} τ_{0}} {f^{″}}_{1} (0) {\bar{v}}_{1} W_{20}^{2} (- 1) \\ + \frac{1}{2} c_{31} e^{i ω_{0} τ_{0}} {f^{″}}_{1} (0) {\bar{v}}_{3} W_{20}^{3} (- 1) + \frac{1}{2} c_{41} e^{i ω_{0} τ_{0}} {f^{″}}_{1} (0) {\bar{v}}_{3} W_{20}^{4} (- 1) + \frac{1}{2} c_{51} e^{i ω_{0} τ_{0}} {f^{″}}_{1} (0) {\bar{v}}_{4} W_{20}^{5} (- 1) \\ + \frac{1}{2} c_{61} e^{i ω_{0} τ_{0}} {f^{″}}_{1} (0) {\bar{v}}_{5} W_{20}^{6} (- 1)) \end{matrix}$ (3.32)

因为 $W_{20} (θ)$ 和 $W_{11} (θ)$ 在 $g_{12}$ 中未知，我们继续求解 $W_{20} (θ)$ 和 $W_{11} (θ)$ 。

从(3.10)，(3.22)和(3.24)可得

$\begin{matrix} \dot{W} = {\dot{U}}_{t} - \dot{z} (t) q (θ) - \dot{\bar{z}} \bar{q} (θ) \\ = A_{0} U_{t} + R_{0} U_{t} - [i w_{0} τ_{1}^{0} z (t) + {\bar{q}}^{*} (0) f_{0} (z, \bar{z})] q (θ) - [- i w_{0} τ_{1}^{0} z (t) + q^{*} (0) {\bar{f}}_{0} (z, \bar{z})] \bar{q} (θ) \\ = {\begin{cases} A_{0} W - 2 ℜ ({\bar{q}}^{*} (0) f_{0} (z, \bar{z})), θ \in [- 1, 0) \\ A_{0} W - 2 ℜ ({\bar{q}}^{*} (0) f_{0} (z, \bar{z})) + f_{0}, θ = 0 \end{cases} \\ = A_{0} W + H (z, \bar{z}, θ) \end{matrix}$ (3.33)

其中

$H (z, \bar{z}, θ) = H_{20} (θ) \frac{z^{2}}{2} + H_{11} (θ) z \bar{z} + H_{02} (θ) \frac{{\bar{z}}^{2}}{2} + \dots$ (3.34)

由(3.20)式对t求导有：

$\begin{matrix} \dot{W} = W_{2} \dot{z} + W_{2} \dot{\bar{z}} \\ = (W_{20} (θ) z + W_{11} (θ) \bar{z} + \dots) (i ω_{0} τ_{0} z + g (z, \bar{z})) \\ = (W_{11} (θ) z + W_{02} (θ) \bar{z} + \dots) (- i ω_{0} τ_{0} \bar{z} + \bar{g} (z, \bar{z})) \end{matrix}$ (3.35)

将(3.33)代入(3.35)可得：

$\begin{matrix} \dot{W} = A (0) (W_{20} (θ) \frac{z^{2}}{2} + W_{11} (θ) z \bar{z} + W_{02} (θ) \frac{{\bar{z}}^{2}}{2} + \dots) + H_{20} (θ) \frac{z^{2}}{2} + H_{11} (θ) z \bar{z} + H_{02} (θ) \frac{{\bar{z}}^{2}}{2} + \dots \\ = (A (0) W_{20} (θ) + H_{20} (θ)) \frac{z^{2}}{2} + (A (0) W_{11} (θ) + H_{11} (θ)) z \bar{z} + (A (0) W_{02} (θ) + H_{02} (θ)) \frac{{\bar{z}}^{2}}{2} + \dots \end{matrix}$ (3.36)

分别比较(3.35)和(3.36)式中 $z^{2}$ 和 $z \bar{z}$ 的对应系数可得以下方程

$\begin{array}{l} (A (0) - 2 i w_{0} τ_{0} I) W_{20} (θ) = - H_{20} (θ) \\ A (0) W_{11} (θ) = - H_{11} (θ) \end{array}$ (3.37)

其中I是单位矩阵或恒等变换。

从(3.33)可得

$\begin{matrix} H (z, \bar{z}, θ) = - {\bar{q}}^{*} (0) f_{0} q (θ) - {\bar{q}}^{*} (0) \bar{f_{0}} \bar{q} (θ) \\ = - g (z, \bar{z}) q (0) - \bar{g} (z, \bar{z}) \bar{q} (θ) \\ = - (g_{20} \frac{z^{2}}{2} + g_{11} z \bar{z} + g_{02} \frac{{\bar{z}}^{2}}{2} + \dots) q (θ) \\ - ({\bar{g}}_{20} \frac{{\bar{z}}^{2}}{2} + {\bar{g}}_{11} z \bar{z} + g_{02} \frac{{\bar{z}}^{2}}{2} + \dots) \bar{q} (θ) \end{matrix}$ (3.38)

对 $θ \in [- 1, 0)$ 。

比较(3.38)，(3.34) $z^{2}$ 和 $z \bar{z}$ 的对应系数可得

$\begin{array}{l} H_{20} (θ) = - g_{20} q (θ) - {\bar{g}}_{02} \bar{q} (θ) \\ H_{211} (θ) = - g_{11} q (θ) - {\bar{g}}_{11} \bar{q} (θ) \end{array}$ (3.39)

从(3.37)我们可得

$A (0) W_{20} (θ) = 2 i w_{0} τ_{0} W_{20} (θ) - H_{20} (θ)$ .

根据 $A (0)$ 和 $q (θ)$ 的定义并结合(3.39)有

$\begin{array}{l} {\dot{W}}_{20} (θ) = 2 i w_{0} τ_{0} W_{20} (θ) + g_{20} q (0) e^{i w_{0} τ_{0} θ} + {\bar{g}}_{02} \bar{q} (0) e^{- i w_{0} τ_{0} θ} \\ W_{20} (θ) = \frac{i g_{20}}{w_{0} τ_{0}} q (0) e^{i w_{0} τ_{0} θ} + \frac{i {\bar{g}}_{02}}{3 w_{0} τ_{0}} \bar{q} (0) e^{- i w_{0} τ_{0} θ} + N_{1} e^{2i w_{0} τ_{0} θ} \end{array}$ (3.40)

其中 $N_{1} = {(N_{1}^{(1)}, N_{1}^{(2)}, N_{1}^{(3)}, N_{1}^{(4)}, N_{1}^{(5)}, N_{1}^{(6)})}^{T}$ 是常数向量。

同理可得， ${\dot{W}}_{11} (θ)$ ， $W_{11} (θ)$ 如下

$\begin{array}{l} {\dot{W}}_{11} (θ) = g_{11} q (0) e^{i w_{0} τ_{0} θ} + {\bar{g}}_{11} \bar{q} (0) e^{- i w_{0} τ_{0} θ} \\ W_{11} (θ) = \frac{i g_{11}}{w_{0} τ_{0}} q (0) e^{i w_{0} τ_{0} θ} + \frac{i {\bar{g}}_{11}}{w_{0} τ_{0}} \bar{q} (0) e^{- i w_{0} τ_{0} θ} + N_{2} \end{array}$ (3.41)

其中， $N_{2} = {(N_{2}^{(1)}, N_{2}^{(2)}, N_{2}^{(3)}, N_{2}^{(4)}, N_{2}^{(5)}, N_{2}^{(6)})}^{T}$ 也是常数向量。

接下来继续计算 $N_{1}$ 和 $N_{2}$ 。

从(3.37)和 $A (0)$ 的定义又可以导出如下方程：

$\begin{array}{l} \int_{- 1}^{0} d η (0) W_{20} (θ) = 2 i ω_{0} τ_{0} W_{20} (0) - H_{20} (0) \\ \int_{- 1}^{0} d η (0) W_{11} (θ) = H_{11} (0) \end{array}$ (3.42)

其中， $η (θ) = η (0, θ)$ 。

从(3.33)有

$\begin{array}{l} H_{20} (0) = - g_{20} q (0) - {\bar{g}}_{02} \bar{q} (0) \\ + 2 τ_{0} (\begin{matrix} \frac{1}{2} c_{21} {f^{″}}_{1} (0) v_{1}^{2} e^{- 2 i τ_{0} ω_{0}} + \frac{1}{2} c_{31} {f^{″}}_{1} (0) v_{2}^{2} e^{- 2 i τ_{0} ω_{0}} + \frac{1}{2} c_{41} {f^{″}}_{1} (0) v_{3}^{2} e^{- 2 i τ_{0} ω_{0}} + \frac{1}{2} c_{51} {f^{″}}_{1} (0) v_{4}^{2} e^{- 2 i τ_{0} ω_{0}} + \frac{1}{2} c_{61} {f^{″}}_{1} (0) v_{5}^{2} e^{- 2 i τ_{0} ω_{0}} \\ \frac{1}{2} c_{12} {f^{″}}_{2} (0) \\ \frac{1}{2} c_{13} {f^{″}}_{3} (0) \\ \frac{1}{2} c_{14} {f^{″}}_{4} (0) \\ \frac{1}{2} c_{15} {f^{″}}_{5} (0) \\ \frac{1}{2} c_{16} {f^{″}}_{6} (0) \end{matrix}) \end{array}$ (3.43)

$\begin{array}{l} H_{11} (0) = - g_{11} q (0) - {\bar{g}}_{11} \bar{q} (0) \\ + τ_{0} (\begin{matrix} c_{21} {f^{″}}_{1} (0) v_{1} v_{11} + c_{31} {f^{″}}_{1} (0) v_{2} v_{22} + c_{41} {f^{″}}_{1} (0) v_{3} v_{33} + c_{51} {f^{″}}_{1} (0) v_{4} v_{44} + c_{61} {f^{″}}_{1} (0) v_{5} v_{55} \\ c_{12} {f^{″}}_{2} (0) \\ c_{13} f^{″} (0) \\ c_{14} {f^{″}}_{4} (0) \\ c_{15} {f^{″}}_{5} (0) \\ c_{16} {f^{″}}_{6} (0) \end{matrix}) \end{array}$ (3.44)

将(3.40)的第二个式子和(3.43)代入(3.42)的第一个式子，可以得到

$\begin{array}{l} \int_{- 1}^{0} d η (θ) (\frac{i g_{20}}{w_{0} τ_{0}} q (0) e^{i w_{0} τ_{0} θ} + \frac{i {\bar{g}}_{02}}{3 w_{0} τ_{0}} \bar{q} (0) e^{- i w_{0} τ_{0} θ} + N_{1} e^{2 i w_{0} τ_{0} θ}) \\ = 2 i w_{0} τ_{0} (\frac{i g_{20}}{w_{0} τ_{0}} q (0) + \frac{i {\bar{g}}_{02}}{3 w_{0} τ_{0}} \bar{q} (0) + N_{1}) - H_{20} (0) \end{array}$ (3.45)

因为， $i ω_{0} τ_{1}^{0}$ 是 $A_{0}$ 对应于特征向量 $q (0)$ 的特征值，因此，从(3.45)得

$\begin{array}{l} (2 i w_{0} τ_{0} I - \int_{- 1}^{0} e^{2 i w_{0} τ_{0} θ} d η) N_{1} \\ = 2 τ_{0} (\begin{matrix} \frac{1}{2} c_{21} {f^{″}}_{1} (0) v_{1}^{2} e^{- 2 i τ_{0} w_{0}} + \frac{1}{2} c_{31} {f^{″}}_{1} (0) v_{2}^{2} e^{- 2 i τ_{0} w_{0}} + \frac{1}{2} c_{41} {f^{″}}_{1} (0) v_{3}^{2} e^{- 2 i τ_{0} w_{0}} + \frac{1}{2} c_{51} {f^{″}}_{1} (0) v_{4}^{2} e^{- 2 i τ_{0} w_{0}} + \frac{1}{2} c_{61} {f^{″}}_{1} (0) v_{5}^{2} e^{- 2 i τ_{0} w_{0}} \\ \frac{1}{2} c_{12} {f^{″}}_{2} (0) \\ \frac{1}{2} c_{13} {f^{″}}_{3} (0) \\ \frac{1}{2} c_{14} {f^{″}}_{4} (0) \\ \frac{1}{2} c_{15} {f^{″}}_{5} (0) \\ \frac{1}{2} c_{16} {f^{″}}_{6} (0) \end{matrix}) \end{array}$ (3.46)

同理，我们可得

$\int_{- 1}^{0} d η (θ) N_{2} = - τ_{0} (\begin{matrix} c_{21} {f^{″}}_{1} (0) v_{1} v_{11} + c_{31} {f^{″}}_{1} (0) v_{2} v_{22} + c_{41} {f^{″}}_{1} (0) v_{3} v_{33} + c_{51} {f^{″}}_{1} (0) v_{4} v_{44} + c_{61} {f^{″}}_{1} (0) v_{5} v_{55} \\ c_{12} {f^{″}}_{2} (0) \\ c_{13} {f^{″}}_{3} (0) \\ c_{14} {f^{″}}_{4} (0) \\ c_{15} {f^{″}}_{5} (0) \\ c_{16} {f^{″}}_{6} (0) \end{matrix})$ (3.47)

最后，根据 $η (θ)$ 的定义，解出 $N_{1}$ ， $N_{2}$ 和 $g_{12}$ 。除此之外我们可得以下值

$\begin{array}{l} C_{1} (0) = \frac{i}{2 w_{0} τ_{0}} (g_{11} g_{20} - 2 {| g_{11} |}^{2} - \frac{{| g_{02} |}^{2}}{3}) + \frac{g_{21}}{2}, \\ μ_{2} = - \frac{Re {C_{1} (0)}}{Re {λ^{'} (τ_{0})}}, \\ T_{2} = - \frac{Im {C_{1} (0)} + μ_{2} Im {λ^{'} (τ_{0})}}{w_{0} τ_{0}}, \\ β_{2} = 2 Re {C_{1} (0)} . \end{array}$

定理3.1

1) Hopf分岔的方向由 $μ_{2}$ 决定：如果 $μ_{2} > 0$ ( $μ_{2} < 0$ )，那么Hopf分岔是超临界的(次临界的)，且在 $τ > τ_{0}$ ( $τ < τ_{0}$ )时分岔周期解存在；

2) 分岔周期解的稳定性依赖于 $β_{2}$ ，当 $β_{2} < 0$ ( $β_{2} > 0$ )时，中心流形上的分岔周期解是稳定的(不稳定的)；

3) 分岔周期解的周期由 $T_{2}$ 决定：若 $T_{2} > 0$ ( $T_{2} < 0$ )则周期增加(减少)。

4. 数值模拟

首先，我们提供系统(1.1)的一些数值结果，来验证上一节获得的分析预测。考虑以下系统：

${\begin{cases} {\bar{u}}_{1} (t) = - 4 u_{1} (t) + 4 \tanh (u_{2} (t - τ_{2})) + \tanh (u_{3} (t - τ_{2})) + \tanh (u_{4} (t - τ_{2})) \\ + \tanh (u_{5} (t - τ_{2})) + \tanh (u_{6} (t - τ_{2})), \\ {\bar{u}}_{2} (t) = - 4 u_{2} (t) - 2 \tanh (u_{1} (t - τ_{1})), \\ {\bar{u}}_{3} (t) = - 4 u_{3} (t) - 3 \tanh (u_{1} (t - τ_{1})), \\ {\bar{u}}_{4} (t) = - 4 u_{4} (t) - 2 \tanh (u_{1} (t - τ_{1})), \\ {\bar{u}}_{5} (t) = - 4 u_{5} (t) - 3 \tanh (u_{1} (t - τ_{1})), \\ {\bar{u}}_{6} (t) = - 4 u_{6} (t) - 2 \tanh (u_{1} (t - τ_{1})), \end{cases}$ (4.1)

这个系统有唯一的平衡点 $E_{0} (0, 0, 0, 0, 0, 0)$ ，并且满足定理2.3所述的条件。当 $τ = 0$ 时，平衡点 $E_{0} (0, 0, 0, 0, 0, 0)$ 是渐进稳定的。以 $j = 0$ 为例，通过计算得到 $τ_{0} \approx 1.68$ ， $ω_{0} \approx 0.5621$ 。因此，当 $τ < τ_{0}$ 时，平衡点 $E_{0} (0, 0, 0, 0, 0, 0)$ 是稳定的。这里可以通过计算机模拟进行说明(参见图1(a)~(f))。当 $τ$ 通过临界值 $τ_{0}$ 时，平衡点 $E_{0} (0, 0, 0, 0, 0, 0)$ 失去稳定性，发生Hopf分岔，即从平衡点 $E_{0} (0, 0, 0, 0, 0, 0)$ 产生的周期解分支族，如图2(a)~(f)所示。

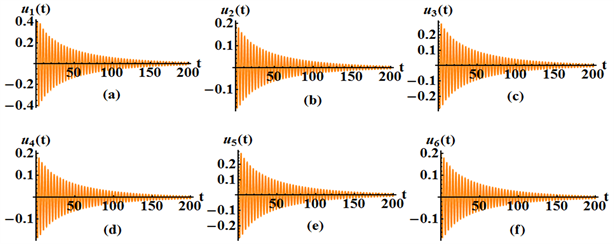
Figure 1. The behavior and phase profile of the system when $τ = 1.5 < τ_{0} \approx 1.68$ . The equilibrium point $E_{0} (0, 0, 0, 0, 0, 0)$ is gradually stable, the initial value is $(0.2, 0.2, 0.2, 0.2, 0.2, 0.2)$

图1. 当 $τ = 1.5 < τ_{0} \approx 1.68$ 时系统的行为和相位画像。平衡点 $E_{0} (0, 0, 0, 0, 0, 0)$ 是渐进稳定的，初始值是 $(0.2, 0.2, 0.2, 0.2, 0.2, 0.2)$

Figure 2. The behavior and phase profile of the system when $τ = 2 > τ_{0} \approx 1.68$ . Hopf bifurcation occurs at equilibrium point $E_{0} (0, 0, 0, 0, 0, 0)$ , the initial value is $(0.2, 0.2, 0.2, 0.2, 0.2, 0.2)$

图2. 当 $τ = 2 > τ_{0} \approx 1.68$ 时系统的行为和相位画像。Hopf分岔发生在平衡点 $E_{0} (0, 0, 0, 0, 0, 0)$ ，初始值是 $(0.2, 0.2, 0.2, 0.2, 0.2, 0.2)$

对于神经网络而言，由于网络的输出是时间的一个函数，对于给定的输入，网络的响应可能是收敛到一个稳定的输出，也可能振荡、无限的增大，或是遵循一种混乱的模式。为了维持系统的稳定性，我们需要控制时滞在临界值之前。要想神经网络在工程中发挥作用，关键是保持所设计的神经网络具有指数稳定性或渐进稳定性。而将神经网络应用于实时计算处理中时，我们通常希望系统有较高的指数收敛度，即神经网络是指数收敛的，稳定性的重要意义不言而喻。

另一方面，可以通过使用定理3.1中的理论分析来获得致使周期振荡分岔的特性，可以计算出以下四个指标值：

$μ_{2} = 19.1617 > 0, T_{2} = 11.4797 > 0, β_{2} = 1.6430 > 0$ (4.2)

根据定理3.1， $μ_{2} > 0$ 表示系统(4.1)经历了超临界Hopf分岔。 $τ > τ_{0}, β_{2} > 0$ 指正平衡点 $E^{*} (0, 0, 0, 0, 0, 0)$ 的分支周期解在中心流形上是不稳定的。另外， $T_{2} > 0$ 表示周期解的周期随着 $τ$ 的增加而增加，这些结果与上述数值分析一致。

5. 论文总结

本文主要分析了时滞对六维BAM系统振荡行为的影响，利用已有的研究方法探索，分别从理论分析和数值模拟两方面获得了一些有意义的成果，为神经网络的推广应用提供了理论依据。

首先，通过研究BAM神经网络相应的线性化系统的特征方程的特征值分布，从理论上得到了系统Hopf分岔产生的临界条件。其次，通过运用规范型方法和中心流形定理，得到了系统在中心流形上的Hopf分岔的规范型。最后，通过数值模拟仿真分析，表明时滞可以诱导BAM神经网络从稳定态转为振荡态(即出现Hopf分岔现象)，进一步验证了主要结果。

虽然研究者对含时滞的BAM神经网络的研究已经取得了一些结果，但是对神经网络丰富动力学行为的认识还很有限。在此篇文章中，我们主要研究含时滞的BAM神经网络模型(1.1)在平衡点的稳定性和Hopf分岔的存在性以及确定Hopf分岔方向和周期解稳定性的条件，研究表明当时滞超过一定的临界值时，系统出现Hopf分岔现象。数值模拟验证了时滞可以诱导BAM神经网络从稳定态转为振荡态的结果，为神经网络的非线性动态特性研究提供了理论依据。文章的主要技术难点在于，一方面，在考虑维数较高方程时，代数方程次数过高会增加计算特征值的难度；另一方面，在研究时滞Hopf分岔问题时，原系统有两个时滞，通过做变量替换，将两时滞的和看为一个量( $τ = τ_{1} + τ_{2}$ )，就可以很容易将两个时滞合并为一个处理，这样可以大大简化理论计算的复杂性。然而，对于系统(1.1)，仍有一些有趣而复杂的动力学行为有待进一步研究。比如，研究高维的分岔问题和讨论复杂连接方式的BAM神经网络系统也是非常有意义的问题，值得进一步考虑。

致谢

感谢审稿人和编辑部提供的有益建议。

文章引用

和光珠. 具有时滞效应的BAM神经网络的稳定性与分岔
Stability and Bifurcation of BAM Neural Network with Time Delay Effect[J]. 应用数学进展, 2023, 12(06): 2718-2735. https://doi.org/10.12677/AAM.2023.126273

参考文献

1. Hopfifield, J.J. (1984) Neurons with Graded Response Have Collective Computional Properties Like Those of Two-State Neurons. Proceedings of the National Academy of Sciences USA, 81, 3088-3092. https://doi.org/10.1073/pnas.81.10.3088

2. Chen, A.P., Huang, L.H. and Cao, J.D. (2003) Existence and Stabil-ity of Almost Periodic Solution for BAM Neural Networks with Delays. Applied Mathematics and Computation, 137, 177-193. https://doi.org/10.1016/S0096-3003(02)00095-4

3. Chen, A.P., Cao, J.D. and Huang, L.H. (2004) Exponential Stability of BAM Neural Networks with Transmission Delays. Neurocomputing, 57, 435-454. https://doi.org/10.1016/j.neucom.2003.10.015

4. Li, Y.K. (2005) Global Exponential Stability of BAM Neural Networks with Delays and Impulses. Chaos, Solitons & Fractals, 24, 279-285. https://doi.org/10.1016/S0960-0779(04)00561-2

5. Huang, X., Cao, J.D. and Huang, D.S. (2007) LMI-Based Approach for Delay-Dependent Exponential Stability Analysis of BAM Neural Networks. Chaos, Solitons & Fractals, 34, 795-812. https://doi.org/10.1016/j.chaos.2006.03.089

6. Kosko, B. (1987) Adaptive Bidirectional Associative Memories. Applied Optics, 26, 4947-4960. https://doi.org/10.1364/AO.26.004947

7. Wang, H., Liao, X.F. and Li, C.D. (2007) Existence and Exponential Stability of Periodic Solution of BAM Neural Networks with Impulse and Time-Varying Delay. Chaos, Solitons & Fractals, 33, 1028-1039. https://doi.org/10.1016/j.chaos.2006.01.112

8. Wang, L. and Zou, X.F. (2004) Hopf Bifurcation in Bidirectional Associative Memory Neural Networks with Delays: Analysis and Computation. Journal of Computational and Applied Mathematics, 167, 73-90. https://doi.org/10.1016/j.cam.2003.09.047

9. Wang, Z.D., Liu,Y.R. and Liu, X.H. (2005) On Global Asymptotic Stability of Neural Networks with Discrete and Distributed Delays. Physics Letters A, 345, 299-308. https://doi.org/10.1016/j.physleta.2005.07.025

10. Zhao, H.Y. (2002) Global Stability of Bidirectional Associative Memory Neural Networks with Distributed Delays. Physics Letters A, 297, 182-190. https://doi.org/10.1016/S0375-9601(02)00434-6

11. Song, Y.L., Han, M.A. and Wei, J.J. (2005) Stability and Hopf Bifurcation Analysis on a Simplified BAM Neural Network with Delays. Physica D: Nonlinear Phenomena, 200, 185-204. https://doi.org/10.1016/j.physd.2004.10.010

12. Yan, X.P. and Li, W.T. (2006) Stability and Bifurcation in a Simplified Four-Neuron BAM Neural Network with Multiple Delays. Discrete Dynamics in Nature and Society, 2006, Article ID: 032529. https://doi.org/10.1155/DDNS/2006/32529

13. Zhang, T.L., Jiang, H.J. and Teng, Z.D. (2009) On the Distribu-tion of the Roots of a Fififth Degree Exponential Polynomial with Application to a Delayed Neural Network Model. Neurocomputing, 72, 1098-1104. https://doi.org/10.1016/j.neucom.2008.03.003

14. Xu, C.J. and Li, P.L. (2012) Bifurcation Analysis in a Simpli-fied Six-Neuron BAM Neural Network with Two Delays. Journal of Information & Computational Science, 9, 3849-3858.

15. Liu, Y.W., Li, S.S., Liu, Z.G. and Wang, R.Q. (2015) High Codimensional Bifurcation Analysis to a Six-Neuron BAM Neural Network. Cognitive Neurodynamics, 10, 149-164. https://doi.org/10.1007/s11571-015-9364-y

16. Lin, J.Z., Xu, R. and Li, L.C. (2019) Effect of Leakage Delay on Hopf Bifurcation in a Fractional BAM Neural Network. International Journal of Bifurcation and Chaos, 29, Article ID: 1950077. https://doi.org/10.1142/S0218127419500779

17. Li, C.D. and Hu, W.F. (2011) Stochastic Stability of Impulsive BAM Neural Networks with Time Delays. Computers & Mathematics with Applications, 61, 2313-2316. https://doi.org/10.1016/j.camwa.2010.09.066

18. Hu, W.F., Li, C.H. and Wu, S.C. (2011) Stochastic Robust Sta-bility for Neutral-Type Impulsive Interval Neural Networks with Distributed Time-Varying Delays. Neural Computing and Applications, 21, 1947-1960. https://doi.org/10.1007/s00521-011-0598-2

19. Hassard, B.D., Kazarinoff, N.D. and Wan, Y. (1981) Theory and Applications of Hopf Bifurcation. Cambridge University Press Archive, Cambridge.

20. Wagner, V.E., Bushnell, D., Passador, L., Brooks, A.I. and Iglewski, B.H. (2003) Microarray Analysis of Pseudomonas aeruginosa Quor-um-Sensing Regulons: Effects of Growth Phase and Environment. Journal of Bacteriology, 185, 2080-2095. https://doi.org/10.1128/JB.185.7.2080-2095.2003

期刊菜单