Advances in Applied Mathematics
Vol.
07
No.
11
(
2018
), Article ID:
27758
,
19
pages
10.12677/AAM.2018.711170
Further Discussion of Dual Orlicz-John Ellipsoids
Tongyi Ma
College of Mathematics and Statistics, Hexi University, Zhangye Gansu
Received: Oct. 29th, 2018; accepted: Nov. 21st, 2018; published: Nov. 28th, 2018

ABSTRACT
As the natural extension of dual Lp-John ellipsoid, Zou and Xiong recently proposed the concept of dual Orlicz John ellipsoid (also call the Orlicz-Legendre ellipsoid), and studied its characteristic properties. This paper uses the totally different methods to restudy the dual Orlicz-John ellipsoid, and proves the existence, uniqueness and characteristic properties of dual Orlicz-John ellipsoid. Meanwhile, we give some interesting properties of dual Orlicz-John ellipsoid and the normalization of dual Orlicz mixed volume, and establish the Orlicz Minkowski inequality of the standardized dual Orlicz mixed volume.
Keywords:Convex Body, John Ellipsoid, Lp-John Ellipsoi, Dual Lp-John Ellipsoid, Dual Orlicz John Ellipsoid
对偶Orlicz-John椭球的再讨论
马统一
河西学院数学与统计学院,甘肃 张掖
收稿日期:2018年10月29日;录用日期:2018年11月21日;发布日期:2018年11月28日

摘 要
作为对偶Lp-John椭球的自然推广,最近Zou和Xiong提出了对偶Orlicz John椭球(也称为Orlicz-Legendre椭球)的概念并研究了它的特征性质。本文运用完全不同的方法重新研究对偶Orlicz John椭球,证明了对偶Orlicz John椭球的存在性、唯一性和特征性质,同时给出了对偶Orlicz John椭球和规范化对偶Orlicz混合体积的一些有趣性质,并建立了规范化的对偶Orlicz混合体积的Orlicz Minkowski不等式。
关键词 :凸体,John椭球,Lp-John椭球,对偶Lp-John椭球,对偶Orlicz John椭球

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
2005年,Lutwak,Yang和Zhang [1] 三人研究小组发表的一篇杰出的文章表明,对于给定的凸体K,存在着一族Lp-John椭球
,使得经典的John椭球JK,Petty椭 [2] [3] 球以及最近发现的对偶Legendre椭球
[4] 都是这一族Lp-John椭球
的特殊情况(
和
)。这种把椭球统一起来的关键点是Lp-John椭球
是给定凸体的Lp-混合体积的极值问题的解 [1]:若K是
中包含原点为其内点的凸体,
,在所有原点对称的椭球E中,满足极值问题
限制于
的解的唯一椭球
称之为Lp-John椭球;在所有原点对称的椭球E中,满足极值问题
限制于
的解的唯一椭球
称之为K的规范化的Lp-John椭球。这里
表示K和E的Lp-混合体积 [5],
表示K的n维体积,
表示欧氏单位球
的n维体积。
另一个经典的结果(其根源来自于力学)可以表述如下:对于
中的凸体K,存在唯一的椭球使得这个椭球在每个方向上的运动惯量与K在相应方向上的运动惯量相同。这个椭球称为K的Legendre椭球
。Legendre椭球是一个很重要的椭球,它与迷向位置的概念以及著名的截面问题紧密相关。
Yu,Leng和Wu [6] 提出了对偶Lp-John椭球
的概念,证明了经典的Löwner椭球
和Legendre椭球
都是对偶Lp-John椭球
的特殊情况(
和
)。这种把椭球统一起来的关键点是对偶Lp-John椭球
是给定凸体的对偶Lp-混合体积的极值问题的解 [6]:若K是
中包含原点为内点的凸体,
,在所有原点对称的椭球E中,满足极值问题
限制于
的解的唯一椭球
称之为K的对偶Lp-John椭球;在所有原点对称的椭球E中,满足极值问题
限制于
的解的唯一椭球
称之为K的规范化的对偶Lp-John椭球。这里
表示K和E的对偶调和Lp-混合体积 [7]。
2010年,在两篇具有里程碑意义的文章 [8] [9] 中,Orlicz Brunn-Minkowski理论浮出了水面,这是Brunn-Minkowski理论的延续和发展。在文章中,Lutwak,Yang和Zhang建立了Orlicz Busemann-Petty质心不等式和Orlicz投影不等式。这个理论是基于Lp-类非对称问题的解决基础之上的,Lp-Brunn-Minkowski理论的非对称问题最早是由Lutwak [5] 提出来的,之后由Ludwig [10],Haberl和Schuster [11] [12] 等人给出了补充和发展。作为Lp-Minkowski问题的延续,偶的Orlicz Minkowski问题也被Haberl [13] 等人解决。虽然Orlicz Brunn-Minkowski理论研究的对象和Brunn-Minkowski理论相比范围扩大了,但我们从Lutwak,Yang和Zhang的工作可以看出,很多基本的性质还是保持了下来,比如仿射等周不等式,这也是我们研究Orlicz Brunn-Minkowski理论的目的所在。可以参考更多文献,如 [4] [14] - [23] 等。
作为Lp-John椭球
和对偶Lp-John椭球
的自然推广,最近,Du和Xiong [24] [25] 提出了Orlicz John椭球和对偶Orlicz John椭球(他们将后者称为Orlicz-Legendre椭球)的概念,并研究了其相应的特征性质,其结果丰富了Orlicz Brunn-Minkowski理论。文 [26] 也独立地研究了Orlicz John椭球。本文中,我们应用完全不同于文 [25] 的方法重新研究对偶Orlicz John椭球,解决其相应极值问题的存在性,唯一性和其特征表示。
事实上,一个凸体K的对偶Orlicz John椭球也是规范化的对偶Orlicz混合体积的相应极值问题的解。受Gruber和Schuster [27] [28] 工作的启发,我们将应用正定二次型的方法来解决与对偶Orlicz John椭球有关的极值问题的存在性、唯一性和其特征表示。这个方法的大致思路如下:对于
中的线性变换,在正交变换下可看成
中的向量,这就把极值问题转化成
中相应的锥的子集上的几何问题。于是对于最小位置问题,我们需要找到有公共切点的光滑的凸子集。这个公共切点就是相应的极值问题的解,使得凸集相切的条件就是解的极值特征。
假设函数
是凸的、严格递增的且
。这种
的集合记为
。我们记
为
中凸体的集合,并记
为包含原点为其内点的凸体的集合。下面关于两个星体的规范化对偶Orlicz混合体积的概念与已有文献 [22] [29] 的定义有所不同。
定义1.1:定义泛函
为
其中
表示
中所有包含原点为其内点的星体的集合,
,且
分别为它们的径向函数。
可以看作是K和L的规范化的对偶Orlicz混合体积。事实上,
是K和L的规范化的对偶调和Lp-混合体积的推广。令
且
,则规范化的对偶调和Lp-混合体积为
对于
,有
值得指出的是,我们这里对
的限制是凸的,也就是说,本文对对偶Lp-John椭球的推广是对于
这个范围内的。
现在,我们考虑如下优化问题。
优化问题:若
以及
。在所有原点对称的椭球中,找到一个椭球E是下面极值问题的解:
限制于
, (
)
这个满足约束条件的最大化问题的椭球E称之为K的
解。其对偶问题是:
限制于
, (
)
这个满足约束条件的最小化问题的椭球E称之为K的
解。
问题
(或
)的解的存在性可由Blaschke选择定理得到保证,我们将在第4节给出证明。
和
的解只差一个标量因子,即下面的引理1.1。
引理1.1:设
。若
是一个关于原点对称的椭球,它是关于K的
的解,则
是一个关于K的
的解。反之,若
是一个关于原点对称的椭球,它是关于K的
的解,则
是一个关于K的
的解。
引理1.1的证明将在第4节给出。进一步,上面最优化问题的解及解的特征可以表述如下:
定理1.1:若
以及
,那么
和
有唯一解,而且椭球E是
(或者
)的解当且仅当它满足
(1)
对于所有
和适当的
。其中
表示E的极体。
因此,解的存在唯一性允许我们提出如下定义。
定义1.2:若
以及
。在所有关于原点对称的椭球E中,满足下列有约束最大化极值问题
限制于
的解的唯一椭球称为K的对偶Orlicz John椭球,且记为
。在所有原点对称的椭球E中,满足下列有约束最小化极值问题
限制于
的解的唯一椭球称为K的规范化的对偶Orlicz John椭球,且记为
。
2. 记号和预备知识
本文在配备了欧氏内积
的
中讨论,记
为其相应的欧氏范数。用
和
分别表示欧氏单位球和单位球面。符号
专指
中原点对称椭球的集合。按惯例,设
表示
中非奇异的线性变换群,
表示
中行列式
的线性变换子群,
表示
中的正交变换群。对于
,记
为T的转置,
为T的转置的逆。如果
,则
为矩阵
,其定义是
对任意
。对于
矩阵
,其内积
定义为
,相应的矩阵范数分别为
和
.
如果
中的凸体K是紧的有非空内部的凸集,则它的支撑函数
被定义为:对于任意的
,
。两个凸体K和L之间的Hausdorff距离
被定义为:
我们记
为
中关于原点的星体的集合。对于
,它的径向函数被定义为:对于任意的
,
。
中的星体K和L称为是膨胀的,如果
的值不依赖于
。从径向函数的定义立即可得:对于紧的星体
,有
(2)
如果
,那么
(3)
显然,如果
,凸体
的径向函数为
(4)
的径向距离
被定义为:
设
,定义实数
和
为
凸体
的Minkowski泛函定义为
。在这种情况下,有
,其中
是K的极集,其定义为:
容易得到
。且凸体的极具有性质:如果
,则
。
给定实数
,对于星体
以及
,Lp-调和径向组合
是一个星体,定义为:
(5)
对偶调和Lp-混合体积由Lutwak引进 [5],其定义为:
(6)
由定义(5)式和(6)式,可以得到下列关于星体K和L的对偶调和Lp-混合体积
的积分表达式 [5] [7]:
(7)
显然,由(7)式可得体积的极坐标公式:
(8)
关于星体K和L的对偶调和Lp-混合体积的Minkowski不等式为:
(9)
等号成立当且仅当K与L互相膨胀。
这一不等式可由Hölder不等式和积分表达式(7)直接得到。特别地,不等式(9)中
的情形是:
(10)
等号成立当且仅当K与L互相膨胀。
3.
的基本性质
由于函数
在
上是严格递增的,那么函数
在
内是严格递减的,且这个函数也是连续的。这样,对于
,
(11)
而且由
的单调性可得,如果
,则
(12)
由于
在
上是严格递增的、凸的且
,那么存在实数
,使得
。
引理3.1:若
,则
证明:令
和
。于是由
的定义和(11)式,可得
以及
又由(2)式可得
以上三式结合,并注意到
在
上单调递增,则得
反之,若
,则
显然成立。
接下来,为了建立
的连续性,我们需要对
进行粗略的上下界估计。
引理3.2:若
以及
,那么
证明:由于
,那么存在实数
,使得
。令
。由(11)式可得
再由
的单调性和体积的极坐标公式(8),得到
这藴含着
另一方面,我们也可得到类似的下界估计:
引理3.2证毕。
若
,由定义1.1和(4)式,我们容易得到
(13)
和
(14)
引理3.3:如果
,那么
和
对于任意
。
假设
,由引理3.2可知
由于
以及
,那么
以及
。结合
的紧性,则存在实数
使得
,对所有的i。
为了证明有界序列
收敛到
,我们只须证明
中任意收敛子列收敛到
。不失一般性,设
的任一收敛子列仍记为
。假设这个子列
。显然,
。令
和
。那么
由(13)式和
,可得
于是,再由(4)式和(11)式,我们得到对所有i,
同时
和
蕰涵着函数
在
上一致收敛。因此,利用
的连续性以及
,可得
结合(11)式,(13)式和(14)式,便得
这就得到了所需要的结果。
下面的引理说明函数
对于
也是连续的。
引理3.4:如果
,那么对于任意
,
证明:令
。由引理3.2给出
由于
,那么
,于是存在实数
使得对所有的i,
。
为了证明有界序列
收敛到
,我们只须证明
中任意收敛子列收敛到
。不失一般性,设
的任一收敛子列仍是
。假设这个子列
。显然,
。因为
,由(11)式可得
结合
以及
,我们得到
即
。于是
。
下面的是
的仿射性质:
引理3.5:如果
以及
,那么
证明:由
的定义和(3)式,我们得到
这就完成了证明。
结合引理3.5,(13)式和(14)式,我们得到对于
,
下面的定理是规范化的对偶Orlicz-Minkowski不等式。
定理3.1:如果
以及
,那么
(15)
等式成立当且仅当K和L是膨胀的。
证明:由于
,那么存在实数
使得
。由(11)式,Jensen 不等式以及L1-对偶调和混合体积的Minkowski不等式(10),我们有
(16)
由
的严格单调性知,上式蕰涵着
等式成立的条件可由Jensen不等式和L1-对偶调和混合体积Minkowski不等式的等号成立的条件得到。如果
是严格凸的,那么Jensen不等式蕰涵着(16)式也是严格的,除非
是常数,也就是说,
对所有的
是个常数,即K和L是膨胀的。如果
不是严格凸的,那么
的严格单调性意味着
必定在一些区间
上是线性的,其它是严格凸的。如果
是线性的,那么(16)式等号自动成立。
结合L1-对偶调和混合体积的Minkowski不等式等号成立的条件,我们得到不等式(15)等号成立当且仅当K和L是膨胀的。定理3.1证毕。
注意到如果
,那么
,不等式(15)就是Lp-对偶调和混合体积Min-kowski不等式(9)。
4. 主要结果的证明
在本节中,我们首先给出引理1.1的证明。
引理1.1的证明:首先证明
中的约束条件可以转化为
,即满足极值问题
的椭球
必须满足
。事实上,设
且
。由(14)式知
。因为
这意味着E不是
的解答。
现在设
且
。由(14)式知
,因此
满足
的约束条件。又因为
是极值问题
的解答,则有
。因此,由假设
,事实
和(14)式,我们有
这说明
是
的解。
反之,设
被
所控制。因为
满足
的约束条件,而
是满足约束条件
的
的解,于是有
因此
,即
这说明
是
的解。证毕。
著名的Blaschke选择定理表明,如果
是一族满足条件
的凸体,其中r和R为两个给定的常数且
,那么
一定有一个收敛到某一凸体K的子列
。
假设X是
中的一个有界集,定义它的通径(diameter)为
其中
表示x和y之间的由欧氏范数诱导出的欧氏距离。
引理4.1:若
,那么
和
的解存在。
证明:设
,则K满足
。则由(2)式知
。设
是一族非退化的原点对称椭球,根据Blaschke选择定理,我们只需证明存在常数
使得
,其中
满足
。根据凸体的通径定义和径向函数的定义,易知对于所有的
,有
设
。由(11)式,
的单调递增性,Jensen不等式以及星体的极坐标体积公式(8),得到
这个不等式意味着
因此,由
的约束条件
,可得
即
另一方面,设
,则
是度量空间
中的紧集。因此存在通用常数
使得对于任意
有
。令
,显然
满足
的约束条件,且
固定
。由引理3.3知
是紧集
上的连续泛函,故存在正数
使得对于任意
有
。由此,并结合上式即得
这里
。
这样,满足
的椭球序列
的通径是一致有界的,因而有下确界,那么
的存在性可由Blaschke选择定理保证。由于
和
的解只差一个有限的标量因子,因此
的解的存在性也能保证。
由于
和
的解的存在性已经建立,那么现在只需证明解的唯一性和其特征表示。注意
和
的解只差一个标量因子,所以我们只需证明
的解情形。
由引理3.5中
的仿射性质,我们可以假设K的
的解的椭球为欧氏单位球
,那么极值问题
可描述为:对于
,使得
(17)
这个又等价于
(18)
事实上,由引理3.1知,(17)式藴涵着
,即
。由此和
在区间
上的单调递增性,我们立即知道(18)式成立。
为了建立
极值问题的特征性质,我们需要引进一些定义和记号。若T是一非奇异的
矩阵,那么T能表示成
,其中R是对称正定矩阵,A是正交矩阵 [3]。于是我们可把一个
对称矩阵
看成是点
这样所有
对称正定矩阵可表示成一开凸锥
,其顶点在
的原点O。由于
中的非奇异线性变换可看成一非奇异的
矩阵,那么由上面的论述可知,在正交变换下,
极值问题可以建立在
上。设
和
,考虑到(18)式,我们定义泛函
为
对于任意
。引理3.3和
说明泛函F是连续的。显然
。
引理4.2:若
以及
,那么
是一闭凸区域,且在边界点
的邻域内光滑。而且
是
在
的外法向量。
证明:F的定义和
的严格单调性意味着F在
中通过顶点O的每一条射线
上是由0到
严格递增的,又由F的连续性可得
是
中的一闭区域。
为了证明区域
是凸的和光滑的,只需证明函数F是凸的和光滑的。
事实上,设
,那么由
的单调性和凸性,我们有
则F在
中是凸的。
由于F是凸的,为了证明F是光滑的,只需证明对任意
,F关于A的表值
的偏导数存在 [31]。假设
是一有界数,令矩阵
和A具有相同的表值,除了
代换
。那么由Cauchy-Schwarz不等式,对任意
有
再由
的凸性,
,
和
的有界性,可得函数
在
的每一个有界集上是Lipschitz的。因此,
(19)
在
上有界。
由于
是凸的,那么它在
几乎处处可微 [30] [31]。又因为A是一非奇异矩阵,则
在
几乎处处对所有的
可微。基本的计算可得,对几乎所有的
,
(20)
由(19)式,(20)式和Lebesgue有界收敛定理,我们得到F关于
的偏导数表达式:
对于
。
这样,F关于
的所有偏导数存在。由于F是凸的,则F是光滑的。令
,那么F关于
的梯度可写成:
(21)
显然
。由于
是闭凸的光滑区域,再结合隐函数存在定理我们便得到所需要的结果。
由(18)式和F的定义,我们可以把优化问题
转化为如下极值问题:函数F达到最小值当且仅当
,也就是说,
是F的最小值位置。
优化问题
的解的唯一性和特征表示可建立如下:
引理4.3:若
以及
,那么在正交变换下,
是F的关于保体积线性变换的唯一的最小值位置。而且,
是F的最小值位置当且仅当
(22)
对于适当的
。
证明:设
那么集合
是
中闭的、光滑的且具有非空内部的凸集。而且
是
在边界点
的内法向量 [1] [2]。由引理4.2,区域
是凸的且在
的邻域内光滑。因此,我们断言区域
和
在它们的公共边界点
相切。如果断言不成立,那么区域
和
将有重叠,于是存在一
矩阵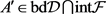 。由
是F的最小值位置假设,我们得到
。由
是F的最小值位置假设,我们得到
这便产生了矛盾。于是区域
和
在它们的公共边界点
相切,这也意味着
是F的唯一的最小值位置。
如果
是F的最小值位置,那么区域
和
在它们的公共边界点
相切。这样,
在
的外法向量
是
在
的内法向量的倍数。因此由(21)可得
对于适当的
。
另一方面,由于
是区域
和
的公共边界点,由(21)式和(22)式,
在
的外法向量和
在
的内法向量指向相同,那么区域
和
有公共边界点
,这也意味着
是F的最小值位置。
定理1.1的证明:
的解的存在性和唯一性已经在引理4.1和引理4.3中建立,下面只需证明(1)式和(22)式的等价性。注意到(13)式和(14)式,我们可限制线性变换
为
。
由引理3.5,存在
使得
设(22)成立,则由(22)式可知
是
的最小值位置当且仅当
对于适当的
,这意味着对任意
,
(23)
令
,则
。注意到
和
(24)
可得
由此可知对任意的
,
(25)
由于
,于是,由(25)式可知对任意的
,有
即(1)式成立。
反之,若(1)式成立,从而(25)式亦成立,即对任意的
,
令
。利用(24)并注意到
,可得
这个等价于对任意的
,
即(23)式和(22)式同时成立。这就完成了定理1.1的证明。
5. 对偶Orlicz John椭球的一些性质
由(13)式,(14)式和对偶Orlicz John椭球的定义,我们立即可得到下面的结果。
引理5.1:若
,那么对于
,
显然,
。由引理5.1,我们可看到如果E是原点对称椭球,那么
。
引理5.2:设
,且
使得
,其中
是满足条件的最佳实数。那么
证明:设
是椭球
的通径,
。注意到对于所有的
,
因此,由规范化的对偶Orlicz John椭球的定义,
的凸性和体积的极坐标公式(8),可得
这意味着
由椭球
的定义和上式,可得
(26)
现在我们来估计
在
条件下的值。令
,那么
即
(27)
(26)式和(27)式结合,即得
引理5.2得证。
我们知道
是唯一满足
(28)
的椭球,那么我们可以建立对偶Orlicz John椭球关于
的连续性。
引理5.3:若
以及
,那么
证明:运用(28)式,引理3.3和引理3.4,我们得到
定理5.1:若
以及
,那么
证明:根据引理1.1,我们只需证明第二个等式,而第一个等式由
便可得到。运用反证法,假设第二个等式不成立,那么由引理5.2,Blaschke选择定理和我们的假设,可知
由于
的解是唯一的,由引理3.4可得
这与引理5.3相矛盾。
由(12)式和对偶Orlicz John椭球的定义,我们立即得到如下定理。
定理5.2:如果
以及
使得
,那么
和K的体积关系可以叙述如下:
定理5.3:设
以及
,那么
(29)
等号成立当且仅当K是一个中心在原点的椭球。
证明:由
的定义和对偶Orlicz-Minkowski不等式(15),我们有
也就是说
等号成立的条件由对偶Orlicz-Minkowski不等式等号成立的条件以及对于任意
,
得到。即不等式(29)等号成立当且仅当K是一个中心在原点的椭球。
注意到如果
,那么
,
就是对偶Lp-John椭球
,于是不等式(29)变成熟知的不等式 [6]:
等号成立当且仅当K是一个中心在原点的椭球。
基金项目
国家自然科学基金资助项目(批准号:11561020)。
文章引用
马统一. 对偶Orlicz-John椭球的再讨论
Further Discussion of Dual Orlicz-John Ellipsoids[J]. 应用数学进展, 2018, 07(11): 1458-1476. https://doi.org/10.12677/AAM.2018.711170
参考文献
- 1. Lutwak, E., Yang, D. and Zhang, G. (2005) Lp-John Ellipsoids. Proceedings of the London Mathematical Society, 90, 497-520. https://doi.org/10.1112/S0024611504014996
- 2. Giannopoulos, A. and Papadimitrakis, M. (1999) Iso-tropic Surface Area Measures. Mathematika, 46, 1-13.
https://doi.org/10.1112/S0025579300007518
- 3. Petty, C.M. (1961) Surface Area of a Convex Body under Af-fine Transformations. Proceedings of the American Mathematical Society, 12, 824-828. https://doi.org/10.1090/S0002-9939-1961-0130618-0
- 4. Lutwak, E., Yang, D. and Zhang, G. (2000) A New Ellipsoid Associated with Convex Bodies. Duke Mathematical Journal, 104, 375-390. https://doi.org/10.1215/S0012-7094-00-10432-2
- 5. Lutwak, E. (1993) The Brunn-Minkowski-Firey Theory I: Mixed Volumes and the Minkowski Problem. Journal of Differential Geometry, 38, 131-150. https://doi.org/10.4310/jdg/1214454097
- 6. Yu, W., Leng, G. and Wu, D. (2007) Dual Lp-John Ellipsoids. Pro-ceedings of the Edinburgh Mathematical Society, 50, 737-753.
- 7. Lutwak, E. (1996) The Brunn-Minkowski-Firey Theory II: Affine and Geominimal Surface Areas. Advances in Mathematics, 118, 244-294. https://doi.org/10.1006/aima.1996.0022
- 8. Lutwak, E., Yang, D. and Zhang, G. (2010) Orlicz Projection Bodies. Advances in Mathematics, 223, 220-242.
https://doi.org/10.1016/j.aim.2009.08.002
- 9. Lutwak, E., Yang, D. and Zhang, G. (2010) Orlicz Centroid Bodies. Journal of Differential Geometry, 84, 365-387.
https://doi.org/10.4310/jdg/1274707317
- 10. Ludwig, M. (2005) Minkowski Valuations. Transactions of the American Mathematical Society, 357, 4191-4213.
https://doi.org/10.1090/S0002-9947-04-03666-9
- 11. Haberl, C. and Schuater, F. (2009) Asymmetric Affine Lp Sobolev Inequalities. Journal of Functional Analysis, 257, 641-658. https://doi.org/10.1016/j.jfa.2009.04.009
- 12. Haberl, C. and Schuater, F. (2009) General Lp Affine Isoperimetric Inequalities. Journal of Differential Geometry, 83, 1-26. https://doi.org/10.4310/jdg/1253804349
- 13. Haberl, C., Lutwak, E., Yang, D., et al. (2010) The Even Orlicz Minkowski Problem. Advances in Mathematics, 224, 2485-2510. https://doi.org/10.1016/j.aim.2010.02.006
- 14. Ma, T. and Wang, W. (2016) Dual Orlicz Geominimal Surface Area. Journal of Inequalities and Applications, 56, 1-13.
https://doi.org/10.1186/s13660-016-1005-4
- 15. Ma, T. (2018) On the Reverse Orlicz Blaschke-Santal’o Inequality. Mediterranean Journal of Mathematics, 32, 1-11.
- 16. Ma, T. (2016) The Minimal Dual Orlicz Surface Area. Taiwanese Journal of Mathematics, 20, 287-309.
- 17. Gardner, R.J., Hu, D. and Weil, W. (2014) The Or-licz-Brunn-Minkowski Theory: A General Framework, Additions, and Inequalities. Journal of Differential Geometry, 97, 427-476. https://doi.org/10.4310/jdg/1406033976
- 18. Xi, D., Jin, H. and Leng, G. (2014) The Orlicz Brunn-Minkowski Inequality. Advances in Mathematics, 260, 350-374.
https://doi.org/10.1016/j.aim.2014.02.036
- 19. Xiong, G. and Zou, D. (2014) Orlicz Mixed Quermassintegrals. Science China Mathematics, 57, 1-14.
https://doi.org/10.1007/s11425-014-4812-4
- 20. Zou, D. and Xiong, G. (2014) The Minimal Orlicz Surface Area. Advances in Applied Mathematics, 61, 25-45.
https://doi.org/10.1016/j.aam.2014.08.006
- 21. Zhu, G. (2012) The Orlicz Centroid Inequality for Star Bodies. Advances in Applied Mathematics, 48, 432-445.
https://doi.org/10.1016/j.aam.2011.11.001
- 22. Zhu, B., Zhou, J. and Xu, W. (2014) Dual Or-licz-Brunn-Minkowski Theory. Advances in Mathematics, 264, 700-725.
https://doi.org/10.1016/j.aim.2014.07.019
- 23. Lin, Y. (2017) Affine Orlicz Póya-Szegö Principle for Log-Concave Functions. Journal of Functional Analysis, 273, 3295-3326. https://doi.org/10.1016/j.jfa.2017.08.017
- 24. Zou, D. and Xiong, G. (2014) Orlicz-John Ellipsoids. Advances in Mathematics, 265, 132-168.
https://doi.org/10.1016/j.aim.2014.07.034
- 25. Zou, D. and Xiong, G. (2014) Orlicz-Legendre Ellipsoids. Journal of Geometric Analysis, 26, 1-29.
- 26. Li, A. (2010) Extremal Problems in Theory of Convex Geometrical Functional Analysis. Doctoral Dissertation, Shanghai University, Shanghai.
- 27. Gruber, P.M. and Schuster, F. (2005) An Arithmetic Proof of John’s Ellipsoid Theorem. Archiv der Mathematik, 85, 82-88. https://doi.org/10.1007/s00013-005-1326-x
- 28. Gruber, P.M. (2008) Application of an Idea of Voronoi to John Type Problems. Advances in Mathematics, 218, 309-351. https://doi.org/10.1016/j.aim.2007.12.005
- 29. Gardner, R.J., Daniel, H., Wolfgang, W., et al. (2015) The Dual Orlicz-Brunn-Minkowski Theory. Journal of Mathematical Analysis and Applications, 430, 810-829. https://doi.org/10.1016/j.jmaa.2015.05.016
- 30. Gruber, P.M. (2007) Convex and Discrete Geometry. Grundlehren der Mathematischen Wissenschaften, Vol. 336, Springer, Ber-lin.
- 31. Schneider, R. (1993) Convex Bodies: The Brunn-Minkowski Theory. Encyclopedia of Mathematics and Its Applications, Vol. 44, Cambridge University Press, Cambridge.
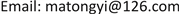





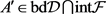 。由
是F的最小值位置假设,我们得到
。由
是F的最小值位置假设,我们得到