Sawada-Kotera-Kadovtsev-Petviashvili方程的Lump解 Lump Solution for Sawada-Kotera-Kadovtsev Petviashvili Equation

doi:10.12677/AAM.2020.97128

Advances in Applied Mathematics
Vol. 09 No. 07 ( 2020 ), Article ID: 36752 , 8 pages
10.12677/AAM.2020.97128

Lump Solution for Sawada-Kotera-Kadovtsev Petviashvili Equation

Huiqin Xu, Shan Yin

●How to Cite this Article

College of Sciences, Inner Mongolia University of Technology, Hohhot Inner Mongolia

Received: Jul. 5^th, 2020; accepted: Jul. 21^st, 2020; published: Jul. 28^th, 2020

ABSTRACT

Using the symbolic calculation software Mathematics and the Hirota bilinear operator, the lump solutions of the Sawada-Kotera-Kadomtsev-Petviashvili equation are discussed. We have obtained 7-case lump solutions. We choose one-kind lump solution of them. Its 3D graphics and contour maps are given, when the parameters included in the lump solution take special values. From those graphics, one can observe the characteristics of this lump solution with the increase of time t.

Keywords:Lump Solution, Sawada-Kotera-Kadomtsev-Petviashvili Equation

Sawada-Kotera-Kadovtsev-Petviashvili方程的Lump解

徐慧琴，银山

内蒙古工业大学理学院，内蒙古呼和浩特

收稿日期：2020年7月5日；录用日期：2020年7月21日；发布日期：2020年7月28日

摘要

利用符号计算软件Mathematics和Hirota双线性算子，研究了Sawada-Kotera-Kadomtsev-Petviashvili方程的lump解。我们得到了该方程的7类lump解，选取一类lump解，当参数取特值时，给出了不同的t值对应的3D图形和等高线图。由此可以观察到这个lump解随时间t的增加而变化的特性。

关键词 :Lump解，Sawada-Kotera-Kadomtsev-Petviashvili方程

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

许多物理和力学现象都是非线性的。例如，1895年D. J. Korteweg和G. de Vries [1] 发现水波现象是非线性的，并给出了著名的Korteweg-de Vries (KdV)方程；Von Kárman [2] 首次指出薄板挠度问题是非线性问题，并且1940年给出了该问题的控制方程——著名的Kárman方程式。因此求解非线性微分方程成为应用数学领域的一个热点问题。迄今为止，许多研究者提出并发展了求解非线性微分方程的各种方法，如Lie对称 [3]、Hirota双线性法 [4] [5] [6]、同伦摄动法 [7] [8]、同伦分析法 [9]、Adomian分解法 [10] [11] (ADM)、辅助方程法 [12] [13] [14]、Bäcklund变换和Hirota双线性法的结合 [15] [16] [17] [18] [19] 等。

其中，Hirota双线性方法是日本著名数学、物理学家Ryogo Hirota [4] 提出的一种求解非线性微分方程的方法。近年来，通过Hirota双线性方法，研究了lump解与反应解。例如：YTSF方程的lump解与反应解 [20]，(2 + 1)维非线性发展方程的反应解 [21]，(3 + 1)维非线性发展方程的精确解 [22]，降维双线性方程的lump解 [23]，广义(3 + 1)维Kadomtsev-Petviashvili方程的lump解 [24]；非局部KPI方程的lump解 [25]；新的广义Kadomtsev-Petviashvili方程的lump解 [26]；2 + 1维Korteweg-de-Vries方程的个一般lump解 [27]；Boiti-Leon-Manna-Pempinelli (BLMP)方程的lump解 [28]；广义变系数Kadomtsev-Petviashvili方程的lump解 [29]；Ito方程的lump解 [30]；Boussinesq波方程的lump单孤子解和lump双孤子解 [31]；(3 + 1)维BKP-Boussinesq方程及其降维方程的lump解 [32]；(3 + 1)维广义B型Kadomtsev-Petviashvili方程的lump解、lump孤子解和lump条孤子解 [33]；Sawada-Kotera (SK)方程的lump解 [34]；三阶非线性发展方程的lump解和反应解 [35]；(2 + 1)维非对称Nizhnik-Novikov-Veselov方程lump解和lump条状解 [36] 等等。

用Hirota双线性方法从一个非线性微分方程出发，构造一个具有物理意义的非线性微分方程也是可能的。基于Hirota双线性方法，Wazwaz [37] 结合Sawada-Kotera (SK)方程与Kadomtsev-Petviashvili (KP)方程提出了Sawada-Kotera-Kadomtsev-Petviashvili (SKKP)方程。Sawada-Kotera-Kadomtsev Petviashvili (SK-KP)方程如下：

${(u_{t} + 15 u u_{x x x} + 15 u_{x} u_{x x} + 45 u^{2} u_{x} + u_{x x x x x})}_{x} + u_{y y} = 0$ (1)

在变换 $u = 2 {(\ln f)}_{x x}$ 下SK-KP方程变为以下Hirota双线性形式：

$\begin{array}{l} B_{SK-KP} (f) : = (D_{x} D_{t} + D_{x}^{6} + D_{y}^{2}) f \cdot f \\ = 2 (- f_{y}^{2} - f_{t} f_{x} - 10 f_{x x x}^{2} + 15 f_{x x} f_{x x x x} - 6 f_{x} f_{x x x x x}) + f (f_{y y} + f_{x} f_{t} + f_{x x x x x x}) \\ = 0 \end{array}$ (2)

其中双线性算子如下： $D_{t}^{n} D_{x}^{m} a \cdot b = {{(\frac{\partial}{\partial t} - \frac{\partial}{\partial t^{'}})}^{n} {(\frac{\partial}{\partial x} - \frac{\partial}{\partial x^{'}})}^{m} a (x, t) \cdot b (x^{'}, t^{'}) |}_{x^{'} = x, t^{'} = t}$ 。

基于双线性方程(2)，Wazwaz [37] 讨论了它的n-孤子解；Wazwaz利用 $\tanh - \coth$ 方法 [38] 讨论了其单孤子解；在 [39] [40] 中，利用F展开法和指数函数法讨论了SK-KP方程的精确行波解、孤立波解、新的扭波解和周期波解。

基于上述变换，本文利用Hirota双线性方法和符号计算系统Mathematics将研究SK-KP方程(1)的lump解。具体内容如下：第二节在Hirota双线性方法的基础上，讨论了SK-KP方程的lump解，得到了七类lump解；第三节给出了结论。

2. SK-KP方程的Lump解

为了讨论(1)中的Lump解，我们假设方程(2)中的f为：

$f = g^{2} + h^{2} + a_{9}$ , (3)

其中， $g = a_{1} x + a_{2} y + a_{3} t + a_{4}$ ， $h = a_{5} x + a_{6} y + a_{7} t + a_{8}$ ， $a_{i} (i = 1, 2, \dots, 9)$ 都是实数。将(3)代入式(2)，得到了关于 $a_{i} (i = 1, 2, \dots, 9)$ 的代数方程组。在求解该代数方程组，得到以下七组解和相应的方程(1)的Lump解：

第一组：

$a_{1} = a_{1}, a_{2} = 0, a_{3} = 0, a_{4} = a_{4}, a_{5} = a_{5}, a_{6} = 0, a_{7} = 0, a_{8} = a_{8}, a_{9} = a_{9}$ (4)

其中 $a_{i} (i = 1, 4, 5, 8, 9)$ 是任意实数，对应SK-KP方程的lump解如下：

$u (x, y, t) = \frac{p}{q}$ (5)

这里 $p = 2 (2 (a_{1}^{2} + a_{5}^{2}) ({(a_{1} x + a_{4})}^{2} + {(a_{5} x + a_{8})}^{2} + a_{9}) - 4 {(a_{1}^{2} x + a_{5} (a_{5} x + a_{8}) + a_{4} a_{1})}^{2})$ ，

$q = {({(a_{1} x + a_{4})}^{2} + {(a_{5} x + a_{8})}^{2} + a_{9})}^{2}$ .

第二组：当 $a_{7} \neq 0$ 时，

$a_{1} = 0, a_{2} = 0, a_{3} = 0, a_{4} = a_{4}, a_{5} = - \frac{a_{6}^{2}}{a_{7}}, a_{6} = a_{6}, a_{7} = a_{7}, a_{8} = a_{8}, a_{9} = a_{9}$ (6)

相应方程的解如下：

$u (x, y, t) = \frac{4 a_{6}^{2} (- {(a_{7} t - \frac{a_{6}^{2} x}{a_{7}} + a_{6} y + a_{8})}^{2} + a_{4}^{2} + a_{9})}{a_{7}^{2} ({(a_{7} t - \frac{a_{6}^{2} x}{a_{7}} + a_{6} y + a_{8})}^{2} + a_{4}^{2} + a_{9})}$ . (7)

第三组：

$a_{1} = a_{1}, a_{2} = 0, a_{3} = a_{3}, a_{4} = a_{4}, a_{5} = - \frac{a_{1} a_{7}}{a_{3}}, a_{6} = - \sqrt{a_{1}} \sqrt{\frac{a_{7}^{2}}{a_{3}} + a_{3}}, a_{7} = a_{7}, a_{8} = a_{8}, a_{9} = 0$ (8)

其中 $a_{3} \neq 0, a_{1} \geq 0$ 。相应的lump解为：

$u (x, y, t) = \frac{p}{q}$ (9)

这里

$\begin{matrix} p = 4 a_{1}^{2} [a_{3}^{2} (a_{3}^{2} + a_{7}^{2}) ({(x a_{1} + t a_{3} + a_{4})}^{2} + \frac{{(x a_{1} a_{7} + y \sqrt{a_{1}} a_{3} \sqrt{a_{3} + \frac{a_{7}^{2}}{a_{3}}} - a_{3} (t a_{7} + a_{8}))}^{2}}{a_{3}^{2}}) \\ \begin{matrix} _{}^{} \end{matrix} - 2 {(x a_{1} (a_{3}^{2} + a_{7}^{2}) + y \sqrt{a_{1}} a_{3} a_{7} \sqrt{a_{3} + \frac{a_{7}^{2}}{a_{3}}} + a_{3} (t a_{3}^{2} + a_{3} a_{4} - a_{7} (t a_{7} + a_{8})))}^{2}] \end{matrix}$ ,

$q = a_{3}^{4} {({(x a_{1} + t a_{3} + a_{4})}^{2} + \frac{{(x a_{1} a_{7} + y \sqrt{a_{1}} a_{3} \sqrt{a_{3} + \frac{a_{7}^{2}}{a_{3}}} - a_{3} (t a_{7} + a_{8}))}^{2}}{a_{3}^{2}})}^{2}$ .

第四组：当 $a_{3} \neq 0, a_{1} \geq 0$ 时，

$a_{1} = a_{1}, a_{2} = 0, a_{3} = a_{3}, a_{4} = a_{4}, a_{5} = - \frac{a_{1} a_{7}}{a_{3}}, a_{6} = \sqrt{a_{1}} \sqrt{\frac{a_{7}^{2}}{a_{3}} + a_{3}}, a_{7} = a_{7}, a_{8} = a_{8}, a_{9} = 0$

方程的解为：

$u (x, y, t) = \frac{p}{q}$

这里

$\begin{array}{l} p = 4 a_{1}^{2} [a_{3}^{2} (a_{3}^{2} + a_{7}^{2}) ({(x a_{1} + t a_{3} + a_{4})}^{2} + \frac{{(- x a_{1} a_{7} + y \sqrt{a_{1}} a_{3} \sqrt{a_{3} + \frac{a_{7}^{2}}{a_{3}}} + a_{3} (t a_{7} + a_{8}))}^{2}}{a_{3}^{2}}) \\ \begin{matrix} _{}^{} \end{matrix} - 2 {(x a_{1} (a_{3}^{2} + a_{7}^{2}) - y \sqrt{a_{1}} a_{3} a_{7} \sqrt{a_{3} + \frac{a_{7}^{2}}{a_{3}}} + a_{3} (t a_{3}^{2} + a_{3} a_{4} - a_{7} (t a_{7} + a_{8})))}^{2}] \end{array}$ ,

$q = a_{3}^{4} {({(x a_{1} + t a_{3} + a_{4})}^{2} + \frac{{(- x a_{1} a_{7} + y \sqrt{a_{1}} a_{3} \sqrt{a_{3} + \frac{a_{7}^{2}}{a_{3}}} + a_{3} (t a_{7} + a_{8}))}^{2}}{a_{3}^{2}})}^{2}$ .

第五组：当 $a_{6} \neq 0$ 和 $a_{6} \neq 0$ 时，

$a_{1} = - \frac{a_{2} a_{6}}{a_{7}}, a_{2} = a_{2}, a_{3} = \frac{a_{2} a_{7}}{a_{6}}, a_{4} = a_{4}, a_{5} = - \frac{a_{6}^{2}}{a_{7}}, a_{6} = a_{6}, a_{7} = a_{7}, a_{8} = a_{8}, a_{9} = a_{9}$

方程的解为：

$u (x, y, t) = \frac{p}{q}$

其中，

$\begin{matrix} p = - 4 [2 a_{2}^{3} a_{4} a_{6} a_{7} (- x a_{6}^{2} + y a_{6} a_{7} + t a_{7}^{2}) + a_{2}^{4} {(- x a_{6}^{2} + y a_{6} a_{7} + t a_{7}^{2})}^{2} \\ + 2 a_{2} a_{4} a_{6}^{3} a_{7} (- x a_{6}^{2} + y a_{6} a_{7} + a_{7} (t a_{7} + 2 a_{8})) + a_{2}^{2} a_{6}^{2} (2 x^{2} a_{6}^{4} - 4 x y a_{6}^{3} a_{7} \\ + 2 y a_{6} a_{7}^{2} (2 t a_{7} + a_{8}) - 2 a_{6}^{2} a_{7} ((2 t x - y^{2}) a_{7} + x a_{8}) + a_{7}^{2} (a_{4}^{2} + 2 t^{2} a_{7}^{2} + 2 t a_{7} a_{8} - a_{8}^{2} - a_{9})) \\ + a_{6}^{4} (x^{2} a_{6}^{4} - 2 x y a_{6}^{3} a_{7} + 2 y a_{6} a_{7}^{2} (t a_{7} + a_{8}) + a_{6}^{2} a_{7} ((- 2 t x + y^{2}) a_{7} - 2 x a_{8}) \\ + a_{7}^{2} (- a_{4}^{2} + t^{2} a_{7}^{2} + 2 t a_{7} a_{8} + a_{8}^{2} - a_{9}))] \end{matrix}$ ,

$q = a_{7}^{4} {(\frac{{(a_{4} a_{6} a_{7} + a_{2} (- x a_{6}^{2} + y a_{6} a_{7} + t a_{7}^{2}))}^{2}}{a_{6}^{2} a_{7}^{2}} + {(y a_{6} - \frac{x a_{6}^{2}}{a_{7}} + t a_{7} + a_{8})}^{2} + a_{9})}^{2}$ .

第六组：当 $a_{3} \neq 0$ 时，

$a_{1} = - \frac{a_{2}^{2}}{a_{3}}, a_{2} = a_{2}, a_{3} = a_{3}, a_{4} = a_{4}, a_{5} = 0, a_{6} = 0, a_{7} = 0, a_{8} = a_{8}, a_{9} = a_{9}$

方程的解为：

$u (x, y, t) = \frac{4 a_{2}^{2} (- {(a_{3} t - \frac{a_{2}^{2} x}{a_{3}} + a_{2} y + a_{4})}^{2} + a_{8}^{2} + a_{9})}{a_{3}^{2} {({(a_{3} t - \frac{a_{2}^{2} x}{a_{3}} + a_{2} y + a_{4})}^{2} + a_{8}^{2} + a_{9})}^{2}}$ .

第七组：当 $a_{3}^{2} + a_{7}^{2} \neq 0$ 时，

$\begin{array}{l} a_{1} = \frac{- a_{3} a_{2}^{2} - 2 a_{6} a_{7} a_{2} + a_{3} a_{6}^{2}}{a_{3}^{2} + a_{7}^{2}}, a_{2} = a_{2}, a_{3} = a_{3}, a_{4} = a_{4}, \\ a_{5} = \frac{a_{7} a_{2}^{2} - 2 a_{3} a_{6} a_{2} - a_{7} a_{6}^{2}}{a_{3}^{2} + a_{7}^{2}}, a_{6} = a_{6}, a_{7} = a_{7}, a_{8} = a_{8}, a_{9} = 0 \end{array}$

方程的解为：

$u (x, y, t) = \frac{p}{q}$ ,

其中，

$\begin{matrix} p = 4 {- 2 [- x a_{2}^{4} + y a_{2}^{3} a_{3} + a_{2}^{2} (t a_{3}^{2} + a_{3} a_{4} - 2 x a_{6}^{2} + y a_{6} a_{7} - a_{7} (t a_{7} + a_{8})) \\ + {a_{6}^{2} (- t a_{3}^{2} - a_{3} a_{4} - x a_{6}^{2} + y a_{6} a_{7} + a_{7} (t a_{7} + a_{8})) + a_{2} a_{6} (2 a_{4} a_{7} + a_{3} (y a_{6} + 4 t a_{7} + 2 a_{8}))]}^{2} \\ + {(a_{2}^{2} + a_{6}^{2})}^{2} [(x^{2} a {}_{2}^{4}- 2 x y a_{2}^{3} a_{3} + t^{2} a_{3}^{4} + 2 t a_{3}^{3} a_{4} + x^{2} a_{6}^{4} - 2 x y a_{6}^{3} a_{7} + a_{4}^{2} a_{7}^{2} - 2 t x a_{6}^{2} a_{7}^{2} \\ + y^{2} a_{6}^{2} a_{7}^{2} + 2 t y a_{6} a_{7}^{3} + t^{2} a_{7}^{4} + 2 a_{3} a_{4} (x a_{6}^{2} + t a_{7}^{2}) - 2 x a_{6}^{2} a_{7} a_{8} + 2 y a_{6} a_{7}^{2} a_{8} + 2 t a_{7}^{3} a_{8} \end{matrix}$

$\begin{matrix} + a_{7}^{2} a_{8}^{2} + a_{3}^{2} (a_{4}^{2} + (2 t x + y^{2}) a_{6}^{2} + 2 t^{2} a_{7}^{2} + 2 t a_{7} a_{8} + a_{8}^{2} + 2 y a_{6} (t a_{7} + a_{8})) \\ + a_{2}^{2} ((- 2 t x + y^{2}) a_{3}^{2} - 2 x a_{3} a_{4} + 2 x^{2} a_{6}^{2} - 2 x y a_{6} a_{7} + a_{7} ((2 t x + y^{2}) a_{7} + 2 x a_{8})) \\ + 2 a_{2} (t y a_{3}^{3} + y a_{3}^{2} a_{4} + a_{4} a_{7} (- 2 x a_{6} + y a_{7}) - a_{3} (x y a_{6}^{2} - t y a_{7}^{2} + 2 x a_{6} (2 t a_{7} + a_{8})))]} \end{matrix}$

$\begin{matrix} q = {(a_{3}^{2} + a_{7}^{2})}^{2} [\frac{{(- x a_{2}^{2} a_{3} + t a_{3}^{3} + a_{3}^{2} a_{4} + a_{4} a_{7}^{2} + a_{3} (x a_{6}^{2} + t a_{7}^{2}) + a_{2} (y a_{3}^{2} + a_{7} (- 2 x a_{6} + y a_{7})))}^{2}}{{(a_{3}^{2} + a_{7}^{2})}^{2}} \\ {+ {(y a_{6} + t a_{7} + \frac{x (- 2 a_{2} a_{3} a_{6} + a_{2}^{2} a_{7} - a_{6}^{2} a_{7})}{a_{3}^{2} + a_{7}^{2}} + a_{8})}^{2}]}^{2} \end{matrix}$ .

3. 结论

本文借助于符号计算系统Mathematics和双线性算子，研究了SKKP方程的Lump解。我们得到了7组lump解。由此说明SKKP方程的解的丰富性和部分解的特征以便理解该方程的可积性。当 $a_{1} = 4, a_{3} = 3, a_{4} = 2, a_{7} = 0, a_{8} = 3$ 时，解(9)的3D图和等高线图如图1所示，可以观察到随着时间该lump解沿着轴向正方向移动。

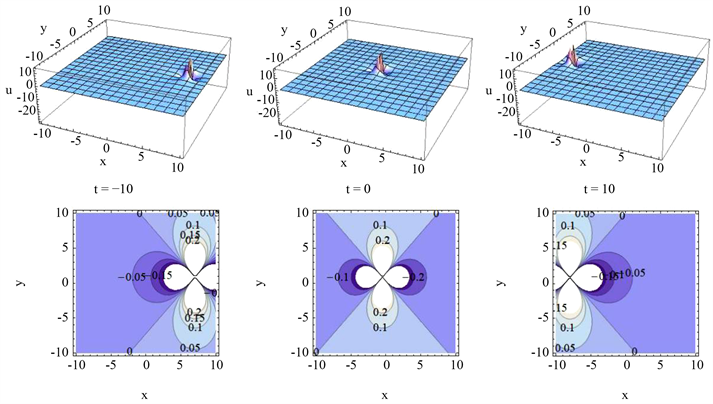
Figure 1. 3D plot and contour plot of solution (9)

图1. 解(9)的3D图和等高线图( $a_{1} = 4, a_{3} = 3, a_{4} = 2, a_{7} = 0, a_{8} = 3$ )

致谢

感谢银山老师的支持与帮助。

文章引用

徐慧琴,银山. Sawada-Kotera-Kadovtsev-Petviashvili方程的Lump解
Lump Solution for Sawada-Kotera-Kadovtsev Petviashvili Equation[J]. 应用数学进展, 2020, 09(07): 1084-1091. https://doi.org/10.12677/AAM.2020.97128

参考文献

1. Korteweg, D.J. and de Vries, G. (1895) On the Change of Form of Long Waves Advancing in a Rectangular Canal, and on a New Type of Long Stationery Waves. Philosophical Magazine, 39, 422-443. https://doi.org/10.1080/14786449508620739

2. von Karman (1940) The Engineer Grapples with Nonlinear Problems. Bulletin of the American Mathematical Society, 46, 615-683. https://doi.org/10.1090/S0002-9904-1940-07266-0

3. Yun, Y.S. and Temuer, C. (2015) Classical and Nonclassical Symmetry Classifications of Non-Linear Wave Equation with Dissipation. Applied Mathematics and Mechanics (English Edition), 36, 365-378. https://doi.org/10.1007/s10483-015-1910-6

4. Hirota, R. (2004) The Direct Method in Soliton Theory. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511543043

5. Ma, W.X. (2015) Lump Solutions to the Kadomtsev-Petviashvili Equation. Physics Letters A, 379, 1975-1978. https://doi.org/10.1016/j.physleta.2015.06.061

6. Ma, W.X. and Zhou, Y. (2016) Lump Solutions to Nonlinear Partial Differential Equations via Hirota Bilinear Forms. Journal of Differential Equations, 264, 2633-2659.

7. Yun, Y.S. and Temuer, C. (2015) Application of the Homotopy Perturbation Method for the Large Deflection Problem of a Circular Plate. Applied Mathematical Modelling, 39, 1308-1316. https://doi.org/10.1016/j.apm.2014.09.001

8. Yun, Y.S. and Temuer, C. (2013) Homotopy Perturbation Method for Viscous Heating in Plane Couette Flow. Thermal Science, 17, 1355-1360. https://doi.org/10.2298/TSCI1305355Y

9. Liao, S.J. (1992) He Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. PhD Thesis, Shanghai Jiao Tong University, Shanghai.

10. Adomian, G. (1988) A Review of the Decomposition Method in Applied Mathematics. Journal of Mathematical Analysis and Applications, 135, 501-544. https://doi.org/10.1016/0022-247X(88)90170-9

11. Rach, R. (2008) A New Definition of the Adomian Polynomials. Kybernetes, 37, 910-955. https://doi.org/10.1108/03684920810884342

12. Fan, E.G. (2000) Extended Tanh-Function Method and Its Applications to Nonlinear Equations. Physics Letters A, 277, 212-220. https://doi.org/10.1016/S0375-9601(00)00725-8

13. Yun, Y.S. and Temuer, C. (2011) A Further Improved Tanh Method and New Traveling Wave Solutions of 2D-KdV Equation. Journal of Inner Mongolia University (Natural Science Edition), 42, 604-609.

14. Gao, L.-N., Zhao, X.-Y., Zi, Y.-Y., Yu, J. and Lv, X. (2016) Resonant Behavior of Multiple Wave Solutions to a Hirota Bilinear Equation. Computers and Mathematics with Applications, 72, 1225-1229. https://doi.org/10.1016/j.camwa.2016.06.008

15. Chen, S.-J., Ma, W.-X. and Lv, X. (2020) Bäcklund Transformation, Exact Solutions and Interaction Behaviour of the (3 + 1)-Dimensional Hirota-Satsuma-Ito-Like Equation. Communications in Nonlinear Science and Numerical Simulation, 83, Article ID: 105135. https://doi.org/10.1016/j.cnsns.2019.105135

16. Xu, H.-N., Ruan, W.-Y., Zhang, Y. and Lv, X. (2020) Multi-Exponential Wave Solutions to Two Extended Jimbo-Miwa Equations and the Resonance Behavior. Applied Mathematics Letters, 99, Article ID: 105976. https://doi.org/10.1016/j.aml.2019.07.007

17. Xia, J.-W., Zhao, Y.-W. and Lv, X. (2020) Predictability, Fast Calculation and Simulation for the Interaction Solution to the Cylindrical Kadomtsev-Petviashvili Equation. Communications in Nonlinear Science and Numerical Simulation, 88, Article ID: 105260. https://doi.org/10.1016/j.cnsns.2020.105260

18. Gao, L.-N., Zi, Y.-Y., Yin, Y.-H., Ma, W.-X. and Lv, X. (2017) Bäcklund Transformation, Multiple Wave Solutions and Lump Solutions to a (3 + 1)-Dimensional Nonlinear Evolution Equation. Nonlinear Dynamics, 89, 2233-2240. https://doi.org/10.1007/s11071-017-3581-3

19. Lv, X., Lin, F.-H. and Qi, F.-H. (2015) Analytical Study on a Two-Dimensional Korteweg-de Vries Model with Bilinear Representation, Bäcklund Transformation and Soliton Solutions. Applied Mathematical Modelling, 39, 3221-3226. https://doi.org/10.1016/j.apm.2014.10.046

20. Chen, S.-J., Yin, Y.-H., Ma, W.-X. and Lv, X. (2019) Abundant Exact Solutions and Interaction Phenomena of the (2 + 1)-Dimensional YTSF Equation. Analysis and Mathematical Physics, 9, 2329-2344. https://doi.org/10.1007/s13324-019-00338-2

21. Hua, Y.-F., Guo, B.-L., Ma, W.-X. and Lv, X. (2019) Interaction Behavior Associated with a Generalized (2 + 1)-Dimensional Hirota Bilinear Equation for Nonlinear Waves. Applied Mathematical Modelling, 74, 184-198. https://doi.org/10.1016/j.apm.2019.04.044

22. Yin, Y.-H., Ma, W.-X., Liu, J.-G. and Lv, X. (2018) Diversity of Exact Solutions to a (3 + 1)-Dimensional Nonlinear Evolution Equation and Its Reduction. Computers and Mathematics with Applications, 76, 1275-1283. https://doi.org/10.1016/j.camwa.2018.06.020

23. Lv, X. and Ma, W.-X. (2016) Study of Lump Dynamics Based on a Dimensionally Reduced Hirota Bilinear Equation. Nonlinear Dynamics, 85, 1217-1222. https://doi.org/10.1007/s11071-016-2755-8

24. Guan, X., Liu, W.-J., Zhou, Q. and Biswas, A. (2020) Some Lump Solutions for a Generalized (3 + 1)-Dimensional Kadomtsev-Petviashvili Equation. Applied Mathematics and Computation, 366, Article ID: 124757. https://doi.org/10.1016/j.amc.2019.124757

25. Zhang, X.E., Chen, Y. and Zhang, Y. (2017) Breather, Lump and X Soliton Solutions to Nonlocal KP Equation. Computers and Mathematics with Applications, 74, 2341-2347. https://doi.org/10.1016/j.camwa.2017.07.004

26. Yu, J., Ma, W.-X. and Chen, S.-T. (2019) Lump Solutions of a New Generalized Kadomtsev-Petviashvili Equation. Modern Physics Letters B, 33, Article ID: 1950126. https://doi.org/10.1142/S0217984919501264

27. Wang, H., Tian, S.-F., Zhang, T.-T., Chen, Y. and Fang, Y. (2019) General Lump Solutions, Lump Off Solutions, and Rogue Wave Solutions with Predictability for the (2 + 1)-Dimensional Korteweg-de Vries Equation. Computational and Applied Mathematics, 38, 164. https://doi.org/10.1007/s40314-019-0938-x

28. Ali, M.R. and Ma, W.-X. (2019) New Exact Solutions of Nonlinear (3 + 1)-Dimensional Boiti-Leon-Manna-Pempinelli Equation. Advances in Mathematical Physics, 2019, Article ID: 9801638. https://doi.org/10.1155/2019/9801638

29. Liu, J.-G., Eslami, M., Rezazadeh, H. and Mirzazadeh, M. (2019) Rational Solutions and Lump Solutions Toa Non-Isospectral and Generalized Variable-Coefficient Kadomtsev-Petviashvili Equation. Nonlinear Dynamics, 95, 1027-1033. https://doi.org/10.1007/s11071-018-4612-4

30. Ma, H.C., Meng, X.M. and Wu, H.F. (2019) A Class of Lump Solutions for ITO Equation. Thermal Science, 23, 2205-2210. https://doi.org/10.2298/TSCI1904205M

31. Lu, D.C., Seadawy, A.R. and Ahmed, I. (2019) Applications of Mixed Lump-Solitons Solutions and Multi-Peaks Solitons for Newly Extended (2 + 1)-Dimensional Boussinesq Wave Equation. Modern Physics Letters B, 33, Article ID: 1950363.

32. Kaur, L. and Wazwaz, A.-M. (2019) Bright-Dark Lump Wave Solutions for a New Form of the (3 + 1)-Dimensional Bkp-Boussinesq Equation. Romanian Reports in Physics, 71, 102.

33. Yan, X.-W., Tian, S.-F., Wang, X.-B. and Zhang, T.-T. (2018) Solitons to Rogue Waves Transition, Lump Solutions and Interaction Solutions for the (3 + 1)-Dimensional Generalized B-Type Kadomtsev-Petviashvili Equation in Fluid Dynamics. International Journal of Computer Mathematics, 96, 1839-1848.

34. Zhang, H.-Q. and Ma, W.-X. (2017) Lump Solutions to the (2 + 1)-Dimensional Sawada-Kotera Equation. Nonlinear Dynamics, 87, 2305-2310. https://doi.org/10.1007/s11071-016-3190-6

35. Kofane, T.C., Fokou, M., Mohamadou, A. and Yomba, E. (2017) Lump Solutions and Interaction Phenomenon to the Third-Order Nonlinear Evolution Equation. The European Physical Journal Plus, 132, Article No. 465. https://doi.org/10.1140/epjp/i2017-11747-6

36. Zhao, Z.L., Chen, Y. and Han, B. (2017) Lump Soliton, Mixed Lump Stripe and Periodic Lump Solutions of a (2 + 1)-Dimensional Asymmetrical Nizhnik-Novikov-Veselov Equation. Modern Physics Letters B, 31, 157-175. https://doi.org/10.1142/S0217984917501573

37. Wazwaz, A.-M. (2008) The Hirota’s Bilinear Method and the Tanh-Coth Method for Multiple-Soliton Solutions of the Sawada-Kotera-Kadomtsev-Petviashvili Equation. Applied Mathematics and Computation, 200, 160-166. https://doi.org/10.1016/j.amc.2007.11.001

38. Zhang, J.H. (2010) Exact Traveling Wave Solution of SK-KP Equation by F-Expansion Method Combined with Exponential Function Method (Natural Science). Liaocheng University, Liaocheng.

39. Zhang L.-L. (2010) Explicit Solutions of (2 + 1)-Dimensional SK-KP Equation.

40. Wang, M.L., Li, X.Z. and Zhang, J.L. (2008) The (G’G)-Expansion Method and Travelling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics. Physics Letters A, 372, 417-423. https://doi.org/10.1016/j.physleta.2007.07.051

期刊菜单