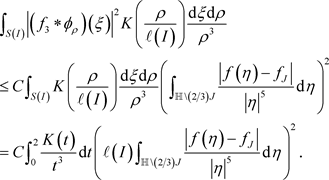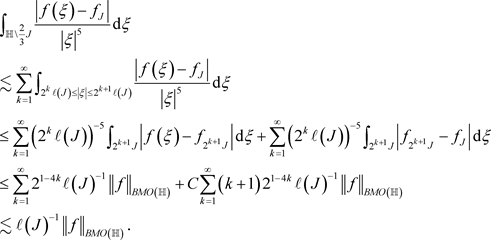青岛大学数学与统计学院,山东 青岛
收稿日期:2022年4月16日;录用日期:2022年5月17日;发布日期:2022年5月24日

摘要
本文主要引入了一类与权函数有关的新型的Q型空间
。我们首先研究了
的基本性质,从而得到了
与BMO之间的关系,最后给出了
的Carleson测度刻画。
关键词
Q型空间,权函数,Carleson测度刻画

The QK Space Related with Weight Function
Meimei Shi
School of Mathematics and Statistics, Qingdao University, Qingdao Shandong
Received: Apr. 16th, 2022; accepted: May 17th, 2022; published: May 24th, 2022

ABSTRACT
In this paper, we introduce a new class of Q type space
which is related to weight functions. Firstly, we study some properties of
and then investigate the relationship between
and BMO space. Finally, we give the Carleson measure characterization of
.
Keywords:Q Type Space, Weiht Function, Carleson Measure Characterization

Copyright © 2022 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
作为平均震荡空间的推广(BMO),Q型空间在调和分析、偏微分方程以及位势理论中得到了广泛的研究,参见文献 [1] [2] [3]。Q型空间与BMO空间有类似的性质,在许多分析性问题的研究中,Q型空间可以是BMO空间很好的替代。最初,Essén等人将
推广到了欧几里得空间,参见文献 [4]。在2004年,Dafni和Xiao在文献 [5] 中利用一种新型的帐篷空间解决了分数阶Carleson测度和
空间的几个对偶问题,定义了
的对偶为包含Hardy空间
的分布空间并证明了一个原子分解。关于Q型空间更多的内容以及研究进展,可以参见文献 [6] [7] [8]。
基于类似的想法,作为BMO型空间在
上的推广,在文献 [9] 中,王春杰将Q型空间推广到
中,引入了
空间,通过利用Poisson积分给出了Carleson测度刻画。接下来,我们重述一下文献[9]中
的概念。
定义1.1令
, 包含了
上的所有可测函数f,则f满足
其中I是
上的一个区间,
是区间I的长度,并且该式的上确界取遍
中所有的方体I。
董建锋将
的概念推广到
型群上,记为
,参见文献 [10]。在2016年,Zhao在文献 [11] 中引入了
上的Hardy-Hausdorff空间,得到了Hardy-Hausdorff空间的原子分解,证明了 Hardy-Hausdorff空间与
空间的对偶性。
通过定义1.1我们可以看出,空间
与幂函数
有关。一个很自然的问题就是
中的幂函数
是否可以用一个单调递增的权函数替代。因此,我们引入和研究了Heisenberg群上一个更为普遍的空间
,为了方便,本文研究
的相关问题,对于高维形式
的研究可类似,二者均可视为
的推广。
定义1.2设K是
上的增函数。若
满足
则称
。其中I是
上的一个区间,
是区间I的长度,并且该式的上确界取遍
中所有的方体I并且该式的上确界取遍
中所有的方体I。
本文的主要目的是研究
上的Q型空间
。本文主要包括如下内容:在第二部分,介绍了相关的概念,研究了
的性质,给出了
与BMO空间的关系;在第三部分,利用辅助函数给出了
的Carleson测度刻画。
在本文中,如果存在一个正的常数C满足
,可写作
。另外,如果 和
和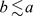 都成立,可写作
都成立,可写作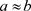 。我们假设
是单调递增的并且满足
。如下是我们将会用到的几个函数空间:
。我们假设
是单调递增的并且满足
。如下是我们将会用到的几个函数空间:

2. 的基本性质
的基本性质
在复空间
中,Siegel上半空间
被定义为
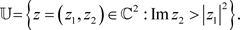
集合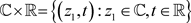 构成了Heisenberg群
,其中
。如果
,那么
构成了Heisenberg群
,其中
。如果
,那么
且
,其中
。
和
可以通过在原点进行如下的映射等同起来:
令
,f的梯度及其梯度的长度分别为
和
其中
并且
。在
中,
被称为函数f与g的卷积。
为了研究
的性质,我们需要如下辅助函数:
并且在全文中假设辅助函数
满足如下两个条件:
(1)
(2)
对于任意的方体
, 是I的中心,则基于I的Carleson盒子定义为
定义2.1令
。如果存在常数
满足
称
上的正Borel测度
为p-Carleson测度。
定理2.2
当且仅当
其中I是
上的一个区间,
是区间I的长度,并且该式的上确界取遍
中所有的方体I。
证明根据定义1.2,利用变量替换:
,我们可以得到
定义2.3令
且
。若f满足
那么,称
。其中I是
上的一个区间,
是区间I的长度,并且该式的上确界取遍
中所有的方体I。
下面我们给出空间
与
之间的关系。
定理2.4
(1)
;
(2) 若
,则
。
证明(1)假设
并且m表示Lebesgue测度。那么对于任意方体I以及
,我们有
由于K是非减函数,于是
注意到
那么
于是
即
。
(2) 若
成立。设I为一个方体,
并满足
。则
并且
由于
我们可以得到
因此
,根据(1)知
。
3. Carleson测度刻画
为了研究
的Carleson测度刻画,我们需要文献如下的Hardy型不等式,参见文献 [12]。
引理3.1令
并且
。假设
和
在区间
上是非负可测的。如果对于所有非负可测函数f,
(1)
成立,当且仅当
(2)
成立,当且仅当
在
上,用
定义Schwarz函数族。接下来我们证明与权函数有关的Stegenga型不等式。
引理3.2假设K满足
和
令
并且
满足
。那么对于任意的以
为中心的方体I和J且
,存在与
和J无关的常数
使得
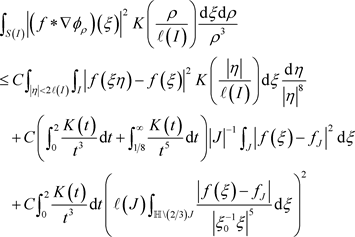
成立,其中
并且
。
证明由于
,
首先令
并且函数
满足,当
时,
, 并且
。记
,其中
且
。
是一个常数并且
表明
。因为
,
令
是
上以原点为中心的单位圆柱。设
并且
。于是
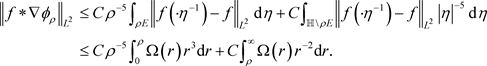
利用引理3.1,得
因此,对于
,记
其中
由于
从而
且
所以
接下来考虑
。注意到
于是
用与
相同的方法,可以得到
对于
,由于
,

如果
并且 ,则有
。因此
,则有
。因此
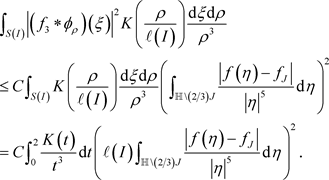
综合以上不等式,可得所证。
定理3.3假设K满足(2),
满足
。令
且
,则
当且仅当存在一个常数
满足
(3)
证明
表示
并且
。首先,若
。由定理2.4,我们可以得到
且
。令I与J是
上以原点为中心的方体,满足
,则
。那么
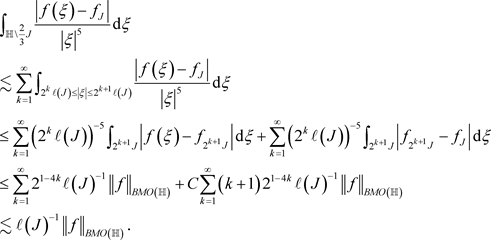
通过引理3.2我们可以推出
反过来,若(3)成立。要证
,只需证
记
,其中
,,并且
。由于
那么对于
,利用Minkowski不等式,
结合引理3.1,可以推出
又因为
对于任意满足
的
,有
对于
,易得
并且由Minkowski不等式
所以
因此通过对
和
的估计,
即
。
致谢
作者衷心感谢李澎涛教授的指导与建议。
基金项目
山东省自然科学基金(项目编号:ZR2020MA004);国家自然科学基金(项目编号:11871293)。
文章引用
石梅梅. 与权函数有关的QK空间
The QK Space Related with Weight Function[J]. 理论数学, 2022, 12(05): 784-794. https://doi.org/10.12677/PM.2022.125089
参考文献
- 1. Xiao, J. (2007) Homothetic Variant of Fractional Sobolev Space with Application to Navier-Stokes System. Dynamics of Partial Differential Equations, 2, 227-245. https://doi.org/10.4310/DPDE.2007.v4.n3.a2
- 2. Aulaskari, R., Xiao, J. and Zhao, R. (1995) On Subspaces and Subsets of BMOA and UBC. Analysis, 15, 101-121.
https://doi.org/10.1524/anly.1995.15.2.101
- 3. Wu, Z. and Xie, C. (2003) Q Spaces and Morrey Spaces. Journal of Functional Analysis, 201, 282-297.
https://doi.org/10.1016/S0022-1236(03)00020-X
- 4. Essén, M., Janson, S., Peng, Li. and Xiao, J. (2000) Q Spaces of Several Real Variables. Indiana University Mathematics Journal, 49, 575-616. https://doi.org/10.1512/iumj.2000.49.1732
- 5. Dafni, G. and Xiao, J. (2004) Some New Tent Spaces and Duality Theorems for Fractional Carleson Measures and . Journal of FunctionalAnalysis, 208, 377-422. https://doi.org/10.1016/S0022-1236(03)00181-2
- 6. Wu, Z. and Xie, C. (2003) Q Spaces and Morrey Spaces. Journal of Functional Analysis, 201, 282-297.
https://doi.org/10.1016/S0022-1236(03)00020-X
- 7. Li, P. and Zhai, Z. (2010) Well-Posedness and Regularity of Generalized Navier-Stokes Equations in Some Critical Q-Spaces. Journal of Functional Analysis, 259, 2457-2519. https://doi.org/10.1016/j.jfa.2010.07.013
- 8. Xiao, J. (2007) Homothetic Variant of Fractional Sobolev Space with Application to Navier-Stokes System. Dynamics of Partial Differential Equations, 4, 227-245. https://doi.org/10.4310/DPDE.2007.v4.n3.a2
- 9. 王春杰. 复区域上的几个问题研究[D]: [博士学位论文]. 北京: 北京大学数学系, 2003.
- 10. 董建锋. H-型群上的Q空间与Poisson积分[D]: [硕士学位论文]. 北京: 北京大学数学系, 2004.
- 11. Zhao, K. (2016) Hardy-Hausdorff Space on the Heisenberg Group. Science China Mathematics, 59, 2167-2184.
https://doi.org/10.1007/s11425-016-0062-9
- 12. Kufner, A. and Persson, L.-E. (2003) Weighted Inequalities of Hardy Type. World Scientific Publishing, River Edge, NJ, USA. https://doi.org/10.1142/5129






 和
和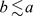 都成立,可写作
都成立,可写作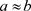 。我们假设
是单调递增的并且满足
。如下是我们将会用到的几个函数空间:
。我们假设
是单调递增的并且满足
。如下是我们将会用到的几个函数空间:
 的基本性质
的基本性质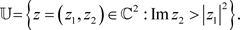
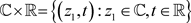 构成了Heisenberg群
,其中
。如果
,那么
构成了Heisenberg群
,其中
。如果
,那么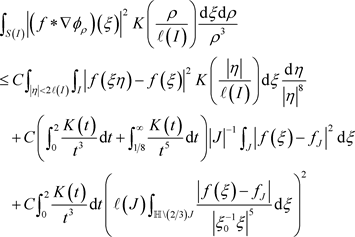
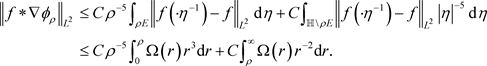

 ,则有
。因此
,则有
。因此