Computer Science and Application
Vol.
10
No.
01
(
2020
), Article ID:
34036
,
8
pages
10.12677/CSA.2020.101013
Design of a Stream Cipher Algorithm Based on Latin Square and Time-Varying Symbolic Chaotic System
Wenjun Tang, Chuanjun Tian
College of Electronics and Information Engineering, Shenzhen University, Shenzhen Guangdong

Received: Jan. 1st, 2020; accepted: Jan. 12th, 2020; published: Jan. 19th, 2020

ABSTRACT
This paper studies chaos of a class of three-dimensional time-varying generalized symbolic systems, and analyzes the pseudo-randomicity of its solutions. Then, combined with the basic cryptosystem designed by Latin square, a stream cipher algorithm was designed. Finally, the encryption effect of the algorithm on digital image is simulated and compared with the simulation results of the modulo 2 addition stream cipher system. Simulation shows that this algorithm has good encryption effects.
Keywords:Stream Cipher Algorithm, Generalized Symbolic System, Latin Square, Basic Cryptosystem

基于拉丁方与时变符号混沌系统的 流密码算法设计
唐文君,田传俊
深圳大学电子与信息工程学院,广东 深圳

收稿日期:2020年1月1日;录用日期:2020年1月12日;发布日期:2020年1月19日

摘 要
本文研究了一类三维时变广义符号动力系统的混沌性,并对它的多种伪随机性能进行了分析。在此基础上,结合拉丁方构造的基本密码系统,设计了一种多元流密码算法。最后,对该算法在数字图像上的加密效果进行了仿真,并与模2加法流密码系统的仿真结果进行了对比。仿真结果分析表明新流密码算法具有良好的加密效果和较高的安全性。
关键词 :流密码算法,广义符号动力系统,拉丁方,基本密码系统

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
众所周知,密码学中的加密算法是解决信息安全问题的有效手段之一,流密码作为现代密码学的一个重要分支,已在许多领域得到广泛应用 [1] [2] [3]。一般而言,流密码算法直接将密钥流序列与明密文序列模2加法进行加解密。但是,最近的文献 [2] 明确指出流密码算法设计可分为两个部分:一是基本密码系统设计,二是密钥流序列的设计,其中,基本密码系统可利用一组任意阶拉丁方设计,推广了利用模2加法或2阶拉丁方所设计的基本密码系统。当前,利用高于2阶拉丁方来设计基本密码系统的研究还未充分发展。另外,参照现有不少文献 [4] [5] [6] 知,可直接利用混沌系统生成的伪随机序列作为密钥流序列,因而先讨论一类新的三维时变广义符号系统。
不妨设Z为全体整数集,
, 为单边整数集,I为有界实数集,
(1)
其中,
,,, 分别为三个多元函数,并称
为系统(1)的系统函数。对任意定义在
上的三个序列
, 和
,存
在三维离散时空序列
满足(1),且
,,,对
。
称序列x为系统(1)初值为
的一个解。由文献 [4] 可知,当
和
时,可将系统(1)称为三维时变广义符号动力系统。在不混淆时,下面也将列向量写为行向量的形式。
对任一有界实数集I,记
(2)
则在
上可定义如下度量,
(3)
对任意
,。易知
是度量空间。
设
是系统(1)的一个解,
,,且
, (4)
记
,,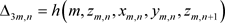 ,则系统(1)等价于式(5)中给出的无穷维离散系统:
,则系统(1)等价于式(5)中给出的无穷维离散系统:
(5)
其中,
是
上由
决定的一列映射。称系统(5)或映射列
是由系统(1)或系统函数
所导出的。
2. 新混沌系统的构造和伪随机性分析
设
,对任意
,记
,则
,, 定义如下
(6)
其中, ,
和
为周期整数数列,即存在正整数p,使得
,,,对一切
和
成立,
是三个与q互素的正整数。
,
和
为周期整数数列,即存在正整数p,使得
,,,对一切
和
成立,
是三个与q互素的正整数。
不难发现,由式(6)定义的映射
可产生三维时变广义符号系统如下
(7)
其中,
,。由于系统(7)是系统(1)的特定情形,故根据系统(1)和系统(5)的关系,系统(7)等价于如下系统(8)
,, (8)
上式中,
, 是由
所导出的映射,且对任意
,记
,,,则有
(9)
参照文献 [4] [5] [6] [7],易得如下引理及推论。
引理1:对式(8)中的映射列
,存在正整数周期p,使得
,。
推论1:设
是式(8)的系统映射,则对一切
,都有
记式(8)定义的映射列
所确定的复合映射为:
, (10)
引理2:对
和
,存在
,使
成立。
定义1:若式(1)的系统函数
所确定的映射列
或系统(5)在度量空间
上具有传递性、周期点的稠密性和初值敏感依赖性,则称
或系统(5)是Devaney混沌的,也称与系统(5)相应等价的系统(1)在
上是Devaney混沌的。
定理1:在上述条件下,系统(7)在度量空间
上是Devaney混沌的。
证明:由定义1,只需证明系统(8)在
上是Devaney混沌的。
设
且
,对
和
,存在
,使得
和
。根据
的定义知,存在
,满足
(11)
对
,记
,
其中
分别满足:
,
,.
由递推法可知,对
,,有
,,
其中
定义由式(10)给出,且有
(12)
上式中
,,G决定了映射列
、
和
。
根据引理2,对任意
和
,存在整数
,满足:
,, (13)
已知
,,由式(11)、(12)、(13)知,存在
,使
,,,其中
,且
依次满足:
,,,
其中
。故
,且
。由此可见系统(8)在
上是传递的。同理,可以类似方法证明系统(8)在
上具有周期点的稠密性和初值敏感依赖性,因而系统(8)在
上是Devaney混沌的。证毕。
例1:设
和时变离散时空系统为
(14)
其中,
,,,,,,,,对任意
。
根据现有文献无法判断系统(14)是否具有Devaney混沌性。但由于系统(14)是(7)的特殊情形,根据定理1,系统(14)是
上的Devaney混沌系统。
现对系统(14)的混沌解序列进行混乱性和自相关性仿真,图1(A)~(C)分别显示了解序列
在三维空间上的混乱程度,图1(D)~(F)分别显示解序列
的自相关程度。通过图1,不难发现,系统(14)的解序列都具有复杂的混乱性和良好的自相关性。同时,使用NIST推出的SP800-22软件检测包来测试解序列的伪随机性,从表1可知,均通过检测。由此可得,新系统的解序列具有良好伪随机性,可将其用于密钥流序列和流密码算法的设计之中。

Table 1. NIST pseudo-random sequence detection results
表1. NIST伪随机序列检测结果
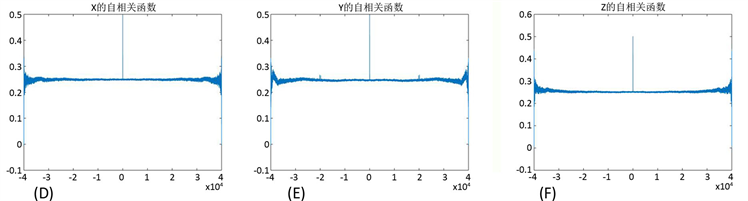
Figure 1. Confusion and correlation of solutions
图1. 解的混乱性和自相关性
3. 基于拉丁方的多元流密码算法
3.1. 算法描述
若
中的n个元素在n阶方阵L的每行每列中都出现,则称L为n阶拉丁方。显然,式(15)中的矩阵是一个16阶拉丁方。
(15)
文献 [2] 举例说明了利用4阶拉丁方构造基本密码系统的方法。目前还没有利用更高阶拉丁方来设计基本密码系统的相关研究。下面将利用式(15)中的16阶拉丁方L设计一个基本密码系统。将所有基本明文从小到大排列为一个行向量,并将拉丁方每一行作为其加密后的相应结果。例如,L的第一行所决定的置换
为
、
、
、
、
、
。
不难验证:对任意
, 、
的代数计算公式为
类似地,
均能以代数式表示,它们所决定的相应基本密码系统为
,并将相应的加解密具体步骤设计如下:
1) 设任一明文m为二元序列
,,将该二元序列按每4比特进行分组,将分组后所得到的明文单位序列设为
,其中
,等等。必要时可对m的最后一个分组填充1而组成一个4比特分组。
2) 加密变换
,,其中,取系统(14)的一个解序列作为16元密钥流序列
,可得到密文单元序列
。
3) 解密变换
,,可得到明文16元序列
。然后将每个明文单元
表示为4比特明文就得到解密后的原始二元明文序列
。
3.2. 实验结果及分析
将上述密码算法用于数字图像加解密,并将它与模2加法流密码系统进行的比较效果可参见图2。
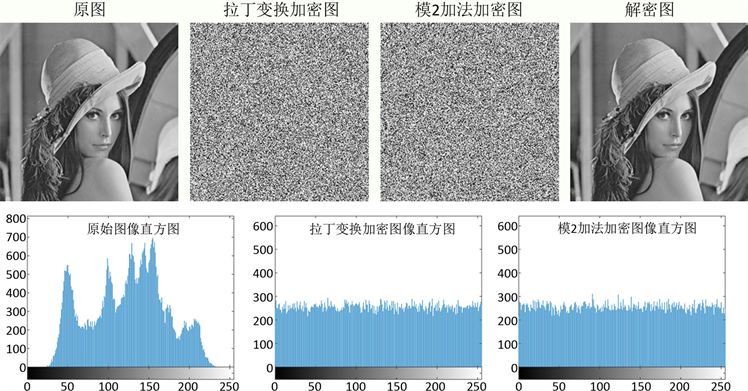
Figure 2. Encryption and decryption effect and gray level histogram
图2. 加解密效果及灰度直方图
由图2可见,两种算法都能对原始图像进行有效的加解密,密文图像的灰度直方图都接近均匀分布,能抵抗统计分析。对明文图像和两种密文图像的相邻像素相关性做仿真计算,可见表2。

Table 2. Correlation of each direction between adjacent pixels of original and encrypted graphs
表2. 原图与加密图相邻像素之间各方向的相关性
从表中可以看出,两种密文图像相邻像素相关系数都接近0,几乎不存在相关性。进一步,根据图像X信息熵的定义式(16)和最大熵原理知,由于本文所选取的Lena图像的灰度取值范围是[0,255],故图中各像素值等概率出现时最大信息熵达到8。
(16)
通过仿真计算,可得到原始图像信息熵为7.4442,新流密码系统加密图像信息熵为7.9974,模2加法流密码系统加密图像信息熵为7.9969,两种密文图的熵都比明文图的熵更接近最大理想值。综上所述,拉丁方基本密码系统在实际加密中的加密效果与传统模2加法流密码系统加密效果相差无几,且基于拉丁方基本密码系统计算复杂度更高,因而对相应流密码算法的攻击难度更大。这说明利用高阶拉丁方设计的流密码算法具有实用价值。
4. 小结
本文研究了一类新时变广义符号混沌系统,基于该系统和高阶拉丁方构造了一种与传统模2加法不同的多比特流密码算法,通过对数字图像加解密效果的分析与对比,说明了本文提出的算法具有可行性和较高的安全性。
文章引用
唐文君,田传俊. 基于拉丁方与时变符号混沌系统的流密码算法设计
Design of a Stream Cipher Algorithm Based on Latin Square and Time-Varying Symbolic Chaotic System[J]. 计算机科学与应用, 2020, 10(01): 118-125. https://doi.org/10.12677/CSA.2020.101013
参考文献
- 1. 张斌, 徐超, 冯登国. 流密码的设计与分析:回顾、现状与展望[J]. 密码学报, 2016, 3(6): 527-545.
- 2. 田传俊. 密钥非均匀分布的完善保密通信系统[J]. 通信学报, 2018, 39(11): 1-9.
- 3. Shannon, C.E. (1949) Communication Theory of Secrecy System. Bell System Technical Journal, 28, 656-715.
https://doi.org/10.1002/j.1538-7305.1949.tb00928.x
- 4. 田传俊, 陈关荣. 广义符号动力系统的混沌性[J]. 应用数学学报, 2008, 31(3): 440-446.
- 5. 田传俊, 林敬, 黎杏玲. 基于二维时变符号混沌系统的流密码算法设计[J]. 计算机科学与应用, 2018, 8(11): 1713-1719.
- 6. 田传俊, 黎杏玲, 林敬. 基于时变双边混沌符号系统的流密码算法设计[J]. 计算机科学与应用, 2018, 8(10): 1582-1588.
- 7. Tian, C. (2017) Chaos in the Sense of Devaney for Two-Dimensional Time-Varying Generalized Symbolic Dynamical Systems. International Journal of Bifurcation and Chaos, 27, Article ID: 1750060.
https://doi.org/10.1142/s0218127417500602








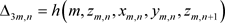 ,则系统(1)等价于式(5)中给出的无穷维离散系统:
,则系统(1)等价于式(5)中给出的无穷维离散系统: ,
和
为周期整数数列,即存在正整数p,使得
,,,对一切
和
成立,
是三个与q互素的正整数。
,
和
为周期整数数列,即存在正整数p,使得
,,,对一切
和
成立,
是三个与q互素的正整数。

