Advances in Applied Mathematics
Vol.07 No.08(2018), Article ID:26645,10
pages
10.12677/AAM.2018.78126
The Existence of Positive Solutions for a Nonlocal Boundary Value Problem
Yingli Zhu, Xiujie Yu
School of Mathematics and Statistics, Shandong Normal University, Jinan Shandong
Received: Aug. 10th, 2018; accepted: Aug. 22nd, 2018; published: Aug. 29th, 2018

ABSTRACT
This paper discusses the boundary value problem with nonlocal integral boundary conditions
where
,
; A and B are functions of bounded variation;
,
; the nonlinearity
is continuous and is allowed to change sign. According to the fixed point theorem in double cones, we obtain that there exists at least two positive solutions. And according to three-solution theorem, we obtain that there exists at least three positive solutions.
Keywords:Existence, Nonlocal Boundary Value Problem, Fixed Point Theorem, Positive Solutions

一类非局部边值问题正解的存在性
朱应丽,于秀洁
山东师范大学数学与统计学院,山东 济南
收稿日期:2018年8月10日;录用日期:2018年8月22日;发布日期:2018年8月29日

摘 要
考虑非线性非局部边值问题
其中边值条件
,
;A,B是有界变差函数;
,
;非线性项
是连续的且允许变号的。本文根据两个锥上的不动点定理,讨论得到以上问题至少存在两个正解。并且利用三解定理,讨论得到以上问题至少存在三个正解。
关键词 :存在性,非局部边值问题,不动点定理,正解

Copyright © 2018 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文考虑如下非线性非局部边值问题
(1.1)
其中边值条件(BCs)是关于线性泛函,且由Riemann-Stieltjes积分给出:
2000年,Guidotti和Merino在文献 [1] 中研究了
该方程代表了一个在稳定状态下的长度为1的加热棒模型。它在 时是绝缘的,加热或冷却操作是在
处的控制器根据传感器所反馈回的
t=0
时的温度来进行的。
时是绝缘的,加热或冷却操作是在
处的控制器根据传感器所反馈回的
t=0
时的温度来进行的。
2006年,Webb和Infante在文献 [2] 中研究了以下方程正解的存在性问题:
该方程也是一个具有稳定解的加热棒模型,不同的是,温度变化是由
处控制器通过任意点
t =η
处传感器温度变化情况反馈控制的,而不是
处。该文根据不动点指数理论,讨论了随参数的变化多个非平凡解的存在性情况。
2012年,Webb在文献 [3] 中研究了温控器模型正解的存在性:
其中,
。这是一类更为一般的边值条件,传感器为线性泛函。由于此时的传感器覆盖了加热棒的某一些点或某一连续区间,所以更符合实际。该文通过研究其格林函数的性质,讨论了以上问题何时存在多个正解以及何时不存在正解。
2015年,Infante在文献 [4] 中研究了Neumann型非局部边值问题
该文通过研究摄动Hammerstein积分方程
利用不动点指数理论,得到以上问题存在多个非平凡解。
本文在第二节,给出了相关的预备知识和引理。在第三节,我们分别通过利用两个锥上的不动点定理和Leggett-Williams三解定理得到了方程两个正解和三个正解的存在性结果。
2. 预备知识和引理
本文中,我们作如下假设:
(H1)
;
(H2)
;
(H3)
是有界变差函数,且
。
对于问题(1.1),我们将其转化为对以下相应Hammerstein积分方程解的存在性:
其中
为以下问题的Green函数:
即
则
且
令
。对
,定义
则
为一Banach空间。
,
考虑
显然,
为X中的两个锥,且
。对
,定义
令
,我们定义算子
如下:
使
注1:若
为一泛函,
 ,则
。
,则
。
引理2.1:
为全连续算子。
证明:首先我们证明
。
对
,有
,且
所以,
。
再由f的连续性及
的定义,通过Arzela-Ascoli定理,我们知 为全连续算子。
为全连续算子。
引理2.2:函数
是三点边值问题(1.1)的正解,当且仅当
是算子A在锥中的不动点。
引理2.3:如果算子
是全连续的,那么算子
是全连续的。
注2:根据f的连续性,
是全连续的,因此由引理2.2知,算
也是全连续的。
引理2.4:如果u是T的不动点,那么u也是A的不动点。
证明:假设u是T的不动点,则对
,
,u也是A的不动点。
为此,我们只需要证如果
,那么
反之,如果
,使得 。令
为包含
点且使得
。令
为包含
点且使得
 的最大区间,则
,从而
的最大区间,则
,从而
1)
。
若
,则
,且
,而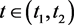 时,
,即
在
上为凹函数,所以
。但又
时,
,即
在
上为凹函数,所以
。但又
可知
由此得出矛盾。
若
,此时
 ,且
,且
 ,故
,故
由此也得出矛盾。
2)
。
若
,则
,且
于是
 ,
,
。
所以,
矛盾。
若
,则
,于是
从而
单调递减,而我们知
,从而
。这与
矛盾。
引理2.5 [5] (Leggett-Williams三解定理):设
 是全连续的,
a
是P上的一个非负连续凹泛函,满足当
时,
,假设存在
,使得
是全连续的,
a
是P上的一个非负连续凹泛函,满足当
时,
,假设存在
,使得
(C1) 当
,且
时,恒有
;
(C2) 当
时,恒有
;
(C3) 当
且
时,恒有
,
则A至少有三个不动点
,满足:
引理2.6 [6] :令X为一实Banach空间,其上的范数为
,
为两个锥,且
。假设
为两个全连续算子,且
为一连续泛函,满足对任意
,有
,其中
是一个常数。若存在常数
,使得
(M1)
;
(M2)
,且
;
(M3)
,
则T在K中至少有两个不动点
,满足
3. 主要结果
定理3.1:假设条件(H1)、(H2)、(H3)成立,又设存在正数
满足
,且使得f满足如下假设:
(H4)
;
(H5)
;
(H6)
;
(H7)
;
(H8)
;
(H9)
,
则边值问题(1.1)至少存在两个正解
满足
证明:对任意
,
由假设(H5)、(H7)有
故引理2.6中条件(M1)满足。
对任意
,即
,由假设(H5)、(H7)有
对
,即
,且
,我们有
所以
而
即
由假设(H6)、(H8)有
从而
。
另一方面,由引理2.1知,
故
引理2.6中条件(M2)满足。
最后,我们证明定理中的条件(M3)满足。
对
,即
,且
。
另一方面,
故
得
所以
由假设(H9)知,
通过假设(H4),我们有
从而
综上,引理2.6中的条件全部满足,则T有两个不动点
满足
再由引理2.4知,
为A的不动点,从而边值问题(1.1)至少存在两个正解。证毕。
定理3.2:假设(H1)~(H4)成立,又设
(
) 存在正数
满足
,使得
(
)
;
(
)
;
(
)
;
(
)
,
则边值问题(1.1)至少存在三个正解。
证明:定义非负连续凹泛函
,
显然,任取
,
。
又若
,有
且
。由假设(
)、(
)有
故
下面验证引理2.5中的条件(C1)~(C3)。
1) 取
,
t∈[0.1],
故
且任取
,即
所以,由假设(
)、(
)有
所以,引理中的条件(C1)满足。
2) 对 ,由假设(
)、(
)有
,由假设(
)、(
)有

所以,引理中的条件(C2)满足。
3) 取
,且
,则
所以,引理中的条件(C3)满足。
由Leggett-Williams三解定理,T至少有三个不动点
,且满足
再由引理2.4知,
为A的不动点,从而边值问题(1.1)至少存在三个正解。证毕。
文章引用
朱应丽,于秀洁. 一类非局部边值问题正解的存在性
The Existence of Positive Solutions for a Nonlocal Boundary Value Problem[J]. 应用数学进展, 2018, 07(08): 1085-1094. https://doi.org/10.12677/AAM.2018.78126
参考文献
- 1. Guidotti, P. and Merino, S. (2000) Gradual Loss of Positivity and Hidden Invariant Cones in a Scalar Heat Equation. Differential Integral Equations, 13, 1551-1568.
- 2. Infante, G. and Webb, J.R.L. (2006) Loss of Positivity in a Nonlinear Scalar Heat Equation. NoDEA Nonlinear Differential Equations Applications, 13, 249-261. https://doi.org/10.1007/s00030-005-0039-y
- 3. Webb, J.R.L. (2012) Existence of Positive Solutions for a Thermostat Model. Nonlinear Analysis: Real World Applications, 13, 923-938. https://doi.org/10.1016/j.nonrwa.2011.08.027
- 4. Infante, G. (2015) Nontrival Solutions of Local and Nonlocal Neumann Boun-dary Value Problems. Classical Analysis and ODEs.
- 5. Leggett, R. and Williams, L. (1979) Multiple Positive Fixed Points of Nonlinear Operators on Ordered Banach Spaces. Indiana University Mathematics Journal, 28, 673-688. https://doi.org/10.1512/iumj.1979.28.28046
- 6. Ge, W.G. and Ren, J.L. (2006) Fixed Point Theorems in Double Cones and Their Applications to Non-Linear Boundary Value Problems. Chinese Annals of Mathematics, 27, 155-168.






 时是绝缘的,加热或冷却操作是在
处的控制器根据传感器所反馈回的
t=0
时的温度来进行的。
时是绝缘的,加热或冷却操作是在
处的控制器根据传感器所反馈回的
t=0
时的温度来进行的。 ,则
。
,则
。 为全连续算子。
为全连续算子。 。令
为包含
点且使得
。令
为包含
点且使得
 的最大区间,则
,从而
的最大区间,则
,从而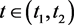 时,
,即
在
上为凹函数,所以
。但又
时,
,即
在
上为凹函数,所以
。但又 ,且
,且
 ,故
,故 ,
, 是全连续的,
a
是P上的一个非负连续凹泛函,满足当
时,
,假设存在
,使得
是全连续的,
a
是P上的一个非负连续凹泛函,满足当
时,
,假设存在
,使得 ,由假设(
)、(
)有
,由假设(
)、(
)有