Advances in Applied Mathematics
Vol.
09
No.
12
(
2020
), Article ID:
39439
,
8
pages
10.12677/AAM.2020.912257
基于快速正弦离散变换的有限差分方法求解半线性抛物型方程
刘昊,张荣培*,霍俊蓉
沈阳师范大学,辽宁 沈阳

收稿日期:2020年11月21日;录用日期:2020年12月20日;发布日期:2020年12月28日

摘要
针对带有Dirichlet边界条件的二维半线性抛物方程给出二阶中心差分格式,利用Kronecker积写出二维拉普拉斯算子的微分矩阵。进而应用Crank-Nicolson方法进行时间离散,采用Picard迭代求解离散得到的非线性代数方程组。具体实现过程中结合快速离散正弦变换,本文方法的优点是减少了存储量并大幅度降低了计算时间。数值算例验证本文的方法可以更好地捕捉解的爆破现象。
关键词
半线性抛物型方程,有限差分,Crank-Nicolson方法,离散正弦变换,爆破
Finite Difference Method for Solving Semi Linear Parabolic Equations Based on Fast Discrete Sine Transform
Hao Liu, Rongpei Zhang*, Junrong Huo
School of Mathematics and Systematic Sciences, Shenyang Normal University, Shenyang Liaoning

Received: Nov. 21st, 2020; accepted: Dec. 20th, 2020; published: Dec. 28th, 2020

ABSTRACT
In this paper, the second-order finite difference scheme is applied for the numerical solution of the two-dimensional semi-linear parabolic equations with Dirichlet boundary conditions. We construct the differentiation matrix of two-dimensional Laplacian operator by Kronecker product. The time discretization method is chosen as Crank-Nicolson method. In every time level we solve the nonlinear algebraic equations by Picard iteration method. The fast discrete Sine transform is applied in the process of implementation. The major feature of the proposed method is that the memory requirement and CPU time are reduced obviously. Numerical examples show that the proposed method can better capture the blow up phenomenon of the solution.
Keywords:Semi-Linear Parabolic Equation, Finite Difference, Crank-Nicolson Method, Discrete Sine Transform, Blow-Up

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
半线性抛物与线性抛物方程的一个重要区别在于,随着时间发展其解具有奇异性。也就是说,尽管初始值是光滑的,但是在某个时间点T,方程的解也可能会趋向于无穷大,这种解的奇异性称之为爆破,T称之为爆破时间点。在本文中,我们考虑求解如下半线性抛物型方程:
(1)
边界和初始条件如下:
(2)
其中, , 的常数, 为一个矩形区域, 代表边界, 为初始值。关于方程(1)的爆破解有许多学者进行了研究 [1],文献 [2] 给出了下面的定理:
定理1:令 ,如果 , 是问题的临界指数。对于(1)的任何非平凡解,存在一个爆破时间T,
方程(1)在核反应动力学、奇异摄动问题等方面有广泛的应用 [3]。由于右端非线性项的存在,很难得到精确解,所以关于该问题数值解的研究具有非常重要的意义。近年来众多学者发展了丰富的数值方法求解该方程。F. De La Hoz等人提出了谱方法和指数时间差分法 [4];王俊俊等人发展了混合有限元方法 [5];张荣培等人将Chebyshev谱方法应用于求解此类方程 [6];Ju等人发展了紧致指数积分因子法 [7];熊之光等人提出了高效有限体积元法 [8]。但上述方法在求解过程中需要求解大型的非线性代数方程组,计算复杂,耗费时间较多。本文应用Kronecker积的性质将二维拉普拉斯算子的微分矩阵进行特征分解,结合快速正弦离散变换方法,节省了计算时间。
本文框架如下:第一部分给出半线性抛物方程的有限差分格式,应用Kronecker积写出二维拉普拉斯算子的微分矩阵K,时间离散上采用Crank-Nicolson方法。第二部分给出实现过程,应用Kronecker积的性质将微分矩阵K进行特征分解,结合快速正弦离散变换方法求解矩阵与向量的乘积,使得计算时间和内存大幅度减少。最后给出数值算例,验证本文给出的方法可以更加精确地捕捉爆破解。
2. 有限差分格式
首先用直线 , 在 上打网格,其中网格节点为 ,,,,网格步长为 ,。设u在网格节点 的数值解为 ,由Dirichlet边界条件,在网格内部点 采用二阶中心差分格式:
(3)
定义离散解的矩阵U为:
定义如下差分方程的微分矩阵为 :
其中, 。
设 分别为 阶单位矩阵,将解矩阵向量化后得
(4)
利用(3)式以及Kronecker积的定义,(1)式的二阶中心差分格式可以写成矩阵形式
(5)
其中 , 表示对 每个元素做运算。
计算终止时间为T,时间步长 ,则第n层时间步长 。接下来应用Crank-Nicolson格式对(5)式进行求解,
(6)
其中 ,是拉普拉斯算子的微分矩阵。上式等价于
(7)
下面采用Picard迭代求解非线性代数方程组
(8)
具体的Picard迭代算法如下:
上述算法可分为内循环和外循环,外循环 是关于时间的循环, 为内循环,当 时,跳出内循环,外循环一直计算到时间终止。
3. 快速求解
在式(7)中需要求矩阵 以及 与向量的乘积,两个矩阵乘积的运算相似,下面以 为例进行说明。为了快速计算,首先将矩阵K进行分解。下面给出两个定理。
定理2:矩阵 进行对角化,定义对角矩阵 ,,,则 ,即
(9)
其中 。
矩阵 为离散正弦变换矩阵,是一个正交矩阵,即 ,在Matlab中可以由命令dst(N)生成。该定理证明参考文献 [9]。对 也可得类似的结果。
定理3:Kronecker积的性质 [9]:
1)
2)
3)
4)
5)
接下来利用定理2和3对矩阵K进行特征分解,由 ,利用定理3性质1和性质2可得:
(10)
对 可做类似运算。有下式成立
(11)
这里 是一个对角矩阵。
定义矩阵
则易证明
(12)
根据矩阵K的分解,可得下面的分解
(13)
基于上述矩阵可分解性质,下面分三步利用利用快速正弦变换完成矩阵与向量乘积的运算实现 。
Step1
(14)
Step2
定义 ,其中 ,则由(12)可得 ,从而
(15)
其中 为矩阵中每个元素相乘。
Step3
(16)
注:Step1中,在Matlab中利用 实现;Step3中,在Matlab中利用 实现。
4. 数值实验
应用本文提出的有限差分法求解下面的数值算例。考虑二维计算区域 ,针对具有齐次狄利克雷边界条件的方程(1)进行求解。网格剖分128 × 128,时间离散步长时间步长 ,因为临界指数 ,所以在数值实验中选择 ,对不同的时间点t进行数值模拟。
情形1. 初值选取为 。三个时间点 ,, 的计算结果在图1中列出。初始条件在原点峰值为10,t取如图1中的各值时,可以看到随着时间的进行,单峰图像逐渐变陡,向原点不断聚拢,最终在 达到爆破的峰值 。
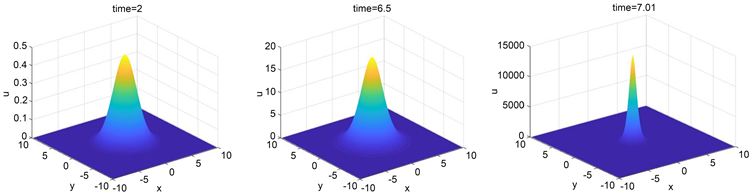
Figure 1. The numerical simulation results of case 1 when ,,
图1. 情形1在计算时间 ,, 下的数值模拟结果
情形2. 初值选取 ,其他参数与情形1相同,三个时间点 ,, 的计算结果如图2所示。初始条件在原点的峰值为10,从图像可以看出它们是关于原点对称的,随着时间的进行,双峰逐渐聚合,在 时效果较为明显,在 时爆破值达到4 × 104。
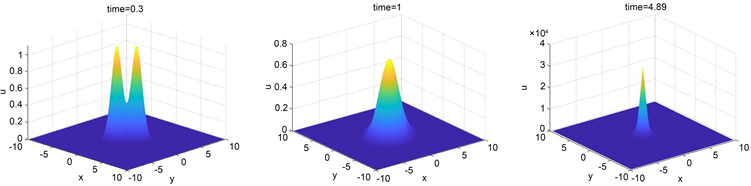
Figure 2. The numerical simulation results of case 2 when ,,
图2. 情形2在计算时间 ,, 下的数值模拟结果
情形3. 初值选取
其他参数与情形2相同,三个时间点 ,, 的计算结果如图3所示。初始条件的峰值为10。可以发现随着时间的进行,四个峰的聚拢方向依然指向原点,最后实现爆破。这三个实验的结果非常相似,无论初值有多少极值点,在一定的时间过程后,最终都会向原点聚拢,进而达到爆破的结果。数值模拟结果验证了定理1的理论。
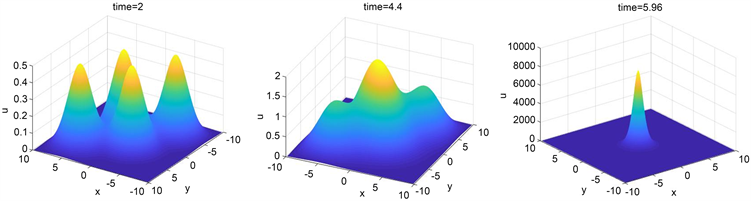
Figure 3. The numerical simulation results of case 3 when ,,
图3. 情形3在计算时间 ,, 下的数值模拟结果
为了显示本文方法计算速度快的优点,表1给出使用快速离散正弦变换和不使用快速离散正弦变换计算式(6)的时间比较。从表1可以发现,不使用快速离散正弦变换的计算时间较长,而应用本文的数值方法进行模拟的运行时间大大减少。
Table 1. Time comparison of three cases of DST and No DST
表1. 三种情形下使用速离散正弦变换和不使用速离散正弦变换的时间比较
5. 总结
本文应用快速离散正弦变换求解半线性抛物线型方程,该方法能够快速地求解离散后得到的非线性代数方程组,提高了计算效率。通过求解齐次狄利克雷边界条件下的半线性抛物线型方程,可以发现随时间推移数值结果形状的变化规律,即在一定时间后,数值解发生了爆破。在本文问题求解的过程中,当 时,当利用高斯消去法解代数方程组时,计算复杂度高达 ,但通过本文所应用的快速离散正弦变换方法,复杂度仅有 ,大大降低了算法的复杂度,使得程序运算时间明显缩短。下一步的工作是将该方法推广至求解四阶的抛物线型方程。
文章引用
刘 昊,张荣培,霍俊蓉. 基于快速正弦离散变换的有限差分方法求解半线性抛物型方程
Finite Difference Method for Solving Semi Linear Parabolic Equations Based on Fast Discrete Sine Transform[J]. 应用数学进展, 2020, 09(12): 2209-2216. https://doi.org/10.12677/AAM.2020.912257
参考文献
- 1. 张亮, 李建军. 一类半线性抛物方程的解的爆破性质研究[J]. 应用数学进展, 2017, 6(1): 10-19.
- 2. Francisco, D.L.H. and Vadillo, F. (2013) A Sylvester-Based IMEX Method via Differentiation Matrices for Solving Nonlinear Parabolic Equations. Communications in Computational Physics, 14, 1001-1026. https://doi.org/10.4208/cicp.050612.180113a
- 3. 王明新, 顾永耕. 核反应动力学中的一个半线性抛物型方程组[J]. 科学通报, 1994(3): 193-193.
- 4. Hoz, F.D.L. and Vadillo, F. (2009) A Numerical Simulation for the Blow-Up of Semi-Linear Diffusion Equations. International Journal of Computer Mathematics, 86, 493-502. https://doi.org/10.1080/00207160701627161
- 5. 王俊俊, 郭丽娟. 一类半线性抛物型方程混合有限元法的超逼近分析[J]. 应用数学, 2019, 32(1): 71-80.
- 6. 张荣培, 刘佳, 王语. Chebyshev谱配置方法求解Allen-Cahn方程[J]. 沈阳师范大学学报(自然科学版), 2017(35): 440.
- 7. Ju, L., Zhang, J., Zhu, L., et al. (2015) Fast Explicit Integration Factor Methods for Semi-Linear Parabolic Equations. Journal of Scientific Computing, 62, 431-455. https://doi.org/10.1007/s10915-014-9862-9
- 8. 熊之光, 王易, 马娟. 半线性抛物问题高效有限体积元法[J]. 理论数学, 2019, 9(8): 961-968.
- 9. Strang, G. (2007) Computational Science and Engineering. Wellesly-Cambridge Press, MA.
NOTES
*通讯作者。
