Computer Science and Application
Vol.
13
No.
05
(
2023
), Article ID:
66221
,
9
pages
10.12677/CSA.2023.135105
区间值决策系统下最短约简算法的研究
贾凯文
烟台大学计算机与控制工程学院,山东 烟台
收稿日期:2023年4月22日;录用日期:2023年5月22日;发布日期:2023年5月30日

摘要
属性约简可以选出保持分类能力不变的属性子集,而最短约简不仅可以选出保持分类能力不变的属性子集,还可以最大程度地删除冗余属性、压缩决策表,选出最优的属性子集。本文在区间值决策系统的数据背景下,分别对针对决策属性的全部决策类和特定决策类构建二进制差别矩阵,结合SRA算法分别提出了基于二进制差别矩阵的最短约简算法和特定类最短约简算法。为了验证算法的有效性,选取8组UCI数据集分别从算法的约简结果长度和约简效率两方面进行对比,实验结果证明了算法的可行性和有效性。
关键词
粗糙集,最短约简,二进制差别矩阵,区间值决策系统

Research on Shortest Reduction Algorithm in Interval-Valued Systems
Kaiwen Jia
School of Computer and Control Engineering, Yantai University, Yantai Shandong
Received: Apr. 22nd, 2023; accepted: May 22nd, 2023; published: May 30th, 2023

ABSTRACT
Attribute reduction can select a subset of attributes that maintains the classification ability, while shortest reduction can not only select a subset of attributes that maintains the classification ability, but also delete redundant attributes and compress decision tables to select the optimal subset of attributes. In this paper, based on the data background of interval-valued decision systems, binary discernibility matrix were constructed for all decision classes and specific decision classes, and the shortest reduction algorithm and the specific class shortest reduction algorithm based on binary discernibility matrix were proposed, respectively, combined with the SRA algorithm. To verify the effectiveness of the algorithm, 8 UCI datasets were selected for comparison from the perspective of the length of the reduction result and the efficiency of the reduction algorithm. The experimental results prove the feasibility and effectiveness of the algorithm.
Keywords:Rough Set, Shortest Reduction, Binary Discernibility Matrix, Interval-Valued Decision Systems

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
粗糙集理论 [1] 是一种分析数据,获取知识的有效工具之一,通过将原始数据中冗余和无关的属性进行剔除,从而降低数据的维度。属性约简 [2] [3] 是粗糙集理论的一个重要概念和研究方向。属性约简可以选出保持分类能力不变的属性子集,而最短约简 [4] 不仅可以选出保持分类能力不变的属性子集,还可以最大程度地删除冗余属性、压缩决策表,选出最优的属性子集。因此,最短约简问题也是粗糙集领域的一个热点问题,诸多学者从不同角度对最短约简做了大量的研究。Lv等 [5] 改进了遗传算法,从量子遗传算法的角度和区分表结合解决最短约简问题,但是计算过程中需要不断调整参数,并且量子位很容易受到外部环境的影响;Zhou等 [6] 使用差别矩阵方法,揭示了属性约简中不同目标函数之间的关系,进一步从差别函数的角度解决最短约简问题,但是属性重要度的计算需要花费较高计算成本;Rodriguez-Diez等 [7] 从二进制差别矩阵的角度解决最短约简问题,使用二进制累积运算和快速的候选属性评估过程,并给出了相应算法,但是矩阵密度的大小会影响算法的效率;Gonzalez-Diaz等 [8] 在二进制差别矩阵提出了求取最短约简的方法,基于属性贡献度的概念,该方法首先找到决策表最短约简的大小,通过缩小搜索空间进一步计算决策表的所有最短约简,但是只适用于经典的决策系统。
对最短约简问题的研究大多是在二进制差别矩阵 [9] [10] 上进行的。Yao等 [11] 通过经典高斯消除的方式简化二进制差别矩阵,并提出了两种启发式方法计算属性约简;Lazo-Cortes等 [12] 基于简化的二进制差别矩阵,通过减小搜索空间提出了计算属性约简的MSLC算法;Zhang等 [13] 通过构造确定性有限自动机来快速比较不同行和列之间的关系,在此基础上提出了简化二进制差别矩阵的快速算法。
基于上述讨论,差别矩阵可以一次性求取全部属性约简,但是算法的复杂度较高,且有时无法输出全部的约简结果。现有的最短约简工作虽然大多基于二进制差别矩阵方法,但是只适用于经典的粗糙集系统,并且对决策属性的全部决策类进行属性约简,没有针对性。本文在区间值决策系统的数据背景下,分别对针对决策属性的全部决策类和特定决策类构建二进制差别矩阵,结合SRA算法分别提出了两种最短约简算法。为了验证算法的有效性,选取了8组UCI数据集对算法进行验证,分别从算法的约简结果长度和约简效率两方面进行对比,最后通过实验证明了算法的可行性和有效性。
2. 基本概念
四元组 为区间值决策系统, 为非空论域有限对象的集合, 是非空有限属性的集合, 是决策属性集合,且 ; , 为条件属性值集合, 为决策属性值集合; 为条件属性信息函数, 为决策属性信息函数。 表示对象 在属性 上的取值,记为 。 表示在属性 下对象 的取值,其中, 和 分别表示该区间值数据的左边界和右边界。表1所示为区间值决策系统对应的区间值决策表,其中,论域 ,条件属性集合 ,决策属性集合 。
Table 1. Interval-valued decision systems
表1. 区间值决策表
定义1. [14] 给定区间值决策系统 , , , 和 两个对象在条件属性 下的Jaccard相似率 定义为:
,
其中: 表示数据区间的长度。Jaccard相似率用于度量两个区间值数据之间的相似程度。
定义2. [15] 给定区间值决策系统 , , , , ,则关于条件属性集E的 -相容关系为:
。
对于 ,对象 在条件属性E下的 -相容类为:
。
关于区间值决策系统IVDS的 -相容类集合为:
。
由等价关系产生的等价类集合构成了对论域的划分;由相容关系产生的相容类集合构成了对论域的覆盖。
定义3. [16] 给定区间值决策系统 ,对于 , , , , , 表示对象 的相容类,集合B关于条件属性集合E的上、下近似集合定义为:
,
。
决策类集合S/D关于条件属性E的正域定义为:
。
3. 区间值决策系统下的最短约简
定义4. 设四元组 为一个区间值决策系统,论域集合为 ,条件属性集合为 ,决策属性集合为 , , , ,正域保持约简对应的二进制差别矩阵为 ,其中 为对象 和对象 在属性 下的比较结果, 的表示如下:
,
其中: 。矩阵中的行为对象对,列为属性,如果对象对 在属性 下满足 ,则元素 值为1;否则,值为0。
定义5. 给定区间值决策系统 ,二进制差别矩阵 , ,若属性子集E满足:
1) 对于任意 ,存在 ,使得 ,
2) 对于任意 , ,存在 ,使得 。
则称属性子集E为区间值决策系统IVDS的正域保持约简。其中,1) 为联合充分性条件;2) 为个体必要性条件。若属性子集E只满足条件(1),则称属性子集E为超约简。
定义6. [10] 给定区间值决策系统 ,二进制差别矩阵为 ,简化的二进制差别矩阵 通过如下方式由 得到:
1) 首先去掉二进制差别矩阵 中全为0的行;
2) 在变换过程中,随时去掉二进制差别矩阵 中全为1的行;
3) 将二进制差别矩阵 中的行、列重新排序,去掉二进制差别矩阵 中重复的行;
4) 对于 ,若 列与 列存在 的关系,则去掉 列;
5) 对于 ,若 行与 行存在 的关系,则去掉 行。
经过上述变换之后,二进制差别矩阵的规模大大减小,文献 [11] 已证明新的矩阵包含和原矩阵包含相同的约简结果,简化的二进制差别矩阵 是 消除了多余和重复行之后的简化版本。
Table 2. Shortest reduction algorithm based on Binary Discernibility Matrix (IVSRA)
表2. 基于二进制差别矩阵的最短约简算法
基于上述内容,构造出在区间值决策系统下基于全部决策类的二进制差别矩阵,再将SRA算法引入其中,在此基础上提出了基于二进制差别矩阵的最短约简算法,具体描述如表2所示。
4. 区间值决策系统下特定类的最短约简
定义7. 给定区间值决策系统为 , 为论域的集合,
为条件属性的集合, 为决策属性的集合,决策属性的划分为 , , , , ,针对特定决策类集合P基于正域保持约简对应的二进制
差别矩阵为 ,其中 为对象 和对象 在属性 下的比较结果, 定义如下:
,
其中: 。如果对象对 在 下满足 ,则元素 值为1;否则,值为0。
定义8. 给定区间值决策系统 ,二进制差别矩阵 , ,若属性子集E满足下述条件,则称属性子集E为特定决策类集合P的正域保持约简。
1) 对于 ,存在 ,使得 ,
2) 对于 , , ,使得 。
其中:1) 为联合充分性条件,2) 为个体必要性条件。
基于上述讨论,提出了基于二进制差别矩阵的特定类最短约简算法,具体描述如表3所示。
Table 3. Specific-class shortest reduction algorithm based on Binary Discernibility Matrix (IVLSRA)
表3. 基于二进制差别矩阵的特定类最短约简算法
5. 实验分析
本节对所提出的IVSRA算法和IVLSRA算法进行验证,实验从两个角度对算法进行了比较:1) 最短约简长度;2) 约简效率。实验选取8组UCI数据集(https://archive.ics.uci.edu/ml/datasets.php),表4提供了数据集的具体信息。实验环境采用Inter Core i3-9100H (3.60 GHz)处理器、8 GB内存、Windows10 64位操作系统,采用的编程语言为Python,在PyCharm2020上编译运行。
Table 4. UCI datasets
表4. UCI数据集
5.1. 约简长度对比
本小节对使用二进制差别矩阵求取最短约简的IVSRA算法、针对特定决策类的IVLSRA算法与使用经典构造差别矩阵方法的PDM算法进行约简结果最短长度的比较,如表5所示。IVSRA算法与PDM算法得到的最短约简长度是一致的,IVSRA算法不仅可以求出数据集的所有最短约简结果而且时间耗时更短。针对特定决策类的IVLSRA算法得到的最短约简长度短于PDM算法和IVSRA算法得到的最短约简长度。实验结果说明本文所提IVSRA算法能够以更快的时间得到更少数量的最短约简结果,针对特定类的IVLSRA算法能够得到更短的最短约简结果,人为选取特定类会使结果更有针对性,且能提高效率。
Table 5. The length of shortest reduct
表5. 最短约简长度
5.2. 约简长度对比
图1展示了IVSRA和IVLSRA算法的约简效率对比,图中横坐标表示条件属性的数量,纵坐标表示算法的运行时间,单位为秒。由图1(a)~(h)可知,随着属性数量的增加,PDM算法求取属性约简消耗的时间增加越来越快,所提IVSRA算法求取最短属性约简的时间较为平缓。IVLSRA算法的时间消耗速度比PDM算法和IVSRA算法都缓慢。当属性全部添加时,IVSRA算法的时间消耗小于PDM算法的时间消耗,针对特定类的IVLSRA算法的时间消耗远小于IVSRA算法的时间消耗。实验说明IVSRA算法的计算效率优于PDM算法的计算效率,针对特定决策类的IVLSRA算法的时间效率远远高于IVSRA算法和PDM算法的时间效率,IVSRA算法和IVLSRA算法通过二进制的形式高速构建差别矩阵以及高效的求取最短约简算法,从而提高了算法整体的效率。
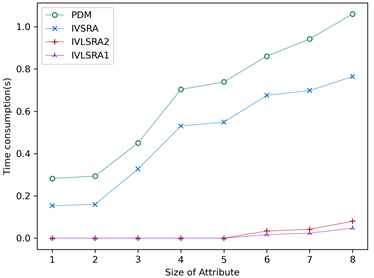 (a) Aquatic Toxicity
(a) Aquatic Toxicity
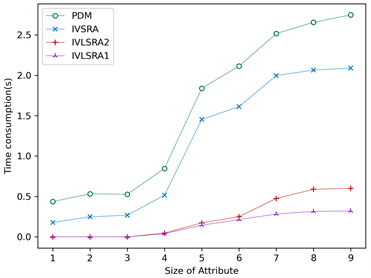 (b) Bioconcentration
(b) Bioconcentration
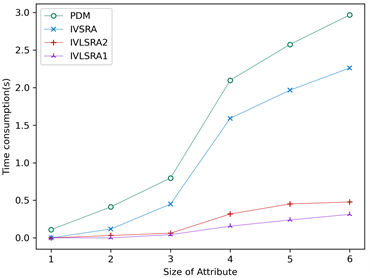 (c) Fish Toxicity
(c) Fish Toxicity
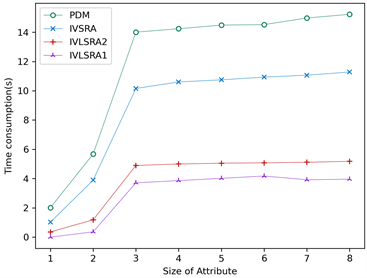 (d) Yeast
(d) Yeast
 (e) Wine Quality-red
(e) Wine Quality-red
 (f) Cardiotocography
(f) Cardiotocography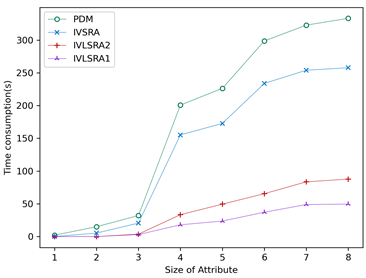 (g) Abalone
(g) Abalone
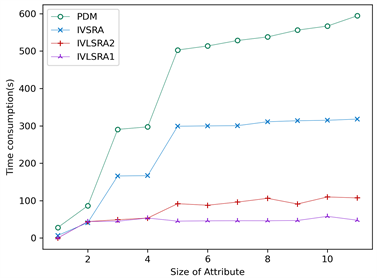 (h) Wine Quality-white
(h) Wine Quality-white
Figure 1. Comparison of reduction efficiency of algorithm IVSRA and IVLSRA
图1. IVSRA和IVLSRA算法约简效率对比
6. 总结
本章构建了以区间值决策系统为数据背景的二进制差别矩阵和针对特定决策类的二进制差别矩阵,给出了区间值决策系统下二进制差别矩阵的定义,结合SRA算法求取区间值决策系统下针对全类和特定类的最短约简,实验使用8组UCI数据集分别比较了最短约简长度和约简效率,实验证明了算法的高效性和稳定性。下一步将在决策属性多层次系统下研究最短约简。
基金项目
本文受烟台市科技计划项目(编号:2022XDRH016)的资助。
文章引用
贾凯文. 区间值决策系统下最短约简算法的研究
Research on Shortest Reduction Algorithm in Interval-Valued Systems[J]. 计算机科学与应用, 2023, 13(05): 1074-1082. https://doi.org/10.12677/CSA.2023.135105
参考文献
- 1. Pawlak, Z. (1982) Rough Sets. International Journal of Computer and Information Sciences, 11, 341-356. https://doi.org/10.1007/BF01001956
- 2. 苗夺谦, 胡桂荣. 知识约简的一种启发式算法[J]. 计算机研究与发展, 1999, 36(6): 681-684.
- 3. Wang, C.Z., Huang, Y., Ding, W.P. and Cao, Z.H. (2021) Attribute Reduction with Fuzzy Rough Self-Information Measures. Information Sciences, 549, 68-86. https://doi.org/10.1016/j.ins.2020.11.021
- 4. Lin, T.Y. and Yin, P. (2004) Heuristically Fast Finding of the Shortest Reducts. 4th International Conference, RSCTC 2004, Uppsala, 1-5 June 2004, 465-470. https://doi.org/10.1007/978-3-540-25929-9_55
- 5. Lv, Y.J. and Liu, N.X. (2007) Application of Quantum Genetic Algorithm on Finding Minimal Reduct. IEEE International Conference on Granular Computing (GRC 2007), San Jose, 2-4 November 2007, 725-728. https://doi.org/10.1109/GrC.2007.87
- 6. Zhou, J., Miao, D.Q., Feng, Q.R. and Sun, L.J. (2009) Research on Complete Algorithms for Minimal Attribute Reduction. 4th International Conference, RSKT 2009, Gold Coast, 14-16 July 2009, 152-159. https://doi.org/10.1007/978-3-642-02962-2_19
- 7. Rodriguez-Diez, V., Martinez-Trinidad. J.F., Carras-co-Ochoa, J.A., Lazo-Cortes, M.S. and Olvera-Lopez, J.A. (2020) MinReduct: A New Algorithm for Computing the Shortest Reducts. Pattern Recognition Letters, 138, 177-184. https://doi.org/10.1016/j.patrec.2020.07.004
- 8. Gonzalez-Diaz, Y., Martinez-Trinidad, J.F., Carrasco-Ochoa, J.A. and Lazo-Cortes, M.S. (2022) Algorithm for Computing All the Shortest Reducts Based on a New Pruning Strategy. Information Sciences, 585, 113-126. https://doi.org/10.1016/j.ins.2021.11.037
- 9. Felix, R. and Ushio, T. (1999) Rough Sets-Based Machine Learning Using a Binary Discernibility Matrix. Proceedings of the 2nd International Conference on Intelligent Processing and Manufacturing of Materials, Honolulu, 10-15 July 1999, 299-305. https://doi.org/10.1109/IPMM.1999.792493
- 10. 支天云, 苗夺谦. 二进制可辨矩阵的变换及高效属性约简算法的构造[J]. 计算机科学, 2002, 29(2): 140-142, F004.
- 11. Yao, Y.Y. and Zhao, Y. (2009) Discernibility Matrix Simplification for Constructing Attribute Reducts. Information Sciences, 179, 867-882. https://doi.org/10.1016/j.ins.2008.11.020
- 12. Lazo-Cortes, M.S., Martinez-Trinidad, J.F., Carrasco-Ochoa, J.A. and Diaz, G.S. (2016) A New Algorithm for Computing Reducts Based on the Binary Discernibility Matrix. Intelligent Data Analysis, 20, 317-337. https://doi.org/10.3233/IDA-160807
- 13. Zhang, N., Li, B.Z., Zhang, Z.X. and Guo, Y.Y. (2018) A Quick Algorithm for Binary Discernibility Matrix Simplification Using Deterministic Finite Automata. Information, 9, Ar-ticle No. 314. https://doi.org/10.3390/info9120314
- 14. 刘鹏惠, 陈子春, 秦克云. 区间值信息系统的决策属性约简[J]. 计算机工程与应用, 2009, 45(28): 148-150, 229.
- 15. Leung, Y., Fischer, M.M., Wu, W.Z. and Mi, J.S. (2008) A Rough Set Approach for the Discovery of Classification Rules in Interval-Valued Information Systems. International Journal of Approximate Reasoning, 47, 233-246. https://doi.org/10.1016/j.ijar.2007.05.001
- 16. 张楠, 苗夺谦, 岳晓冬. 区间值信息系统的知识约简[J]. 计算机研究与发展, 2010, 47(8): 1362-1371.
