基于线性规划下的机器人最优避障路径模型 Optimal Obstacle Avoidance Path Model for Robots Based on Linear Programming

doi:10.12677/MOS.2022.114099

Modeling and Simulation
Vol. 11 No. 04 ( 2022 ), Article ID: 53733 , 13 pages
10.12677/MOS.2022.114099

基于线性规划下的机器人最优避障路径模型

王梦甜，张巍，陈晓友^*

●How to Cite this Article

河南工业大学理学院，河南郑州

收稿日期：2022年5月5日；录用日期：2022年7月7日；发布日期：2022年7月18日

摘要

近年来随着科技的快速发展，机器人技术被广泛地应用于家庭服务、工业指导、军事作业等多个领域。本文运用栅格建模以及线性规划模型，建立了机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型。其中最短路径模型给出了机器人行走的原则，为机器人可能路径的选择提供了依据，同时讨论了行走路径中机器人直线段长度和弧线段长度的计算方法，以及直线与圆弧切点坐标的计算方法，为后续问题的解决提供了很好的工具；最短时间模型以行走时间最短为目标，找出了最合适的转弯圆心和半径，然后通过建立线性规划模型求得了最优解。

关键词

线性规划，栅格建模，旅行商(TSP)问题，MATLAB

Optimal Obstacle Avoidance Path Model for Robots Based on Linear Programming

Mengtian Wang, Wei Zhang, Xiaoyou Chen^*

School of Sciences, Henan University of Technology, Zhengzhou Henan

Received: May 5^th, 2022; accepted: Jul. 7^th, 2022; published: Jul. 18^th, 2022

ABSTRACT

With the rapid development of technology in recent years, robotics is widely used in many fields such as home services, industrial guidance, and military operations. This paper uses raster modeling and linear programming model to establish the mathematical models of the shortest path and the shortest time path for the robot to avoid obstacles from one point in the region to another point—the shortest path model gives the principles of robot walking and provides the basis for the selection of possible paths for the robot; it also discusses the calculation methods of the lengths of the straight-line and arc segments of the robot in the walking path, as well as the coordinates of the tangent points of the straight line and the arc, which provides a good tool for solving follow-up problems; the shortest time model takes the shortest walking time as the goal, finds out the most suitable turning circle center and radius, and then finds the optimal solution by establishing a linear programming model.

Keywords:Linear Programming, Raster Modeling, Travel Merchant (TSP) Problems, MATLAB

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

近年来随着科技的快速发展，机器人技术被广泛地应用于家庭服务、工业指导、军事作业等多个领域，如工业智能机器人，他们在很多方面超越了传统机器人。伴随着越来越多的工作可以被机器人代替，机器人已经开始走进人们的日常生活中，如扫地机器人、物流机器人等。随着机器人的普及，如何在工作的时候尽量避开障碍以提高工作效率，逐渐得到关注，这也是决定机器人工作效能的一个重要指标。

机器人避障问题指的是机器人利用传感器识别前进路线上的障碍物，绕过或者跨越障碍物的问题。机器人行进过程中可以选择的路径有很多，但如何选择最短路径是现代科学领域的一个热点问题，也就是说如何合理地找到从起点到目标终点的最短路径并且不与障碍物发生碰撞。

迄今为止，国内外众多学者 [1] - [6] 已经提出了很多路径规划的算法，比如随机方法、单元分解法和神经网络算法等。文献 [3] 采用单元分解法进行路径规划，有效简化了计算，但是此法的实验结果往往与环境地图有关，较适用于一些简单的环境，具有一定的偶然性。文献 [4] 采用神经网络算法，此法能够应用于各种各样的环境并且能够规划出较好结果的路径，但需要巨大的运算量，对机器人的硬件设备要求较高。文献 [5] 使用随机方法，此法不需要进行环境地图建模，但是无法保障其稳定性，随机性较大。

为提高移动机器人避障路径的规划能力，本文提出基于线性规划下的移动机器人避障路径规划方法。基于相关案例，模拟在一定面积的室内，随机设置若干个不同类型的障碍物，通过设计算法并利用软件进行计算，给出机器人从某一点到另一点的避障最短路径以及最短时间的路径，为解决实际问题提供一定的参考。

2. 环境建模

根据实际情况，我们作一个800 × 400的平面场景图来模拟机器人的工作场景，以100作为栅格块的长度，随机设置若干个不同形状的障碍物并放入栅格地图中，如图1所示。

为便于计算，本文规定各点的位置坐标，即O (0, 0)，A (300, 300)，G (700, 100)。在栅格地图中，障碍物外指定一点为机器人要到达的目标点。通过调研分析实际情况中机器人的工作情形，现规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人的转弯路径。机器人不能折线转弯，转弯路径由直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但是每个圆弧的半径最小为10个单位。为了不与障碍物发生碰撞，同时要求机器人的行走路线与障碍物间的最近距离为10个单位，否则发生碰撞。若碰撞发生，则机器人无法完成行走。为了保障机器人行走过程中的平稳性，要求机器人的加速度不超过 $a_{0} = 1 m / s^{2}$ 。如果超过此加速度，机器人将发生前倾或后倒，无法完成行走。为减小计算量，本文规定机器人直线行走和转弯的速度为 $v_{0} = 5$ 个单位/秒，忽略从静止到加速的时间。机器人转弯时，最大转弯速度为

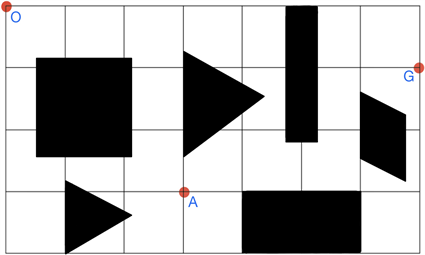
Figure 1. Planar scene view

图1. 平面场景图

$v (ρ) = \frac{v_{0}}{1 + e^{10 - 0.1 ρ^{2}}}$

其中𝜌是转弯半径。如果超过该速度，机器人将发生侧翻，无法完成行走。

根据以上假设，建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型，具体来说主要计算以下两个问题：

Q1：机器人从O (0, 0)出发，O→A的最短路径；

Q2：机器人从O (0, 0)出发，到达A的最短时间路径。

3. 模型的建立

3.1. 最短路径模型

机器人在行走时要求与障碍物间的最近距离为10个单位，因此可以先确定机器人可以行走的区域。但可行走区域是非常大的，机器人有很多种行走路径，于是需要确定机器人按怎样的原则行走才能保证路径最短。行走原则确定之后，需要解决的就是计算问题，需要考虑机器人直线段长度和弧线段长度的计算方法，以及直线与圆弧切点坐标的计算方法。这样才能解决最短路径的确定以及路径长度计算等一系列问题。

3.1.1. 机器人可行区域的确定

机器人在行进过程中与障碍物有最小距离限制。因此，本文先给出机器人的可行区域，便于问题的分析与求解。如图2所示，细黑线以外的蓝色区域为机器人的可行区域，机器人可以在此区域内任意行走。

3.1.2. 机器人行走原则的确定

1) 在障碍物顶点处拐弯使行走路径最短

如图3，从O点到A点，本文假设有OBA和OCA两条路线，分别在B点和C点转弯。从图形中明显可以看出OBA比OCA短，即靠近障碍物禁区边缘的转弯路径小。下面将进行证明。

Figure 2. Areas where the robot is feasible

图2. 机器人可行区域

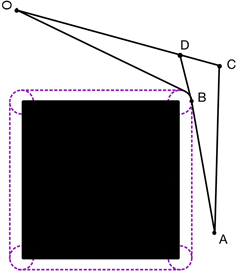
Figure 3. Different ways of turning

图3. 不同转弯方式

本文先不考虑机器人的转弯路径为圆弧，设B为禁区顶点，C为禁区外任意一点，延长AB交OC为D点。由三角形任意两边之和大于第三边可得：

$\begin{array}{l} A C + C D > A D, \\ O B + B D > O D, \end{array}$

两式相加可得：

$A C + C D + O D + B D > A D + O B,$

又因为

$\begin{array}{l} O C = O D + D C, \\ A D = A B + B D, \end{array}$

化简可得：

$A C + O C > A B + O B .$

即靠近禁区边缘转弯路径相对最短。因此，机器人要优先选择在障碍物顶点处转弯。

2) 转弯圆弧的半径为10使行走路径最短

如图4， $p_{1}, p_{2}$ 分别为小圆和大圆的半径 $(p_{1} < p_{2})$ ，B点为两圆内切时的公共切点，D、C点分别为小圆和大圆与对应直线的切点。

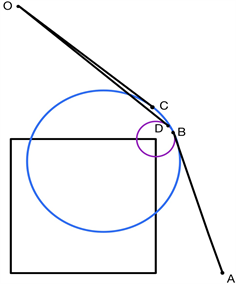
Figure 4. Different turning radius

图4. 不同转弯半径

由图明显可以看出，区域ODBA的面积小于区域OCBA的面积。同时，两个区域有公共边OA和AB，而且曲线OCB和曲线ODB都有向外凸的趋势。因此，根据覆盖法的思想，我们可以得到曲线ODB的长度小于曲线OCB。

所以，可以得到一个结论：转弯半径越小，路径相对越短。但机器人行走过程中需要距离障碍物最少10个单位，因此在Q₁中把转弯路径定为10。

3) 转弯圆弧的圆心在障碍物顶点处使行走路径最短

如图5，圆O₁、O₂是半径相等的圆。O₁为障碍物顶点，O₂为机器人可行区域中任意一点。过O点、A点分别作圆O₁、O₂的切线并延长相交于点C、B。由于区域OAB的面积明显大于区域OAC，且有公共边OA，同时两区域方向一致，皆为相外凸型。因此，根据覆盖法的思想，曲线OA的长度小于曲线OB。即转弯圆弧以障碍物顶点为圆心时，路径最短。

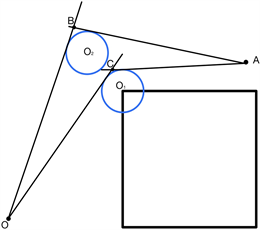
Figure 5. Different turning circles

图5. 不同转弯圆心

4) 以圆形障碍物禁区边缘为转弯圆弧处使行走路径最短

在题目所给平面图中有一个特殊的圆形障碍物，下面将证明上述结论在圆形障碍物中仍然适用。

如图6，机器人过圆形障碍物有三种方式。a图是以禁区边界为转弯路径；b图是以障碍物上一点为圆心，半径为10的圆弧为路径；c图是一个在禁区外转弯的路径。

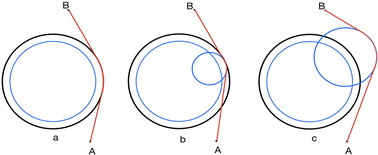
Figure 6. Three ways to cross a circular obstacle

图6. 过圆形障碍物的三种方式

由图可以看出，b图路径最短，但进入了禁区，因此排除b方法。而在a和c图中明显可以看出a图中路径更短一点。因此，机器人在圆形障碍物处仍然以禁区边缘为转弯路径。则圆形障碍物处的转弯半径为：

$ρ = r + d$

其中r为障碍物半径，d为机器人最小安全距离。

3.1.3. 路径中主要参数的计算方法

由上文分析可知，机器人的行走路径为若干个相切的直线和圆弧构成。为方便后续计算，在两圆的公切线上找到一个易于求出坐标的点B (如下图7所示)，这样便将总路径划分为若干个由直线段AC、BD和弧线段CD组成的部分路径。称曲线段ACDB为路径的一个区段。在计算总路径长度等参数时分段计算。

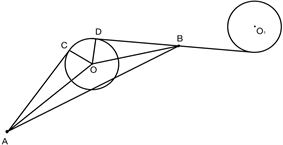
Figure 7. Schematic diagram of a zone

图7. 一个区段示意图

其中，A、B分别为区段的起始点，C、D分别为切点，圆弧半径为r，圆O₁为与BD相切的圆。

B点是一个区段中非常重要但未知的点，首先设两圆圆心坐标为 $O (x_{0}, y_{0}), O_{1} (x_{3}, y_{3})$ ，下面介绍B点在不同情况下的求解方法：

1) B点在两圆同侧公切线上：

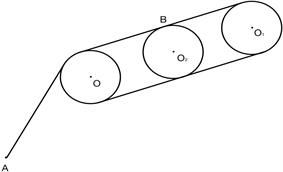
Figure 8. The tangent line lies on the same side of the two circles

图8. 公切线位于两圆同侧

如上图8所示，此时将B点选为公切线的中点。连接OO₁，以OO₁中点 $O_{2} (a, b)$ 为圆点，r为半径做圆，与公切线相交于点 $B (x, y)$ ，连接BO₂。根据中点坐标公式，可得

$a = \frac{x_{0} + x_{3}}{2}$

$b = \frac{y_{0} + y_{3}}{2}$

则圆O₂的方程为

${(x - \frac{x_{0} + x_{3}}{2})}^{2} + {(y - \frac{y_{0} + y_{3}}{2})}^{2} = r^{2}$

由于BO₂垂直于O₁O₂，则BO₂的直线方程为

$y - \frac{y_{0} + y_{3}}{2} = (- \frac{x_{0} - x_{3}}{y_{0} - y_{3}}) (x - \frac{x_{0} + x_{3}}{2})$

联立BO₂的直线方程与圆O₂的方程，即可求解出B点坐标。

2) 点B在两圆异侧公切线上：

当两圆半径相等时：

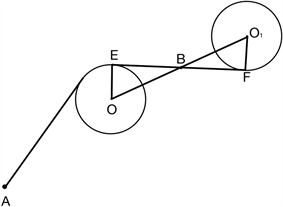
Figure 9. The tangent line lies on the opposite side of two circles of the same radius

图9. 公切线位于相同半径两圆异侧

如上图9所示，此时将B点选为公切线与圆心连线的交点。连接OO₁交公切线于点 $B (x, y)$ ，E、F分别为圆O、O₁的切点。可以明显看出，在∆BOE和∆BO₁F中，有两个角和一条边对应相等，因此 $Δ BOE ≅ Δ {BO}_{1} F$ 。则OB = O₁B，即B为OO₁的中点。由中点坐标公式我们可得

$\begin{array}{l} x = \frac{x_{0} + x_{3}}{2} \\ y = \frac{y_{0} + y_{3}}{2} \end{array}$

当两圆半径不相等时：

如图10所示，此时也将B点选为公切线与圆心连线的交点。连接OO₁交公切线于点 $B (x, y)$ ，E、F分别为圆O、O₁的切点。可以明显看到，在∆BOE和∆BO₁F中，有三个角对应相等，则 $Δ BOE \sim Δ {BO}_{1} F$ ，相似比等于小圆与大圆的半径比，即 $\frac{O B}{O B 1} = \frac{O E}{O 1 F}$ 。根据两点间距离公式及相似比，我们可以得到

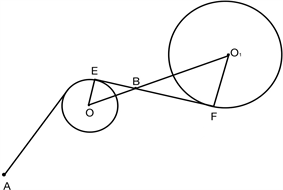
Figure 10. The tangents lie on the opposite sides of two circles with different radius

图10. 公切线位于不同半径两圆异侧

$\frac{\sqrt{{(x - x_{1})}^{2} + {(y - y_{1})}^{2}}}{\sqrt{{(x - x_{3})}^{2} + {(y - y_{3})}^{2}}} = \frac{O E}{O_{1} F}$

同时，点B在OO₁上，则满足

$\frac{x - x_{1}}{y - y_{1}} = \frac{x - x_{3}}{y - y_{3}}$

联立以上两式，即可求解出B点坐标。

下面介绍AC、BD、 $\overset{⌢}{C D}$ 长度的求解方法：

如图所示，设 $A (x_{1}, y_{1}), B (x_{2}, y_{2}), C (m_{1}, n_{1}), D (m_{2}, n_{2}), O (x_{0}, y_{0}), O_{1} (x_{3}, y_{3}),$ 根据两点间距离公式可得

$\begin{array}{l} A O = \sqrt{{(x_{1} - x_{0})}^{2} + {(y_{1} - y_{0})}^{2}} \\ A B = \sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}} \\ O B = \sqrt{{(x_{0} - x_{2})}^{2} + {(y_{0} - y_{2})}^{2}} \end{array}$

在∆OAB中，由OA、OB、AB的长度，利用余弦定理可得

$∠ A O B = \arccos \frac{A O^{2} + B O^{2} - A B^{2}}{2 \times A O \times B O}$ ，

在Rt∆OAC和Rt∆OBD中，我们可以得到

$\begin{array}{l} ∠ A O C = \arccos \frac{r}{A O} \\ ∠ B O D = \arccos \frac{r}{B O} \end{array}$

则有

$∠ C O D = 2 π - ∠ A O B - ∠ A O C - ∠ B O D$ .

最后，可以得到AC、BD、 $\overset{⌢}{C D}$ 的长度为

$\begin{array}{l} \overset{⌢}{C D} = \frac{∠ C O D \times π \times r}{180} \\ A C = \sqrt{A O^{2} - r^{2}} \\ B D = \sqrt{B O^{2} - r^{2}} \end{array}$

因此，机器人在这一区段行走的路程为

$S = A C + \overset{⌢}{C D} + B D$ .

下面介绍两个切点C、D坐标的求解方法：

Figure 11. Calculation of tangent point coordinates

图11. 切点坐标的计算

如上图11所示，由上所述，已知AO、OC的长度，则在Rt∆AOC中由勾股定理可得

$A C = \sqrt{A O^{2} - O C^{2}}$ ，

以AC为半径，A为圆心作圆A，则圆A与圆O相交于C点。易得圆A、圆O的方程分别为

$\begin{array}{l} {(x - x_{1})}^{2} + {(y - y_{1})}^{2} = A C^{2} \\ {(x - x_{0})}^{2} + {(y - y_{0})}^{2} = O C^{2} \end{array}$ .

联立两圆的方程，即可得切点C的坐标。同理，以B为圆心BD为半径作圆B可求解得到另一切点D的坐标。

3.2. 最短时间模型

从O到A的最短路径不一定就是机器人行走时间最短的路径，因此需要重新考虑机器人在障碍物处的转弯圆心以及半径。同样可以利用规划模型来求解，以行走时间最短为目标，找出最合适的转弯圆心和半径，然后利用问题1的模型来求解。

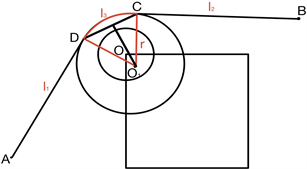
Figure 12. Robot shortest turn process diagram

图12. 机器人最短时间转弯过程图

如图12，设 $A (x_{1}, y_{1}), B (x_{2}, y_{2}), O_{1} (m, n), O (x_{0}, y_{0}), C (m_{1}, n_{1}), D (m_{2}, n_{2})$ ，圆O₁的半径为r，C、D为圆O₁的两个切点，角 $θ = \frac{∠ D O 1 C}{2}$ 。

根据题目要求，机器人距离障碍物最短距离为10个单位，因此

$r - O O_{1} \geq 10,$

即

$r - \sqrt{{(x_{0} - m)}^{2} + {(y_{0} - n)}^{2}} \geq 10$ .

在∆ADO₁和∆BCO₁中，由勾股定理可得

$\begin{array}{l} A O_{1} = \sqrt{A D^{2} + D O_{1}^{2}} \\ B O_{1} = \sqrt{B C^{2} + C O_{1}^{2}} \end{array}$

即

$\begin{array}{l} \sqrt{m_{2}^{2} + n_{2}^{2} + r^{2}} = \sqrt{m^{2} + n^{2}} \\ \sqrt{{(m_{1} - x_{2})}^{2} + {(n_{1} - y_{2})}^{2} + r^{2}} = \sqrt{{(m - x_{2})}^{2} + {(n - y_{2})}^{2}} \end{array}$

同时，点C、D为圆O₁上的点，则CO₁ = DO₁ = r，即

$r = \sqrt{{(m_{1} - m)}^{2} + {(n_{1} - n)}^{2}}, r = \sqrt{{(m_{2} - m)}^{2} + {(n_{2} - n)}^{2}}$

又 $θ = \frac{∠ D O_{1} C}{2}$ ，则 $\sin θ = \frac{C D}{2 r}$ 。根据弦长公式可得

$\overset{⌢}{C D} = 2 \times r \times \arcsin \frac{C D}{2 r}$ ，

由两点距离公式可算出

$C D = \sqrt{{(m_{1} - m_{2})}^{2} + {(n_{1} - n_{2})}^{2}}$ .

根据前面问题1中的证明，我们可以确定点O₁、C、D的范围。其中，

$\begin{array}{l} 80 < m < 230, 0 < n < 210 \\ m_{1} > 80, n_{2} > 210 \end{array}$

因此，联立以上各式和范围可以建立最小规划模型：

$M i n = \frac{l_{1} + l_{2}}{v_{o}} + \frac{l_{3}}{v_{p}}$ ，

$s .t . {\begin{array}{l} r - \sqrt{{(x_{0} - m)}^{2} + {(y_{0} - n)}^{2}} \geq 10 \\ r = \sqrt{{(m_{1} - m)}^{2} + {(n_{1} - n)}^{2}} \\ r = \sqrt{{(m_{2} - m)}^{2} + {(n_{2} - n)}^{2}} \\ \sqrt{m_{2}^{2} + n_{2}^{2} + r^{2}} = \sqrt{m^{2} + n^{2}} \\ \begin{array}{l} \sqrt{{(m_{1} - x_{2})}^{2} + {(n_{1} - y_{2})}^{2} + r^{2}} = \sqrt{{(m - x_{2})}^{2} + {(n - y_{2})}^{2}} \\ l_{1} = \sqrt{m^{2} + n^{2} - r^{2}} \\ l_{2} = \sqrt{{(m - x_{2})}^{2} + {(n - y_{2})}^{2} - r^{2}} \\ l_{3} = 2 \times r \times \arcsin (\frac{d}{2 r}) \\ d = \sqrt{{(m_{1} - m_{2})}^{2} + {(n_{1} - n_{2})}^{2}} \end{array} \\ 80 < m < 230 \\ n_{1} > 210 \\ m_{1} < 80 \\ 0 < n < 210 \end{array}$

4. 模型求解

4.1. 最短路径模型的求解

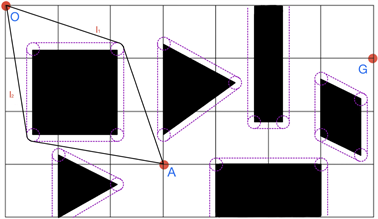
Figure 13. The possible paths of O→A

图13. O→A的可能路径

如上图13所示，根据机器人的行走原则，找到了两条可能较短的路径 $l_{1}, l_{2}$ 。根据上述计算方法利用MATLAB求解 [6] 并比较，可得 $l_{1}$ 的路径最短，为471.0372个单位。

下表1给出了路径中每段直线段或圆弧的起点和终点坐标，圆弧的圆心坐标以及机器人行走的总距离和总时间。

Table 1. Detailed solution of the shortest path O→A

表1. O→A最短路径的详细求解

4.2. 最短时间模型的求解

利用LINGO软件代入数据进行求解，结果显示机器人行走的最短时间为94.22825秒，转弯半径为r = 12.9886。如图14所示。

表2给出了路径中每段直线段或圆弧的起点和终点坐标，圆弧的圆心坐标以及机器人行走的总距离和总时间。

5. 总结与展望

5.1. 研究结论

通过运用栅格建模以及线性规划模型、最短路径模型给出了机器人行走的原则，为机器人可能路径的选择提供了依据，同时讨论了行走路径中机器人直线段长度和弧线段长度的计算方法，以及直线与圆弧切点坐标的计算方法，为后续问题的解决提供了很好的工具；最短时间模型中，以行走时间最短为目标，找出了最合适的转弯圆心和半径，然后利用问题1的模型求得了最优解。

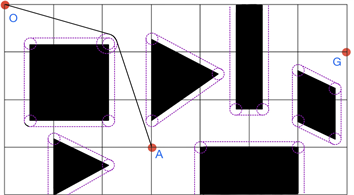
Figure 14. The minimum time travel chart of O→A

图14. O→A的最短时间路程图

Table 2. Detailed solution for the minimum time path O→A

表2. O→A最短时间路径的详细求解

根据计算，本文得到从O走到A的最短路径为471.0372个单位，此时需要走的时间为96.0176秒；从O走到A的最短时间为94.2283秒，此时需要走的路程长度为481.129个单位。这说明从O到A的最短路径不一定就是机器人行走时间最短的路径，采用最短时间的方式可以提高工作效率，但是转弯的弧度更大，对机器人自身的损耗也较大；反之采取最短路径的方式，走的直线段较多，转弯的弧度小，但效率相对不那么高。因此实际应用中，我们可以根据机器人的工作性质以及工作场景障碍物的分布情况，来决定机器人的行走路径。

相对实际情况来说，模型只考虑了机器人匀速行走的情况，并没有考虑机器人从静止到行走以及在行走过程中加速和减速的过程，这使模型的应用有比较大的局限性。同时，利用该模型在计算过程中存在较大的计算误差，影响结果的精确性。可以考虑把机器人变速的问题考虑进去，建立一个复杂的适用范围广的模型，以解决更复杂的问题，同时尽量控制误差，保证结果精确性。

5.2. 模型应用

我们知道，实际情况中，机器人在工作时遇到的障碍物更多，可行路径也更加复杂。为检验上节所述模型的可行性，我们利用上述最短路径模型来求O点到G点的最短路径。

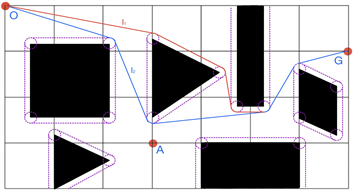
Figure 15. The possible paths of O→G

图15. O→G的可能路径

如上图15所示，根据机器人的行走原则，我们找到了两条可能较短的路径 $l_{1}, l_{2}$ 。根据上述计算方法利用MATLAB求解并比较，可得 $l_{1}$ 的路径最短，为853.7002个单位。

下表3给出了路径中每段直线段或圆弧的起点和终点坐标，圆弧的圆心坐标以及机器人行走的总距离和总时间。

Table 3. Detailed solution of the shortest path O→G

表3. O→G最短路径的详细求解

实际应用中，本模型适用于对结果精度要求不高和速度恒定的机器人最优路径选择的场景中。比如物流仓库物流机器人行驶路径的选择、科创比赛中机器人路径的选择等场景。

致谢

作者感谢河南工业大学理学院教研项目(lxyjy202106, lxyjy202215)，河南省教育厅项目(YJS2022JC16)以及河南省外专项目(HNGD2022044)资助。

文章引用

王梦甜,张巍,陈晓友. 基于线性规划下的机器人最优避障路径模型
Optimal Obstacle Avoidance Path Model for Robots Based on Linear Programming[J]. 建模与仿真, 2022, 11(04): 1083-1095. https://doi.org/10.12677/MOS.2022.114099

参考文献

1. 朱宝艳. 移动机器人全覆盖遍历路径规划算法研究[D]: [硕士学位论文]. 淄博: 山东理工大学, 2017.

2. 陈鹏. 移动机器人全遍历覆盖路径规划研究[D]: [硕士学位论文]. 淄博: 山东理工大学, 2014.

3. 陈逸怀, 朱博. 基于单元分解法的移动机器人遍历路径规划[J]. 装备制造技术, 2014(4): 148-149+152.

4. 李文彪. 基于深度强化学习的工业机器人避障路径规划方法[J]. 制造业自动化, 2022, 44(1): 127-130.

5. Habib, Md.A., Alam, M.S. and Siddique, N.H. (2012) Optimizing Coverage Performance of Multiple Random Path-Planning Robots. Paladyn, Journal of Behavioral Robotics, 3, 11-22. https://doi.org/10.2478/s13230-012-0012-5

6. 司守奎. 数学建模算法与应用[M]. 北京: 国防工业出版社, 2011.

NOTES

^*通讯作者。

期刊菜单