Statistics and Application
Vol.
09
No.
06
(
2020
), Article ID:
39628
,
12
pages
10.12677/SA.2020.96110
前馈神经网络在多元函数逼近中的应用
葛悠然1,翟九媛2,马尧鹏3,王汉权1*
1云南财经大学,统计与数学学院,云南 昆明
2云南大学,经济学院,云南 昆明
3云南财经大学,云南 昆明
收稿日期:2020年11月29日;录用日期:2020年12月22日;发布日期:2020年12月31日

摘要
给定一组数据(例如一些点及相应点处的函数值),找到未知函数的表达公式——函数逼近问题是数学与工程应用中的一个基本问题。传统的数值方法多采用多项式插值法(例如拉格朗日插值法、牛顿插值法、三次样条法等),本文通过构造前馈神经网络函数得到未知函数的表达式,讨论其处理函数逼近问题的优缺点。具体说来,先介绍训练多元函数的前馈神经网络的详细计算过程,然后分析隐含层节点数目对该网络的精度影响问题。最后通过数值计算结果证实前馈神经网络可用来逼近一元函数、二元函数、三元函数,能够达到较高的计算精度。本文的讨论适用于其他类人工神经网络在四元或四元以上的多元函数逼近问题的研究,也有助于理解相关人工神经网络的基本性质与作用。
关键词
前馈神经网络,函数逼近,隐含层节点数目
Application of Feedforward Neura Networks in Multivariate Function Approximation
Youran Ge1, Jiuyuan Zhai2, Yaopeng Ma3, Hanquan Wang1*
1School of Statistics and Mathematics, Yunnan University of Finance and Economics, Yunnan Kunming
2School of Economics, Yunnan University, Yunnan Kunming
3Yunnan University of Finance and Economics, Yunnan Kunming
Received: Nov. 29th, 2020; accepted: Dec. 22nd, 2020; published: Dec. 31st, 2020

ABSTRACT
Given a set of data (such as some points and function values at corresponding points), finding the expression formula of the unknown function—the function approximation problem is a fundamental problem in mathematics and engineering applications. Traditional numerical methods mostly use polynomial interpolation (such as Lagrangian interpolation, Newton interpolation, cubic spline method, etc.). In this paper, the expression of the unknown function is obtained by constructing the feedforward neural network function, and the advantages and disadvantages of the approximation problem of the processing function are discussed. Specifically, the detailed calculation process of the feedforward neural network for training multivariate functions is first introduced, and then the influence of the number of hidden layer nodes on the accuracy of the network is analyzed. Finally, the numerical results show that the feedforward neural network can be used to approximate the unary function, the binary function and the ternary function, which can achieve higher calculation accuracy. The discussion in this paper is applicable to the study of multivariate function approximation problems of other artificial neural networks in quaternary or quadruple, and it also helps to understand the basic properties and effects of related artificial neural networks.
Keywords:Feedforward Neural Network, Function Approximation, Number of Hidden Layer Nodes

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
给定一组数据,找到能代表该数组的函数表达式是数学与工程应用中的一个基本问题。函数逼近问题能够应用于解决地震勘探、信号处理、物理探矿等方面的实际问题 [1]。随着计算机技术的不断发展,人工神经网络已经成为简便的计算工具。人工神经网络处理数据具有计算简便、耗时短、精度高等优点 [2],很多大数据复杂计算问题应用人工神经网络来解决。前馈神经网络作为人工神经网络的一个重要分支,研究它在多元函数逼近中的应用,一方面可解决前述基本问题,另一方面,通过研究该基本问题可验证它的性能、掌握训练神经网络的主要步骤。
由于人工神经网络解决函数逼近问题时便捷、精准的特点,在上世纪,人们就开始了对它的研究。早在20世纪90年代,国外的学者们就已经开始了对人工神经网络解决函数逼近问题的早期探索。在1993年,Bulsari A. [3] 提出了利用前馈神经网络解决一些特殊函数的逼近问题,并选用Sigmoid函数作为网络的传递函数来构造函数逼近网络。在1998年,Suzuki和Shin [4] 证明了三层人工神经网络可以应用于三角函数、分段线性函数的逼近问题。同年,Twomey J. M.和Smith A. E. [5] 应用人工神经网络可以解决数据不足时的函数逼近问题。随后,在2005年,Ferrari S.和Stengel R. F. [6] 利用前馈神经网络解决非线性函数逼近问题。在2013年,S. Yao、C. J. Wei和Z. Y. He [7] 将前馈神经网络中的RBF网络、BP网络和GRNN网络的性能进行比较,分析得出RBF网络在函数逼近中的精度和速度方面最优。
国内学者在20世纪末开始对人工神经网络解决函数逼近的问题进行研究。在1997年,韦岗、李华和徐秉铮 [8] 首次证明了前馈神经网络的隐含层神经元数目足够多时,其多维函数逼近能力与维数无关。该定理大大简化了前馈多层神经网络函数逼近问题的分析难度。在2005年,王强、余岳峰和张浩炯 [9] 以一个一维非线性函数为例论述了一个单隐层的前馈神经网络解决函数逼近问题的过程。随后,在2009年,侯木舟 [10] 提出了前馈多层神经网络函数逼近问题在股市数据预测、环境数据预测、EGG信号预测等方面的应用问题。在2016年,李鹏柱 [11] 研究了前馈神经网络的函数逼近中优化激活函数和固定权值的问题。
本文的研究建立在前人的研究基础上,主要有下述贡献点:寻找前馈神经网络中最适隐含层节点数目来增加网络的逼近精度;提出一种新的训练方法——贝叶斯归一化法 [12],将参数映射到小范围内,使得求解极小值问题的收敛速度更快捷;最后总结了所构造的网络在所有函数逼近问题中的普遍应用的可能性。
2. 理论准备
2.1. 前馈神经网络
人工神经网络可分为前馈型和反馈型,相对于反馈型神经网络,前馈型神经网络各网络层的神经元间互不连接 [13],即此网络各层之间没有反馈,是一种最简单的神经网络。
前馈神经网络中一般包括多层网络,每层网络有多个神经元。信息输入到输入层,单向传递到隐含层加入权值和阈值,经传递函数运算后到输出层,最后由输出层输出结果 [14]。
如图1所示,记 为第1层隐含层的权值矩阵, 为第2层隐含层的权值矩阵, 为第l层隐含层的权值矩阵, 为输出层的权值矩阵;记 为第1层隐含层的阈值矩阵, 为第2层隐含层的阈值矩阵, 为第l层隐含层的阈值矩阵, 为输出层的阈值矩阵; 为第1层隐含层的传递函数, 为第2层隐含层的传递函数, 为第l层隐含层的传递函数,且所有传递函数默认为光滑连续的函数; 为输出层函数 [6] [15]。

Figure 1. Feed forward neural network diagram
图1. 前馈神经网络简图
令x为输入数据矩阵,计算该数据传递到第1层隐含层得到输出值为
(1)
然后经过第2层隐含层得到输出值为
(2)
依次向下传递到第l层隐含层得到输出值为
(3)
最后传递到输出层输出网络的结果为
(4)
前馈神经网络的工作过程分为正向传递学习和反向传递训练两个过程 [16],其工作原理主要是对所涉及到的参数进行调整,最终使得网络误差最小。其中正向传递学习过程中,数据通过输入层进入网络,在隐含层中,代入权值和阈值、传递函数运算后,传到输出层。比较输出值和期望值,如若差别很大,则进行反向传递训练过程。在反向传递训练过程中,采用特定的训练方式,不断更新网络的权值和阈值,直到网络的输出与期望输出之间误差最小,最终得到一个精准的前馈神经网络。
2.2. 函数逼近问题
在数学研究和工程应用中存在以下函数逼近问题:已知函数 ,找到某类选定函数中的特定函数 ,使得 可以在一定意义下近似表示 ,并求出近似误差。在函数逼近问题中,逼近已知函数的函数类是多样化的;即使确定了函数类范围,其中特定逼近函数 仍然是多种多样的;另外特定逼近函数 与被逼进函数 的逼近误差的定义方式也不同。逼近函数有许多方法,包括插值法、线性(或非线性)回归法、基函数展开法、数理统计方法 [16]。
本文通过构造前馈神经网络函数来讨论函数逼近问题。它可以简单理解为用输入数据多次训练网络逼近函数,从而得到一个精准的神经网络函数,以便后续调用和改进。
2.3. 构造函数的逼近网格
构造逼近函数的前馈神经网络大致分为以下四个步骤:
第一步,给定的一组数据。本文中选取函数定义域中的N个点及点处的函数值作为已知数据: 。
第二步,选择前馈神经网络的结构,包括网络层数目,各层神经元的数目,以及传递函数,进而构造出前馈神经网络函数(参见公式(4))。
第三步,训练前馈神经网络的参数。
若前馈神经网络的误差函数 [17] 定义为
(5)
其中, 为神经网络输出函数,其形式如公式(4)所示。 为给定的N个样本,w为权值矩阵,b为阈值矩阵。
该训练过程的目标是求出特殊的权值矩阵 和阈值矩阵 ,使得此时的目标误差函数 最小(接近于0),输出此时的权值矩阵 和阈值矩阵 ,代入激活函数中求得该神经网络函数。训练过程就是利用迭代法求解如下极小值问题:
找特殊的权值矩阵 和阈值矩阵 使得 对任意的权值矩阵w和阈值矩阵b都成立。
第四步,得出该网络函数表达式 ,并画出所训练的前馈神经网络和原函数的对比图,同时结合网络的输出值的绝对值误差图来分析网络的精度。
注意:
(1) 在第二步中,隐含层节点数目多少与网络的逼近精度有关。对于隐含层节点数目,过少会导致网络不拟合函数,而节点数目太多会造成网络的过适性现象,所以可以通过改变其隐含层节点数目来优化网络的效果。本文中各隐含层的传递函数选择“ ”函数 [5],此函数光滑连续符合网络的传递函数要求,其函数表达式如下:
(6)
在隐含层和输出层之间的传递函数选择“ ”函数 [5],此函数值可以取任意值,符合网络的输出范围要求。其函数表达式如下:
(7)
(2) 在第三步中,选择何种求极小值问题的迭代方法也很重要,这会影响整个网络的逼近精度。本文选择MATLAB中的“ ”函数 [5] 来训练该网络。该函数利用一种随机梯度下降法——贝叶斯归一化法来求解上述极小值问题。在贝叶斯归一化法使用过程中 [17],假定网络的权值和阈值是按照指定分布随机可变的,根据贝叶斯法则更新权值和阈值密度函数,再求均方误差函数最小时的权值和阈值。“ ”函数将参数映射到小范围内,使得求解极小值问题的收敛速度更快捷。
3. 构造逼近多元函数的前馈神经网络
3.1. 一元函数
对于一元函数的逼近网络,我们选择“1-n-1”类型的前馈神经网络,即该网络含有一个输入层、一个输出层和一个隐含层,其中输入层和输出层各有一个神经元,隐含层有n个神经元。通过试验发现不同函数的最适隐含层神经元数目不同,所以要具体函数具体分析。
以函数 为例,定义 ,选取 时、间距为0.1的 数据组作为输入数据,构建的前馈神经网络参数设定为训练迭代次数为105次,训练目标误差函数值小于1 × 10−10,当隐含层节点数目为27~31个时,网络对该一元函数逼近的绝对值误差( )如表1所示:
Table 1. Absolute value error ( | F ( x → ) − y w , b ( x → ) | ) of F ( x ) = { | x | ∗ cos ( x ) , x < 0 e x − 1 , x ≥ 0 neurons in different hidden layers
表1. 函数不同隐含层神经元的绝对值误差( )
表1结合不同隐含层节点数目的网络逼近函数图观察得,节点数目在27~29时,网络的误差逐渐变小,节点数目在30及以上时,网络的误差变大。综上可得,隐含层节点数目为29个时,对应前馈神经网络对函数 逼近效果最好。
加入以上最适隐含层神经元数目后,创建训练该网络,然后输出训练后网络的权值矩阵和阈值矩阵如下:
,
由上面计算得到的数值,可得如下神经网络函数:
(8)
从图2中(右)图可以看出逼近该一元函数的前馈神经网络的误差绝对值在 之间,结合其中网络输出结果与输入样本对比图分析可知,该网络逼近效果较好。
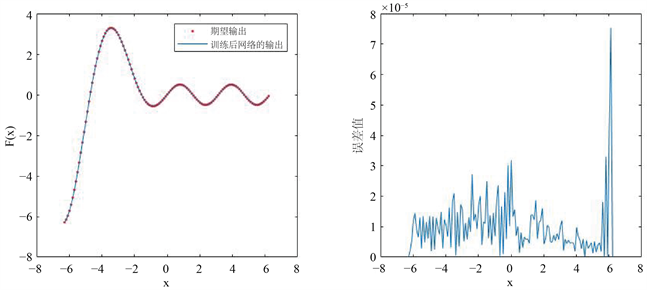
Figure 2. (left) A comparison between the output of the network and the input sample, and (right) an absolute value error ( ) graph approximated by the network
图2. (左) 该网络输出结果与输入样本的对比图,(右) 该网络逼近的绝对值误差( )图
3.2. 二元函数
对于二元函数的逼近网络,我们选择“1-n-m-1”类型的前馈神经网络,即该网络含有一个输入层、一个输出层和两个隐含层,其中输入层和输出层各有一个神经元,两个隐含层分别有n个和m个神经元。
以函数 为例,定义 ,选取 时、间距为0.1的 数据组作为输入数据,构建的前馈神经网络参数设定为训练迭代次数为105次,训练目标误差函数值小于1 × 10−10,当隐含层节点数目分别为15~19个时,网络对1 × 10−10该函数逼近误差如表2所示:
Table 2. Absolute value error ( | F ( x → ) − y w , b ( x → ) | ) of neurons in different hidden layers of this binary function
表2. 该二元函数不同隐含层神经元的绝对值误差( )
分析表2数据,结合不同隐含层节点数目的网络逼近函数图观察得,第1层隐含层神经元数目为17且第2层隐含层神经元数目为16时,该网络的精度最高。
加入以上最适隐含层神经元数目后,创建训练该网络,然后输出训练后网络的权值矩阵和阈值如下:
,,

由上面计算得到的数值,可得如下神经网络函数:
(9)
从图3中(右)图可以看出逼近该二元函数的前馈神经网络的误差绝对值在 之间,结合其中网络原函数图像与网络输出结果图对比分析可知,该网络逼近效果较好。
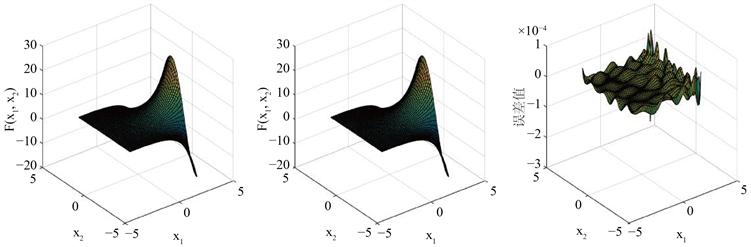
Figure 3. (left) original function image, (middle) output result diagram, (right) absolute value error ( ) diagram of the network approximation
图3. (左) 原函数图像,(中) 该网络输出结果图,(右) 该网络逼近的绝对值误差( )图
3.3. 三元函数
对于三元函数的逼近网络,我们选择“1-n-m-k-1”类型的前馈神经网络,即该网络含有一个输入层、一个输出层和三个隐含层,其中输入层和输出层各有一个神经元,三个隐含层分别有n个、m个和k个神经元。
以函数 为例,定义 ,选取 时、间距为0.3的 数据组作为输入数据,构建的前馈神经网络参数设定为训练迭代次数为105次,训练目标的误差小于1 × 10−10,当隐含层节点数目分别为8~12个时,网络对该函数逼近误差如表3~表5所示:
Table 3. When the number of neurons in the first layer is 8, the absolute value error ( | F ( x → ) − y w , b ( x → ) | ) of the network approximation to the ternary function
表3. 第1层隐含层神经元数目为8个时,网络对该三元函数逼近的绝对值误差( )
Table 4. When the number of neurons in the first layer is 9, the absolute value error ( | F ( x → ) − y w , b ( x → ) | ) of the network approximation to the ternary function
表4. 第1层隐含层神经元数目为9个时,网络对该三元函数逼近的绝对值误差( )
Table 5. When the number of neurons in the first layer is 10, the absolute value error ( | F ( x → ) − y w , b ( x → ) | ) of the network approximation to the ternary function
表5. 第1层隐含层神经元数目为10个时,网络对该三元函数逼近的绝对值误差( )
分析以表3、表4和表5的数据,结合不同隐含层节点数目的网络逼近函数图观察得,三层隐含层神经元数目均为10时,网络的精度最高。
加入以上最适隐含层神经元数目后,创建训练该网络,然后输出训练后网络的权值矩阵和阈值矩阵如下:
,,,
由上面计算得到的数值,可得如下神经网络函数:
(10)
从图4中(右)图可以看出逼近该三元函数的前馈神经网络的误差绝对值在 之间,结合其中原函数图像和网络输出结果对比分析可知,该网络逼近效果较好。
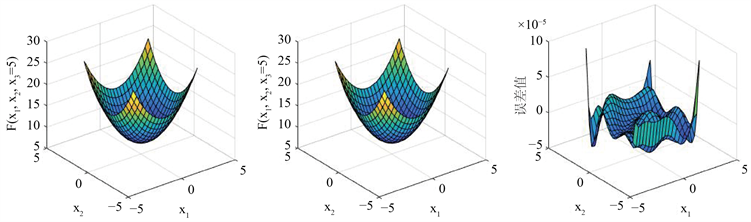
Figure 4. (left) original function image, (middle) output result diagram of the network, (right) absolute value error ( ) diagram of the network approximation
图4. (左) 原函数图像,(中) 该网络输出结果图,(右) 该网络逼近的绝对值误差( )图
4. 结语
本文通过数值计算结果证实前馈神经网络可用来逼近一元函数、二元函数、三元函数,能够达到较高的计算精度。发现输入样本的数量多少会影响神经网络计算的速度和精度,神经网络隐含层数目也会影响神经网络的逼近精度,建议同时改变输入样本的数量和隐含层数目来增加神经网络的逼近精度。本文的讨论具有一般性,适用于其他类人工神经网络在四元或四元以上的多元函数逼近问题的研究,也有助于理解相关人工神经网络的基本性质与作用。
文章引用
葛悠然,翟九媛,马尧鹏,王汉权. 前馈神经网络在多元函数逼近中的应用
Application of Feedforward Neura Networks in Multivariate Function Approximation[J]. 统计学与应用, 2020, 09(06): 1048-1059. https://doi.org/10.12677/SA.2020.96110
参考文献
- 1. 沈燮昌. 逼近论发展史简述(一) [J]. 数学研究及应用, 1982, 2(2): 171-180.
- 2. 徐学良. 人工神经网络的发展及现状[J]. 微电子学, 2017, 47(2): 239-242.
- 3. Bulsari, A. (1993) Some Analytical Solutions to the General Approximation Problem for Feedforward Neural Networks. Neural Networks, 6, 991-996.
https://doi.org/10.1016/S0893-6080(09)80008-7 - 4. Suzuki, S. (1998) Constructive Function-Approximation by Three-Layer Artificial Neural Networks. Neural Networks, 11, 1049-1058.
https://doi.org/10.1016/S0893-6080(98)00068-9 - 5. Twomey, J.M. and Smith, A.E. (1998) Bias and Variance of Validation Methods for Function Approximation Neural Networks under Conditions of Sparse Data. IEEE Transactions on Systems, Man and Cybernetics, Part C (Applications and Reviews), 28, 417-430.
https://doi.org/10.1109/5326.704579 - 6. Ferrari, S. and Stengel, R.F. (2005) Smooth Function Approximation Using Neural Networks. IEEE Transactions on Neural Networks, 16, 24-38.
https://doi.org/10.1109/TNN.2004.836233 - 7. Yao, S., Wei, C.J. and He, Z.Y. (2013) Evolving Wavelet Neural Networks for Function Approximation. Electronics Letters, 17, 586-594.
- 8. 韦岗, 李华, 徐秉铮. 关于前馈多层神经网络多维函数逼近能力的一个定理[J]. 电子与信息学报, 1997, 19(4): 433-438.
- 9. 王强, 余岳峰, 张浩炯. 利用人工神经网络实现函数逼近[J]. 计算机仿真, 2002(5): 44-47.
- 10. 侯木舟. 基于构造型前馈神经网络的函数逼近与应用[D]: [博士学位论文]. 长沙: 中南大学, 2009.
- 11. 李鹏柱. 关于神经网络与样条函数的逼近性能研究[D]: [硕士学位论文]. 银川: 宁夏大学, 2016.
- 12. 许洋. 前馈型神经网络算法优化分析[J]. 硅谷, 2014(13): 66, 42.
- 13. Heaton, J.B., Polson, N.G. and Witte, J.H. (2018) Deep Learning in Finance.
- 14. 周开利. 神经网络模型及其MATLAB仿真程序设计[M]. 北京: 清华大学出版社, 2005.
- 15. 孙永生. 函数逼近论[M]. 北京: 北京师范大学出版社, 1989.
- 16. 李晓东, 胡志恒, 虞厥邦. 一种前馈神经网络的快速学习算法[J]. 信号处理, 2004, 20(2): 184-187.
- 17. Foresee, F.D. and Hagan, M.T. (1997) Gauss-Newton Approximation to Bayesian Regularization. International-Joint Conference on Neural Network, 1930-1935.
NOTES
*通讯作者。
