Advances in Applied Mathematics
Vol.
10
No.
03
(
2021
), Article ID:
41243
,
11
pages
10.12677/AAM.2021.103084
跳扩散模型下稳健最优再保险和CDS投资策略
于亚丽,李晓芳,高豪
河北工业大学,天津

收稿日期:2021年2月23日;录用日期:2021年3月19日;发布日期:2021年3月26日

摘要
本文研究了跳扩散风险模型下,具有模糊厌恶的保险公司的最优投资与再保险策略问题。假设保险公司可以购买比例再保险,也可以投资于一个无风险资产、一个风险资产和一种信用违约互换债券构成的金融市场。我们在均值–方差准则下,最大化终端财富的期望。根据扩展的Hamilton-Jacobi-Bellman (HJB)方程,我们求出了违约前和违约后的最优投资与再保险策略。最后,我们给出了一些数值例子验证模型不确定性和信用违约互换债券投资对策略的影响。
关键词
跳扩散,模糊厌恶,均值–方差,信用违约互换
Robust Optimal Proportional Reinsurance and CDS Investment Strategies for Insurer with Jump-Diffusion Risk
Yali Yu, Xiaofang Li, Hao Gao
Hebei University of Technology, Tianjin

Received: Feb. 23rd, 2021; accepted: Mar. 19th, 2021; published: Mar. 26th, 2021

ABSTRACT
This paper considers an optimal reinsurance and investment problem in a model with jump diffusion for an ambiguity averse insurer (AAI). The insurer is allowed to purchase proportional reinsurance and invest in a financial market, which consists of a risk-free asset, a risky asset and a credit default swap (CDS). We maximize the expectation of the terminal wealth under the mean-variance criterion. By solving the corresponding extended Hamilton-Jacobi-Bellman (HJB) equations, the optimal investment-reinsurance strategies and the corresponding equilibrium value functions are obtained for the post-default case and pre-default case. Finally, we provide numerical examples to illustrate the effects of model uncertainty and Credit Default Swap (CDS).
Keywords:Jump-Diffusion, Ambiguity Averse, Mean-Variance, Credit Default Swap

Copyright © 2021 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
投资和再保险是保险公司增加财富和降低风险的重要方式。近几年来,很多学者采用不同的目标函数研究投资问题。Yang和Zhang [1] 最大化终端财富的指数效用函数的期望,并求出了闭式表达式。然而,保险公司仅仅投资于一个风险资产,其价格过程由带跳的风险模型描述。Cao和Peng [2] 在均值–方差准则下扩展了上述投资问题。他们假设保险公司投资于一个无风险资产和n个风险资产,通过最优性原理求出了最优投资策略。此外,Promislow和Young [3] 研究了破产概率最小化问题,求出了显示表达式。
但是,上述文献研究中,均没有考虑违约债券。事实上,自2014年以来,违约数量与资金规模高涨。因此,保险公司在投资过程中考虑违约债券很重要。Wang和Zhang [4] 假设投资于一个无风险资产、一个风险资产和一种可违约债券,并求解出稳健最优投资和再保险策略。Zhao [5] 等人用博弈论方法,研究了具有损失厌恶的保险公司将资产投资于一种具体的CDS违约债券和超额损失再保险,推导出了最有策略和值函数的显示解。
在目前的研究中,除了 [5],很少有人同时考虑鲁棒最优再保险和CDS投资问题。然而,他们只把资产投资在无风险资产和CDS中,忽略了投资在风险资产的必要性。在本篇文章中,受Zhao [5] 和Zeng [6] 的启发,我们把盈余投资到无风险资产、风险资产和CDS中增加收益,其风险资产的价格过程符合跳扩散风险模型。此外,保险公司还购买了比例再保险分散风险,这样做更符合现实的金融市场。通过扩展相应的HJB方程,得出违约前和违约后的稳健最优投资再保险策略和违约后的均衡值函数。
本文的安排内容如下:第2节给出了模型的基本假设。第3节提出了模型不确定性下的均值–方差动态问题。第4节推导了违约前和违约后的稳健最优再保险和投资策略,并求出相应的均衡值函数。第5节提供了数值分析。
2. 模型假设
设
是完备的概率空间,
右连续,
和
是两个独立的标准布朗运动,
和
是两个泊松过程,
和
是两个随机变量。
2.1. 盈余过程
假设保险公司的盈余过程服从经典的Cram’er-Lundberg风险模型:
其中c是保费率,
是复合泊松过程,表示在
区间上的累计索赔。
是强度为
的齐次泊松过程。
是正的独立同分布的随机变量,其分布函数为F(y)。令
的一阶矩为
,二阶矩为
。我们用期望值法计算保费,即
,其中
是保险公司的安全荷载。
假设保险公司可以购买比例再保险对冲风险。令
为再保险比例水平,根据期望值原则,再保费为
,其中
是再保险公司的安全荷载。考虑再保险后的盈余过程为:
(1)
2.2. 金融市场
在金融市场中,保险公司为了增加财富,将资产投资于一种无风险资产、一种风险资产和CDS债券。假设风险资产的价格B(t)满足:
(2)
其中,r > 0是无风险资产利率。假设风险资产St的价格过程满足跳扩散风险模型
(3)
其中漂移系数μ和扩散系数σ都是正的常数;W(t)是标准布朗运动;
是复合泊松过程,表示在[0, t]区间上风险资产发生跳的累计数量;
是强度为
的齐次泊松过程。
是正的独立同分布的随机变量,其分布函数为G(z)。令
的一阶矩为
,二阶矩为
。
接下来,我们考虑CDS。记H(t)是违约过程。如果保险公司在t时刻发生违约,则H(t) = 1;否则H(t) = 0。定义违约时间:
根据Zhao Hui [5] 提出的结论,违约前和违约后的CDS价格如下:
和
(4)
CDS的市场价格C(t)为:
(5)
其中,
是违约前t时刻的市场价格,T1是CDS的交割期。H(t)是在风险中性测度S下,强度为h的泊松过程。
记保险公司因保护买方收到CDS的累计分红过程D(t)为:
(6)
当违约发生时,
是保险公司给再保险公司的累计支出。根据鞅的定义可知,
(7)
是一个鞅。记hp是违约过程H在实际测度P下的强度。则CDS在P下的价格满足:
(8)
其中,
是保险公司付给买方支付的差价;
是当违约发生时,卖方支付给保险公司的损失率。
记
是保险公司的全部财富,
是在t时刻投资在风险资产的财富,
是在t时刻投资在CDS的财富比例,则
是在t时刻投资在无风险资产的财富。假设交易策略是一个三维数组
,保险公司考虑
后的财富过程满足如下方程:
(9)
根据大数据得出结论,相比起盈利来说,投资人更喜欢规避风险。我们发现参考概率P下的参考模型只是近似于真实模型,通过等价概率测度Q近似测度P:
。
接下来定义一个实值的G可料过程
(10)
其中,
。
根据Girsanov’s定理得知,
、 和
三个泊松过程的强度分别为
、 和
。则保险公司在Q下的财富过程为:
(11)
其中,
。
定义2.1 (可行策略)对任意
,若交易策略是可行的需满足以下条件:
1)
,且
是G可料的;
2) 对任意
,,,其中
是最坏情况下的等概率测度。
3)
是随机微分方程(11)的强解。
3. 模型不确定下的均值–方差问题
我们假设最优问题是传统的均值–方差问题,即:
(12)
其中,
,,风险规避系数
。
上述模型(12)忽略了模型不确定,这可能会导致错误定价。接下来,我们考虑最坏情况下的惩罚目标函数:
(13)
其中,
(14)
(13)式中的
和
是在P下非负的风险规避参数。
和
是测量风险模型中具有跳风险的相对熵。则(13)式中的第一项是从参考度量到替代度量的惩罚。保险公司考虑鲁棒性后的均值–方差问题如下:
(15)
由于均值–方差是时间不一致的,为了找到时间一致性下的解,我们定义下面的均衡策略和值函数:
定义3.1 对任意的
, 和一个可行策略
,定义一个可行策略:
如果
,那么
是一个均衡策略;
是一个均衡值函数。
接下来定义无穷小生成元:
(16)
下面给出了违约后和违约前的有关HJB方程的验证定理。
定理3.1 (违约后的证明定理)当Z = 1时,对任意的
,如果存在两个实值函数
和
满足下面的扩展的HJB方程:
(17)
(18)
(19)
(20)
和
(21)
则
是稳健投资再保险策略,
,。
定理3.2 (违约前的证明定理) 当Z = 0时,对任意的
,如果存在两个实值函数
和
满足下面的扩展的HJB方程:
(22)
(23)
(24)
(25)
和
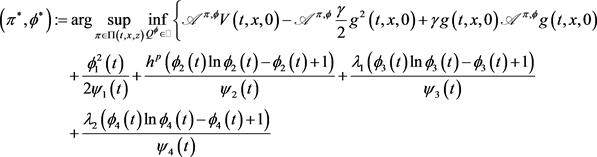 (26)
(26)
则
是稳健投资再保险策略,
,。
4. 求解稳健最优问题
在这一节中,我们求解出了违约前和违约后的稳健最优投资策略和均衡值函数的表达式。我们选取了模糊厌恶的偏好参数,
、、 和
。
4.1. 违约后的情况:z = 1
在这种违约已经发生的情况下,CDS不再是可投资的资产,即投资在CDS上的资产为0。
定理4.1 保险公司违约后的最优投资和再保险策略为:
(27)
(28)
相应的均衡值函数为:
其中,
(29)
(30)
(31)
(32)
终端盈余的期望函数为:
其中,
(33)
(34)
其中,
(35)
(36)
4.2. 违约前的情况:Z = 0
定理4.2 当违约发生前,稳健最优投资再保险策略为:
(37)
(38)
(39)
相应的均衡值函数是:
其中,a(t)和b(t)满足:
(40)
(41)
其中,
(42)
(43)
(44)
终端盈余的期望函数为:
其中,
(45)
(46)
其中,
(47)
(48)
(19)
5. 数值分析
在这一节中,我们用数值例子来验证模型不确定性和CDS投资对最优策略的影响。基础参数如下

参数对最优策略的影响
图1展示了模糊厌恶系数
和风险规避系数
对鲁棒最优再保险策略
的影响。从图1中我们可以看出,当
和
减小时,
反而增加,所以保险公司更愿意购买再保险去降低风险。图2展示了风险模型中跳扩散系数
和再保险公司的安全荷载
对鲁棒最优再保险策略
的影响。从图2中我们可以看出,当
增加,保险公司增加对再保险的投资。当
的强度增大时,保险公司为了减少支出,降低对再保险的投资。
图1.
和
对
的影响
图2.
和
对
的影响
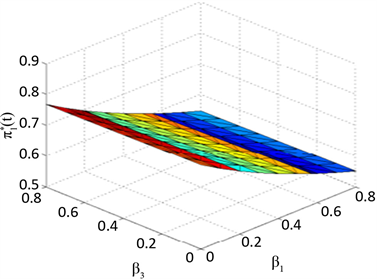
Figure 3. Effects of
and
on
图3.
和
对
的影响

Figure 4. Effects of
and
on
图4.
和
对
的影响
图3展示了模糊厌恶系数
和模糊厌恶系数
对鲁棒最优投资
的影响。从图3中我们可以看出,随着
和
的增加,保险公司降低对风险资产的投资。
图4展示了违约强度
和
对CDS投资
的影响。当
增强时,保险公司明显减少对
的投资。当
增加时,保险公司增加对
的影响。
6. 总结
在这篇文章中,我们研究了保险公司在模糊厌恶和考虑CDS投资的情况下,求解稳健最优投资和再保险问题。为了最大可能地增加财富,保险公司把盈余投资到无风险资产、风险资产和CDS。通过扩展的HJB方程,我们求解了最优投资和再保险的均衡策略。在文章最后,我们给出了数值进行敏感性分析。
文章引用
于亚丽,李晓芳,高 豪. 跳扩散模型下稳健最优再保险和CDS投资策略
Robust Optimal Proportional Reinsurance and CDS Investment Strategies for Insurer with Jump-Diffusion Risk[J]. 应用数学进展, 2021, 10(03): 763-773. https://doi.org/10.12677/AAM.2021.103084
参考文献
- 1. Yang, H.L. and Zhang, L. (2005) Optimal Investment for Insurer with Jump-Diffusion Risk Process. Insurance: Mathematics and Economics, 37, 615-634. https://doi.org/10.1016/j.insmatheco.2005.06.009
- 2. Cao, J., Peng, X.C. and Hu, Y.J. (2016) Optimal Time-Consistent Investment and Reinsurance Strategy for Mean-Variance Insurers under the Inside Information. Acta Mathematicae Applicatae Sinica, 32, 1087-1100.
https://doi.org/10.1007/s10255-016-0629-y
- 3. Promislow, S.D. and Young, V.R. (2005) Minimizing the Probability of Ruin When Claims Follow Brownian Motion with Drift. North American Actuarial Journal, 9, 109-128. https://doi.org/10.1080/10920277.2005.10596214
- 4. Wang, N., Zhang, N., Jin, Z. and Qian, L.Y. (2018) Robust Non-Zero-Sum Investment and Reinsurance Game with Default Risk. Insurance: Mathematics and Economics, 84, 115-132. https://doi.org/10.1016/j.insmatheco.2018.09.009
- 5. Zhao, H., Shen, C.Y. and Zeng, Y. (2019) Robust Equilibrium Excess-of-Loss Reinsurance and CDS Investment Strategies for a Mean-Variance Insurer with Ambiguity Aversion. Insurance: Mathematics and Economics, 88, 159-180.
https://doi.org/10.1016/j.insmatheco.2019.06.007
- 6. Zeng, Y., Li. Z. and Lai, Y. (2015) Time-Consistent Investment and Reinsurance Strategies for Mean-Variance Insurers with Jumps. Insurance: Mathematics and Economics, 52, 498-507.
https://doi.org/10.1016/j.insmatheco.2013.02.007







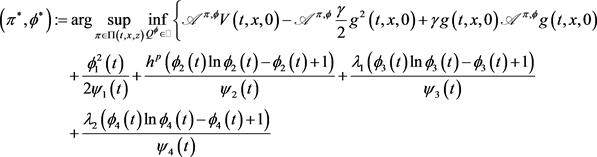 (26)
(26)



