Computer Science and Application
Vol.
09
No.
11
(
2019
), Article ID:
33083
,
10
pages
10.12677/CSA.2019.911236
Predict Model for Foreign Exchange Expenditure Based on Optimized Grey-Markov
Qingzheng Wei, Yun Yang, Lingyan Li
College of Information Engineering, Yangzhou University, Yangzhou Jiangsu
Received: Nov. 1st, 2019; accepted: Nov. 14th, 2019; published: Nov. 21st, 2019

ABSTRACT
Based on the grey prediction, and Markov model, the Grey-Markov prediction model is proposed in the paper. Then PSO is used to optimize the parameters and improve the prediction accuracy. Combining grey model and Markov model, the trend of time series data is obtained by grey model. Markov model makes the data show volatility, to obtain the time series trend prediction. By verifying the data on the foreign exchange expenditure business volume, the results show that the combined prediction model of PSO can not only get the general trend of time series, but also make the data show the volatility with time, and improve the prediction accuracy. The accuracy of the optimized combined forecasting model is higher than that of the single forecasting model.
Keywords:GM(1,1), Markov Model, PSO, Foreign Exchange Expenditure, Combined Prediction
优化的灰色马尔科夫外汇支出预测模型
魏庆征,杨 云,李凌燕
扬州大学信息工程学院,江苏 扬州
收稿日期:2019年11月1日;录用日期:2019年11月14日;发布日期:2019年11月21日

摘 要
本文以灰色预测为基础,结合马尔科夫模型,建立灰色马尔科夫预测模型。然后使用粒子群算法对参数进行优化,提高预测精度。将灰色模型和马尔科夫模型组合,用灰色模型得到时间序列数据的趋势,用马尔科夫模型使数据呈现出波动性,得到时间序列趋势预测。通过对外汇支出业务量的数据进行验证,结果表明:粒子群优化的组合预测模型即可得到时间序列数据的总体趋势,又可以使数据随着时间的变换呈现出变换的波动性,提高预测精度。优化的预测组合预测模型精度高于单一预测模型的精度。
关键词 :GM(1,1),马尔科夫模型,粒子群,外汇支出,组合预测

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
预测是各国专家学者致力于研究的问题,根据各学科领域的不同,也提出了许多预测方法,时间序列分析法,回归分析法,神经网络预测法,灰色预测法和马尔科夫预测等。相比于其它预测模型,灰色预测模型所需要的数据量小等优点,但是对于具有随机波动性的数据,灰色预测呈现出预测精度低等问题 [1]。随着组合预测模型的提出 [2],有效地提高了预测的精度。本文使用组合的灰色马尔科夫预测模型,并通过粒子群算法对其进行优化。以某市外汇业务支出量对模型进行验证。
2. 相关工作
2.1. 灰色GM(1,1)预测模型
灰色系统理论是由我国邓聚龙教授于20世纪80世纪初提出,已广泛应用于社会、经济、科技、农业、生态、生物等各个领域 [3]。其中GM(1,1)模型是灰色系统理论的核心模型。该模型是由一个变量的一阶微分方程构成。
设原始序列为 ,并且序列中的任何一项均不为负数。其中 。
对原始序列进行级比计算:
(2.1)
进而得到级比序列
计算级比检验区间 :
(2.2)
判断级比是否落入检验区间,如果未落入,则对原始序列进行相应的数据变换,常见的变换方式:对数变换,方根变换和平移变换。对变换后的数据序列进行一次累加生成(AGO),即将同一序列中数据逐次相加以生成新的数据。
即 ,其中:
(2.3)
GM(1,1)的一阶线性微分方程为:
(2.4)
其中a为发展系数,a的大小和符号反应了 和 的发展态势,b为灰作用量。a和b可以通过最小二乘法求得。
(2.5)
Y为数据向量:
(2.6)
B为构造矩阵,形式如下:
(2.7)
于是得到预测模型:
(2.8)
通过递减得到GM(1,1)预测模型的还原值:
(2.9)
2.2. 灰色马尔科夫模型
马尔科夫链是由俄国数学家马尔科夫提出,是一种时间离散状态的马尔科夫过程。未来状态的发生概率仅和当前系统状态有关,与系统过去状态无关。马尔科夫过程是根据现在的状态和状态转移概率,预测未来可能出现的状态 [4]。
2.2.1. 状态区间的划分
通过GM(1,1)预测模型,计算真实值和预测值之间的相对误差,通过相对误差的范围进行状态区间的划分。状态区间为:
其中 分别为状态区间的上下限 [5]。
2.2.2. 状态转移概率矩阵
设序列 在时间t的状态为 的概率为 ,若序列 从 状态转移到下一个时间状态 的概率为 ,则 为从时刻t处于i状态到下一个时刻 转移到j状态的概率。满足此条件的时间序列为马尔科夫链。 为在t时刻的一步转移条件概率 [6]。
由概率组成的矩阵称为概率矩阵。状态 转移到状态 的次数为 ,状态 的总次数为 ,状态 到状态 的概率为 。
,,
k步转移概率为:
所以k步转移概率矩阵为k步转移概率组成的矩阵。形式如下:
矩阵具有如下两个性质:
① 非负性: ;
② 行元素和为1,即 。
根据当前时刻所处的转态,利用一步转移概率矩阵对下一时刻进行预测。
当前时刻t的状态为 ,则 时刻转移到状态 ,状态j出现的概率最大,则为下一时刻的预测结果 [7]。
2.2.3. 计算灰色马尔科夫预测值
(2.10)
2.3. 粒子群算法对灰色马尔科夫预测模型的优化
2.3.1. 粒子群算法
粒子群算法(Particle Swarm Optimization, PSO)是一种仿生物集群进化算法,PSO由美国科学家James Kennedy和Russell Eberhart于上世纪90年代提出 [8]。
PSO算法首先初始化一群随机粒子,通过对局部最优解和全局最优解的不停迭代以得到最终结果。在迭代的过程中,粒子通过参考个体极值(pbest)和全局极值(gbest)来更新自己。粒子没有质量和体积,但是有自己的位置和速度,粒子的速度代表飞行的方向和距离,位置代表空间中的一个点。在一个D维搜索空间,N个随机粒子的群体中,第i个粒子的空间位置为 ,速度为 。在粒子探索的过程中,个体极值(pbest)为粒子个体本身所达到的最优值即局部极值用 表示,全局极值(gbest)为粒子在整个种群中所能达到的最优值用 表示。粒子根据个体极值和全局极值,按照以下两个公式不断更新自身的速度和位置 [9] [10]。
(2.11)
(2.12)
其中 和 为随机数,取值范围为[0, 1], 和 为学习因子,通常 , 的作用是提高算法的收敛速度。 代表飞行过程中自身影响。 代表飞行过程中全局影响。 代表粒子个体极值在d维分量所经历的最好位置, 代表粒子全局极值在d维分量所经历的最好位置, 为粒子所在位置的第d维分量, 为粒子速度的d维分量。w为惯性权重,上一速度对当前速度的影响。w过大,算法的全局搜索比较好,w过小,局部搜索能力加强。
2.3.2. 粒子群算法实现的步骤 [11]
步骤① 设定粒子数目,并进行初始化,随机生成初始速度。
步骤② 每个粒子的速度和位置都是在持续更新,在当前时刻具有最新的位置,计算粒子的目标函数fitness。
步骤③ 计算粒子的适应值,如果优于原有的个体极值,则用当前适应值替换原有的个体极值。
步骤④ 根据粒子的个体极值寻找全局极值。
步骤⑤ 根据式(2.11)改变粒子速度,每个粒子都不可以超过最大速度,如果超过,则该粒子的速度会被设定为最大速度。
步骤⑥ 根据式(2.12)更新粒子的位置。
PSO算法流程图见图1所示:

Figure 1. PSO algorithm flow chart
图1. PSO算法流程图
2.4. 模型检验
模型对于预测的效果,需要根据模型的评定指标进行检验,我们这里采用2个误差标准作为模型的评定指标。
① 平均绝对误差
其值越小越好,反映了模型预测值和原始值的平均偏离程度。
② 平均绝对百分误差
其值越小越好,反映了不同模型对相同数据拟合好坏的比较。
为误差,即预测值和原始值的误差。 为原始值。
3. 实验分析
以某市2017年度个人外汇涉外支出业务量作为原数据(2017.01~2017.12),建立GM(1,1)模型:
对数据进行检验,按式(2.1)计算级比:
计算级比检验区间范围为:
发现级比 的值不完全落在检验区间范围内,需要对原数据进行相应的变换,如平移变换,方根变换,对数变换,这里我们选择平移变换,平移量C = 150,平移后的数据为:
从而再次得到级比:
发现新的级比 往前落在检验区间(0.857, 1.166)。
根据式(2.3)生成一次累加数据:
根据式(2.6)和式(2.7),构造数据向量Y和矩阵B,计算参数a和b的值
得到式(2.4)对应的微分方程
对应式(2.8)的预测模型为:
由式(2.9)我们可以还原数据,在还原数据之前,由于我们对原始数据做了平移,所以要减去平移量C = 150,所以最终的还原数据见表1所示。
Table 1. Comparison between GM(1,1) model and Grey-Markov model
表1. GM(1,1)模型与灰色–马尔科夫模型预测值对比
通过GM(1,1) 预测模型得到2018.1和2018.2的外汇支出业务量的预测值分别为:1070和1029。
由表1可知,GM(1,1) 预测模型的相对残差范围为(−19.1, 9.8),所以我们根据相对残差范围进行状态区间的划分,划分的状态区间分别为:E1(−20, −6],E2(−6, −2],E3(−2, 0),E4[0, 3],E5(3, 5],E6(5, 10]。最终划分结果见表2所示。
Table 2. Division of Markov interval states
表2. 马尔科夫区间状态划分
得到的灰色马尔科夫预测结果见表1所示。根据状态划分进行状态矩阵的构建,得到一步转移概率矩阵和两步转移概率矩阵。
,
由于12月份所处的状态为E3,所以初始状态向量为(0, 0, 1, 0, 0, 0),根据初始向量状态和一步转移概率矩阵、两步转移概率矩阵得到2018年1月和2月的概率预测见表3所示。
Table 3. 2018.1-2018.2 Probability
表3. 2018.1~2018.2概率
于是得到2018年1月和2月的灰色马尔科夫预测结果分别为1113和1162。
预测结果对比见图2所示:

Figure 2. Comparison between GM(1,1) and GM(1,1)—Markov model
图2. GM(1,1)与GM(1,1)——马尔科夫模型对比
下面通过粒子群算法对灰色马尔科夫模型中的参数进行优化,计算灰色马尔科夫模型中区间的白化系数。设白化系数为 。选取m个粒子构成粒子群,粒子的长度为d,即粒子为d维向量,这个向量代表白化系数 。白化系数初始值为随机生成,区间范围为[0, 1]。进行初始化后,粒子的位置根据飞行速度的变换而变换,本文用均方差衡量粒子的适应度函数值。
根据马尔科夫的状态区间 ,我们在灰色马尔科夫模型中的白化系数取值 ,即 。在实际情况中取值不一定是中间值,所以我们通过粒子群算法计算出最优的白化系数值。
在粒子群算法中,我们根据一步概率转移矩阵和已经划分好的6个状态区间,我们选择粒子的长度为6,粒子数为1000,学习因子 ,惯性权重为1,迭代次数1000,粒子更新位置最大为1,最小为0,粒子更新速度最大为0.01,最小速度为−0.01。从而得到白化系数。
进而得到粒子群灰色马尔科夫模型对外汇支出的预测值,见表4所示,预测结果对比图见图3所示,误差对比见表5所示。
Table 4. Prediction value of Grey Markov model based on PSO
表4. 粒子群优化灰色马尔科夫模型预测值
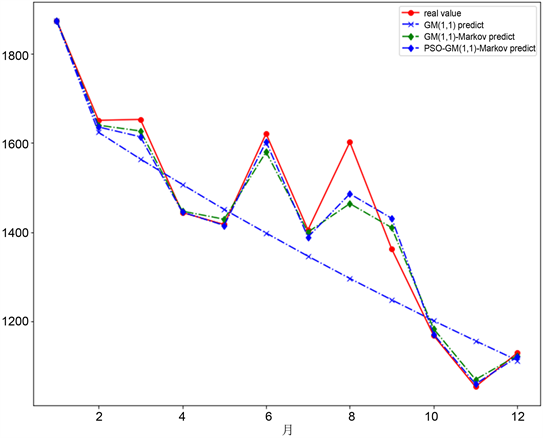
Figure 3. Grey-Markov prediction and PSO Grey-Markov prediction model
图3. 灰色马尔科夫预测模型和粒子群优化的灰色马尔科预测模型
Table 5. Comparison of prediction model error
表5. 预测模型误差对比
从上表可以看成,粒子优化的灰色马尔科夫预测模型在一定程度上优于灰色马尔科夫模型,我们通过粒子群优化的灰色马尔科夫预测模型得到2018.1和2018.2的外汇支出业务量的预测值分别为:1104和1180。
4. 结束语
本文首先采用灰色预测模型得到一个预测趋势,但不能反映出数据的随机波动性,然后结合马尔科夫链进行组合预测,使数据呈现出较好的随机波动性,接近原始数据,提高预测的精度。接着,我们再通过使用粒子群算法对灰色马尔科夫预测模型进行参数优化,进一步提高预测精度,达到更加接近真实值的效果。也体现出组合预测模型比单一预测模型精度高,效果更好。
基金项目
江苏省产学研前瞻性联合项目(BY2016069-16)
文章引用
魏庆征,杨 云,李凌燕. 优化的灰色马尔科夫外汇支出预测模型
Predict Model for Foreign Exchange Expenditure Based on Optimized Grey-Markov[J]. 计算机科学与应用, 2019, 09(11): 2105-2114. https://doi.org/10.12677/CSA.2019.911236
参考文献
- 1. 张大海, 汪世芳, 史开泉. 灰色预测公式的理论缺陷及改进[J]. 系统工程理论及实践, 2002, 22(8): 140-142.
- 2. Bates, J.M. and Granger, C.W.J. (1969) The Combination of Forecasts. Journal of the Operational Re-search Society, 20, 451-468. https://doi.org/10.1057/jors.1969.103
- 3. 邓聚龙. 灰理论基础[M]. 武汉: 华中科技大学出版社, 2002: 222.
- 4. 郭书坡. 基于灰色马尔科夫链的优化模型及其在茶叶产量预测中的应用[D]: [硕士学位论文]. 兰州: 兰州大学, 2011.
- 5. 陈焕珍. 基于灰色马尔科夫模型的青岛市粮食产量预测[J]. 计算机仿真, 2013, 30(5): 429-433.
- 6. 高蔚. GM-Markov综合模型在汽车货运量预测中的应用[J]. 机械设计与制造, 2011(8): 63-65.
- 7. 程恒. 粒子群—灰色马尔科夫链的改进及应用[D]: [硕士学位论文]. 黄石: 湖北师范大学, 2016.
- 8. Kennedy, J. and Eberhart, R.C. (1995) Particle Swarm Optimization. IEEE International Confer-ence on Neural Networks, 4, 1942-1948.
- 9. Shi, Y. and Eberhart, R. (1998) A Modified Particle Swarm Optimizer. In: Proceedings of the IEEE International Conference on Evolutionary Computation, IEEE Press, Piscataway, NJ, 69-73.
- 10. 张丽平. 粒子群优化算法的理论及实践[D]: [博士学位论文]. 杭州: 浙江大学, 2005.
- 11. 樊冬雪. 基于优化灰色马尔科夫链模型的铁路客流量预测方法研究[D]: [硕士学位论文]. 重庆: 重庆交通大学, 2015.
