Hans Journal of Civil Engineering
Vol.
12
No.
03
(
2023
), Article ID:
63386
,
13
pages
10.12677/HJCE.2023.123041
基于马尔科夫决策过程的轨道状态维修决策
赵文博
中国铁道科学研究院集团有限公司基础设施检测研究所,北京
收稿日期:2023年2月29日;录用日期:2023年3月21日;发布日期:2023年3月30日

摘要
本文根据自然劣化情况下的轨道几何特征数据进行聚类分析,以形成的簇类为决策单元构建完整环境下的马尔科夫决策模型,以最大化轨道运行长期期望利润为目标,优化铁路维修决策过程。首先,基于轨道不平顺数据的变化特征,对照高速铁路实际运行里程和地形特征,以函数型聚类的思想对不同区段下轨道时序数据进行预处理,并采用K-Means++的方法对轨道几何变化特征进行聚类,形成多个独立的决策单元,以增强后续决策建模的科学性。其次,采用马尔科夫过程来描述轨道质量状态变化并建立轨道状态转移概率矩阵,简化铁路运行收入和维修养护成本,以建立利润模型,基于轨道日常维修养护措施建立决策动作模型,以不同决策单元的TQI数据为基础构建完整环境下的马尔科夫决策模型。最后,基于某高速铁路轨道数据进行数值实验,采用值迭代法求解马尔科夫决策模型,使得高速铁路运行的长期期望利润最大化,确定不同轨道状态下的最优维护决策,以达到减少维修成本、优化维修决策的目的,对现行铁路维修养护工作起到一定的实际指导意义。
关键词
轨道状态维修,数据分析,K-Means聚类,TQI,马尔科夫决策

Track Condition Maintenance Decision Based on Markov Decision Process
Wenbo Zhao
Infrastructure Inspection Research Institute, China Academy of Railway Sciences Co., Ltd., Beijing
Received: Feb. 29th, 2023; accepted: Mar. 21st, 2023; published: Mar. 30th, 2023

ABSTRACT
In this paper, cluster analysis is carried out based on the geometric feature data of the track under natural deterioration, and a Markov Decision Process model under a complete environment is constructed by taking the formed cluster class as a decision unit. In order to maximize the long-term expected profit of track operation as the goal, the decision-making process of railway maintenance is optimized. Firstly, based on the various characteristics of track irregularity data and the actual running distance and terrain characteristics of high-speed railways, the track timing data under different sections were preprocessed by the idea of functional clustering. Moreover, the K-Means++ method was used to cluster the geometric variation characteristics of the track, forming multiple independent decision units to enhance the scientific nature of subsequent decision modeling. Secondly, the Markov process is used to describe the change in track quality state and establish the probability matrix of track state transfer to simplify the railway operating income and maintenance cost, so as to establish the profit model. The decision action model is established based on the daily maintenance measures of the track, and the Markov Decision Process model under the complete environment is built based on the TQI data of different decision units. Finally, based on the track data of a high-speed railway, the numerical experiment is carried out, and the value iteration method is used to solve the Markov Decision Process model, which maximizes the long-term expected profit of high-speed railway operation and determines the optimal maintenance decision under different track states, so as to reduce the maintenance cost and optimize the maintenance decision, which plays a certain practical guiding significance for the current railway maintenance work.
Keywords:Track Condition Maintenance, Data Analysis, K-Means Clustering, TQI, Markov Decision Process

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
铁路运营过程中,轨道质量会随着使用时间不断劣化,发生事故的概率逐渐增加。在我国铁路“六次大提速”的背景下,快速化、重载化的列车运行加剧了轨道状态的劣化,使得需要的维修和检测频次增加,但是单纯地增加检测频次会造成资源浪费,带来过高的运行成本,因此需要提高轨道质量检测和维护的方式科学性。
现行轨道几何状态的评定和验收标准多采用动态评定的方法,利用综合检测列车测量轨道几何状态,包括高低、轨向、轨距等项目,每次检测完成后,综合检测车会自动形成轨道线路的原始检测数据、各检测项目的超限报表以及每200 m长度的TQI数据等结果,提供给铁路工务部门进行分析使用。工务部门利用检测结果来管理评价轨道,主要有两种方法:轨道几何高低、轨向等局部幅值分级超限评价方法(局部峰值管理);对200 m单元区段内轨道几何高低、轨向、轨距、水平、三角坑等七项指标构建轨道质量指数(TQI)进行综合评价(区段均值管理)。
根据轨道线路劣化状况,工务部门采取针对性养护维修措施。目前,国内主要的轨道养护管理方法有两种模式:工务部门根据综合检测列车检测发现的轨道几何尺寸超限处所,以及TQI较差的区段编制具体维修计划,即“故障修”;当轨道线路累积通过的总重量超过规定的标准且轨道部件存在较多的病害问题时,安排相应的大中修或综合维修计划,即“周期修”。这两种轨道养护管理模式大幅增加了工务部门的工作量,同时对于有限的养护维修资源,如资金、养护机械等,无法做到合理安排以及科学配置,最后造成大量的资源浪费,耽误工作效率。
近些年,为了节约资源,提高效率,各行业针对工业部件老化,纷纷提出了另一种养护维修模式,即“状态修”。其中,一个最重要的内容就是根据工业部件的实际质量状态建立维修决策模型,从而可以针对当前状态做出维修决策,实现对“零误差”管理。国内外已有不少研究者将马尔科夫决策应用于维修决策的领域。Sancho等 [1] 将马尔科夫决策过程应用到钢轨部件磨削和更新决策上; Kamrani等 [2] 分析了驾驶员不同情形下行为的转移奖励,应用马尔科夫决策过程制定了科学的驾驶决策指导;田雪雁等 [3] 将马尔科夫决策应用到双机系统的维修决策中,制定了系统处于不同状态下的最优决策方案;赵扬 [4] 采用马尔科夫决策模型应用到城市轨道交通的维修决策中去,通过优化的方法求解马尔科夫决策模型,从而指导城市轨道的维修决策。
随着我国铁路运营速度的提高,“严检慎修”理念和“全面测量、综合分析、细化方案、精细修理”的作业原则对工务设备的检测、维修和养护管理提出了更高的要求,“状态修”的理念正符合当前的轨道管理要求。因此,本文借助工务部门广泛采用的反映轨道质量状态的TQI评价指标,引进“状态修”的理念,首次尝试将马尔科夫决策模型应用到高速铁路轨道不平顺的维修中。
2. 轨道几何状态特征
2.1. 轨道状态评价指标
轨道几何不平顺的评价主要通过采用统计特征值指标的方法使轨道区段内所有测点的检测值都参与到运算中,铁路工务部门普遍采用的轨道质量指数(TQI)作为一项统计特征值可以在一定程度上反映轨道区段整体不平顺状态及轨道恶化程度。
TQI以200 m长度轨道区段作为计量单元,对单元内的轨道几何进行统计,用标准差来表示单项轨道几何不平顺状态,而TQI则为一个单元内左高低、右高低、左轨向、右轨向、轨距、水平和三角坑等七项几何不平顺标准差之和,计算见公式:
(1)
(2)
(3)
2.2. 数据预处理
由于检测过程中受到电磁干扰或是检测日当天的气候原因,检测设备可能会得到一个异常数据,具体表现为当次检测得到的数值和邻近几次检测得到的数值有巨大的差异。本文以变化较为明显的高低标准差为例进行分析,构造高低标准差时间序列,结果如图1所示,可以发现含有明显异常值。
首先需要去除噪声值,保证时间序列质量。采用S-H-ESD方法检测数据异常值,S-H-ESD方法是利用STL将时间序列数据分解为趋势项、周期项和余项 [5] ;然后对余项应用ESD方法,并将ESD方法中的均值与标准差替换为中位数与绝对中位差来消除个别异常值对样本的均值和标准差的较大影响,同时由于原始数据采样的间隔周期并不规律,为了保证数据的一致性,本文对原始数据以每月采样一次的频率对原始数据重采样。对于缺失的点,用邻近点的线性插值来填补,得到的结果如图2所示。
2.3. 时间序列特征分析
2.3.1. 维修特征
由于高速铁路轨道在不同道路区段所处的自然环境、路基条件、行驶速度不同,轨道几何指标的变化特征不同,如图3所示。轨道质量状态自然劣化的转移概率存在里程上的差异,如果将所有轨道数据

Figure 1. Schematic diagram of abnormal time series
图1. 异常时间序列示意图
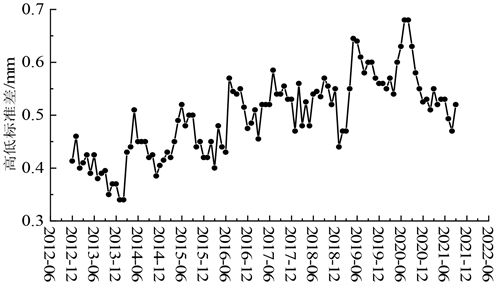
Figure 2. Time series after noise reduction and interpolation
图2. 降噪和插值后时间序列
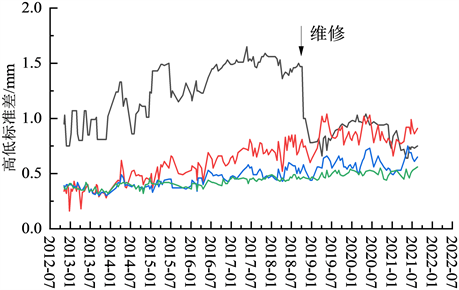
Figure 3. Variation trend of high and low standard deviation of track in different sections
图3. 不同区段轨道高低标准差变化趋势
进行统一分析,会影响模型决策的科学性和准确性。
本文首先利用函数型聚类方法,按照轨道不平顺几何指标的时间变化特征对轨道区段进行聚类分析,将轨道划分为多个决策区段 。由于TQI是水平、左高低、右高低、左轨向、右轨向、三角坑和轨距7项标准差的加和,结合实际运维经验,在不影响分类效果的前提下,本文选用比较具有代表性的高低标准差作为分析分类的依据。
由于不同铁路线路,或者同一条线路的不同区段的轨道数据特征多变,直接分类可能会导致类别过多,使得分类的效果并不明显,因此本文将轨道区段进行预分类,采用Shapelet方法区分是否维修 [6] 。
若某个区段的轨道在近年来已被维修过,那么该区段的高低标准差数据会有明显的“断崖式下跌”特征。这类子序列是所有已维修区段都具有的代表性特征,如图4所示。因为维修带来的特征并不是全局的,而是一种局部的特征,可以考虑使用半监督的分类方法Shapelet来区分维修区段和未维修区段。

Figure 4. Track irregularity trend in some maintenance sections
图4. 部分维修区段轨道不平顺趋势
Shapelet方法是一种半监督学习分类方法,该方法的分类依据为训练集中具有代表性特征的子序列(以下简称特征子序列)。若待分类的数据集中具有一段和已知特征子序列匹配的子序列,那么就认为该数据集和相匹配的特征子序列属于同一类数据,从而达到分类的效果。如果在测试集上的区分效果,如表1所示。
Table 1. Distinguish effect of Shapelet method
表1. Shapelet方法区分效果
2.3.2. 聚类结果分析
用聚类方法进一步分析未维修区段。在区分了未维修区段、已维修区段后,轨道数据不再具有明显的、极具代表性特征的子序列。为了更好地发掘区段具有的其它潜藏特征,选用无监督的K-Means++的聚类方法进行聚类分析,算法步骤如下:
a) 从输入的数据点集合中随机选择一个点作为聚类中心 ;
b) 对于数据集中的每一个点 ,计算它与已选择的聚类中心中最近聚类中心的距离 ;
c) 选择一个新的数据点作为新的聚类中心, 越大的点,被选取作为聚类中心的概率越大;
d) 重复b)、c)直到选出k (事先确定)个聚类中心。
用K-Means++的聚类方法对未维修区段的部分聚类结果,如图5所示,簇1表现为高低标准差周期性劣化发展趋势;簇2表现为高低标准差平稳发展趋势;簇3表现为高低标准差近似线性发展趋势;簇4表现为轨道劣化严重经过维修整治后高低标准差改善明显。
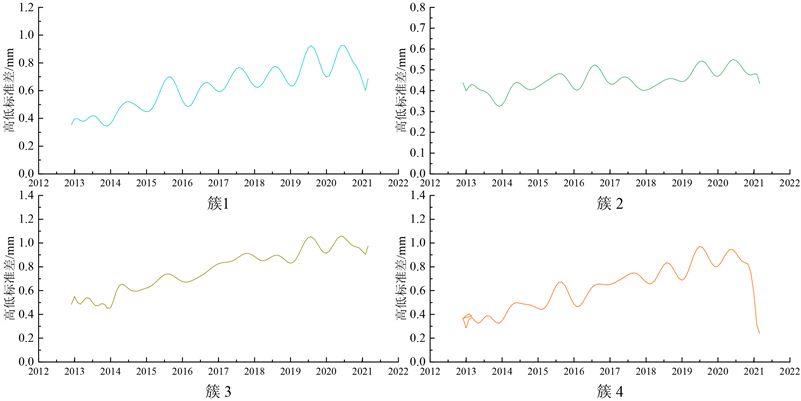
Figure 5. K-Means data after clustering method
图5. K-Means聚类方法后的数据
2.3.3. 聚类效果评价
通过轮廓系数和Davies-Bouldin指数两种性能评估方法对前文的不同分类个数聚类性能进行评估 [7] ,并结合实际因素选择恰当的聚类簇数,如表2所示。
Table 2. Evaluation index under different classification cluster number
表2. 不同分类簇数下的评价指标
1) 使用轮廓系数进行评价:轮廓系数代表各簇类的“不相似度”。
2) Davies-Bouldin指数:该指数表示集群之间的平均“相似度”。
两种评估方式得到的数据都说明,各簇的“相似度”一定程度上随着簇数的增多而增加,但是又由于簇设置过少将影响整体区分效果,所以应根据实际效果选择合适的分类簇数。本文将全部的轨道数据按照变化特征分为: 共六个簇,即六个决策单元,为了简化过程,后文中默认对其中一个决策单元进行马尔科夫决策建模分析和数值实验。
3. 马尔科夫决策模型
3.1. 马尔科夫决策模型概述
传统铁路运行维护评价分为局部峰值和区段均值方法,其只考虑轨道的几何状态来制定维修决策,需要以周期性的维修作为支撑。本文在此基础上,依据传统轨道几何状态评定标准的经验,将轨道质量状态按TQI的大小区间分为“好、较好、中、较差、差”五个离散状态,分别用数字1~5表示,记作状态空间 。
高速铁路的维修动作总体上可以分为“检养修”三个部分:定期检查、保养和维修。实际操作过程则具体细分为钢轨、轨枕、道床等的养护与维修。本文将所有的维修与养护措施综合性的简化考虑为“保养、维修”两个动作。用数字0表示不维修,1表示保养,2表示维修,这样动作空间可以定义为 。以此为基础来构建离散状态的马尔科夫决策模型。
马尔科夫决策过程(Markov Decision Process,简称MDP)是序贯决策的数学模型,也是强化学习的经典模型之一。进入20世纪80年代后,人们对MDP的认识逐渐从“系统优化”转为“学习”。英国学者Chris Watkins首次在强化学习中尝试使用MDP建模。
在一个强化学习过程中,agent和environment的交互,在每个时间t,agent基于状态s,做出动作a,获得reward R,之后进入下一个阶段,从而形成了一个序列:
(4)
本文的目标是通过恰当方法求解该序列。由于马尔科夫过程具有未来状态的条件概率分布仅依赖于当前状态的性质,因此将序列过程抽象为马尔科夫过程可以有效地简化这一序列的求解。现在马尔科夫决策过程(MDP)已作为求解最优策略问题的重要模型获得了广泛的应用。本文将轨道质量状态转移过程视作马尔科夫过程,构建完整环境下的MDP,并采用动态规划的方法进行MDP的求解。
完整的MDP由五元组组成: ,考虑单个决策单元:
S:状态空间。根据轨道几何特征指标的区间,划分离散状态空间 ,分别代表“好、较好、中等、较差、差”五个离散的轨道质量状态。
A:动作空间。在实验中预设动作空间 ,分别代表“不维修、保养、维修”三个动作,同时将agent在特定环境下针对不同轨道状态采取的动作集记为策略 。
P:状态转移矩阵。通过统计原始轨道状态之间转移的频率来估计转移概率,构建状态转移矩阵。
R:回报矩阵。从某一状态转移到下一状态前所能获得的回报,定义为从该状态转出即可获得回报。通过维修成本和铁路运行收益定义,影响最终决策结果。针对一条完整的转移路径,获得的路径回报为 。
:折扣因子。用于定义初始状态对后续状态的影响大小的参数。
为了方便模型求解并保证决策模型的科学性,本文做出以下几个假设:
(1) 轨道质量状态在自然条件下的转移,近似服从马尔科夫过程。
(2) 铁路正常运营条件下,每周期获得的利润不变。
(3) 轨道的维修和保养服从几何分布,维修成功率随轨道质量的降低而降低,且轨道维修期间不存在运行利润,维修成本随轨道质量状态的劣化而提高。
(4) 轨道维修在维修和保养成功后只会转移到最优状态,维修和保养不成功则保持原状态。
(5) 铁路运行收入随铁路质量状态的下降而减少。
3.2. 状态转移模型
用P表示轨道质量的状态转移概率矩阵,则轨道质量状态在相邻两个转移周期,从状态i转移到状态j的概率记作 , ,在数据样本足够大的情况下,用轨道质量状态转移的频率估计转移概率 。在引入维修动作后,在每一个轨道状态,agent均可采取三种决策动作 ,分别代表不维修,保养和维修。综上,状态转移矩阵模型记为: ,其中 , ,转移模式如图6所示。
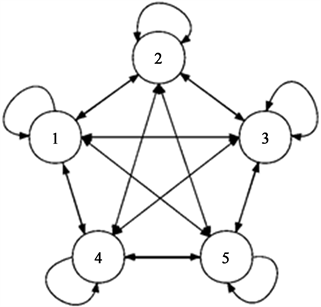
Figure 6. State transition procedure
图6. 状态转移过程
基于假设(3),将轨道在当前周期进行保养,下一周期完成保养的概率用 表示,且 随轨道质量下降而下降,根据假设(4),保养完成后只会转移到最优状态,保养未完成则保持原状态。同理,维修成功的概率用 表示,转移概率及状态转移模式与保养动作相同。
那么当系统处于状态 ,采取动作 时,下一周期转移到j状态的概率分为以下几种情况:
1) 不采取任何动作,轨道在自然状态下转移的概率为:
, (5)
2) 在本周期采取保养动作,下一周期保养成功结束的概率为:
, (6)
3) 本周期采取保养动作,下一周期保养未结束的概率为:
, (7)
4) 本周期采取维修动作,下一周期维修成功结束的概率为:
, (8)
5) 本周期采取维修动作,下一周期维修未结束的概率为:
, (9)
3.3. 利润模型
基于假设(2),用r表示铁路最优条件下运行的收益,为一个常数, 表示在不同轨道状态下的自然收益损失,轨道质量状态越差 越高; 表示铁路的保养成本,保养成本随轨道状态质量的下降而增高,在保养进行时铁路仍存在运行收益;采取维修动作时铁路运行收益为0,用c表示不同轨道状态的下的维修成本,为了简化铁路利润模型,所有参数均表示在单位周期下的情况。最终利润函数采用收入与成本之差定义如下:
1) 轨道在自然状态下的利润函数为:
(10)
2) 轨道在采取保养动作时的利润函数为:
(11)
3) 轨道在采取维修动作时的利润函数为:
(12)
3.4. 价值函数
价值函数: ,表示从状态s出发,在策略 下,经过所有路径的回报的期望值。代入路径回报函数: 后,进一步可以化简为:
(13)
引入动作之后,动作价值函数 代表从状态s出发,采取动作a后,再使用策略 所获得的回报,即动作价值函数:
(14)
同时,有动作价值函数与价值函数的关系:
(15)
并且由最优策略 的定义:
(16)
可以推导出最优价值函数:
(17)
与最优动作价值函数:
(18)
相结合得到公式:
(19)
(20)
上述关于最优值函数的等式,称为最优Bellman方程,其唯一解是最优值函数,想要知道 、 ,就要先知道 、 ,很显然,这是一个递归过程,计算所有初始状态采取不同动作下的最优价值函数来决定最优决策。
3.5. 长期期望利润模型
为保证模型在较长周期下收敛,取任意折扣因子 ,则模型的长期期望利润满足:
(21)
由上一节公式,长期期望利润函数还可以定义为:
(22)
那么,展开定义不同状态下的动作价值函数,并计算最优策略。在轨道状态为1时,采取不同动作下的价值函数为:
(23)
(24)
(25)
轨道状态为2时:
(26)
(27)
(28)
轨道状态为3时:
(29)
(30)
(31)
状态4、5下的价值函数同1、2、3,通过计算上述公式,最大化长期价值函数,即可得到在不同状态下最优的决策动作。
4. 案例分析
4.1. 数值迭代
令 表示迭代周期,采用值迭代法来计算较长周期的折扣值函数直至收敛。Bellman等式是值迭代算法的理论基础 [8] 。
(32)
值迭代算法具体步骤如下:
步骤1:初始化,对于任意系统状态 ,设置 ,令 ,取任一 ;
步骤2:对于每一个状态计算 ;
步骤3:若 ,则进入步骤4,否则另 ,返回步骤2;
步骤4:输出各状态下,不同决策值函数。
比较不同动作值函数的值,计算最优价值函数(动作值函数)得到较长周期的最优策略。
4.2. 案例计算
本文采集了某高速铁路其中一个决策单元共73,960个数据。对照设计速度表,该单元数据90%集中在350 km/h速度等级区段,使用TQI在不同轨道状态下转移的频率来估计状态转移概率,根据轨道几何状态动态检测及评定标准划分5个轨道状态区间,得到状态转移概率矩阵的结果如表3所示。
Table 3. State transition probability matrix
表3. 状态转移概率矩阵
在得到轨道状态间的状态转移概率矩阵之后,采用值迭代法进行数值实验。共针对四个算例进行优化求解,并输出最优维修决策:
1) ;
2) ;
3) ;
4) 。
所有算例的参数设置均满足本文假设(2)、(3)、(5),得到的最优维修策略如下表4所示。
Table 4. Optimal actions of different examples in each state
表4. 不同算例在各个状态下的最优动作
以算例1为对照,1、3、4三个算例分别降低了维修成本,提高了维护成本以及降低了铁路状态差时的风险成本。以算例2为例,对照算例1可以看到,当提高维护成本时,使agent采取维护决策的倾向性降低,在轨道状态为3时,维护成本高于铁路自然劣化的风险成本,实际决策为不采取维护动作而采取保养动作,待轨道质量状态进一步劣化为4状态时直接采取维修决策;算例3对照算例2,则表示当保养的风险成本较高时,在状态3时选择直接跳过保养动作采取维护动作;算例1则表示在维修成本降低之后,agent会更轻易地采取维修决策;算例4则表示铁路自然劣化的风险成本较低时,可以延后进行维修决策。
将算例4的实验结果应用到同样决策单元的一条实际铁路区段,得到的一条具体的铁路维修决策如图7所示。
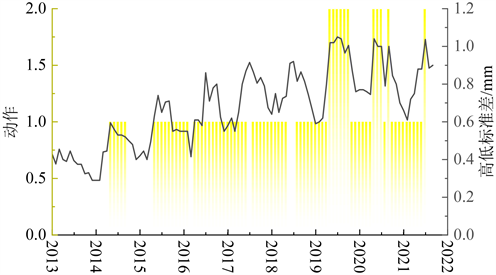
Figure 7. A long-term track maintenance strategy for a unit section
图7. 某单元区段的较长时期的轨道维修策略
5. 结论
本文结合轨道几何劣化状态及维修情况建立了基于马尔科夫决策过程的轨道状态维修决策模型,得出如下结论:
1) 采用轨道几何指标TQI构建时间序列模型,可以明显反映轨道不平顺发展趋势,轨道生命周期中的承载、养修等因素都可以通过TQI时间序列展现。
2) 轨道几何发展过程中“养修”是一个重要的步骤,会明显改变TQI的发展趋势,因此将“养修”作为马尔科夫模型的“动作”输入,可以改善决策的效果。
3) 按照运营经验,将轨道质量状态按TQI的大小区间分为“好、较好、中、较差、差”五个离散状态,以四个算例针对实际不同的应用场景进行了维修决策,实验证明,基于马尔科夫方法可以充分考虑轨道状态及运营期间的人为因素影响,制定出了符合经济预期的状态维修策略。
基金项目
中国铁道科学研究院集团有限公司院基金项目(2021YJ259)。
文章引用
赵文博. 基于马尔科夫决策过程的轨道状态维修决策
Track Condition Maintenance Decision Based on Markov Decision Process[J]. 土木工程, 2023, 12(03): 367-379. https://doi.org/10.12677/HJCE.2023.123041
参考文献
- 1. Sancho, L.C.B., Braga, J.A.P. and Andrade, A.R. (2021) Optimizing Maintenance Decision in Rails: A Markov Decision Process Approach. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems, Part A: Civil Engineering, 7, Article ID: 04020051.
https://doi.org/10.1061/AJRUA6.0001101 - 2. Kamrani, M., Srinivasan, A.R., Chakraborty, S., et al. (2020) Applying Markov Decision Process to Understand Driving Decisions Using Basic Safety Messages Data. Transportation Research Part C: Emerging Technologies, 115, Article ID: 102642.
https://doi.org/10.1016/j.trc.2020.102642 - 3. 田雪雁, 王孟雅, 潘尔顺. 基于马尔科夫决策过程的带缓存双机系统不完美维护策略[J]. 上海交通大学学报, 2021, 55(4): 480-488.
- 4. 赵扬. 基于马尔科夫决策过程的城市轨道交通轨道不平顺修理决策优化技术研究[D]: [硕士学位论文]. 北京: 北京交通大学, 2020.
- 5. Blackwell, D. (1962) Discrete Dynamic Programming. The Annals of Mathematical Statistics, 33, 719-726.
https://doi.org/10.1214/aoms/1177704593 - 6. Watkins, C. (1989) Learning from Delayed Rewards. Ph.D. Thesis, Cambridge University, Cambridge, 1-234.
- 7. 孙利荣, 卓伟杰. 函数型聚类分析方法研究[J]. 高校应用数学学报, 2020, 32(2): 127-140.
- 8. Bellman, R.E. (1957) A Markov Decision Process. Journal of Mathematical Mechanics, 6, 679-684.
https://doi.org/10.1512/iumj.1957.6.56038
