Pure Mathematics
Vol.07 No.04(2017), Article ID:21446,15
pages
10.12677/PM.2017.74043
The Focus Properties of Nonsingular Conic Curves in Hyperbolic Plane
Hai He, Youning Wang
School of Mathematical Science, Beijing Normal University, Beijing
Received: Jul. 1st, 2017; accepted: Jul. 15th, 2017; published: Jul. 21st, 2017

ABSTRACT
In the plane geometry, as we all know, the light through a focus of the ellipse is reflected by ellipse to focus on another; similarly the light through the hyperbola one focus, after reflection, reversely focuses on another; and for the parabola it is true that the light from focus is reflected into parallel light. This paper proved that the nonsingular conic curves on the hyperbolic plane have corresponding focus properties; moreover, there are some curves having focusing properties, which are not conic curves.
Keywords:Hyperbolic Plane, Conic Curves, Focus, Beltrami-Klein Coordinate System
双曲平面上非蜕化圆锥截线的聚焦性
何海,王幼宁
北京师范大学数学科学学院,北京
收稿日期:2017年7月1日;录用日期:2017年7月15日;发布日期:2017年7月21日

摘 要
众所周知,在平面几何中,从椭圆一个焦点出发的光线被椭圆反射后汇聚于它的另一个焦点;从双曲线的一个焦点出发的光线被双曲线反射后虚汇聚于它的另一个焦点;而对于抛物线来说,从焦点出发的光线被抛物线反射成为平行光。本文证明了双曲平面上的非蜕化圆锥截线也有相应的聚焦性;而且,存在一些非圆锥截线的曲线,它们也有聚焦性。
关键词 :双曲平面,圆锥截线,聚焦性,Beltrami-Klein坐标系

Copyright © 2017 by authors and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
对于平面几何里圆锥截线及其聚焦性(聚光性)的观察和研究是经典几何学的重要内容,在很多数学领域乃至物理学上都有重要的应用,一个自然的问题是,在更广泛的内蕴几何空间中,比如常曲率为−1的双曲平面上,有哪些曲线也像平面几何里的圆锥截线一样具有聚焦的性质呢?
在双曲空间中,圆锥截线的几何分类 [1] 是知道的,那么一个直接的问题是,双曲平面上的圆锥截线是否也有相应的聚焦性呢?
为此,本文从聚焦性出发,通过利用双曲平面的Beltrami-Klein坐标系建立并求解聚焦曲线的微分方程,用统一的方法解决了这一问题,证明了双曲平面上非蜕化的圆锥截线也有相应的聚焦性。
并且,有趣的是,由此还发现了一些非圆锥截线的聚焦曲线。
2. 双曲平面的Beltrami-Klein坐标系和点的几何不变性
在区域 之中定义Cayley-Klein-Hilbert度量形式为
之中定义Cayley-Klein-Hilbert度量形式为

其中

定理2.1上述定义的 是双曲空间
是双曲空间 。
。
上述定理描述的坐标系便称为带有该度量的双曲空间的一个Beltrami-Klein坐标系 [2] 。
定理2.2在双曲空间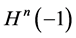 上的Beltrami-Klein坐标系下,双曲空间测地线方程的形态一一对应于欧氏空间中笛卡尔坐标系下落在单位球内部的欧氏直线段的方程的形态 [2] 。
上的Beltrami-Klein坐标系下,双曲空间测地线方程的形态一一对应于欧氏空间中笛卡尔坐标系下落在单位球内部的欧氏直线段的方程的形态 [2] 。
在双曲平面上,Beltrami-Klein坐标系度量矩阵为

若无特别说明,本文中所说的双曲平面都是指Beltrami-Klein坐标系下的Klein圆盘。
3. 圆锥截线的聚焦性
谈及聚焦性(聚光性),必然逃脱不了焦点的几何位置。
定义1双曲平面Beltrami-Klein坐标系在欧氏形态下,其“无穷远不可达边界”即欧氏单位圆将平面分为两个联通的区域,分别称单位圆内的、单位圆上的以及单位圆外的点为双曲平面的有穷远点、无穷远点、超无穷远点。
显见,上述有穷远点、无穷远点、超无穷远点的属性在双曲平面的等距变换下是不变的。
注意,无穷远点、超无穷远点都不是真实的双曲平面上的点。
3.1. 椭圆和双曲线的聚焦性
不是直接去考虑椭圆和双曲线,相反,本文首先考虑拥有类似欧氏椭圆与欧氏双曲线那样聚光性质的曲线,想办法求出其在Beltrami-Klein坐标系下的方程。如果求出了这样的曲线的方程,那么,只需检查椭圆和双曲线是否包含在这种曲线之中;如果包含在内,便完成了椭圆和双曲线聚光性质的证明。反之,则否定了椭圆和双曲线聚光性质的存在。
不失一般性,在双曲平面的Beltrami-Klein坐标系下,取坐标是𝑥轴上欧氏形态对称于坐标原点o的两点 、
、 ,考虑从
,考虑从 点出发的光线(测地线),经过反射后,反射光线所在的测地线经过另一点
点出发的光线(测地线),经过反射后,反射光线所在的测地线经过另一点 的曲线的微分方程,简单的几何分析注意到,这样的曲线有两族,且在反射点处相互垂直。它们的共同几何特征是入射角等于反射角。
的曲线的微分方程,简单的几何分析注意到,这样的曲线有两族,且在反射点处相互垂直。它们的共同几何特征是入射角等于反射角。
定义2称上述两点为该反射曲线的焦点。
设曲线的方程为

则在反射点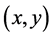 处,曲线的切向量在自然基底下的分量为
处,曲线的切向量在自然基底下的分量为 ,利用定理2.2,入射光线在反射点处具有切向
,利用定理2.2,入射光线在反射点处具有切向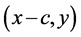 ,反射光线在反射点处具有切向
,反射光线在反射点处具有切向 。由入射角等于反射角,得到两条曲线的统一方程
。由入射角等于反射角,得到两条曲线的统一方程
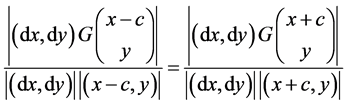 (3.1.1)
(3.1.1)
两边平方整理得

注意到利用关于 的对称性,令
的对称性,令

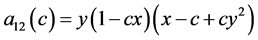
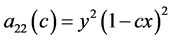

则方程化成

计算得

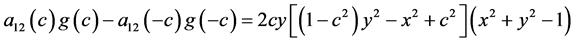
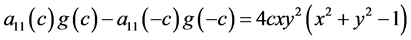
于是方程化为
 (3.1.2)
(3.1.2)
引理1方程(3.1.2)在双曲平面上定义了一个正交标架场。
证明:考虑方程的判别式,当 时,在欧氏单位圆内,有
时,在欧氏单位圆内,有

当 时,方程在欧氏单位圆盘的某一区域上有定义,这个区域是使得下述不等式组成立的欧氏单位圆盘内的区域
时,方程在欧氏单位圆盘的某一区域上有定义,这个区域是使得下述不等式组成立的欧氏单位圆盘内的区域

而由简单的欧氏平面几何知识可知

所表示的区域是两条欧氏直线
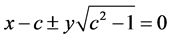
之间包含 轴的部分。而这两条欧氏直线恰好是相交于
轴的部分。而这两条欧氏直线恰好是相交于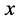 轴上的欧氏单位圆的两条切线。
轴上的欧氏单位圆的两条切线。
同理讨论可得
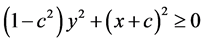
这便说明了对于任意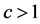 ,在
,在 的条件下
的条件下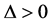 恒成立。即不等式组在整个欧氏单位圆盘上是成立的。证毕。
恒成立。即不等式组在整个欧氏单位圆盘上是成立的。证毕。
推论1当 时,不等式
时,不等式

关于 恒成立。
恒成立。
接下来,对微分方程进行求解。
首先观察,当 ,则微分方程具有简单的形式
,则微分方程具有简单的形式
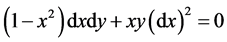
此时方程的两个解为
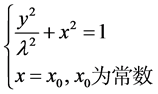
其中第一个解恰好是到𝑥轴的等距线 [1] 的方程。于是有
定理3.1双曲平面的Beltrami-Klein坐标系下,其上的等距线族和测地线族

相互正交,二者共用一对对称无穷远点为焦点 。等距线实聚焦,测地线虚聚焦。
。等距线实聚焦,测地线虚聚焦。
接下来,考察当 时的情形。
时的情形。
若 ,方程的解为
,方程的解为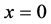 。若
。若 ,方程的解为
,方程的解为 。
。
若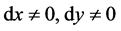 ,根据引理1,由常微分方程理论知,方程(3.1.2)的两个解总是存在的,注意到微分方程的齐次性,假设其积分曲线方程形如
,根据引理1,由常微分方程理论知,方程(3.1.2)的两个解总是存在的,注意到微分方程的齐次性,假设其积分曲线方程形如
 (3.1.3)
(3.1.3)
则
 (3.1.4)
(3.1.4)
联立(3.1.2)、(3.1.3)和(3.1.4)有
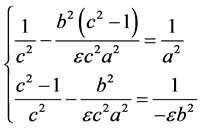
简单的计算知上式是可以求出确定解的,且有
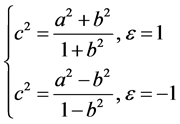
由此便知微分方程的解为
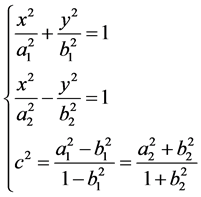 (3.1.5)
(3.1.5)
考虑椭圆 [3] [4] 和双曲线 [5] ,比较其方程系数与焦点的关系式,与上式相符,知二者为微分方程(3.1.2)的解,这便证明了椭圆和双曲线具有聚焦性。
定理3.2双曲平面上的椭圆和双曲线具有焦点聚光性。
从以上的证明中,还可以得到下面一个推论
推论2双曲平面上,同焦点的椭圆和双曲线相互正交。
其实,从椭圆和双曲线分别具有聚光性,那么当二者同焦点时,自然就可推出它们是彼此正交的。这个性质不因为高斯曲率而发生变化;当然在欧氏平面上,同焦点的椭圆和双曲线也彼此正交。不过,假如在未证明椭圆和双曲线的聚光性的条件下,直接验证的办法也可以证明这一点,在此略去。
特别需要说明的是,本文所获方程(3.1.2)的解(3.1.5)的系数特征关系式中,参数 的取值只要求
的取值只要求 。也就是说,本文不仅证明了椭圆和双曲线的聚焦性,还找到了别种聚焦的曲线。
。也就是说,本文不仅证明了椭圆和双曲线的聚焦性,还找到了别种聚焦的曲线。
简单的计算表明,下述方程组

所表示两族曲线也是彼此正交的,它们的两个焦点都是超无穷远点,并且直接分析知道,每一族曲线都有两条对称轴欧氏形态超无穷远延伸上的焦点。
3.2. 测地圆和极限圆的一点聚焦性
从测地圆的定义出发,直接便得到测地圆的聚光性性质。
定理3.3 [高斯引理]测地圆垂直于测地半径。
对于Beltrami-Klein坐标系下的双曲平面来说,有意思的是,垂直于某一条未定曲线的测地线族欧氏形态若相交于一点,那么这条未定曲线的方程也是可以确定的。
定义3称上述测地线族欧氏形态的交点为这条未定曲线的焦点。
不失一般性,考虑从点 (注意没有限定在欧氏单位圆内)出发的光线,设与之垂直的曲线方程为
(注意没有限定在欧氏单位圆内)出发的光线,设与之垂直的曲线方程为

切向在自然基底下的分量为 ,则由与从
,则由与从 点出发的测地线的正交性,其满足的微分方程为
点出发的测地线的正交性,其满足的微分方程为
 (3.2.1)
(3.2.1)
展开有
 (3.2.2)
(3.2.2)
注意到 都不可能为0,有
都不可能为0,有

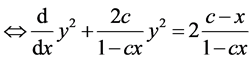
解得
 (3.2.3)
(3.2.3)
另外,当 时,方程(3.2.2)变为
时,方程(3.2.2)变为

积分得
 (3.2.4)
(3.2.4)
这正好是双曲平面上Beltrami-Klein坐标系下测地圆的标准方程。
利用等距变换,容易看出,当 或者
或者 时,微分方程的解表示的曲线是双曲平面的测地圆。
时,微分方程的解表示的曲线是双曲平面的测地圆。
令 ,则由(3.2.3)式有
,则由(3.2.3)式有
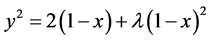
将其整理成下面形式
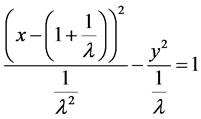 (3.2.5)
(3.2.5)
它所表示的曲线要落在欧氏单位圆盘上,要求曲线与 轴的一个交点落在欧氏单位圆内,有
轴的一个交点落在欧氏单位圆内,有

得
 (3.2.6)
(3.2.6)
由此(3.2.5)式所表示的是欧氏平面上的欧氏椭圆
考虑平移
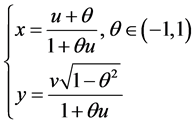 (3.2.7)
(3.2.7)
在此平移之下,方程(3.2.5)化为
 (3.2.8)
(3.2.8)
令

即

则方程(3.2.5)在平移(3.2.7)后有如下一致形式

这正好是极限圆 [1] 的标准方程。
定理3.4极限圆的焦点落在它的无穷远处。
同理可以讨论 时的情形。
时的情形。
3.3. 抛物线的聚焦性
在这一节,本文将首先证明抛物线具有类似于欧氏平面上抛物线那样的聚光性,然后给出一类新的曲线的定义——极限抛物线。
如同前面讨论椭圆和双曲线的聚光性一样,首先考虑拥有像欧氏平面上抛物线那样的聚光性质的曲线,通过建立微分方程,求出其解。然后考虑抛物线,检查其是否落在这样的曲线类之中。
不失一般性,考虑从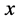 轴上一点
轴上一点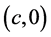 (没有限制在欧氏单位圆内)出发的光线,反射光线沿着方程为
(没有限制在欧氏单位圆内)出发的光线,反射光线沿着方程为 的测地线,简单的几何分析注意到,这样的反射曲线应当有两族,并且,二者在相交处相互垂直,共同的几何特征是反射角等于入射角。
的测地线,简单的几何分析注意到,这样的反射曲线应当有两族,并且,二者在相交处相互垂直,共同的几何特征是反射角等于入射角。
定义4称该点为该反射曲线的焦点。
设曲线的方程为

则在反射点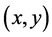 处,曲线的切向量在自然基底下的分量为
处,曲线的切向量在自然基底下的分量为 ,利用定理2.2,入射光线在反射点处的切向为
,利用定理2.2,入射光线在反射点处的切向为 ,反射光线在反射点处的切向为
,反射光线在反射点处的切向为 ,由入射角等于反射角,得到两条曲线的统一方程
,由入射角等于反射角,得到两条曲线的统一方程
 (3.3.1)
(3.3.1)
两边平方展开有
 (3.3.2)
(3.3.2)
展开得
 (3.3.3)
(3.3.3)
计算三项系数分别为



代入(3.3.3)得
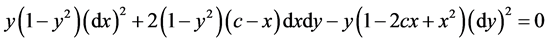 (3.3.4)
(3.3.4)
方程的判别式为

由推论1知,对于任意的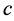 ,方程(3.3.4)在欧氏单位圆内定义了一个正交的标架场。
,方程(3.3.4)在欧氏单位圆内定义了一个正交的标架场。
当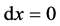 时,方程的解为
时,方程的解为
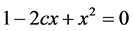
即

其中

当 时,方程的解为
时,方程的解为 (
( 舍去)。
舍去)。
除此以外,根据前面的经验,设方程的解是
 (3.3.5)
(3.3.5)
其中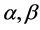 为待定系数。则
为待定系数。则
 (3.3.6)
(3.3.6)
联立(3.3.4) (3.3.5) (3.3.6)有
 (3.3.7)
(3.3.7)
故知方程(3.3.4)的两个解为
 (3.3.8)
(3.3.8)
需要注意的一点是,这两个解中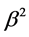 可以将平方去掉,并不影响最终的解。也就是说,
可以将平方去掉,并不影响最终的解。也就是说, 这个参数作为一个整体参数,可以为正也可以为负,只要不是0就可以了。
这个参数作为一个整体参数,可以为正也可以为负,只要不是0就可以了。
另外一点需要提出的是,注意到解曲线(3.3.8)中,当 时,对于任意的参数
时,对于任意的参数 ,得到一个“公共的解”
,得到一个“公共的解”

这正好是欧氏单位圆。为了解曲线的意义有效性,特别需要说明解方程的参数中,需 。此时,可以看到刚好可以由参数确定出焦点横坐标
。此时,可以看到刚好可以由参数确定出焦点横坐标 。
。
定理3.5抛物线具有焦点聚焦性,反射光线与准线正交。
证明:考虑抛物线 [1] 焦点与方程系数的关系,有

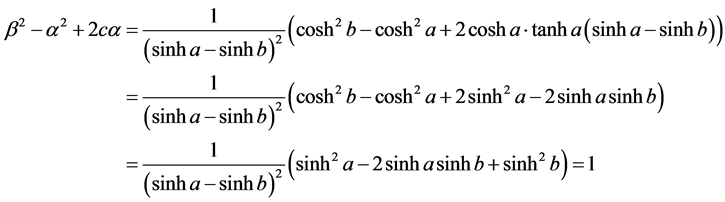
满足方程(3.3.8)的第二式。这说明抛物线具有焦点的聚焦性。
关于定理的后半句,定理3.1保证了这一点。证毕。
推论3方程组(3.3.8)表示的两族抛物线
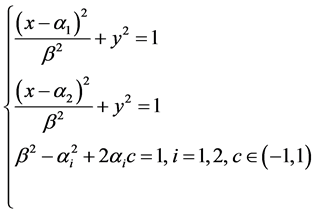
相互正交,共用焦点 。
。
这个推论只需验证两族抛物线确实相交于欧氏单位圆盘内即可,计算是直接的,略去。
同样,取 ,由(3.3.8)得
,由(3.3.8)得
 (3.3.9)
(3.3.9)
考虑在平移(3.2.7)下该方程所表示曲线的运动变化,当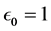 时得
时得
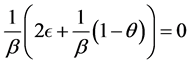 (3.3.10)
(3.3.10)
 (3.3.11)
(3.3.11)
 时得
时得
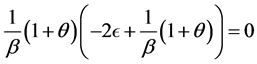 (3.3.12)
(3.3.12)
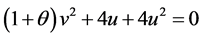 (3.3.13)
(3.3.13)
注意方程(3.3.11)、(3.3.13)在形式上与极限椭圆 [1] 和极限双曲线 [1] 的标准方程形式上是类似的:
 (3.3.14)
(3.3.14)
由于 ,则
,则 ,因此如果(3.3.14)是(3.3.9)所表示的曲线平移得到的,那么必须有
,因此如果(3.3.14)是(3.3.9)所表示的曲线平移得到的,那么必须有
 (3.3.15)
(3.3.15)
比较极限椭圆的标准方程,对于极限椭圆,参数范围是
由此便得:在(3.3.15)的条件下,方程(3.3.14)与焦点在无穷远处的“假抛物线”平移一一对应。
定义5在双曲平面的Beltrami-Klein坐标系下,称标准方程

所表示的曲线为极限抛物线。
也即是说,极限抛物线可以看成是焦点在无穷远处的“假抛物线”。
3.4. 极限曲线的聚焦性
所谓极限曲线,就是指极限圆 [1] 、极限抛物线、极限双曲线 [1] 和极限椭圆 [1] 。四者可包含为一个标准方程

如同证明椭圆和双曲线的聚光性时的那样,将那里考虑 轴上的任意欧氏形态对称于坐标原点的两点改为任意两点
轴上的任意欧氏形态对称于坐标原点的两点改为任意两点 ,经过类似计算得到从点
,经过类似计算得到从点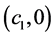 出发的测地线被反射后经过另一点
出发的测地线被反射后经过另一点 的反射曲线的统一微分方程为
的反射曲线的统一微分方程为
 (3.4.1)
(3.4.1)
其中
 (3.4.2)
(3.4.2)
定义6称上述两点为该反射曲线的焦点。
当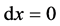 时,方程的解为
时,方程的解为

该解有意义的情况下确定的解曲线是测地线。
当 时,方程的解为
时,方程的解为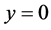 。
。
除此以外,假设方程的解为
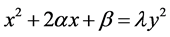 (3.4.3)
(3.4.3)
其中 为待定系数,则
为待定系数,则

代入(3.4.1)中得

注意到(3.4.3)式,代入上式得

展开有

合并同类项得
 (3.4.4)
(3.4.4)
注意到,此式应当与(3.4.3)式保持一致。故
 (3.4.5)
(3.4.5)
消去 ,得
,得
 (3.4.6)
(3.4.6)
故可得方程(3.4.1)的解曲线方程为
 (3.4.7)
(3.4.7)
不妨取

由(3.4.6)式得

取

则(3.4.7)式即为
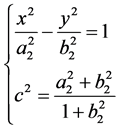
可以看到,这正好是双曲线。对于椭圆和等距线,也可以如是验证它们的一致性。
现在,可以考虑极限曲线的聚焦性了。对应于方程(3.4.3)的系数,有

代入(3.4.6)有

由此根据(3.4.2)得

即为聚焦点的横坐标。
定理3.6双曲平面的Beltrami-Klein坐标系下,标准方程

所表示曲线的两个焦点坐标分别为 、
、 。
。
取 ,分别考察极限椭圆和极限双曲线的焦点坐标,二者共有一个焦点
,分别考察极限椭圆和极限双曲线的焦点坐标,二者共有一个焦点 ,极限椭圆的另一个焦点坐标为
,极限椭圆的另一个焦点坐标为

该焦点属于区间 ;极限双曲线的另一个焦点坐标为
;极限双曲线的另一个焦点坐标为
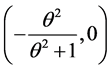
该焦点属于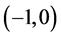
由此可见,标准方程表示的极限椭圆和极限双曲线是不会相互正交的,因为它们不可能共用焦点。但是,极限椭圆和极限双曲线都是一个焦点无穷远,而另一个焦点有穷远的曲线,这也就意味着,共用一对焦点的极限椭圆和极限双曲线是正交的,只不过是它们此时的方程不会同是标准的罢了。
当 时,定理描述的是极限圆。与已有的结果一致,极限圆的焦点重合为无穷远
时,定理描述的是极限圆。与已有的结果一致,极限圆的焦点重合为无穷远
点。
当 时,定理描述的是极限抛物线。其一个焦点是无穷远点,另一个焦点的坐标
时,定理描述的是极限抛物线。其一个焦点是无穷远点,另一个焦点的坐标
为

该焦点落在区间 之外。由此亦可见极限抛物线与前三者之不同。
之外。由此亦可见极限抛物线与前三者之不同。
推论4极限圆两个焦点重合在无穷远处;极限椭圆和极限双曲线两个焦点有一个在无穷远处,有一个在有穷远处;极限抛物线两个焦点,有一个在无穷远处,有一个在超无穷远处。
从这个推论,极限抛物线似乎有两种聚焦性,在这里它有两个焦点,一个在无穷远处,一个在超无穷远处;而根据极限抛物线的定义,它则是一个焦点在无穷远处的“假抛物线”,这是不是矛盾了呢?事实上是不矛盾的,因为双曲平面上测地线的欧氏形态只要不相交于欧氏单位圆上及其内部,就可以看成是“聚焦于超无穷远点”。
至此,本文解决了双曲平面上非蜕化圆锥截线的聚焦性问题。
需要提及的是,蜕化的圆锥截线测地线是有一对无穷远焦点的虚聚焦曲线。
另一方面,通过前文的叙述可以看到,等距线、极限圆和极限抛物线不是圆锥截线,但它们也有聚焦性。同时,下述方程组

所表示的曲线,同样也不是圆锥截线,但它也有聚焦性。
这说明,在双曲平面上,非蜕化的圆锥截线具有聚焦性质,但是具有聚焦性质的曲线却不仅仅是圆锥截线。这与欧氏平面几何的内容是不同的。
致 谢
感谢国家自然科学基金的资助!
资助信息
受国家自然科学基金(11171025) (11471039)资助。
文章引用
何 海,王幼宁. 双曲平面上非蜕化圆锥截线的聚焦性
The Focus Properties of Nonsingular Conic Curves in Hyperbolic Plane[J]. 理论数学, 2017, 07(04): 334-348. http://dx.doi.org/10.12677/PM.2017.74043
参考文献 (References)
- 1. 王幼宁. 双曲空间型中圆锥截线的度量几何分类[J]. 理论数学, 2012, 2(2): 97-102.
- 2. 王幼宁, 李德龙. 双曲空间中的Beltrami-Klein坐标系[J]. 北京师范大学学报(自然科学版), 2010, 46(1): 13-16.
- 3. 王幼宁, 吴英丽. 关于双曲空间的椭圆[J]. 北京师范大学学报(自然科学版), 2007, 43(1): 6-9.
- 4. 王幼宁, 吴英丽. 双曲平面上椭圆的凸性和运动[J]. 北京师范大学学报(自然科学版), 2008, 44(5): 469-471.
- 5. 王幼宁, 连詠欣. 关于双曲平面上的双曲线[J]. 北京师范大学学报(自然科学报), 2011, 47(2): 115-121.