Pure Mathematics
Vol.
10
No.
04
(
2020
), Article ID:
35310
,
13
pages
10.12677/PM.2020.104048
Relation and Lagrange-Point Conjecture of 2 Spherical Centers of 8 Intersection Points between Euler-Line and Orthogonal 4 Spheres
—Application of Pythagorean Theorem of Four-Dimensional Volume (Formula 8)
Guowei Cai
Shanghai Huimei property Co., Ltd., Shanghai

Received: Apr. 1st, 2020; accepted: Apr. 21st, 2020; published: Apr. 28th, 2020

ABSTRACT
It is proved that the four points of orthogonal 4-sphere, concave and convex, have their own concentricity and radii, and the three coordinates of their respective concentric coordinates are all the same. It is proved that with the change of the same dimension, the points of the 2 spherical centers and the Euler-line have the difference of common point, collinear, coplanar and common body. The figure shows that the Euler-line meets the line of 2 spherical centers approximately at the H point. According to the connection of 4 soap bubbles, the conjecture of 5 Lagrange-points is proposed.
Keywords:Volume Pythagorean Theorem, Orthogonal 4 Spheres, Eight Intersections of Sphere, Lagrange Point, Proof, Algorithm

正交4球面8交点2共球心与欧拉线关系 及Ln猜想
——四维体积勾股定理的应用(公式八)
蔡国伟
上海汇美房产有限公司,上海

收稿日期:2020年4月1日;录用日期:2020年4月21日;发布日期:2020年4月28日

摘 要
证明正交4球,球面内凹、外凸各4点有各自的共球心及半径,其各自球心坐标的3个分坐标代数值都相同,并得出2球心间距公式;且证明随相同维数的变化,2球心与欧拉线各点具有共点、共线、共面、共体的区别。图示欧拉线与2球心连线约交于H垂心点;根据4个肥皂泡相接,提出5个拉格朗日点的猜想。
关键词 :体积勾股定理,正交4球,球面8交点,拉格朗日点,证明,算法

Copyright © 2020 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution-NonCommercial International License (CC BY-NC 4.0).
http://creativecommons.org/licenses/by-nc/4.0/


1. 引言
正交4球 [1] 8球面交点 [2] 为8原点,其中各4点内凹、外凸的2共球半径及其球心坐标的性质有哪些特征?以及2球心连线与欧拉线 [3] 的关系如何?自然界中可见哪些现象?
2. 证明正交4球球面内凹和外凸各4交点共球半径及其坐标
2.1. 设共球半径及其球心坐标符号
2.1.1. 正交4球球面内凹4交点坐标见文 [2],其共球半径及球心符号为
设4个球面内凹交点
坐标见文 [2],共球半径平方为
,共球球心为
。
2.1.2. 正交4球球面外凸4交点坐标见文 [2],其共球半径及球心符号为
设4个球面外凸交点
坐标见文 [2],共球半径平方为
,共球球心为
。
2.2. 计算证明正交4球球面内凹、外凸各4点2个共球半径及其球心坐标
根据文 [2] 得知,正交4球的球面构成内凹、外凸各4点3球面交点为8原点,其中可分内凹4点和外凸4点2组。计算证明2组各4原点共球和球心坐标如下:
2.2.1. 计算证明正交4球球面内凹4交点的共球半径及其球心坐标
证明正交4球面4内凹交点共球球心有相同的3个分坐标,且均为共球半径的
,即共球半径为各相同分坐标的
倍。即证明:
正交4球面4内凹交点共球半径为:
(1)
3个分坐标相同的共球球心坐标为:
(2)
证明如下:
• 根据2点距离公式,球面内凹4原点A−,B−,C−,D−,与其共球球心O−可联立方程组为:
这里:
, ;
• 用高斯消元法求得内凹4点共球心
坐标为:
(注:上述3个分坐标代数值均相同)
• 将上述坐标代入联立公式任何一行,得内凹4点共球半径为:
公式(1)、公式(2)证毕。
2.2.2. 计算证明正交4球球面外凸4交点的共球半径及其球心坐标
证明正交4球面4外凸交点共球球心有相同的3个分坐标,且均为共球半径的
,其共球半径为各相同分坐标的
倍,且与内凹共球半径共轭,区别在分母正的体积元为负。即证明:
正交4球面4外凸交点共球半径为:
(3)
3个分坐标相同的共球球心坐标为:
(4)
证明如下:
• 根据2点距离公式,球面外凸4原点A+,B+,C+,D+与其共球球心O+可联立方程组为:
这里:
, ;
• 用高斯消元法求得外凸4点共球心
坐标为:
(注:上述3个分坐标代数值均相同)
• 将上述坐标代入联立公式任何一行,得外凸4点共球半径为:
公式(3)、公式(4)证毕。
2.2.3. 计算证明正交4球球面内凹、外凸共球球心间距
证明正交4球面内凹、外凸交点2共球球心间距为:
(5)
• 根据2点距离公式,因内凹、外凸2共球球心坐标均分别相同,其距离公式
• 两边开方为:
公式(5)验证毕。
2.3. 证明正交4球球面内凹、外凸2共球心与欧拉线关系
2.3.1. 证明当4维相同,5点共点
当正交4球半径均相同时,内凹、外凸球面交点2共球球心
与
欧拉线(欧拉线权取3点坐标见文 [3],其余点作省略) 5点均共点。其坐标为位置:见图1。
(6)
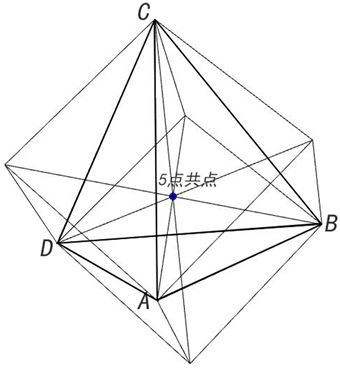
Figure 1. 4-Dimensional same, 5-point common point graph
图1. 四维相同,5点共点图
公式(1)坐标共点验证如下:
当
时:
;
• 验算垂心H坐标:
• 验算重心G坐标:
• 验算外接球球心O坐标:
• 验算内凹球面交点共球心
坐标:
• 验算外凸球面交点共球心
坐标:
公式(6)验证毕。
2.3.2. 当3维相同,5点共垂线
当3维相同:正交4球球面内凹、外凸2共球球心
连线与
欧拉线各点,5点共垂线(且该垂线过另一点球心)。见图2。
根据文 [2] 得知:垂线过球心
,也过原点
,根据2点式过D点垂线的直线坐标参数方程为:
这里:
,。
当
时:根据2点式过D垂线的直线坐标参数方程为:
即:
(7)
这里:
,, 以下同。
可见当3维相同时,该线每点的3个分坐标均相同,点的变化仅在于参数
。
图2. 三维相同6点共线图
验证如下:
当
时
• 验算垂心H坐标为:
解方程得参数:
。
• 验算重心G坐标为:
解方程得参数:
。
• 验算外接球球心O坐标为:
解方程得参数:
。
• 验算内凹球面交点共球心
坐标为:
解方程得参数:
。
• 验算外凸球面交点共球心
坐标为:
解方程得参数:
。
• 验算正交球球心D坐标为:
解方程得参数:
。
公式(7)证毕。
同理:当其余3组ABD,ACD,BCD半径相同时,上述5点坐标,且依次共线过球心C、B、A垂线(略)。
2.3.3. 当2维相同,5点共垂面
当2维相同:正交4球球面内凹、外凸2共球球心
线与
欧拉线交于H,5点共垂直面。且该面垂直交同维长2球心连线中点、且过另2点球心间连线。见图3。
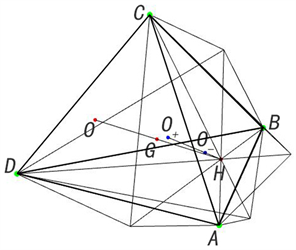
Figure 3. 2-Dimensional same, 7-point coplanar (The above is the diagram of 2 observation points)
图3. 二维相同,7点共面图(上述为2个视点图)
例:
• 证明当
2维相同,
7点中任意取C,D,H 3点的平面方程见文 [4] 为:
(8)
当
2维相同,欧拉线各点H,G,O与球面内凹、外凸2共球球心
连线约交于垂心H,上述5点共面,该共面垂直交于A,B 2球心连线中点,且与C、D 2球心连线共面。其平面方程
见文 [4]:见图3。
当
时:
,
(这里取
)
将上述
7点中任意3点的
平面方程均为:
公式(8)证毕。
同理可证:(平面方程参见文 [4])
当
则
7点共面于
平面,该平面⊥交于AC连线中点,平面方程为:
;
当
则
7点共面于
平面,该平面⊥交于BC连线中点,平面方程为:
;
当
则
7点共面于
平面,该平面⊥交于AD连线中点,平面方程为:
;
当
则
7点共面于
平面,该平面⊥交于BD连线中点,平面方程为:
;
当
则
7点共面于
平面,该平面⊥交于CD连线中点,平面方程为:
;
• 共面的欧拉线
与
连线约交于H点,计算证明交点不在H点:
根据
2点式直线参数方程:
(9)
根据
2点式直线参数方程:
(10)
将公式(9)、(10)联立将垂心坐标代入:
(11)
由于
2点坐标的x,y,z分坐标均各自相同,而H仅x,y 2分坐标相同 z坐标则不同,因此计算出上述2线仅约交于H点。
不妨将图3的代数值
计算证明
3点的间距为:
因此:虽然共面不平行的2线有交点,目测约交点在H点。其间距和夹角的精确数值仍然需由点坐标得出。
2.3.4. 当4维均不同,5点共体
当四维均不同时,正交4球球面内凹、外凸2共球球心
线与
欧拉线交于H,5点共体(该体包含:4个正交球的综合体)。其2线交点同样无法用公式证明,仅作3D图目测可见约交于H点。
例:当
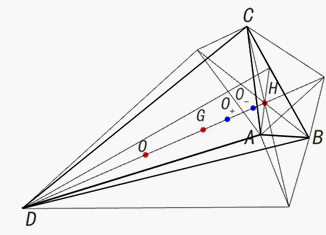
,作图后可见欧拉线与凹凸球面共球球心2点连线约交于垂心。见图4
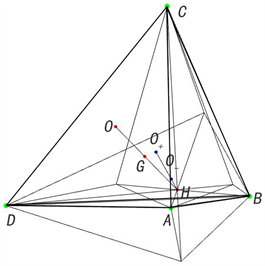
Figure 4. 4-D is not the same, 5-point 2-line approximately intersects H-point
图4. 四维不相同,5点2线约交于H点图
3. 总结
3.1. 正交4球球面内凹、外凸交点2共球球心
2点的性质
• 2点共球球心,各自的分坐标均相同;
• 点在H点附近;
点在G点附近,
与
2点间距等于
;
• 2个共球半径共轭于分母的体积元。
3.2.
与欧拉线关系
• 当正交4球半径相同时,
与
2点与欧拉线各点共垂心点;
• 当正交4球其中3球半径相同时,
与
2点与欧拉线各点共垂线;
• 当正交4球其中2球半径相同时,
与
2点与欧拉线各点共垂面于相同2球心间中点;2球心连线与欧拉线约交于H;
• 当正交4球半径均不相同时,
与
2点与欧拉线共体;2球心连线与欧拉线约交于垂心H。
3.3. 拉格朗日5点的猜想
• 自然界中任意4个相接的肥皂泡均与正交4球是等价的,因此认为引力与泡沫的张力是等价的。引力很难直观,而泡沫张力能方便观察。
• 通过观察泡沫张力:可见正交4球球面外凸4交点和垂心共5点,当在水平面(相当于地球球面)与3个相接的肥皂泡等价于4球正交,上述5点中除了1点在3肥皂泡球面交点外的其余4点均在水平面上。而球面内凹4点与外凸4点正好反差180度,张力相互抵消后内凹4点消失,仅见垂心H。因此猜想上述5点:为正交4个天体间L1~L5拉格朗日点 [5]。
文章引用
蔡国伟. 正交4球面8交点2共球心与欧拉线关系及Ln猜想——四维体积勾股定理的应用(公式八)
Relation and Lagrange-Point Conjecture of 2 Spherical Centers of 8 Intersection Points between Euler-Line and Orthogonal 4 Spheres—Application of Pythagorean Theorem of Four-Dimensional Volume (Formula 8)[J]. 理论数学, 2020, 10(04): 379-391. https://doi.org/10.12677/PM.2020.104048
参考文献
- 1. 蔡国伟. 体积勾股定理的证明[J]. 理论数学, 2019, 9(6): 723-729.
- 2. 蔡国伟. 证明正交四球心间15个垂心球及距离公式的算法[J]. 理论数学, 2019, 9(8): 928-948.
- 3. 蔡国伟. 证明以正交4球半径为4元数欧拉线的算法[J]. 理论数学, 2019, 9(9): 1043-1059.
- 4. 蔡国伟. 证明正交4球6平面及四维垂直的四维空间算法[J]. 理论数学, 2020, 10(1): 23-29.
- 5. 张恒谦. 奇妙的拉格朗日点[J]. 中学物理教学参考, 2011, 40(10): 29-30.