ABSTRACT

In this paper, because of infinite-dimensional nature and complex nonlinearities of the distributed parameter systems, a new data-driven modeling method has been proposed. The spatiotemporal output of the system is measured at a finite number of spatial locations; at the same time it is assumed that the input of the system is a temporal variable. Firstly, Karhunen-Loève (K-L) decomposition is used for dimension reduction to get PCA eigenvectors, which can be utilized to extract the nonlinear basis functions in dominant space. After using time-space separation to get the temporal coefficients, then combining the temporal coefficients and the excitation input signal as input and output information, the NARX model can be identified by using Elman neural network whose structure parameters have been optimized by FOA. Finally, model has been reconstructed and the predicted output gotten. Simulation result shows that the proposed modeling method can achieve good performance for distributed parameter systems.

Keywords:Distributed Parameter System, Time/Space Separation, FOA Algorithm, Elman Neural Network, NARX Model

基于时空FOA-Elman的分布参数系统建模

——时空建模

杨仁建，范瑛琦

中国石化石油化工科学研究院，北京

收稿日期：2019年1月28日；录用日期：2019年2月6日；发布日期：2019年2月13日

摘 要

本文针对具有无穷维时空特性和复杂非线性特性的分布参数系统，提出了一种基于数据驱动的建模方法。系统的时空输出可以由分布在空间中的有限个传感器获得，同时假设系统输入为有限维时间变量。首先利用Karhunen-Loève (K-L)分解对系统进行模型降维，得到主元特征向量，之后提取得到系统的一组主导空间基函数，利用时空分解获得系统时间系数，随后结合时间系数与系统激励构成输入输出信息，利用FOA算法优化Elman神经网络结构参数，后用优化的Elman神经网络辨识出系统时域NARX模型，最后进行模型重构，得到预测输出。仿真表明，上述建模方法能够对分布参数系统取得良好的建模效果。

关键词 :分布参数系统，时空分解，FOA算法，Elman神经网络，NARX模型

Copyright © 2019 by author(s) and Hans Publishers Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY).

http://creativecommons.org/licenses/by/4.0/

1. 引言

广泛存在于生产实践中的物理、化学过程(如：石油炼制、化学制药、工业催化等)都是分布参数系统(distributed parameter system, DPS)。由于其输入输出的非线性时空耦合特性和无穷维特性，基于集中参数系统的传统建模方法无法对此类时空分布系统进行准确建模。虽然偏微分方程(partial differential equations, PDE)能够准确描述分布参数系统的内部机理，但受限于数值计算能力和实际系统中有限的执行机构和检测机构，而很难得到实际应用。因此，有必要对模型进行降维，建立可行的有限维模型。

如果分布参数系统的偏微分方程描述为可知的，则使用传统方法(如：有限差分法和有限元法等)通过离散化将原微分方程转化为差分方程组，但是为了保证模型精度，通常会产生一个高维的常微分方程 [1] (ordinary differential equation, ODE)，这将直接导致模型设计困难同时难以实际应用。在特定条件下，基于正交分解(proper orthogonal decomposition, POD)的Galerkin方法 [2] 、近似惯性流形法 [3] 等加权残差法可以将无穷维的分布参数系统降为有限维系统。然而在实际工业过程中，通常无法直接得到系统的结构和参数，同时还会受到复杂的边界条件和外部干扰的影响，导致无法直接得到系统模型。因此，对于未知的非线性分布参数系统，有必要对输入输出进行观察得到系统的低阶模型。

主元分析方法 [4] - [9] (principal component analysis, PCA)又被称为：K-L分解法，是一种基于数据建模的常用方法，K-L分解可对非线性DPS的时间和空间进行变量分离。通过选取合适的主导空间基函数，利用时空分解获得系统时间系数并结合系统输入信号构成非线性自回归各态经历模型(nonlinear autoregressive exogenous, NARX)模型 [10] 的输入输出信息。

Elman神经网络 [11] 是一种动态递归神经网络，其结构简单，运算量小，非常适合于实时非线性动态系统辨识，因此本文使用Elman神经网络对NARX模型进行估计。然而常规Elman神经网络学习算法存在极易陷入局部最优，收敛速度慢等特点，因而考虑使用一种全局优化算法对Elman神经网络的权值和阀值进行全局优化。果蝇优化算法(Fruit Fly Optimization Algorithm, FOA) [12] [13] 是一种新的全局优化算法，具有收敛速度快，精度高的特点。因此，本文使用FOA-Elman神经网络 [14] 估计NARX模型。

本文将介绍一种基于时空FOA-Elman的分布参数建模方法。本方法主要包含两个过程，首先通过K-L分解对分布参数系统的输出进行时空分解。然后基于所得时间系数和系统激励使用FOA-Elman辨识NARX模型。

2. 问题描述

对于一个非线性分布参数系统，系统输入控制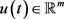为具有特定空间分布的时间输入信号， $y\left(x,t\right)\in ℝ$ 为系统时空输出，其中： $x\in \Omega$ 为空间变量， $\Omega$ 为时空域，为时间变量。由于分布参数系统的无穷维特性，为实现高精度建模，需要无穷多个执行和检测机构，但是受限于技术和成本，在实际应用中仅使用有限个检测和执行机构，其数量取决于过程复杂度和建模要求。本文研究目的为从时间输入 ${\left\{u\left(t\right)\right\}}_{t=1}^L$ 和时空输出 ${\left\{y\left(x_i,t\right)\right\}}_{i=1,t=1}^{N,L}$ 辨识出一个低维时空模型，其中 $t=1,2,\cdots ,L$ 表示在时间上的 $L$ 个离散采样点， $i=1,2,\cdots ,N$ 表示分布在空间上的 $N$ 个检测装置。为此，首先通过K-L分解从系统的时空输出数据中提取表征系统绝大部分能量的空间主导基函数 $\phi \left(x\right)$ ，然后使用snapshots方法，利用空间基函数和系统在各个时刻的输出数据点，获得与空间位置无关的系统时间系数 $y\left(t\right)$ 。最后根据系统输入信号和所得到的时间系数 $y\left(t\right)$ ，利用系统辨识方法，如本文采用的FOA-Elman神经网络等，得到一个与空间位置无关的时域NARX模型。系统结构如图1所示：

图1. 分布参数系统的时空NARX建模

3. 时空分离及FOA-Elman模型辨识

3.1. 时空分离

在所有通过线性展开对时间和空间进行分离的方法中，K-L分解是获取低维模型是最为有效的方法。换言之，即对于给定的建模误差，通过K-L分解得到的基函数个数是最少的。

3.1.1. 时空分离方法

为简化处理过程，假设系统输出 ${\left\{y\left(x_i,t\right)\right\}}_{i=1,t=1}^{N,L}$ 均匀地分布在时间和空间中。假设系统正交空间基函数为 $$ ，时间系数为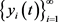：，则系统空间输出可以表示为如下形式：

$y\left(x,t\right)={\displaystyle \underset{i=1}{\overset{\infty }{\sum }}{\phi }_i\left(x\right)y_i\left(t\right)}$ (1)

由于空间基函数的正交特性，即

$\left({\phi }_i\left(x\right),{\phi }_j\left(x\right)\right)={\displaystyle {\int }_{\Omega }{\phi }_i\left(x\right){\phi }_j\left(x\right)\text{d}x}=\{\begin{array}{l}0,i\ne j\\ 1,i=j\end{array}$ (2)

为了求得系统的主导空间基函数，可以转化为求解式(3)所述最小化问题：

$\{\begin{array}{l}\underset{\phi i(x)}{\min }\langle \left[y\left(x,t\right)-{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\phi }_i\left(x\right){\left({\phi }_i\left(x\right),y\left(x,t\right)\right)}^2}\right]\rangle \\ s.t.\left({\phi }_i\left(x\right),{\phi }_i\left(x\right)\right)=1,{\phi }_i\left(x\right)\in L^2\left(\Omega \right),i=1,\cdots ,n\end{array}$ (3)

其中 $\langle f\left(x,t\right)\rangle =\frac{1}{L}{\displaystyle \underset{t=1}{\overset{L}{\sum }}f\left(x,t\right)}$ 为集合均值的定义。该最小化问题对应的拉格朗日函数约束优化问题为：

$J=\langle \left[y\left(x,t\right)-{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\phi }_i\left(x\right){\left({\phi }_i\left(x\right),y\left(x,t\right)\right)}^2}\right]\rangle +{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\lambda }_i\left(\left({\phi }_i,{\phi }_i\right)-1\right)}$ (4)

针对上述的最优化问题，其极值存在的必要条件为：

$\{\begin{array}{l}{\displaystyle {\int }_{\Omega }R\left(x,\zeta \right){\phi }_i\left(\zeta \right)\text{d}\zeta }={\lambda }_i{\phi }_i\left(x\right),\\ s.t.\left({\phi }_i,{\phi }_i\right)=1,i=1,\cdots ,n\end{array}$ (5)

其中 $R\left(x,\zeta \right)=\langle y\left(x,t\right),y\left(\zeta ,t\right)\rangle$ 为空间两点的相关函数。因此，求解式(4)最优化问题转化为求解必要条件式(5)的解。

我们测得的数据总是离散地分布在空间中，因此必须使用数值法求解式(5)。通过离散化积分方程，式(5)转化为 $N\times N$ 矩阵的特征值问题，这样可以在 $N$ 个空间采样点上获得 $N$ 个特征值。对于无法获取样本点的地方可以采用插值法获得。

3.1.2. 快照(Snapshots)法

当时间节点数 $L$ 小于空间节点数 $$ 时，使用“snapshots” [15] 方法可以快速有效求得式(5)的解。假设空间基函数 ${\phi }_i\left(x\right)$ 是snapshots的线性组合：

${\phi }_i\left(x\right)={\displaystyle \underset{t=1}{\overset{L}{\sum }}{\gamma }_{it}y}\left(x,t\right)$ (6)

将式(6)带入式(5)，可得：

${\displaystyle {\int }_{\Omega }\frac{1}{L}{\displaystyle \underset{t=1}{\overset{L}{\sum }}y\left(x,t\right)y\left(\zeta ,t\right)}{\displaystyle \underset{k=1}{\overset{L}{\sum }}{\gamma }_{ik}y\left(\zeta ,k\right)\text{d}\zeta }}={\lambda }_i{\displaystyle \underset{t=1}{\overset{L}{\sum }}{\gamma }_{it}y\left(x,t\right)}$ (7)

定义空间两点相关函数为：

$C_{tk}=\frac{1}{L}{\displaystyle {\int }_{\Omega }y\left(\zeta ,t\right)y\left(\zeta ,k\right)\text{d}\zeta }$ (8)

因此，式(5)的 $N\times N$ 矩阵特征值问题转化为如下 $L\times L$ 矩阵的特征值求解问题：

$C{\gamma }_i={\lambda }_i{\gamma }_i$ (9)

其中 $$ 为第 $i$ 个特征向量。分别将特征向量 ${\gamma }_1,\cdots ,{\gamma }_L$ 带入式(6)即可求得对应的空间基函数 ${\phi }_1\left(x\right),\cdots ,{\phi }_L\left(x\right)$ 。因为矩阵 $$ 为对称半正定，因此由式(9)所得的特征向量所对应的空间基函数 ${\phi }_1\left(x\right),\cdots ,{\phi }_L\left(x\right)$ 为正交的，后对其进行标准化处理即可获得空间基函数 ${\phi }_1\left(x\right),\cdots ,{\phi }_L\left(x\right)$ 。

当求得空间基函数，就可以使用式(10)求得相应的时间系数：

$y_i\left(t\right)=\left({\phi }_i\left(x\right),y\left(x,t\right)\right),i=1,\cdots ,n$ (10)

在建模中，系统空间输出一般由反映系统主要能量的前 $n$ 个主导空间基函数构成，即：

$y_n\left(x,t\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\phi }_i\left(x\right)y_i\left(t\right)}$ (11)

3.1.3. 维数n的选取

对于建模选取的主导空间基函数个数 $n$ 而言，其个数越多，所能反映的系统能量就越多，但会增加系统建模的复杂度 [13]。定义系统全部能量为所有特征值之和，则最大特征值对应的空间基函数所反映的系统能量是最多的。对于每个空间基函数，基于其特征值，所占系统能量为：

$E_i=\frac{{\lambda }_i}{{\displaystyle \underset{j=1}{\overset{L}{\sum }}{\lambda }_j}}$ (12)

一般来说，当前 $n$ 个空间基函数所占系统总能量的百分比大于99.9或99.99时，则认为该组空间基函数可以反映出系统绝大部分能量。下文中将通过仿真实例来说明，只要选取合适的空间基函数个数 $n$ ，模型就可以达到要求的精度 [16]。

3.2. FOA-Elman模型辨识

假设 $u\left(t\right)$ 和 $y\left(t\right)$ 可以由NARX模型描述：

$y\left(t\right)=F\left[y\left(t-1\right),\cdots ,y\left(t-n_y\right),u\left(t-1\right),\cdots ,u\left(t-n_u\right)\right]$ (13)

其中， $u\left(t\right)\in {\Re }^m$ 和 $y\left(t\right)\in {\Re }^n$ 分别表示时间输入和输出， $n_u$ 和 $n_y$ 分别表示最大输入和输出滞后。

NARX模型为黑箱模型，建模过程无需知道其内部机理，可以利用输入、输出数据建立数学模型。由于神经网络具有强大的非线性逼近能力、快速并行运算能力、较强的容错性和鲁棒性等特点，因而在非线性系统辨识领域有着广泛的应用。其中Elman神经网络是一种典型的动态神经网络，能够直接反映系统的动态特性，广泛应用于动态系统建模中，然而常规Elman神经网络学习算法存在极易陷入局部最优，收敛速度慢等特点，一种新的全局优化算法——FOA算法，可对Elman神经网络的权值和阀值进行全局优化。在本文中，我们将利用基于FOA的Elman神经网络对NARX模型进行辨识。

3.2.1. Elman神经网络

Elman神经网络由四层网络组成：输入层、隐含层(中间层)、承接层和输出层。Elman神经网络是在前馈神经网络的隐含层中增加一个承接层，隐含层的输出通过承接层连接到隐含层的输入。承接层作为一步时移算子使网络具有记忆功能，增强了系统对历史数据的敏感性，进而使模型具有动态处理数据的能力，能直接反映动态过程的系统特性。

Elman神经网络的非线性状态空间表达式如下：

$y\left(k\right)=g\left(w^{3}x\left(k\right)\right)$ (14)

$x\left(k\right)=f\left(w^1{x}_c\left(k\right)\right)+w^2\left(u\left(k－1\right)\right)$ (15)

$x_c\left(k\right)=x\left(k-1\right)$ (16)

式中 $u$ 为输入向量； $x$ 为隐含层节点输出向量， $y$ 为输出节点向量， $x_c$ 为状态反馈向量。 $w^1$ 为承接层到隐含层的连接权值； $w^2$ 为输入层到隐含层连接权值； $w^3$ 为隐含层到输出层连接权值。 $g(*)$ 为输出神经元的传递函数，是隐含层输出的线性组合； $f(*)$ 为隐含层神经元的传递函数，常采用 $S$ 函数。

3.2.2. 果蝇优化算法

果蝇优化算法是由台湾学者潘文超博士通过对果蝇觅食过程的模拟，提出的一种全新的寻找函数全局最优解的迭代智能优化算法。果蝇凭借着敏锐的嗅觉器官可以分辨数十公里外的各种气味，然后向该位置飞去，也可以利用视觉器官飞向食物和其它果蝇。按照果蝇寻找食物的过程，可以将FOA算法总结为以下步骤：

Step 1：设定群体规模，最大迭代次数，随机初始化果蝇群体位置 $X\_axis$ ， $Y\_axis$ 。

Step 2：随机果蝇个体搜索方向和搜索距离：

$\{\begin{array}{l}{X}_i=X\_axis+\text{rand}(·)\\ Y_i=Y\_axis+\text{rand}(·)\end{array}$ (17)

Step 3：因无法获得食物位置，先计算当前果蝇个体位置与原点的距离，后取距离的倒数作为果蝇个体的味道浓度判定值：

$Dis{t}_i=\sqrt{X_i{}^2+Y_i{}^2}$ (18)

$$ (19)

Step 4：将味道浓度判定值 $S_i$ 代入适应度函数，求出味道浓度 ${\text{Smell}}_i$ ：

(20)

Step 5：找出该果蝇群体中味道浓度值最佳的果蝇个体：

$\left[\text{bestSmell}\text{bestindex}\right]=\min \left({\text{Smell}}_i\right)$ (21)

Step 6：记录并保留最佳味道浓度值 $\text{bestSmell}$ 与其 $X$ 、 $Y$ 坐标，此时果蝇群体将向该位置飞去：

$$ (22)

Step 7：迭代寻优，重复执行Step 2~Step 6，并判断当前最佳味道浓度值是否优于前一迭代，并且判断是否达到最大迭代次数，若是停止运行。

3.2.3. 基于FOA算法的Elman神经网络预测模型

本文中，定义适应度函数为预测值与实际值的均方根误差：

$\text{RMSE}=\sqrt{\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left(P_i^r－P_i^f\right)}}{n}}$ (23)

式中， $n$ 为预测样本数量； $P_i^r$ 、 $P_i^f$ 分别为实际值和预测值。

Elman神经网络的相关参数由味道浓度判定值 $S_i$ 来表示，在每次迭代中，将获得的当前最佳味道浓度判定值 $S_i$ 代入Elman神经网络进行建模预测，并计算适应度值，重复执行Step 2~Step 6。当FOA算法到达最大迭代次数或终止条件时，迭代终止，得到Elman神经网络最优参数，将网络权值和阀值赋给Elman神经网络，进行训练及预测输出。

基于FOA-Elman的时空建模如图2所示，通过FOA-Elman神经网络估计获得NARX模型输出 $$ 与上文获得的空间基函数 ${\phi }_i\left(t\right)$ 进行时空综合，即可获得分布参数系统时空FOA-Elman模型，完整的时空FOA-Elman模型如下式所示：

$\{\begin{array}{l}\hat{y}\left(t\right)=\hat{F}\left(y\left(t-1\right)\cdots y\left(t-n_y\right),u\left(t-1\right)\cdots u\left(t-n_u\right)\right)\\ {\hat{y}}_n\left(x,t\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\phi }_i\left(x\right){\hat{y}}_i\left(t\right)}\end{array}$ (24)

图2. 时空FOA-Elman模型结构图

综合以上所述建模方法，分布参数系统的时空分解建模方法步骤总结如下：

Step 1：为分布参数系统施加激励，获得系统输出 ${\left\{y\left(x,t\right)\right\}}_{i=1,t=1}^{N,L}$ ，利用snapshots法得到系统空间基函数 ${\left\{{\varphi }_i\left(x\right)\right\}}_{i=1}^n$ 和时间系数 ${\left\{y\left(t\right)\right\}}_{t=1}^L$ 。

Step 2：在每个采样点处，对激励信号 $u\left(t\right)$ 和时间系数 $y\left(t\right)$ ，利用FOA-Elman进行模型辨识。

Step 3：系统重构，得到建模输出。

4. 仿真研究

4.1. 系统描述

对如下分布参数系统—催化过程 [17] 进行建模研究，验证建模方法的准确度。如图3所示，催化棒放置于一管式反应器中，物料A从一端进入经催化反应生成物料B从另一端排出。反应过程为放热反应，因而为保证反应器中的温度恒定，需要外界提供冷却介质。因此，控制目标为：控制冷却介质温度，使反应器在各空间位置和各时刻的温度都保持恒定。

图3. 催化反应过程

在一定条件下，该反应过程可以用如下偏微分方程和边界条件描述：

$\frac{\partial y\left(x,t\right)}{\partial t}=\frac{{\partial }^{2}y\left(x,t\right)}{\partial x^2}+{\beta }_T\left({\text{e}}^{-\frac{\gamma }{(1+y)}}-e^{-\gamma }\right)+{\beta }_u\left(b^T\left(x\right)u\left(t\right)-y\left(x,t\right)\right)$ (25)

边界条件为： $y\left(0,t\right)=0$ 、 $y\left(X,t\right)=0$ ，初始条件为： $y\left(x,0\right)=y_0\left(x\right)$ ，式中 $y\left(x,t\right)$ 、 $u\left(t\right)$ 、 $b\left(x\right)$ 、 ${\beta }_T$ 、 ${\beta }_u$ 、 $\gamma$ 、 $X$ 分别为反应器内温度、冷却介质温度、执行器空间分布函数、反应热量、导热系数、活化能量及反应器空间长度。

假设在管式反应器中等间隔的分布着4个控制器： $u\left(t\right)={\left[u_1\left(t\right),\cdots ,u_4\left(t\right)\right]}^T$ ，其空间分布函数为： $b\left(x\right)={\left[b_1\left(x\right),\cdots ,b_4\left(x\right)\right]}^T$ ，其中， $b_i\left(x\right)=H\left(x-\frac{\left(i-1\right)\text{π}}{4}\right)-H\left(x-\frac{i\text{π}}{4}\right)$ ， $H(\cdot )$ 为单位阶跃函数。

4.2. 时空FOA-Elman建模

为获得系统的snapshots，通过控制器对系统进行充分激励，选择激励信号为： $u_i\left(t\right)=1.1+5\sin \left(15t+\frac{i}{10}\right)\left(i=1,2,3,4\right)$ 。仿真过程主要参数设置如表1所示。

表1. 仿真参数设置

通过高阶有限差分法求解式(25)所示偏微分方程，获得系统真实响应值。在使用snapshots方法进行K-L时空分离时要求时间节点数要小于空间节点数。因此在本文中选择时间节点数L为100，空间节点

数N为120。经过有线差分法获得系统响应为： $y\left(x,t\right)={\left\{y\left(x_i,t_j\right)\right\}}_{i=1,j=1}^{120,100}$ ，系统响应如图4所示：

图4. 系统有限差分法求解结果

为了比较所取空间基函数个数n对建模精度的影响，定义如下性能指标：

$\text{RMSE}={\left(\frac{{\displaystyle \int {\displaystyle \sum e{\left(x,t\right)}^2\text{d}x}}}{{\displaystyle \int \text{d}x{\displaystyle \sum \Delta t}}}\right)}^{1/2}$ (26)

其中 $e\left(x,t\right)=y\left(x,t\right)-\hat{y}\left(x,t\right)$ 。

FOA-Elman神经网络模型中的模型阶数 $n_y,n_u$ 分别为3和4。FOA算法参数设置为多次运行最佳值，取Elman神经网络隐含层数量为7。在获得FOA-Elman模型之后，对其使用空间基函数进行时空综合，即可得到完整的时空FOA-Elman神经网络模型。图5为 $n=4$ 时的空间基函数，表2为取不同个数的空间基函数 $n$ 时FOA-Elman-PCA和Elman-PCA的RMSE对比。

图5. 空间基函数(n = 4)

表2. Elman-PCA与FOA-Elman-PCA的RMSE对比

从表2中可以看出，数据在经过PCA降维后，使用3个空间主导基函数，时空模型就可在整个空间上获得较高的建模精度；同时取得的主导空间基函数个数越多，建模精度越好，但是在n大于3后，建模精度的提升效果就不再明显。当所取主导空间基函数个数相同时，FOA-Elman-PCA的RMSE要小于Elman-PCA的RMSE。因此，在使用相同的主元数提取特征值，FOA-Elman-PCA具有更强的建模能力。因此，本文综合建模精度和复杂度，选取n = 3对系统进行建模仿真，其建模输出和建模误差分别如图6，图7所示。

为验证模型泛化能力，改变模型激励信号为： $u_i\left(t\right)=1.1+5\sin \left(16t+\frac{i}{10}\right)\left(i=1,2,3,4\right)$ ，经运算模型RMSE为0.0209。因此，本文所提出的建模方法有很好的建模精度和泛化能力。

图6. 时空FOA-Elman模型输出(n = 3)

图7. 时空FOA-Elman模型误差(n = 3)

5. 结论

本文给出了一种基于分布参数系统输入输出数据驱动的FOA-Elman时空分解建模方法。首先使用K-L分解对系统降维获得主导空间基函数，随后利用时空分解求得系统时间系数，并结合系统输入激励辨识出一个Elman神经网络模型，最后对系统进行模型重构，获得预测输出。本文研究方法不需要知道模型内部机理，仅仅依靠模型输入输出数据即可实现建模，同时具有建模方法简单、运算量小、精度高等特点，通过对催化反应过程的仿真表明，该方法对分布参数系统具有良好的建模能力和泛化能力。

文章引用

杨仁建,范瑛琦. 基于时空FOA-Elman的分布参数系统建模——时空建模
Time/Space Separation Based FOA-Elman Modeling for Non-Linear Distributed Parameter Processes—Spatial-Temporal Modeling[J]. 计算机科学与应用, 2019, 09(02): 328-338. https://doi.org/10.12677/CSA.2019.92038

参考文献