Advances in Applied Mathematics
Vol.
12
No.
12
(
2023
), Article ID:
77399
,
12
pages
10.12677/AAM.2023.1212500
蒙特卡罗方法在求解定积分中的应用研究
梁思敏,王玲芝*,李晨阳
西安邮电大学,自动化学院,陕西 西安
收稿日期:2023年6月5日;录用日期:2023年12月7日;发布日期:2023年12月18日

摘要
随着计算机和机器学习的发展,蒙特卡罗方法(Monte–Carlo,简称MC)逐渐成为用于近似计算的重要统计抽样理论。本文主要研究了蒙特卡罗方法在求解定积分中的应用,基于Matlab软件实现了一些定积分的蒙特卡罗方法求解。将蒙特卡罗方法求解得到的近似解与传统方法求解得到的准确值作对比,验证了蒙特卡罗方法求解定积分的可行性和优越性。同时,分析了蒙特卡罗方法求解定积分误差产生的原因,并提出了增加样本量、选择抽样方法、调整随机数生成函数等改进措施,以提高算法的计算精度。
关键词
蒙特卡罗方法,统计抽样原理,定积分

Research on the Application of Monte Carlo Method in Solving Definite Integrals
Simin Liang, Lingzhi Wang*, Chenyang Li
School of Automation, Xi’an University of Posts and Telecommunications, Xi’an Shaanxi
Received: Jun. 5th, 2023; accepted: Dec. 7th, 2023; published: Dec. 18th, 2023

ABSTRACT
With the development of computers and machine learning, Monte Carlo method (MC) has gradually become an important statistical sampling theory for approximate calculations. This paper mainly studies the application of Monte Carlo methods in solving definite integrals, and implements some Monte Carlo methods for solving definite integrals based on Matlab software. The comparison between the approximate solution obtained by Monte Carlo method and the accurate value obtained by traditional methods verifies the feasibility and superiority of Monte Carlo method for solving definite integrals. Meanwhile, the reasons for the error of Monte Carlo method in solving the definite integral are analyzed, and improvement measures such as increasing the sample size, selecting the sampling method, and adjusting the random number generation function are proposed to improve the calculation accuracy of the algorithm.
Keywords:Monte Carlo Method, Statistical Sampling Principle, Definite Integral

Copyright © 2023 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/


1. 引言
现代定积分理论发展至今已经非常成熟,涉及到包括实变函数、复变函数、测度论、泛函分析等多个分支领域。定积分不仅在数学领域中有广泛的应用,而且在物理、工程、金融等其他领域也有着重要的作用 [1] 。
求解定积分的传统方法有解析法和数值积分法。解析法是使用解析式直接求解定积分,例如对于多项式函数和三角函数等常见函数,都可以使用牛顿–莱布尼茨公式或基本积分公式来求解它们的定积分。然而,解析法仅适用于能够通过解析式求解的函数,对于复杂的函数可能无法使用解析法求解。数值积分法则是将定积分转化为数值积分,并通过一些数值方法来计算其近似值。常见的数值积分方法包括梯形法、辛普森法、龙贝格法等。这些方法可以处理复杂的函数,但计算精度可能会受到步长、维数等因素的影响。
传统的定积分求解方法发展至今已经非常完善,该方法能够求解得到定积分的精确结果,在一些要求高精度计算的应用中十分重要。对于需要保证计算精度的科学研究和实验,传统定积分求解方法是必不可少的。但是,当被积函数比较复杂时,传统方法往往无法求解或者计算精度会受到限制。于是引入蒙特卡罗方法,借助随机抽样求解。基于蒙特卡罗方法求解定积分,是使用随机抽样来模拟函数在积分区间上的取值,从而估算出定积分的值 [2] [3] 。蒙特卡罗法求解定积分相较于传统的求解方法,不受步长、维数等因素影响,适用于处理复杂的函数,并且具有较高的精度和通用性 [4] [5] [6] [7] [8] 。
本文采用蒙特卡罗方法计算简单定积分和复杂定积分,验证了蒙特卡罗方法求解的可行性和优越性。同时,分析了蒙特卡罗方法求解定积分产生误差的原因,并提出了一系列改进措施,以提高算法的计算精度。
2. 蒙特卡罗方法原理
蒙特卡罗方法的基本思想是将问题转化为一个随机过程,通过大量的随机抽样来估算随机变量的期望值,从而得到问题的近似解 [9] [10] [11] [12] 。具体来说,对于一个待求解的问题,可以构造一个随机变量,使得该随机变量的期望值就是所求问题的解。然后通过模拟实验来获取服从该随机变量的样本,利用这些样本来估算期望值,将期望值作为求解问题的近似解。
由基本思想可以推导出两种基于蒙特卡罗法求解定积分的方法,第一种是随机投点直接求解,本文称随机投点法;第二种是经过简单推导,将求解定积分的问题转化为求解期望问题来求近似解,本文称期望法。
2.1. 随机投点法原理
随机投点法 [11] 的原理图如图1所示。假设求解形如 的定积分,则根据定积分的几何性质,定积分的近似解为f(x)曲线与下方x轴围成的面积,即图1中灰色阴影部分的面积。
使用蒙特卡罗方法(随机投点)求解定积分,选取一个面积确定的矩形,必须包含所求函数的积分区间,假设其面积为S。然后向这个区域(图中正方形区域)随机投点,落在函数f(x)下方的点接受(如图中绿色的点),其余的点拒绝(如图中红色的点),统计绿色点的数量占所有点的数量的比例为R,则可以估算出定积分 的近似值为S * R。
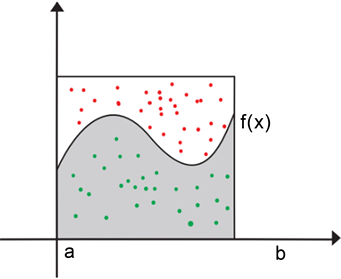
Figure 1. Principle of point casting method
图1. 投点法原理
2.2. 期望法求解原理
另一种求解思路称蒙特卡罗期望法。如图2所示,假设求解形如 的定积分,f(x)为被积函数且在被积区间内连续。则根据定积分的几何性质,所求积分T近似等于图2中阴影部分的面积。

Figure 2. Principle of expectancy method for solving
图2. 期望法求解原理
f(x)是随机变量x的函数,则它的数学期望如式(1)所示。
(1)
若x在[a, b]区间内均匀分布,抽取n个随机样本 (满足均匀分布)。则有:
(2)
采样数n越多,估计值越接近准确值。然而大多数情况下x在[a, b]上并不是均匀分布,就会导致上述方法存在较大的误差。
假设g(x)是某个概率密度分布函数,且满足 。则可进行如下推导:
(3)
令 ,式(3)可转化为:
(4)
根据式(1),式(4)可继续推导得出:
(5)
则式(5)就是蒙特卡罗期望法计算定积分的一般形式。
此时,求解定积分的问题就转化成了如何从g(x)中进行采样 [5] [6] [7] 。为了验证方法的可行性,本文将同时采用均匀分布、正态分布和Beta分布来求解定积分(本文分别称算法2、算法3和算法4,统称期望法),并分别将计算结果与传统方法进行比较,验证求解结果的准确性。
3. 求解定积分的实现
3.1. 简单定积分的实现
由于复杂的定积分无法求出准确的解析解,为了验证蒙特卡罗方法对定积分求解结果的可靠性,先选取简单的定积分算例,分别使用投点法和期望法进行求解,并与传统方法的解析解进行对比。
算例1:求解
1) 解析法计算过程
2) 蒙特卡罗方法计算过程
基于模拟实验中产生随机序列所服从分布的不同,选择不同分布进行模拟实验。考虑到随机数产生位置的随机性,为使实验数据更加准确,选择多次进行模拟,实验结果如表1所示。
Table 1. Calculation results of Example 1
表1. 算例1计算结果
注:算法1:随机投点法计算;算法2:采用期望法–均匀分布函数求解;算法3:采用期望法–正态分布函数求解;算法4:采用期望法–Beta分布函数求解(后面文中算法含义均与此相同)。
算例2:求解
1) 解析法求解过程
2) 蒙特卡罗方法计算结果如表2所示。
Table 2. Calculation results of Example 2
表2. 算例2计算结果
注:表中数据单位均为*104。
由算例1和算例2可以看出,每个算法与使用解析法求解的结果,误差均在可允许的误差范围内,证明了蒙特卡罗方法求解定积分的可行性。
3.2. 复杂定积分的实现
传统定积分的解法虽然可以得到积分结果的精确值,然而当被积函数复杂时,形如 的被积函数(其中 ),无法得到原函数的解析解。只能通过数值积分法来计算近似解,而数值积分法的计算精确度受到步长的影响。此时,使用蒙特卡罗方法求解定积分,可以克服上述局限性。
算例3:求解
数值积分法求解时,利用Matlab的函数库的trapz函数来实现,求解结果为: 。
蒙特卡罗模拟法求解结果如表3所示。
Table 3. Calculation results of Example 3
表3. 算例3计算结果
注:a表中数据单位均为*108。
算例4:求解
数值积分法求解结果为 ,蒙特卡罗模拟法求解结果如下表4所示。
Table 4. Calculation results of Example 4
表4. 算例4计算结果
注:a表中数据单位均为*1013。
从表3和表4的计算结果可知,使用蒙特卡罗方法求解算例3,计算结果与使用数值积分法的误差不大,但是算例4数值积分法的计算结果与蒙特卡罗方法的计算结果出现较大误差。由于数值积分法的计算结果会受步长的影响,我们合理推测使用蒙特卡罗方法求解得到的结果更接近实际结果的近似值。由于算法1的计算过程中,数据有较大误差,舍弃算法1的计算值,将算法2、算法3、算法4的计算结果均值,作为最终计算结果为:
4. 模拟结果分析
前面的求解结果证明了使用蒙特卡罗方法求解定积分的可行性。但是,由于随机抽样所得到的样本点,并不完全代表被积函数在积分区间内的整体情况,导致估算值与真实值之间存在偏差。因此,蒙特卡罗方法的求解结果通常会存在一定的误差。为了提高蒙特卡罗方法求解定积分的精确度,接下来分析可能影响精确度,带来误差的原因,并提出提高精确度的优化建议。
4.1. 采样次数不同的误差分析
由于蒙特卡罗方法是一种基于随机抽样来求解计算结果的方法,考虑到随机数产生位置的不均匀性,采样的次数N可能会对模拟结果产生影响。本文将采用不同的N值,来分析采样次数对模拟结果带来的影响。为了更准确的分析计算结果,先选取已知精确解的算例1进行分析,结果如表5所示。由于单次实验数据并不准确,不同的N值将选取六次实验取平均值作为参考。
Table 5. Calculation results for Example 1 with different N values
表5. 算例1不同N值时的计算结果
为了更直观地观测N值不同的计算结果,将各算法不同N计算结果的均值做误差直观图如图3所示。
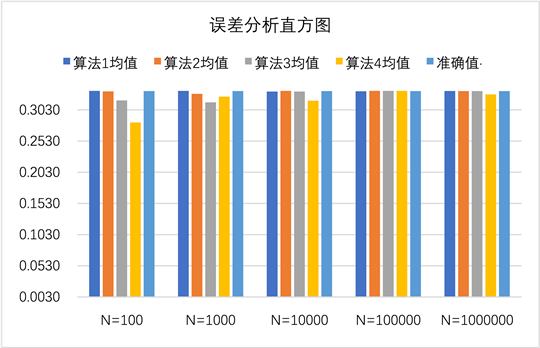
Figure 3. Histograms with different N values in Example 1
图3. 算例1中N值不同时的直方图
1) 当采样次数N较小(N < 1000)时,算法3和算法4的计算结果准确度不如算法1和算法2。
2) 当采样次数N较大(N ≥ 1000)时,算法1、算法2和算法3的计算准确度都与准确值一致。但是当N = 10,000和N = 1,000,000时,算法4的计算结果精度略次于其他三种算法,可能是由于Beta分布函数的概率密度函数分布曲线所造成的,具体将在后面进行详细分析。
将上述分析简单算例的思路引入到分析不同N对复杂定积分计算结果的影响中,验证简单定积分的结论是否适用于复杂定积分的求解。选取算例4进行验证,算例的求解结果如表6所示。
Table 6. Calculation results for Example 4 with different N values
表6. 算例4不同N值时的计算结果
注:表中数据单位均为1013。
同样为了更直观的观测N值不同的计算结果,将各算法取不同N值计算结果的均值做误差直方图如图4所示。
对图4进行如下分析:如果被积函数比较复杂,当采样次数N = 100时,各算法相较于准确值均有较大误差;当采样次数N ≥ 1000时,各算法的误差均在可观范围内。但当N = 100000时,算法1反而有较大误差。
由上述两个分析结果可知,采样次数对蒙特卡罗方法求解定积分计算结果的精确度的确有影响。对于两个算例,合适的采样次数并不相同。总之,随着采样次数N的增加,计算结果的精确度会增加。
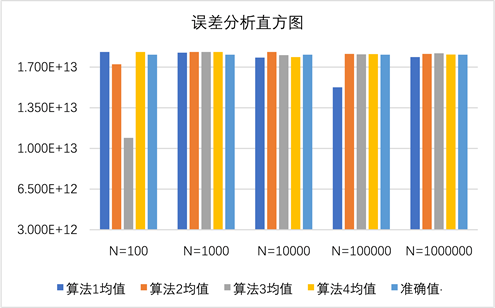
Figure 4. Error histogram of Example 4
图4. 算例4的误差直方图
在实际应用中,往往无法事先确定合适的采样次数,在合适的采样次数未知时,考虑根据经验值,选定一个采样次数,多此进行模拟实验求取平均值来提高精确度。
求解定积分时,可以通过不断增加采样次数,来提高精确度。但是注意在具体操作时,需要观察计算结果的稳定性和收敛速度。当计算结果有较大的跳跃性时,可以适当增加采样次数;而当计算结果趋于稳定时,考虑算法的优化或者更换随机数发生器,找到一个相对合适的算法及采样次数,以提高计算结果的精确度。
4.2. 模拟次数不同的误差分析
采用蒙特卡罗方法求解定积分问题时,样本数量的选择是一个关键因素。若采样次数过少,可能出现所有采样点均不在所需范围内的情况,导致计算结果有较大偏差。在这种情况下,尝试增加模拟试验次数并将结果求取平均值,来提高计算结果的精确度。图5和图6分别是对算例1做6次模拟实验和12次模拟实验的数据表。
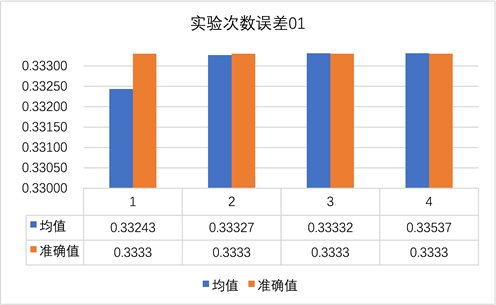
Figure 5. Error histogram of six simulation experiments in Example 1
图5. 算例1六次模拟实验的误差直方图

Figure 6. Error histogram of twelve simulation experiments in Example 1
图6. 算例1十二次模拟实验的误差直方图
由图5和图6对比可以看出,当只做6次模拟实验时,计算结果已经非常接近准确值,但是算法1和算法4只有2位有效数字与准确值相同,算法2有3位有效数字与准确值相同,算法3有4位有效数字与准确值相同。而12次模拟实验时,算法2和算法3均与准确值有4位相同有效数字,算法1和算法4均与准确值有3位相同有效数字。
由此可见,增加模拟试验次数,并取多次计算结果的平均值作为最终求解的近似值,可以有效地减小抽样误差,提高计算精度。
4.3. 概率密度函数不同的误差分析
考虑到不同的分布函数具有不同的意义和分布曲线,采样范围的变化导致采样点的分布不均匀 [7] ,可能会对计算结果产生影响。
为了更好地评估不同方法在求解定积分问题时的精确度和可靠性,引用样本标准偏差(表达式如式(6)所示)分析比对不同算法的计算数据结果的离散程度,进而判断使用不同的随机分布对模拟结果的准确度是否具有显著性影响。
(6)
如表7所示,为了评估算法的适用性和分析计算中数据结果的离散程度,将前面所有算例的计算结果取平均值,再使用式(6)计算出本文中出现算例的计算结果标准偏差 [7] ,来衡量算法计算结果的离散度。标准偏差过大,说明算法的计算结果离散度较大,可能会影响计算结果精确度。
当使用期望法的算法2、算法3、算法4求解定积分时,算法3使用正态分布进行采样,由于正态分布的曲线在采样区间具有无论参数的选择,基本都是中间高两边低的分布特点,所以在各算例的计算过程中,方差都较小;而算法4的Beta分布在参数选取不同时,概率密度函数的曲线分布有较大差异,最合适的采样次数也不同,求解过程中要不断调整参数来提高其精准度。所以在图3中,当N取N = 1,000,000算法4的精确度会下降。因为算法3和算法4的概率密度函数曲线有着较大差异,在生成随机数时,随机数产生的区域不同,对蒙特卡罗方法求解定积分的计算精确度影响也不同。
算法2在算例1中具有较好的服从性,算法3在算例3中具有较好的服从性,算法4在算例2和算例4中具有较好的服从性。由此可见,使用不同的概率密度函数对蒙特卡罗方法求解定积分结果的精确度确有影响。在实际应用时,可以根据需要求解的问题进行概率密度函数的选择以及参数的调节。
Table 7. Comparison of discrepancy of algorithms
表7. 算法的离散度比较
此外,为了评估各算法的计算效率,还需要比较不同算法在相同条件下的计算时间。在求解过程中注意到,不同的方法,实现相同的定积分求解,所需的算法时间是不同的,算法时间如图7所示。
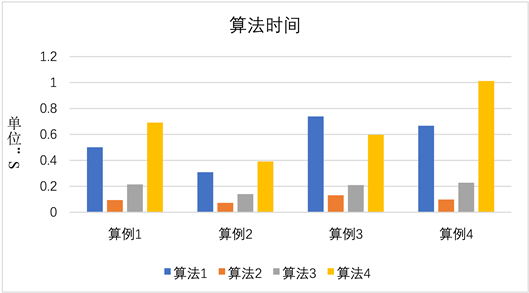
Figure 7. The computing time of algorithms
图7. 算法的计算时间
从图7可以看到,在使用蒙特卡罗方法求解定积分时,不同的算法所需时间存在一定差异。综合考虑算法的计算时间和计算结果的离散度,选择正态分布的概率密度函数可以更好的平衡计算时间和结果精确度的需求。
5. 优化建议
尽管蒙特卡罗方法在求解复杂定积分时具有很大的优势,但基于随机抽样的方法也会带来各种误差。目前本文已经分析了采样次数、模拟次数、概率密度函数选取等因素对结果精确度的影响,为了减少这些误差,提高计算的精确度,建议采取以下几个优化措施:
1) 在计算定积分时,传统的投点法无论是对于简单函数还是复杂函数都有一些缺陷,例如计算精度不高和实验数据分散度大等问题。因此,在选择蒙特卡罗方法时,采用优化的期望法可以有效提高计算结果的精度。相比传统方法,期望法在计算随机变量的数学期望时考虑了各个样本的概率权重,从而改善了计算结果的分散和不确定性,并且能够适应各种不同的概率密度函数情况。因此,采用优化的期望法可以在蒙特卡罗方法求解定积分问题中提高计算的准确性和稳定性。通过增加采样次数和重复模拟次数,提高计算精度。
2) 在使用蒙特卡罗方法求解定积分时,选择合适的概率密度函数是十分重要的。不同的概率密度函数会影响到计算结果的准确性、计算时间以及数据分散度等方面。因此,在选择概率密度函数时需要充分考虑这些因素,并根据具体问题的特点和要求进行合理选择,以提高计算效率和结果的准确性。
3) 使用蒙特卡罗方法求解定积分时,提高随机抽取的样本数量、提高模拟实验次数,可以明显提高计算结果准确性。但是,在提高样本数量和实验次数的同时,也会带来计算时间的耗费,需要考虑时间和精度之间的平衡点。如果所需计算的误差范围较小或所求解的函数比较复杂,可以适当提高样本数和采样次数。如果计算时间不受限制,则可以尝试增大样本数和采样次数来达到更高的精确度。
6. 结论
本文采用蒙特卡罗方法实现了对简单定积分和复杂定积分的求解。通过蒙特卡罗方法计算简单定积分算例的结果与精确值比较,验证了算法的可行性。当被积函数复杂时,与传统定积分的求解方法相比,蒙特卡罗方法求解定积分具有实现程序简单、计算结果精度高等显著优点。为了减小误差,可以通过增加样本容量、选择合适的概率密度函数、增加重复模拟次数等方法,提高模拟方法计算结果的精确度。
基金项目
国家自然科学基金项目(61903298)。
文章引用
梁思敏,王玲芝,李晨阳. 蒙特卡罗方法在求解定积分中的应用研究
Research on the Application of Monte Carlo Method in Solving Definite Integrals[J]. 应用数学进展, 2023, 12(12): 5093-5104. https://doi.org/10.12677/AAM.2023.1212500
参考文献
- 1. 杜玉平. 定积分的常用计算方法探析[J]. 湖南工业职业技术学院学报, 2018, 18(4): 27-30.
- 2. 梅淳惠. 逾渗模型的蒙特卡罗模拟[D]: [硕士学位论文]. 南京: 南京邮电大学, 2016.
- 3. 张朝俊. 计算金融学中的拟蒙特卡洛方法: 光滑化和重要性抽样[D]: [博士学位论文]. 北京: 清华大学, 2019.
- 4. 杨少华. Monte Carlo方法在定积分近似计算中的应用[J]. 长春大学学报, 2012, 22(2): 185-187.
- 5. 杨筱珊. 蒙特卡罗方法在定积分近似计算中的应用[J]. 安顺师专学报(自然科学版), 1998(2): 34-40.
- 6. 张艳. 利用蒙特卡罗方法求解数值积分[J]. 高等数学研究, 2023, 26(1): 44-46+61.
- 7. 车金星. 蒙特卡洛计算方法及其在定积分求解中的应用[J]. 考试周刊, 2011(88): 71-72.
- 8. Tamang, N. and Sun, Y. (2023) Application of the Dynamic Monte Carlo Method to Pedestrian Evacuation Dynamics. Applied Mathematics and Computation, 445, 127876. https://doi.org/10.1016/j.amc.2023.127876
- 9. Yu, S.Y., Wu, W.H. and Naess, A. (2023) Extreme Value Predic-tion with Modified Enhanced Monte Carlo Method Based on Tail Index Correction. Journal of Sea Research, 192, 102354. https://doi.org/10.1016/j.seares.2023.102354
- 10. 王涛. 期权定价的蒙特卡罗模拟方差缩减技术研究及应用[D]: [硕士学位论文]. 成都: 西南财经大学, 2010.
- 11. 柴中林, 银俊成. 蒙特卡罗方法计算定积分的进一步讨论[J]. 应用数学与计算数学学报, 2008(1): 125-128.
- 12. 黄慧敏. 两类期权定价模型的蒙特卡罗模拟[D]: [硕士学位论文]. 北京: 华北电力大学(北京), 2022.
NOTES
*通讯作者。
