Creative Education Studies
Vol.
07
No.
06
(
2019
), Article ID:
33473
,
6
pages
10.12677/CES.2019.76136
Research on the Teaching of Frequently-Used Discrete Distribution Cases
Xiaoyan Liu, Mo Li, Cuiling Ma
School of Basic Sciences for Aviation, NAU, Yantai Shandong

Received: Nov. 28th, 2019; accepted: Dec. 10th, 2019; published: Dec. 17th, 2019

ABSTRACT
In the classroom teaching, we should not only pay attention to the discussion and deduction of the basic theory, but also pay attention to the introduction and application of the theoretical part. In the classroom teaching, the explanation of practical application cases can not only effectively stimulate students’ enthusiasm for learning, but also help them to understand the key points of relevant knowledge.
Keywords:Central Limit Theorem, Teaching Case

中心极限定理案例教学探索
刘晓燕,李 沫,马翠玲
海军航空大学航空基础学院,山东 烟台

收稿日期:2019年11月28日;录用日期:2019年12月10日;发布日期:2019年12月17日

摘 要
课堂教学中不但要注重基本理论的论述及推导,更应注重理论部分的引入和应用展示。在课堂教学中通过对实际应用案例的讲解,不但能够有效激发学生的学习热情,更能帮助他们进一步理解相关知识要点。
关键词 :中心极限定理,案例教学

Copyright © 2019 by author(s) and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
本文主要针对中心极限定理这一概率统计 [1] [2] [3] 中的基本知识点展开案例教学的探索,以“北非登陆战”这一经典战例为整节课的线索,针对抽象的定理,利用多媒体生动形象的特点,借助图形化抽象为直观,改变学生对偏理论性内容的抵触心理,同时,将相似的知识点进行比较区分,并辅以典型例题的详细讲解。总体思路:
首先,从登陆作战的第一步“航渡”出发提出问题;
其次,通过对问题的分析,引出De Moivre-Laplace中心极限定理,并利用定理解决前面提出的问题;
再次,借助登陆作战的第二步“抢滩上陆”对De Moivre-Laplace中心极限定理的条件进行改进,即独立同分布的中心极限定理,并利用定理求解该实例;
最后,对本次课的内容做一下小结,并对登陆作战的第三步“发展进攻”留一道课后思考题。
2. 问题的提出
所谓登陆作战,是指军队对据守海岛、海岸之敌的渡海进攻行动,又称两栖作战。目的是夺取敌占岛屿、海岸等重要目标,或在敌岸建立进攻出发地域,为尔后的作战行动创造条件。战争中的“登陆作战”作为由海洋到陆地的重要过渡,是解决未来海上局部战争的主要作战模式之一。一次完整的“登陆作战”主要由以下三个步骤构成(图1):
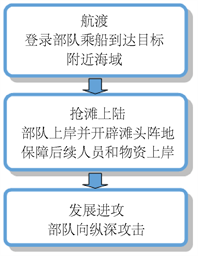
Figure 1. Process of landing operation
图1. 登陆作战流程
第二次世界大战的北非登陆战中,美国巴顿将军利用科学预测,率领舰队冲破风浪横渡大西洋来到北非战场并实现了成功登陆。对此次“登陆作战”的第一步——航渡,收集并分析相应的数据可合理简化得以下数学模型。
引例巴顿舰队的舰艇在横渡大西洋的途中会遭受约90,000次独立波浪冲击,每遭受一次冲击横摇角超过某一危险阈值的概率约为1/3。若舰艇能承受约30,400次以下的这种危险的冲击,则巴顿舰队的舰艇能成功抵达登陆地点的概率是多少?
分析:对于舰队中的舰艇,设在第i次波浪冲击中
则 间相互独立且同0~1分布。所求概率为: 。
类似和式的分布问题在现实中是非常常见的,其相应的概率要借助De Moivre-Laplace中心极限定理来分析求解。
3. De Moivre-Laplace中心极限定理
De Moivre-Laplace中心极限定理 设 是一个独立同分布的随机变量序列,且
,,则对任意一个x, ,总有
分析:
① 条件中,随机变量 相互独立,且 ,即 也可认为是独立同0~1分布的。故
;
② 利用MATLAB画出参数n较大,p取不同值时,二项分布的图像(图2),它们都呈现中间高,两端低,且左右近似对称状,即类似正态分布概率密度函数特有的钟形图像。
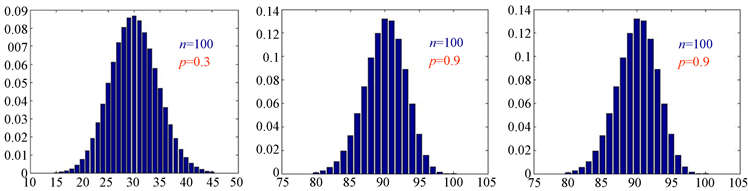
Figure 2. Comparison of binomial distribution figures
图2. 二项分布图形比较
数学问题基本上都是抽象的,因此在理解上往往具有一定的难度,尤其De Moivre-Laplace中心极限定理中还涉及概率的极限问题,学生理解起来会更为吃力。因此,在此处运用数学软件的绘图功能,并用多媒体课件进行比较展示,使学生可以对该定理有更为直观的认识,从而帮助他们进一步理解和记忆该定理。
由此也可进一步总结简化定理的结论。定理说明:
① 当n较大时, ;
② 当n较大时, 。
为了避免与相似的结论混淆,此处可以插入对前面学习过的“二项分布在一定条件下可由Piosson分布近似”内容的复习,进行相似知识点的比较:若 ,则
① 当n较大,p较小, 适中时,有: ;
② 当n较大,p不较小,或 并不适中时, 。
利用定理求解引例:
引例 解:设舰艇受危险冲击的总次数为 ,则 。故
答:舰队能成功抵达的概率约为0.9977。
学生往往被动地接受知识,学习具有一定的盲目性,满足于会做题即可。如果不能很好解决学生深层次的学习需求,那么整个学习过程将缺乏一种主动的导向和目标,最终将累积导致丧失学习兴趣和动力。学生学习最大的困惑在于不知道为什么学,不知道学了之后有什么用,因此在课程设计和讲授过程中,应致力于解决这个问题。通过对教学内容及过程的精心设计,除了完成基本知识的转移和传递,更重要的是进一步教会学生如何应用所学知识。从实际问题上升到理论,而后从理论又回归到实际,通过这样一个往复的过程,完成学生意识的螺旋式上升,达到真正掌握知识并会运用知识的目的。
4. 独立同分布的中心极限定理
针对“独立同分布的中心极限定理”,采取类似的设计思路:提出问题–分析问题–解决问题。首先,延续“登陆作战”的流程,第二步——抢滩上陆,即以舰载火炮及空中火力为火力支持,为部队上岸并开辟滩头阵地,保障后续人员和物资上岸提供有利条件。构建以下数学模型。
例舰载火炮现对敌人的某防御工事进行炮击,在每次炮击中炮弹命中的颗数是相互独立且同分布的,其数学期望为2,标准差为1.5。若防御工事被击中170发炮弹即告被摧毁,求在100次炮击中,敌方防御工事被摧毁的概率。
分析:若设 为第i次炮击炮弹命中的颗数,则所求概率为:
但在此处 虽然独立同分布,但却不服从0~1分布,De Moivre-Laplace中心极限定理不再适用,考虑使用另一中心极限定理。
独立同分布的中心极限定理设 是一个独立同分布的随机变量序列,且 ,,则对任意一个x, ,总有
独立同分布的中心极限定理的结论与De Moivre-Laplace中心极限定理类似,给出的都是相应概率的极限;但与De Moivre-Laplace中心极限定理相比,独立同分布的中心极限定理去掉了 的条件,即不需要考虑随机变量 的分布情况,只需了解了 的期望和方差,就可得到其和的近似分布。
在一般情况下,很难了解到随机变量序列 中各个随机变量的分布情况,更不用说求出n个随机变量之和的分布函数,由此更体现出了独立同分布的中心极限的优越性。即当n充分大时,可以利用正态分布对n个独立同分布的随机变量之和作理论分析或作实际计算。
利用定理求解例题:
例 解:设 为第i次炮击炮弹命中的颗数。由已知 独立同分布,且 ,。故
答:敌工事被摧毁的概率约为0.9772。
当然,在实际问题中,随机变量序列 中各个随机变量的同分布性往往也较难保证,但只要它们之间相互独立,就可用另一中心极限定理——Lyapunov定理来进行讨论。由于课程时间限制,这一定理可放至课后引导感兴趣的学生进行自学。
5. 小结与思考
中心极限定理(central limit theorem)是概率论中讨论随机变量序列部分和分布如何能近似于正态分布的一类定理的总称。在客观实际中,有许多随机变量是由大量的相互独立的随机因素的综合影响所形成的,而其中每一个个别因素在总的影响中所起到的作用都是微小的,这种随机变量往往近似地服从正态分布。中心极限定理就是从数学上证明了这一现象。
在数学史上最早出现的中心极限定理是De Moivre-Laplace中心极限。这个定理的最初版是法国数学家De Moivre在1733年发表的论文中,使用正态分布去估计大量抛掷硬币出现正面次数的分布时提出的,并由另一位法国数学家Laplace在1812年在其著作中进行了扩展——指出二项分布可用正态分布逼近。但同De Moivre一样,Laplace的发现在当时并未引起很大反响,直到十九世纪末中心极限定理的重要性才被世人所知。1901年,俄国数学家Lyapunov用更一般的随机变量定义中心极限定理,并在理论上进行了精确的证明。中心极限定理是概率论的重要内容,也是数理统计学的基石之一,其理论成果也比较完美。长期以来,对于中心极限定理的研究所形成的概率论分析方法影响着概率论的发展,同时新的中心极限理论问题也在实际中不断产生。如今,中心极限定理更是被许多人认为是概率论中的首席定理。而在本次课中重点学习的De Moivre-Laplace中心极限定理与独立同分布的中心极限定理打破了一般课本中的讲授顺序,采取了由“特殊”到“一般”的分析过程,而这一讲授设计顺序也更符合中心极限定理在数学史中的发展历程。
对于“登陆作战”的第三步——发展进攻,留一思考题。
思考题 部队抢滩上陆后向内陆进发过程中,需用汽车进行兵员的运送,汽车最大载重量为5吨,超重运行会危害其上战士的安全。若战士的平均体重为
本次课在教学设计过程中,始终贯彻“向实战聚焦,向部队靠拢”的思想,坚持“必须够用”的原则,尽可能地设计与军事作战和部队生活相关的实例,并将其融入教学内容,以引起学生学习兴趣。从而实现在认知上,使学生掌握两个中心极限定理,并能用其解决实际问题,达到基本知识传授的目的;在能力方面,以经典登陆作战的战例为基础,培养学生提出问题,分析问题和解决问题的能力,即实现基本技能的培养;从情感上,改变学生对数学枯燥无味,神秘难懂的印象,让他们看到课堂上所学的知识可以直接应用于登陆作战的分析中去,充分调动他们学习的主动性,实现创新思维的启迪。
文章引用
刘晓燕,李 沫,马翠玲. 中心极限定理案例教学探索
Research on the Teaching of Frequently-Used Discrete Distribution Cases[J]. 创新教育研究, 2019, 07(06): 801-806. https://doi.org/10.12677/CES.2019.76136
参考文献
- 1. 浙江大学数学系. 概率论与数理统计[M]. 第四版. 北京: 高等教育出版社, 2008.
- 2. 同济大学应用数学系. 概率统计简明教程[M]. 北京: 高等教育出版社, 2003.
- 3. Ross, S.M. 概率论基础教程[M]. 北京: 人民邮电出版社, 2010.