从四面体到N维单形的棱切球心、热尔岗点、奈格尔点及其坐标公式 Edge-Tangent’s Sphere Center, Gergonne Point, Nagel Point and Their Coordinate Formula from Tetrahedron to N-Simplex

doi:10.12677/PM.2021.111019

Pure Mathematics
Vol. 11 No. 01 ( 2021 ), Article ID: 40127 , 12 pages
10.12677/PM.2021.111019

从四面体到N维单形的棱切球心、热尔岗点、奈格尔点及其坐标公式

李兴源

●How to Cite this Article

广州一智通供应链管理有限公司，广东广州

收稿日期：2020年12月21日；录用日期：2021年1月22日；发布日期：2021年1月29日

摘要

四面体存在棱切球的充要条件是该四面体的三组对棱之和相等。对于存在棱切球的四面体，本文给出其棱切球心、热尔岗点、奈格尔点的坐标公式，并将这三者的坐标公式推广至存在棱切超球面的n维单形。

关键词

四面体，棱切球，热尔岗点，奈格尔点，n维单形

Edge-Tangent’s Sphere Center, Gergonne Point, Nagel Point and Their Coordinate Formula from Tetrahedron to N-Simplex

Xingyuan Li

Guangzhou 1ziton Supply Chain Management Co., Ltd., Guangzhou Guangdong

Received: Dec. 21^st, 2020; accepted: Jan. 22^nd, 2021; published: Jan. 29^th, 2021

ABSTRACT

The sufficient and necessary condition for the tetrahedron to have an edge-tangent’s sphere is that the sum of the three groups of opposite sides is equal in the tetrahedron. For a tetrahedron with an edge-tangent’s sphere, the coordinate formula of the edge-tangent’s sphere center, Gergonne Point and Nagel Point is given in this paper, and the coordinate formulas of these three points are extended to n-simplex with an edge-tangent’s hypersphere.

Keywords:Tetrahedron, Edge-Tangent’s Sphere, Gergonne Point, Nagel Point, n-Simplex

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

1. 引言

如图1所示，若四面体ABCD存在棱切球，各棱上的切点分别为 $M_{A B}$ 、 $M_{A C}$ 、 $M_{A D}$ 、 $M_{B C}$ 、 $M_{B D}$ 、 $M_{C D}$ 。本文约定O为坐标原点，A、B、C、D四点的坐标分别为 $(x_{1}, y_{1}, z_{1})$ 、 $(x_{2}, y_{2}, z_{2})$ 、 $(x_{3}, y_{3}, z_{3})$ 、 $(x_{4}, y_{4}, z_{4})$ ；设

$A M_{A B} = A M_{A C} = A M_{A D} = a$ , $B M_{A B} = B M_{B C} = B M_{B D} = b$ ,

$C M_{A C} = C M_{B C} = C M_{C D} = c$ , $D M_{A D} = D M_{B D} = D M_{C D} = d$ [1] .

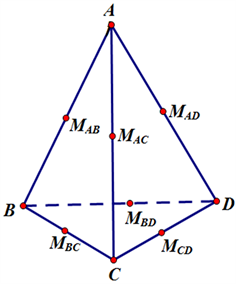
Figure 1. The tangent points on edge-tangent’s sphere of the tetrahedron

图1. 四面体棱切球上的各切点

2. 棱切球心的坐标公式

2.1. 四面体的棱切球心

若四面体ABCD的三组对棱之和相等即存在棱切球，则四面体ABCD的棱切球心坐标为

$(\frac{F_{1}}{(a + b) (a + c) (a + d) F}, \frac{F_{2}}{(a + b) (a + c) (a + d) F}, \frac{F_{3}}{(a + b) (a + c) (a + d) F})$ 。其中，

$F_{1} = | \begin{matrix} (\vec{O B} - \vec{O A}) (a \cdot \vec{O B} + b \cdot \vec{O A}) & (a + b) (y_{2} - y_{1}) & (a + b) (z_{2} - z_{1}) \\ (\vec{O C} - \vec{O A}) (a \cdot \vec{O C} + c \cdot \vec{O A}) & (a + c) (y_{3} - y_{1}) & (a + c) (z_{3} - z_{1}) \\ (\vec{O D} - \vec{O A}) (a \cdot \vec{O D} + d \cdot \vec{O A}) & (a + d) (y_{4} - y_{1}) & (a + d) (z_{4} - z_{1}) \end{matrix} |$ ,

$F_{2} = | \begin{matrix} (a + b) (x_{2} - x_{1}) & (\vec{O B} - \vec{O A}) (a \cdot \vec{O B} + b \cdot \vec{O A}) & (a + b) (z_{2} - z_{1}) \\ (a + c) (x_{3} - x_{1}) & (\vec{O C} - \vec{O A}) (a \cdot \vec{O C} + c \cdot \vec{O A}) & (a + c) (z_{3} - z_{1}) \\ (a + d) (x_{4} - x_{1}) & (\vec{O D} - \vec{O A}) (a \cdot \vec{O D} + d \cdot \vec{O A}) & (a + d) (z_{4} - z_{1}) \end{matrix} |$ ,

$F_{3} = | \begin{matrix} (a + b) (x_{2} - x_{1}) & (a + b) (y_{2} - y_{1}) & (\vec{O B} - \vec{O A}) (a \cdot \vec{O B} + b \cdot \vec{O A}) \\ (a + c) (x_{3} - x_{1}) & (a + c) (y_{3} - y_{1}) & (\vec{O C} - \vec{O A}) (a \cdot \vec{O C} + c \cdot \vec{O A}) \\ (a + d) (x_{4} - x_{1}) & (a + d) (y_{4} - y_{1}) & (\vec{O D} - \vec{O A}) (a \cdot \vec{O D} + d \cdot \vec{O A}) \end{matrix} |$ ,

$F = | \begin{matrix} 1 & x_{1} & y_{1} & z_{1} \\ 1 & x_{2} & y_{2} & z_{2} \\ 1 & x_{3} & y_{3} & z_{3} \\ 1 & x_{4} & y_{4} & z_{4} \end{matrix} |$ .

证明：设四面体ABCD的棱切球心为P，由棱切球的性质可知

$P M_{A B} ⊥ A B$ , $P M_{A C} ⊥ A C$ , $P M_{A D} ⊥ A D$ [2] .

再设平面 $π_{1}$ 、 $π_{2}$ 、 $π_{3}$ 分别过 $M_{A B}$ 、 $M_{A C}$ 、 $M_{A D}$ 且分别垂直于AB、AC、AD，则四面体ABCD的棱切球心P即为 $π_{1}$ 、 $π_{2}$ 、 $π_{3}$ 这三个平面的交点。

由定比分点公式可得 $M_{A B}$ 、 $M_{A C}$ 、 $M_{A D}$ 三点的坐标分别为 $(\frac{a x_{2} + b x_{1}}{a + b}, \frac{a y_{2} + b y_{1}}{a + b}, \frac{a z_{2} + b z_{1}}{a + b})$ 、 $(\frac{a x_{3} + c x_{1}}{a + c}, \frac{a y_{3} + c y_{1}}{a + c}, \frac{a z_{3} + c z_{1}}{a + c})$ 、 $(\frac{a x_{4} + d x_{1}}{a + d}, \frac{a y_{4} + d y_{1}}{a + d}, \frac{a z_{4} + d z_{1}}{a + d})$ 。

则平面 $π_{1}$ 的方程为：

$(x_{2} - x_{1}) (x - \frac{a x_{2} + b x_{1}}{a + b}) + (y_{2} - y_{1}) (y - \frac{a y_{2} + b y_{1}}{a + b}) + (z_{2} - z_{1}) (z - \frac{a z_{2} + b z_{1}}{a + b}) = 0$ .

整理可得：

$\begin{array}{l} (a + b) [(x_{2} - x_{1}) x + (y_{2} - y_{1}) y + (z_{2} - z_{1}) z] \\ = (x_{2} - x_{1}) (a x_{2} + b x_{1}) + (y_{2} - y_{1}) (a y_{2} + b y_{1}) + (z_{2} - z_{1}) (a z_{2} + b z_{1}) \\ = (\vec{O B} - \vec{O A}) (a \cdot \vec{O B} + b \cdot \vec{O A}) \end{array}$ . ①

同理平面 $π_{2}$ 、 $π_{3}$ 的方程分别为：

$(a + c) [(x_{3} - x_{1}) x + (y_{3} - y_{1}) y + (z_{3} - z_{1}) z] = (\vec{O C} - \vec{O A}) (a \cdot \vec{O C} + c \cdot \vec{O A})$ . ②

$(a + d) [(x_{4} - x_{1}) x + (y_{4} - y_{1}) y + (z_{4} - z_{1}) z] = (\vec{O D} - \vec{O A}) (a \cdot \vec{O D} + d \cdot \vec{O A})$ . ③

联立① ② ③所组成的线性方程组，并运用克拉姆法则解得 [3]：

$\begin{matrix} x = \frac{| \begin{matrix} (\vec{O B} - \vec{O A}) (a \cdot \vec{O B} + b \cdot \vec{O A}) & (a + b) (y_{2} - y_{1}) & (a + b) (z_{2} - z_{1}) \\ (\vec{O C} - \vec{O A}) (a \cdot \vec{O C} + c \cdot \vec{O A}) & (a + c) (y_{3} - y_{1}) & (a + c) (z_{3} - z_{1}) \\ (\vec{O D} - \vec{O A}) (a \cdot \vec{O D} + d \cdot \vec{O A}) & (a + d) (y_{4} - y_{1}) & (a + d) (z_{4} - z_{1}) \end{matrix} |}{(a + b) (a + c) (a + d) | \begin{matrix} x_{2} - x_{1} & y_{2} - y_{1} & z_{2} - z_{1} \\ x_{3} - x_{1} & y_{3} - y_{1} & z_{3} - z_{1} \\ x_{4} - x_{1} & y_{4} - y_{1} & z_{4} - z_{1} \end{matrix} |} \\ = \frac{| \begin{matrix} (\vec{O B} - \vec{O A}) (a \cdot \vec{O B} + b \cdot \vec{O A}) & (a + b) (y_{2} - y_{1}) & (a + b) (z_{2} - z_{1}) \\ (\vec{O C} - \vec{O A}) (a \cdot \vec{O C} + c \cdot \vec{O A}) & (a + c) (y_{3} - y_{1}) & (a + c) (z_{3} - z_{1}) \\ (\vec{O D} - \vec{O A}) (a \cdot \vec{O D} + d \cdot \vec{O A}) & (a + d) (y_{4} - y_{1}) & (a + d) (z_{4} - z_{1}) \end{matrix} |}{(a + b) (a + c) (a + d) | \begin{matrix} 1 & x_{1} & y_{1} & z_{1} \\ 1 & x_{2} & y_{2} & z_{2} \\ 1 & x_{3} & y_{3} & z_{3} \\ 1 & x_{4} & y_{4} & z_{4} \end{matrix} |} \end{matrix}$ ,

$\begin{matrix} y = \frac{| \begin{matrix} (a + b) (x_{2} - x_{1}) & (\vec{O B} - \vec{O A}) (a \cdot \vec{O B} + b \cdot \vec{O A}) & (a + b) (z_{2} - z_{1}) \\ (a + c) (x_{3} - x_{1}) & (\vec{O C} - \vec{O A}) (a \cdot \vec{O C} + c \cdot \vec{O A}) & (a + c) (z_{3} - z_{1}) \\ (a + d) (x_{4} - x_{1}) & (\vec{O D} - \vec{O A}) (a \cdot \vec{O D} + d \cdot \vec{O A}) & (a + d) (z_{4} - z_{1}) \end{matrix} |}{(a + b) (a + c) (a + d) | \begin{matrix} x_{2} - x_{1} & y_{2} - y_{1} & z_{2} - z_{1} \\ x_{3} - x_{1} & y_{3} - y_{1} & z_{3} - z_{1} \\ x_{4} - x_{1} & y_{4} - y_{1} & z_{4} - z_{1} \end{matrix} |} \\ = \frac{| \begin{matrix} (a + b) (x_{2} - x_{1}) & (\vec{O B} - \vec{O A}) (a \cdot \vec{O B} + b \cdot \vec{O A}) & (a + b) (z_{2} - z_{1}) \\ (a + c) (x_{3} - x_{1}) & (\vec{O C} - \vec{O A}) (a \cdot \vec{O C} + c \cdot \vec{O A}) & (a + c) (z_{3} - z_{1}) \\ (a + d) (x_{4} - x_{1}) & (\vec{O D} - \vec{O A}) (a \cdot \vec{O D} + d \cdot \vec{O A}) & (a + d) (z_{4} - z_{1}) \end{matrix} |}{(a + b) (a + c) (a + d) | \begin{matrix} 1 & x_{1} & y_{1} & z_{1} \\ 1 & x_{2} & y_{2} & z_{2} \\ 1 & x_{3} & y_{3} & z_{3} \\ 1 & x_{4} & y_{4} & z_{4} \end{matrix} |} \end{matrix}$ ,

$z = \frac{| \begin{matrix} (a + b) (x_{2} - x_{1}) & (a + b) (y_{2} - y_{1}) & (\vec{O B} - \vec{O A}) (a \cdot \vec{O B} + b \cdot \vec{O A}) \\ (a + c) (x_{3} - x_{1}) & (a + c) (y_{3} - y_{1}) & (\vec{O C} - \vec{O A}) (a \cdot \vec{O C} + c \cdot \vec{O A}) \\ (a + d) (x_{4} - x_{1}) & (a + d) (y_{4} - y_{1}) & (\vec{O D} - \vec{O A}) (a \cdot \vec{O D} + d \cdot \vec{O A}) \end{matrix} |}{(a + b) (a + c) (a + d) | \begin{matrix} x_{2} - x_{1} & y_{2} - y_{1} & z_{2} - z_{1} \\ x_{3} - x_{1} & y_{3} - y_{1} & z_{3} - z_{1} \\ x_{4} - x_{1} & y_{4} - y_{1} & z_{4} - z_{1} \end{matrix} |}$

$= \frac{| \begin{matrix} (a + b) (x_{2} - x_{1}) & (a + b) (y_{2} - y_{1}) & (\vec{O B} - \vec{O A}) (a \cdot \vec{O B} + b \cdot \vec{O A}) \\ (a + c) (x_{3} - x_{1}) & (a + c) (y_{3} - y_{1}) & (\vec{O C} - \vec{O A}) (a \cdot \vec{O C} + c \cdot \vec{O A}) \\ (a + d) (x_{4} - x_{1}) & (a + d) (y_{4} - y_{1}) & (\vec{O D} - \vec{O A}) (a \cdot \vec{O D} + d \cdot \vec{O A}) \end{matrix} |}{(a + b) (a + c) (a + d) | \begin{matrix} 1 & x_{1} & y_{1} & z_{1} \\ 1 & x_{2} & y_{2} & z_{2} \\ 1 & x_{3} & y_{3} & z_{3} \\ 1 & x_{4} & y_{4} & z_{4} \end{matrix} |}$ .

2.2. N维单形的棱切球心

由文献 [4] 可知，n维单形 $A_{0} A_{1} \dots A_{n}$ 存在棱切超球的充要条件是其各棱长满足：

$A_{i} A_{j} = a_{i} + a_{j}$ , ( $0 \leq i \neq j \leq n$ , $a_{i}, a_{j} \in R^{+}$ ).

设 $A_{i}$ 的坐标为 $(x_{i, 1}, x_{i, 2}, \dots, x_{i, n})$ ，参照前面的方法可以求出n维单形 $A_{0} A_{1} \dots A_{n}$ 的棱切超球球心坐标为 $(\frac{F_{1}}{F \prod_{i = 1}^{n} (a_{0} + a_{i})}, \frac{F_{2}}{F \prod_{i = 1}^{n} (a_{0} + a_{i})}, \dots, \frac{F_{n}}{F \prod_{i = 1}^{n} (a_{0} + a_{i})})$ 。其中，

$F_{1} = | \begin{matrix} (\vec{O A_{1}} - \vec{O A_{0}}) (a_{0} \cdot \vec{O A_{1}} + a_{1} \cdot \vec{O A_{0}}) & (a_{0} + a_{1}) (x_{1, 2} - x_{0, 2}) & \dots & (a_{0} + a_{1}) (x_{1, n} - x_{0, n}) \\ (\vec{O A_{2}} - \vec{O A_{0}}) (a_{0} \cdot \vec{O A_{2}} + a_{2} \cdot \vec{O A_{0}}) & (a_{0} + a_{2}) (x_{2, 2} - x_{0, 2}) & \dots & (a_{0} + a_{2}) (x_{2, n} - x_{0, n}) \\ ⋮ & ⋮ & ⋱ & ⋮ \\ (\vec{O A_{n}} - \vec{O A_{0}}) (a_{0} \cdot \vec{O A_{n}} + a_{n} \cdot \vec{O A_{0}}) & (a_{0} + a_{n}) (x_{n, 2} - x_{0, 2}) & \dots & (a_{0} + a_{n}) (x_{n, n} - x_{0, n}) \end{matrix} |$ ,

$F_{2} = | \begin{matrix} (a_{0} + a_{1}) (x_{1, 1} - x_{0, 1}) & (\vec{O A_{1}} - \vec{O A_{0}}) (a_{0} \cdot \vec{O A_{1}} + a_{1} \cdot \vec{O A_{0}}) & (a_{0} + a_{1}) (x_{1, 3} - x_{0, 3}) & \dots & (a_{0} + a_{1}) (x_{1, n} - x_{0, n}) \\ (a_{0} + a_{2}) (x_{2, 1} - x_{0, 1}) & (\vec{O A_{2}} - \vec{O A_{0}}) (a_{0} \cdot \vec{O A_{2}} + a_{2} \cdot \vec{O A_{0}}) & (a_{0} + a_{2}) (x_{2, 3} - x_{0, 3}) & \dots & (a_{0} + a_{2}) (x_{2, n} - x_{0, n}) \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ \\ (a_{0} + a_{n}) (x_{n, 1} - x_{0, 1}) & (\vec{O A_{n}} - \vec{O A_{0}}) (a_{0} \cdot \vec{O A_{n}} + a_{n} \cdot \vec{O A_{0}}) & (a_{0} + a_{n}) (x_{n, 3} - x_{0, 3}) & \dots & (a_{0} + a_{n}) (x_{n, n} - x_{0, n}) \end{matrix} |$ , $\dots$ ,

$F_{n} = | \begin{matrix} (a_{0} + a_{1}) (x_{1, 1} - x_{0, 1}) & \dots & (a_{0} + a_{1}) (x_{1, n - 1} - x_{0, n - 1}) & (\vec{O A_{1}} - \vec{O A_{0}}) (a_{0} \cdot \vec{O A_{1}} + a_{1} \cdot \vec{O A_{0}}) \\ (a_{0} + a_{2}) (x_{2, 1} - x_{0, 1}) & \dots & (a_{0} + a_{2}) (x_{2, n - 1} - x_{0, n - 1}) & (\vec{O A_{2}} - \vec{O A_{0}}) (a_{0} \cdot \vec{O A_{2}} + a_{2} \cdot \vec{O A_{0}}) \\ ⋮ & ⋱ & ⋮ & ⋮ \\ (a_{0} + a_{n}) (x_{n, 1} - x_{0, 1}) & \dots & (a_{0} + a_{n}) (x_{n, n - 1} - x_{0, n - 1}) & (\vec{O A_{n}} - \vec{O A_{0}}) (a_{0} \cdot \vec{O A_{n}} + a_{n} \cdot \vec{O A_{0}}) \end{matrix} |$ ,

$F = | \begin{matrix} 1 & x_{0, 1} & \dots & x_{0, n} \\ 1 & x_{1, 1} & \dots & x_{1, n} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 1 & x_{n, 1} & \dots & x_{n, n} \end{matrix} |$ .

3. 热尔岗(Gergonne)点的坐标公式

对于图1所示的四面体ABCD，设在A、B、C、D四点所对之面上的热尔岗点分别为 $G_{1}$ 、 $G_{2}$ 、 $G_{3}$ 、 $G_{4}$ 。

3.1. 三角形的热尔岗(Gergonne)点

如图2所示，对于图1所示四面体ABCD中的三角形ABC：A、B、C分别与三角形ABC的内切圆在对边上的切点 $M_{B C}$ 、 $M_{A C}$ 、 $M_{A B}$ 的连线 $A M_{B C}$ 、 $B M_{A C}$ 、 $C M_{A B}$ 三线相交的热尔岗点为 $G_{4}$ 。由前面引言可知

$A B = a + b$ , $B C = b + c$ , $A C = a + c$ .

则 $G_{4}$ 的坐标为

$\vec{O G_{4}} = \frac{\frac{1}{a} \cdot \vec{O A} + \frac{1}{b} \cdot \vec{O B} + \frac{1}{c} \cdot \vec{O C}}{\frac{1}{a} + \frac{1}{b} + \frac{1}{c}} = \frac{b c \cdot \vec{O A} + a c \cdot \vec{O B} + a b \cdot \vec{O C}}{b c + a c + a b}$ .

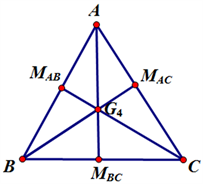
Figure 2. Gergonne points in triangle (Gergonne point)

图2. 三角形的切心(热尔岗点)

证明：由定比分点公式，有

$\vec{O M_{B C}} = \frac{b \cdot \vec{O C} + c \cdot \vec{O B}}{b + c}$ , $\vec{O M_{A C}} = \frac{a \cdot \vec{O C} + c \cdot \vec{O A}}{a + c}$ , $\vec{O M_{A B}} = \frac{a \cdot \vec{O B} + b \cdot \vec{O A}}{a + b}$ .

设

$\frac{A G_{4}}{G_{4} M_{B C}} = λ_{1}$ , $\frac{B G_{4}}{G_{4} M_{A C}} = λ_{2}$ , $\frac{C G_{4}}{G_{4} M_{A B}} = λ_{3}$ ,

则 $\vec{O G_{4}}$ 有以下三种表示：

$\vec{O G_{4}} = \frac{\vec{O A} + λ_{1} \cdot \vec{O M_{B C}}}{1 + λ_{1}} = \frac{(b + c) \cdot \vec{O A} + c λ_{1} \cdot \vec{O B} + b λ_{1} \cdot \vec{O C}}{(b + c) (1 + λ_{1})}$ ,

$\vec{O G_{4}} = \frac{\vec{O B} + λ_{2} \cdot \vec{O M_{A C}}}{1 + λ_{2}} = \frac{(a + c) \cdot \vec{O B} + a λ_{2} \cdot \vec{O C} + c λ_{2} \cdot \vec{O A}}{(a + c) (1 + λ_{2})}$ ,

$\vec{O G_{4}} = \frac{\vec{O C} + λ_{3} \cdot \vec{O M_{A B}}}{1 + λ_{3}} = \frac{(a + b) \cdot \vec{O C} + b λ_{3} \cdot \vec{O A} + a λ_{3} \cdot \vec{O B}}{(a + b) (1 + λ_{3})}$ .

对上面三式的 $\vec{O A}$ 、 $\vec{O B}$ 、 $\vec{O C}$ 的系数分别进行比较，可得

$\frac{1}{1 + λ_{1}} = \frac{c λ_{2}}{(a + c) (1 + λ_{2})} = \frac{b λ_{3}}{(a + b) (1 + λ_{3})}$ , ①

$\frac{1}{1 + λ_{2}} = \frac{a λ_{3}}{(a + b) (1 + λ_{3})} = \frac{c λ_{1}}{(b + c) (1 + λ_{1})}$ , ②

$\frac{1}{1 + λ_{3}} = \frac{b λ_{1}}{(b + c) (1 + λ_{1})} = \frac{a λ_{2}}{(a + c) (1 + λ_{2})}$ , ③

把上面三式相乘并整理可得

$λ_{1} λ_{2} λ_{3} = \frac{(a + c) (a + b) (b + c)}{a b c}$ ;

再分别把① ② ③中的任意两式相乘并整理可得

$λ_{1} λ_{2} = \frac{(a + c) (b + c)}{c^{2}}$ , $λ_{1} λ_{3} = \frac{(a + b) (b + c)}{b^{2}}$ , $λ_{2} λ_{3} = \frac{(a + b) (a + c)}{a^{2}}$ .

解得

$λ_{1} = \frac{a (b + c)}{b c}$ , $λ_{2} = \frac{b (a + c)}{a c}$ , $λ_{3} = \frac{c (a + b)}{a b}$ .

因此

3.2. 四面体的热尔岗(Gergonne)点

对于图1所示的四面体ABCD，由文献 [5] 可知， $A G_{1}$ 、 $B G_{2}$ 、 $C G_{3}$ 、 $D G_{4}$ 这四条直线在四面体ABCD内交于一点，设该点为G即四面体ABCD的热尔岗(Gergonne)点。

由前面引言可知

$A B = a + b$ , $B C = b + c$ , $A C = a + c$ , $A D = a + d$ , $B D = b + d$ , $C D = c + d$ .

则G的坐标为

$\vec{O G} = \frac{\frac{1}{a} \cdot \vec{O A} + \frac{1}{b} \cdot \vec{O B} + \frac{1}{c} \cdot \vec{O C} + \frac{1}{d} \cdot \vec{O D}}{\frac{1}{a} + \frac{1}{b} + \frac{1}{c} + \frac{1}{d}} = \frac{b c d \cdot \vec{O A} + a c d \cdot \vec{O B} + a b d \cdot \vec{O C} + a b c \cdot \vec{O D}}{b c d + a c d + a b d + a b c}$ .

证明：由于

$\vec{O G_{4}} = \frac{\frac{1}{a} \cdot \vec{O A} + \frac{1}{b} \cdot \vec{O B} + \frac{1}{c} \cdot \vec{O C}}{\frac{1}{a} + \frac{1}{b} + \frac{1}{c}}$ ;

同理

$\vec{O G_{1}} = \frac{\frac{1}{b} \cdot \vec{O B} + \frac{1}{c} \cdot \vec{O C} + \frac{1}{d} \cdot \vec{O D}}{\frac{1}{b} + \frac{1}{c} + \frac{1}{d}}$ ,

$\vec{O G_{2}} = \frac{\frac{1}{a} \cdot \vec{O A} + \frac{1}{c} \cdot \vec{O C} + \frac{1}{d} \cdot \vec{O D}}{\frac{1}{a} + \frac{1}{c} + \frac{1}{d}}$ ,

$\vec{O G_{3}} = \frac{\frac{1}{a} \cdot \vec{O A} + \frac{1}{b} \cdot \vec{O B} + \frac{1}{d} \cdot \vec{O D}}{\frac{1}{a} + \frac{1}{b} + \frac{1}{d}}$ .

因为点G为 $A G_{1}$ 、 $B G_{2}$ 、 $C G_{3}$ 、 $D G_{4}$ 这四条直线的交点，设

$\frac{A G}{G G_{1}} = λ_{1}$ , $\frac{B G}{G G_{2}} = λ_{2}$ , $\frac{C G}{G G_{3}} = λ_{3}$ , $\frac{D G}{G G_{4}} = λ_{4}$ .

则 $\vec{O G}$ 有以下四种表示：

$\vec{O G} = \frac{\vec{O A} + λ_{1} \cdot \vec{O G_{1}}}{1 + λ_{1}} = \frac{(\frac{1}{b} + \frac{1}{c} + \frac{1}{d}) \cdot \vec{O A} + λ_{1} \cdot (\frac{1}{b} \cdot \vec{O B} + \frac{1}{c} \cdot \vec{O C} + \frac{1}{d} \cdot \vec{O D})}{(\frac{1}{b} + \frac{1}{c} + \frac{1}{d}) (1 + λ_{1})}$ ,

$\vec{O G} = \frac{\vec{O B} + λ_{2} \cdot \vec{O G_{2}}}{1 + λ_{2}} = \frac{(\frac{1}{a} + \frac{1}{c} + \frac{1}{d}) \cdot \vec{O B} + λ_{2} \cdot (\frac{1}{a} \cdot \vec{O A} + \frac{1}{c} \cdot \vec{O C} + \frac{1}{d} \cdot \vec{O D})}{(\frac{1}{a} + \frac{1}{c} + \frac{1}{d}) (1 + λ_{2})}$ ,

$\vec{O G} = \frac{\vec{O C} + λ_{3} \cdot \vec{O G_{3}}}{1 + λ_{3}} = \frac{(\frac{1}{a} + \frac{1}{b} + \frac{1}{d}) \cdot \vec{O C} + λ_{3} \cdot (\frac{1}{a} \cdot \vec{O A} + \frac{1}{b} \cdot \vec{O B} + \frac{1}{d} \cdot \vec{O D})}{(\frac{1}{a} + \frac{1}{b} + \frac{1}{d}) (1 + λ_{3})}$ ,

$\vec{O G} = \frac{\vec{O D} + λ_{4} \cdot \vec{O G_{4}}}{1 + λ_{4}} = \frac{(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}) \cdot \vec{O D} + λ_{4} \cdot (\frac{1}{a} \cdot \vec{O A} + \frac{1}{b} \cdot \vec{O B} + \frac{1}{c} \cdot \vec{O C})}{(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}) (1 + λ_{4})}$ .

对上面四式的 $\vec{O A}$ 、 $\vec{O B}$ 、 $\vec{O C}$ 、 $\vec{O D}$ 的系数分别进行比较，可得

$\frac{1}{1 + λ_{1}} = \frac{\frac{1}{a} λ_{2}}{(\frac{1}{a} + \frac{1}{c} + \frac{1}{d}) (1 + λ_{2})} = \frac{\frac{1}{a} λ_{3}}{(\frac{1}{a} + \frac{1}{b} + \frac{1}{d}) (1 + λ_{3})} = \frac{\frac{1}{a} λ_{4}}{(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}) (1 + λ_{4})}$ ,

$\frac{1}{1 + λ_{2}} = \frac{\frac{1}{b} λ_{3}}{(\frac{1}{a} + \frac{1}{b} + \frac{1}{d}) (1 + λ_{3})} = \frac{\frac{1}{b} λ_{4}}{(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}) (1 + λ_{4})} = \frac{\frac{1}{b} λ_{1}}{(\frac{1}{b} + \frac{1}{c} + \frac{1}{d}) (1 + λ_{1})}$ ,

$\frac{1}{1 + λ_{3}} = \frac{\frac{1}{c} λ_{4}}{(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}) (1 + λ_{4})} = \frac{\frac{1}{c} λ_{1}}{(\frac{1}{b} + \frac{1}{c} + \frac{1}{d}) (1 + λ_{1})} = \frac{\frac{1}{c} λ_{2}}{(\frac{1}{a} + \frac{1}{c} + \frac{1}{d}) (1 + λ_{2})}$ ,

$\frac{1}{1 + λ_{4}} = \frac{\frac{1}{d} λ_{1}}{(\frac{1}{b} + \frac{1}{c} + \frac{1}{d}) (1 + λ_{1})} = \frac{\frac{1}{d} λ_{2}}{(\frac{1}{a} + \frac{1}{c} + \frac{1}{d}) (1 + λ_{2})} = \frac{\frac{1}{d} λ_{3}}{(\frac{1}{a} + \frac{1}{b} + \frac{1}{d}) (1 + λ_{3})}$ .

对上面四式联立可得

$\begin{matrix} \frac{a}{1 + λ_{1}} = \frac{b}{1 + λ_{2}} = \frac{c}{1 + λ_{3}} = \frac{d}{1 + λ_{4}} \\ = \frac{λ_{1}}{(\frac{1}{b} + \frac{1}{c} + \frac{1}{d}) (1 + λ_{1})} = \frac{λ_{2}}{(\frac{1}{a} + \frac{1}{c} + \frac{1}{d}) (1 + λ_{2})} \\ = \frac{λ_{3}}{(\frac{1}{a} + \frac{1}{b} + \frac{1}{d}) (1 + λ_{3})} = \frac{λ_{4}}{(\frac{1}{a} + \frac{1}{b} + \frac{1}{c}) (1 + λ_{4})} \end{matrix}$ .

解得

$λ_{1} = a (\frac{1}{b} + \frac{1}{c} + \frac{1}{d})$ , $λ_{2} = b (\frac{1}{a} + \frac{1}{c} + \frac{1}{d})$ , $λ_{3} = c (\frac{1}{a} + \frac{1}{b} + \frac{1}{d})$ , $λ_{4} = d (\frac{1}{a} + \frac{1}{b} + \frac{1}{c})$ .

因此

3.3. N维单形的热尔岗(Gergonne)点

若n维单形 $A_{0} A_{1} \dots A_{n}$ 存在棱切超球，且各棱长满足：

$A_{i} A_{j} = a_{i} + a_{j}$ , ( $0 \leq i \neq j \leq n$ , $a_{i}, a_{j} \in R^{+}$ ).

设 $A_{0}$ 、 $A_{1}$ 、 $\dots$ 、 $A_{n}$ 各点在其所对之面上的热尔岗点分别为 $G_{0}$ 、 $G_{1}$ 、 $\dots$ 、 $G_{n}$ 。则诸直线 $A_{0} G_{0}$ 、 $A_{1} G_{1}$ 、 $\dots$ 、 $A_{n} G_{n}$ 在n维单形 $A_{0} A_{1} \dots A_{n}$ 内交于一点，设该点为G即n维单形 $A_{0} A_{1} \dots A_{n}$ 的热尔岗点，其坐标为

$\vec{O G} = \frac{\sum_{i = 0}^{n} \frac{1}{a_{i}} \cdot \vec{O A_{i}}}{\sum_{i = 0}^{n} \frac{1}{a_{i}}}$ .

证明：前面已经证明了当 $n = 3$ 时命题成立。假设当 $n = k$ 时命题同样成立 $(k \geq 3, k \in Z)$ ，现使用数学归纳法证明当 $n = k + 1$ 时命题依然成立。由归纳假设可得

$\vec{O G_{i}} = \frac{\sum_{j = 0}^{k + 1} \frac{1}{a_{j}} \cdot \vec{O A_{j}} - \frac{1}{a_{i}} \cdot \vec{O A_{i}}}{\sum_{j = 0}^{k + 1} \frac{1}{a_{j}} - \frac{1}{a_{i}}}$ , $0 \leq i \leq k + 1$ .

若点G为 $A_{0} G_{0}$ 、 $A_{1} G_{1}$ 、 $\dots$ 、 $A_{k + 1} G_{k + 1}$ 这 $k + 2$ 条直线的交点，设

$\frac{A_{i} G}{G G_{i}} = λ_{i}$ .

则

$\vec{O G} = \frac{\vec{O A_{i}} + λ_{i} \cdot \vec{O G_{i}}}{1 + λ_{i}} = \frac{(\sum_{j = 0}^{k + 1} \frac{1}{a_{j}} - \frac{1}{a_{i}}) \cdot \vec{O A_{i}} + λ_{i} \cdot (\sum_{j = 0}^{k + 1} \frac{1}{a_{j}} \cdot \vec{O A_{j}} - \frac{1}{a_{i}} \cdot \vec{O A_{i}})}{(\sum_{j = 0}^{k + 1} \frac{1}{a_{j}} - \frac{1}{a_{i}}) (1 + λ_{i})}$ .

对上式中的i分别取0到 $k + 1$ 之间的各个整数值，并对 $\vec{O A_{i}}$ 的系数分别进行比较，可得

$\frac{1}{1 + λ_{i}} = \frac{λ_{j} \cdot \frac{1}{a_{i}}}{(\sum_{i = 0}^{k + 1} \frac{1}{a_{i}} - \frac{1}{a_{j}}) (1 + λ_{j})}$ , $(0 \leq i \neq j \leq k + 1)$ .

对上式中的i、j取遍各种符合条件的取值并联立可得

$\frac{a_{i}}{1 + λ_{i}} = \frac{λ_{i}}{(\sum_{j = 0}^{k + 1} \frac{1}{a_{j}} - \frac{1}{a_{i}}) (1 + λ_{i})}$ .

解得

$λ_{i} = a_{i} (\sum_{j = 0}^{k + 1} \frac{1}{a_{j}} - \frac{1}{a_{i}})$ .

因此

$\vec{O G} = \frac{\sum_{i = 0}^{k + 1} \frac{1}{a_{i}} \cdot \vec{O A_{i}}}{\sum_{i = 0}^{k + 1} \frac{1}{a_{i}}}$ .

故 $n \geq 3$ 时命题均成立。

4. 奈格尔(Nagel)点的坐标公式

由文献 [6] 可知，若四面体ABCD存在内棱切球，则四面体ABCD在各棱的临棱区均存在侧棱切球。如图3所示，对于同时存在内棱切球和6个侧棱切球的四面体ABCD，其6个侧棱切球在各棱上的切点分别为 ${M^{'}}_{A B}$ 、 ${M^{'}}_{A C}$ 、 ${M^{'}}_{A D}$ 、 ${M^{'}}_{B C}$ 、 ${M^{'}}_{B D}$ 、 ${M^{'}}_{C D}$ 。

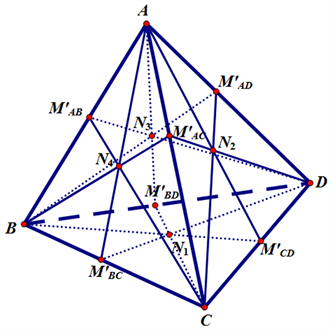
Figure 3. The tangent points of six chamfered edge- tangent’s sphere on each edge of the tetrahedron

图3. 四面体6个侧棱切球在各棱上的切点

4.1. 三角形的奈格尔(Nagel)点

对于图3所示的四面体ABCD，根据侧棱切球的性质可知：直线 $B {M^{'}}_{C D}$ 、 $C {M^{'}}_{B D}$ 、 $D {M^{'}}_{B C}$ 的交点 $N_{1}$ 为三角形BCD的奈格尔点；直线 $A {M^{'}}_{C D}$ 、 $C {M^{'}}_{A D}$ 、 $D {M^{'}}_{A C}$ 的交点 $N_{2}$ 为三角形ACD的奈格尔点；直线 $A {M^{'}}_{B D}$ 、 $B {M^{'}}_{A D}$ 、 $D {M^{'}}_{A B}$ 的交点 $N_{3}$ 为三角形ABD的奈格尔点；直线 $A {M^{'}}_{B C}$ 、 $B {M^{'}}_{A C}$ 、 $C {M^{'}}_{A B}$ 的交点 $N_{4}$ 为三角形ABC的奈格尔点。根据三角形等距共轭点的性质，设

$B {M^{'}}_{A B} = C {M^{'}}_{A C} = D {M^{'}}_{A D} = a$ , $A {M^{'}}_{A B} = C {M^{'}}_{B C} = D {M^{'}}_{B D} = b$ ,

$A {M^{'}}_{A C} = B {M^{'}}_{B C} = D {M^{'}}_{C D} = c$ , $A {M^{'}}_{A D} = B {M^{'}}_{B D} = C {M^{'}}_{C D} = d$ .

则 $N_{1}$ 、 $N_{2}$ 、 $N_{3}$ 、 $N_{4}$ 的坐标分别为

$\vec{O N_{1}} = \frac{b \cdot \vec{O B} + c \cdot \vec{O C} + d \cdot \vec{O D}}{b + c + d}$ ,

$\vec{O N_{2}} = \frac{a \cdot \vec{O A} + c \cdot \vec{O C} + d \cdot \vec{O D}}{a + c + d}$ ,

$\vec{O N_{3}} = \frac{a \cdot \vec{O A} + b \cdot \vec{O B} + d \cdot \vec{O D}}{a + b + d}$ ,

$\vec{O N_{4}} = \frac{a \cdot \vec{O A} + b \cdot \vec{O B} + c \cdot \vec{O C}}{a + b + c}$ [7] .

4.2. 四面体的奈格尔(Nagel)点

对于图3所示的四面体ABCD， $A N_{1}$ 、 $B N_{2}$ 、 $C N_{3}$ 、 $D N_{4}$ 这四条直线在四面体ABCD内交于一点，设该点为N即四面体ABCD的奈格尔(Nagel)点。又

$A B = a + b$ , $B C = b + c$ , $A C = a + c$ , $A D = a + d$ , $B D = b + d$ , $C D = c + d$ .

则N的坐标为

$\vec{O N} = \frac{a \cdot \vec{O A} + b \cdot \vec{O B} + c \cdot \vec{O C} + d \cdot \vec{O D}}{a + b + c + d}$ .

证明从略，可参考前面四面体热尔岗点坐标的计算方法。

4.3. N维单形的奈格尔(Nagel)点

若n维单形 $A_{0} A_{1} \dots A_{n}$ 存在棱切超球，且各棱长满足：

$A_{i} A_{j} = a_{i} + a_{j}$ , ( $0 \leq i \neq j \leq n$ , $a_{i}, a_{j} \in R^{+}$ ).

设 $A_{0}$ 、 $A_{1}$ 、 $\dots$ 、 $A_{n}$ 各点在其所对之面上的奈格尔点分别为 $N_{0}$ 、 $N_{1}$ 、 $\dots$ 、 $N_{n}$ 。则诸直线 $A_{0} N_{0}$ 、 $A_{1} N_{1}$ 、 $\dots$ 、 $A_{n} N_{n}$ 在n维单形 $A_{0} A_{1} \dots A_{n}$ 内交于一点，设该点为N即n维单形 $A_{0} A_{1} \dots A_{n}$ 的热尔岗点，其坐标为

$\vec{O N} = \frac{\sum_{i = 0}^{n} a_{i} \cdot \vec{O A_{i}}}{\sum_{i = 0}^{n} a_{i}}$ .

证明从略，同理可参考前面对n使用数学归纳法进行证明。

文章引用

李兴源. 从四面体到N维单形的棱切球心、热尔岗点、奈格尔点及其坐标公式
Edge-Tangent’s Sphere Center, Gergonne Point, Nagel Point and Their Coordinate Formula from Tetrahedron to N-Simplex[J]. 理论数学, 2021, 11(01): 131-142. https://doi.org/10.12677/PM.2021.111019

参考文献

1. 贺斌. 四面体存在棱切球的一个充要条件[J]. 中学数学月刊, 1998(3): 46.

2. 翁玉中. 关于多面体的棱切球的存在性[J]. 中学数学月刊, 1997(8): 14-16.

3. 赵艳. 克拉姆法则证明的新方法与几何解释[J]. 数学教学研究, 2012, 31(3): 53-54.

4. 林祖成. n维单形的棱切超球[J]. 数学实践与认识, 1995(4): 90-93.

5. 曾建国. 四面体的约尔刚(Gergonne)点[J]. 数学通讯, 2009, 12(2): 31-32.

6. 曾建国. 四面体的侧棱切球与奈格尔(Nagel)点[J]. 中学数学教学, 2010(4): 58-60.

7. 邓胜. 三角形特殊点的一般坐标公式[J]. 数学通讯, 1998(8): 24-26.

期刊菜单